Many readers will be familiar with the puzzle illustrated in Fig. 1, in which the triangle ABC is isosceles and angles a, b, c are given. If a, b, c are integers when expressed in degrees then it might appear, at first sight, that so must angle θ be. But this is not the case. The reader will quickly find that θ is not accessible by simple ‘angle chasing’. By this I mean marking in the

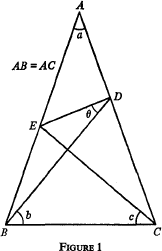
angles obtained by making the angles in any triangle sum to 180° and by making the exterior angle of any triangle equal the sum of the interior opposites. The following question arises: Given a, b, c can angle θ be obtained by pure geometry? My conjecture is that the answer is yes in those cases when angles a, b, c and θ are all multiples of the same angle. However, I am far from proving this, and have obtained geometrical derivations only for a limited number of cases, as will be seen.