No CrossRef data available.
Article contents
The accurate summation of some awkward series
Published online by Cambridge University Press: 01 August 2016
Extract
In 1822 Joseph Fourier published an account of his work on the mathematical theory of heat. In his book Fourier considered the representation of a function f(x), which is defined on an interval such as 0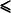 
x < 2π, by an infinite sum of trigonometric functions:
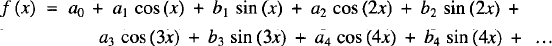
where the trailing dots indicate the sum goes on forever. The series is written more concisely with sigma notation as
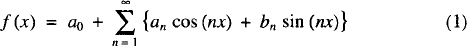
where x is restricted to an interval such as 0 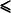x < 2π, and a0, an and bn are constant coefficients.
- Type
- Articles
- Information
- Copyright
- Copyright © Mathematical Association 1998
References
1.
Fourier, J., La theorie analytique de la chaleur, Paris (1822). (See The analytical theory of heat Trans. Freeman, A., Dover, New York, 1955.)Google Scholar
3.
Grattan-Guinness, I., The development of the foundations of mathematical analysis from Euler to Riemann, MIT Press, Cambridge, Mass. (1970).Google Scholar
4.
Bromwich, T-J.I.A., An Introduction to the theory of infinite series, 2nd revised ed. Macmillan (1926).Google Scholar
5.
Fitt, A.D. and Hoare, G.T.Q., The closed-form integration of arbitrary functions, Math. Gaz. 77 (July 1993) pp. 227–236.10.2307/3619719Google Scholar
6.
Herbert, E. and Tin, S.K., The Lobachevskiy’s function and related integrals, Inst, of Math, and its Applications Bulletin
27 (1991) p. 175–180.Google Scholar
7.
Abramowitz, M. and Stegun, I.A., Handbook of mathematical functions, Dover, New York (1965).Google Scholar