Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T15:05:33.147Z Has data issue: false hasContentIssue false
  • English
  • Français

Γ2 (½)is more than just π

Published online by Cambridge University Press:  23 January 2015

Samuel G. Moreno  and
Esther M. García-Caballero
Samuel G. Moreno
Affiliation:
Departamento de Matemáticas, Universidad de Jaén, 23071 Jaén, Spain
Esther M. García-Caballero
Affiliation:
Departamento de Matemáticas, Universidad de Jaén, 23071 Jaén, Spain
Get access Rights & Permissions [Opens in a new window]

Extract

For a fixed positive integer m, factorial m is defined by

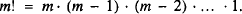
The problem of finding a formula extending the factorial m! to positive real values of m was posed by D. Bernoulli and C. Goldbach and solved by Euler. In his letter of 13 October 1729 to Goldbach [1], Euler defined a function (which we denote as Γ (x + 1)) by means of

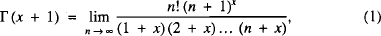
and showed that Γ (m + 1) = m! for positive integers m. After that, Euler found representations for the so-called gamma function (1) in terms of either an infinite product or an improper integral. We refer the reader to the classical (and short) treatise [2] for a brief introduction and main properties of the gamma function.

Type
Articles
Information
The Mathematical Gazette , Volume 97 , Issue 540 , November 2013 , pp. 430 - 434
Copyright
Copyright © The Mathematical Association 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. The Euler Archive, http://www.math.dartmouth.edu/~euler/ Google Scholar
2. Artin, E., The gamma function, Holt, Rinehart and Winston, New York (1964).Google Scholar
3. Melzak, Z. A., Infinite products for πe and π/e , Amer. Math. Monthly 68 (1961) pp. 39–41.Google Scholar
4. Adamchik, V. S., The multiple gamma function and its application to computation of series, Ramanujan J. 9 (2005) pp. 271–288.Google Scholar
5. Borwein, P., Dykshoorn, W., An interesting infinite product, J. Math. Anal. Appl. 179 (1993) pp. 203–207.Google Scholar
6. van der Pol, B., Note on the gamma function, Canadian J. Math. 6 (1954) pp. 18–22.Google Scholar
7. Nanjundiah, T. S., Van der Pol's expressions for the gamma function, Proc. Amer. Math. Soc. 9 (1958) pp. 305–307.Google Scholar
8. Weisstein, E., Euler-Mascheroni constant. From MathWorld, A Wolfram Web Resource. http://mathworld.wolfram.com/Euler-MascheroniConstant.html Google Scholar