2.1 The optimal trend inflation: Welfare effects and the ZLB

A crucial feature of an welfare-optimized monetary policy rule is the optimal level of inflation target (the chosen inflation trend) in the optimized rule. In our sticky-price and sticky-wage model, a positive trend inflation is costly to the economy through both a steady-state effect and dynamic effects. The former is the more important, so we examine this in some detail. For simplicity, consider the zero growth case $g=0$ for which wage and price inflation are equal. Then for price-setting the impact of trend inflation $\Pi$ on the deterministic steady state is given by

\begin{align*} \frac{P^{0}}{P} &= \left(\frac{1-\xi _p \Pi ^{(1-\gamma _p)(\zeta _p-1)}}{1-\xi _p}\right)^{\frac{1}{1-\zeta _p}} \\ \Delta _{p} &= \frac{1-\xi _p}{1-\xi _p\Pi ^{\zeta _p(1-\gamma _p)}} \left(\frac{P^0}{P}\right)^{-\zeta _p} \\ MC &= \left(1-\frac{1}{\zeta _p}\right) \frac{1-\xi _p \beta \Pi ^{\zeta _p(1-\gamma _p)}}{1-\xi _p \beta \Pi ^{(\zeta _p-1)(1-\gamma _p)}}\frac{P^{0}}{P} \end{align*}

where $\frac{P^{0}}{P}$ is the reoptimized Calvo-price for each retail variety, reset with probability $\xi _p$ , $\zeta _p$ is the price-elasticity of demand $\Delta _{p}$ is price dispersion across varieties, $MC$ is the real marginal cost equal to the inverse of the price mark-up, $\gamma _p \in [0,1]$ is the degree of price-indexing and $\beta$ is the household discount factor.Footnote ⁴

For wage-setting, we have analogous results:

\begin{align*} \frac{W_n^{O}}{W_n} &= \left(\frac{1-\xi _w \Pi ^{(1-\gamma _w)(\zeta _w-1)}}{1-\xi _w}\right)^{\frac{1}{1-\zeta _w}}\\ \Delta _{w} &= \frac{1-\xi _w}{1-\xi _w \Pi ^{(1-\gamma _w)\zeta _w}} \left(\frac{W_n^O}{W_n}\right)^{-\zeta _w}\\ \frac{W_{h}}{W} & =\frac{\left(1-\xi _w \beta \Pi ^{(1-\gamma _w)\zeta _w}\right)\left(1-\frac{1}{\zeta _w}\right)\frac{W_n^{O}}{W_n} }{1-\xi _w \beta \Pi ^{(1-\gamma _w)(\zeta _w-1)}}. \end{align*}

where $\frac{W_n^{O}}{W_n}$ is the reoptimized Calvo nominal wage for each labor variety, reset with probability $\xi _w$ , $\zeta _w$ is the wage elasticity of demand $\Delta _{w}$ is nominal wage dispersion across varieties, $\gamma _w \in [0,1]$ is the degree of nominal wage indexing and $\frac{W_{h}}{W}$ is the inverse of the real wage mark-up over the real wage homogeneous labor rate $W_{h}$ at which households supply hours.

Thus for $\zeta _p\gt 1$ , both the optimized price $\frac{P^{0}}{P}$ and price dispersion $\Delta _{p}$ increase with the trend inflation rate $\Pi$ . However, noting that the price mark-up is the inverse of the real marginal cost, that is, equal to $=1/MC$ , we can see that the price response to the reoptimized price decreases with $\Pi$ . Analogous results for $\zeta _w\gt 1$ hold for the optimized nominal wage, wage dispersion, and the wage mark-up which is the inverse of $\frac{W_{h}}{W_n}$ . Taking these results together, we then have two effects of trend inflation that increase distortions from sticky prices and wages and thus reduce welfare whereas the third effect results in the opposite. However, numerical results based on our estimated model confirms that the former easily outweighs the latter.Footnote ⁵

We now turn to the dynamic effect of trend inflation which was first studied by Ascari and Ropele (Reference Ascari and Ropele2007). They show it leads to richer inflation dynamics and a higher inflation volatility. They also show that the Taylor principle is no longer sufficient to guarantee a unique rational expectations equilibrium in New Keynesian models for even moderate levels of inflation. CGW argue that a greater steady-state inflation induces a higher level of its forward-looking dynamic behavior when sticky-price firms are able to reset their prices. The more forward-looking is a firm, the greater is then anticipation of other firms raising the optimal reset price. These dynamic considerations point to further welfare costs of high trend inflation. Fig. 1 previews the dynamic effects of trend inflation for the stochastic steady state of our estimated model, set out in the rest of the paper, with the CB choosing an optimized general interest rate rule that maximizes expected household intertemporal welfare (without, as yet, ZLB considerations).

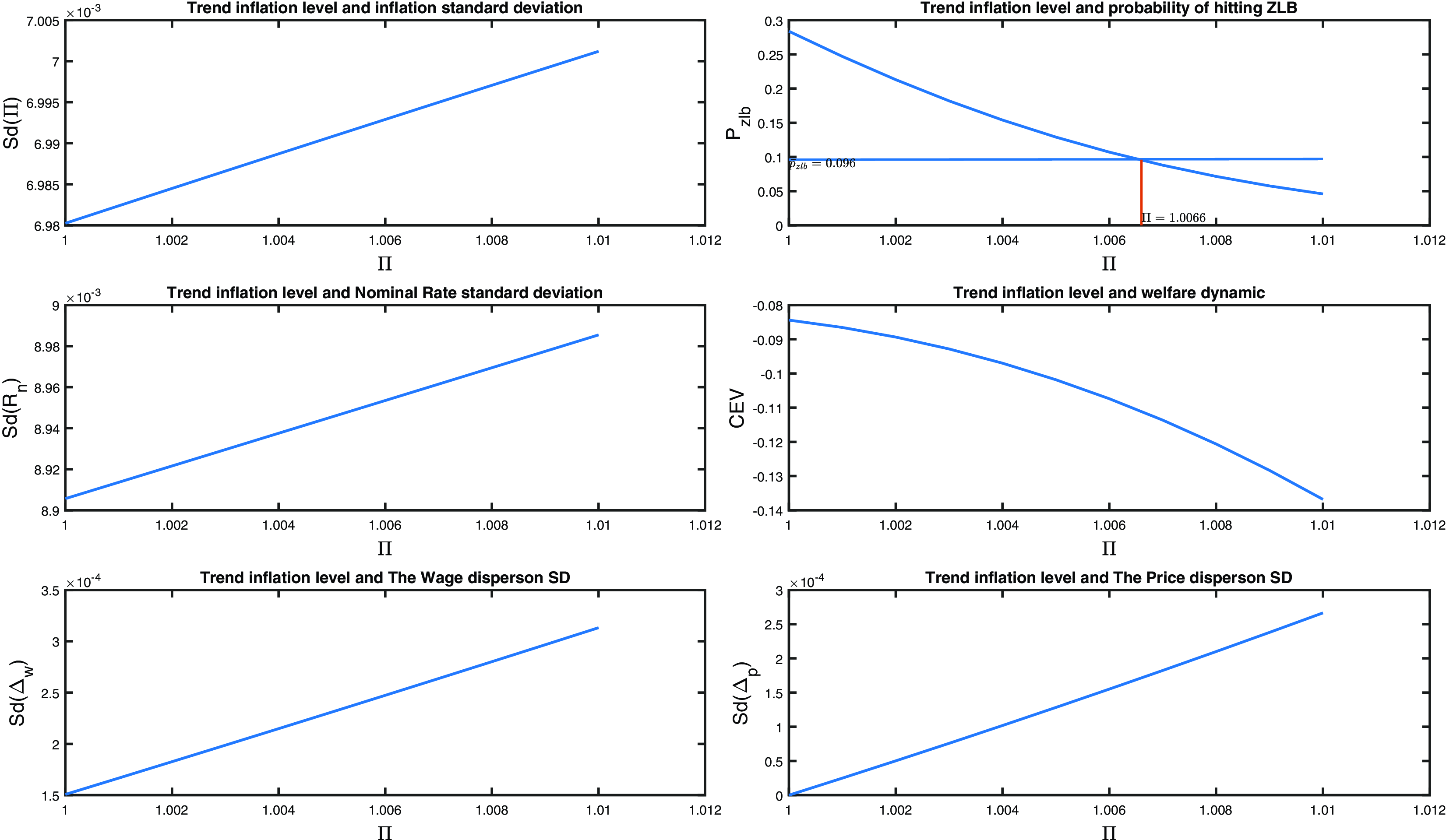
Figure 1. The effects of trend inflation, $\Pi$ , in the stochastic steady state. The consumption equivalent variations (CEV) is the welfare gain(loss) with different monetary regimes, expressing with different values of steady-state inflation, the representative household’s welfare compared to when the central bank pursues a monetary policy regime at the Ramsey. The figure is produced by stimulating the estimated Smets and Wouters (Reference Smets and Wouters2007) model (presented below) for different values of trend inflation.

We see the positive relationship between the level and volatility of inflation, a well-documented result in the empirical literature, associated with an increasing volatility of the nominal interest rate, $R_{n,t}$ . Thus, the distribution of $R_{n,t}$ as well as shifting to the right becomes wider. The net effect on the probability of hitting the ZLB can therefore be positive or negative, but given the estimation and optimized rule the first effect dominates and the probability falls.

A positive trend inflation then increases distortions caused by sticky prices and wages by increasing both the steady state and the volatility of both price and wage dispersion (see Fig. 1 for the latter) and is welfare-reducing. But on the other hand, a positive inflation trend reduces the frequency of the nominal interest rate hitting the ZLB constraint. Frequent ZLB incidents are an undesirable feature of a monetary rules because, as Christiano et al. (Reference Christiano, Eichenbaum and Rebelo2011) argue, a zero-bound scenario involves a deflationary spiral which contributes to and accompanies a large fall in output, which leads to a high volatility and large output cost. Specifically, when output falls, marginal cost falls and price declines. With staggered pricing, a drop in price causes agents to expect a deflation in the future. With the nominal interest rate stuck at zero, the real interest rate rises, which leads to an increase in desired saving and a decrease in output. As a result, the cumulative fall in output required to reduce desired saving to zero is extremely significant. These considerations lead us to design a monetary rule with a low probability of ZLB episodes.

Are there then welfare benefits from increasing trend inflation given the desirability of avoiding such adverse zero-bound episodes? Should then the optimal level of inflation target set by the central bank be close to the typical target inflation of 2% or is the inflation target too blunt an instrument to efficiently reduce the severe costs of zero-bound episodes. This is one of the research questions we now pursue in our general mandate framework.

2.2 The ZLB constraint through a penalty function

In this paper, we adopt a penalty function approach to the imposition of a ZLB constraint on the nominal net interest rate. It is distinguished from the imposition of a ZLB occasionally binding constraint. For the latter standard perturbation methods are unavailable as the policy function is nondifferentiable at the constraint, but the option of a global solution by value function iteration methods is possible (see, for example, Guerrieri and Iacoviello (Reference Guerrieri and Iacoviello2015)). However, this option suffers from the curse of dimensionality unless the state space is small. This problem becomes acute when the model solution is embedded in our mandate framework that involves the computation of optimized rules. Our solution then is to use an approximate perturbation-based method with a penalty function that imposes the constraint in a continuously binding form.

There are two common approaches to this method: first, to add the penalty term to the policy-maker’s welfare criterion (see Woodford, Reference Woodford2003), Giannoni and Woodford (Reference Giannoni and Woodford2003), Levine et al. (Reference Levine, McAdam and Pearlman2008b, Reference Levine, McAdam and Pearlman2012), Giannoni (Reference Giannoni2014)); second, to add the penalty term to the agents’ welfare criteria in the model (see Den Haan and Wind (Reference Den Haan and Wind2012), Abo-Zaid (Reference Abo-Zaid2015), Karmakar (Reference Karmakar2016)). The general idea is that instead of truncating the state space of the model at the constraint, we introduce a welfare penalty if the constraint is violated; this penalty acts as a constraint while maintaining differentiability of the policy functions. More precisely, we allow the nominal interest rate hit the zero bound with a small probability which can be interpreted as the tightness level of the ZLB constraint.Footnote ⁶ Our paper follows this literature by adding a penalty term on the central bank’s objective function. We also compare different mandate formations delegated to the central bank, namely: a so-called ZLB mandate which retains the household utility as a welfare measure, a number of simple quadratic loss function mandates, and an asymmetric functional form mandate.

2.3 The delegation game

We now turn to simple quadratic loss function mandates designed to increase transparency in the conduct of monetary policy. In the simple mandates we choose the particular loss function is matched with a simple rule with the same targets. Thus, the transparency of the loss function is reinforced with that of the interest rate rule. Our mandates are expressed in terms of the growth of a real variable $X_t$ , $\frac{X_t}{X_{t-1}}$ and gross inflation $\Pi _t$ relative to their steady states. In the simple mandates, we study the real variable can be output, the real market-clearing wage paid by the firm and hours employed. The mandate delegated to the central bank then consists of a welfare criterion:

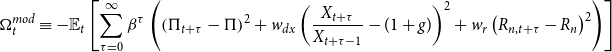(1) \begin{eqnarray} \Omega _t^{mod} \equiv - \mathbb{E}_t\left [ \sum _{\tau =0}^\infty \beta ^{\tau } \left(\left(\Pi _{t+\tau } - \Pi \right)^2 + w_{dx} \left(\frac{X_{t+\tau }}{X_{t+\tau -1}} - (1+g) \right)^2 + w_r \left(R_{n,t+\tau } - R_n \right)^2 \right) \right ] \end{eqnarray}

with a corresponding simple rule for the nominal gross interest rate $R_{n,t}$ , the monetary instrument given by

(2) \begin{equation} \log \left( \frac{R_{n,t}}{R_n}\right)=\rho _r \log \left( \frac{R_{n,t-1}}{R_n}\right) +\alpha _\pi \log \left(\frac{\Pi _{t}}{\Pi }\right) + \alpha _{dx} \log \left(\frac{X_t}{X_{t-1}}\right) \end{equation}

A two-stage quadratic loss function delegation game then defines an equilibrium in choice variables by the leader (the policymaker) $w_{dx}^*$ , $w_r^*$ , and $\Pi ^*$ and a choice $\rho ^* \equiv [ \rho _r^*, \alpha _\pi ^*, \alpha _{dx}^*]$ by an independent central bank (the follower) that maximizes the actual household welfare subject to the ZLB constraint that maximizes the actual household intertemporal welfare given by

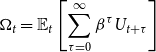(3) \begin{eqnarray} \Omega _t=\mathbb{E}_t\left [ \sum _{\tau =0}^\infty \beta ^{\tau } U_{t+\tau }\right ] \end{eqnarray}

where $U_t$ is the single-period utility of the representative household. The central bank is instrument independent in the sense that it is free to choose $\rho ^*$ given the mandate that specifies its objective (1) and form of rule (2).

In an intermediate regime we first examine a ZLB delegation game with a modified welfare measure delegated to the central bank based on (3) with a penalty term designed to limit the variance of the nominal interest rate:

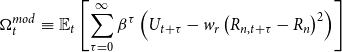(4) \begin{eqnarray} \Omega _t^{mod} &\equiv & \mathbb{E}_t\left [ \sum _{\tau =0}^\infty \beta ^{\tau } \left(U_{t+\tau } - w_r \left(R_{n,t+\tau } - R_n \right)^2 \right)\right ] \end{eqnarray}

and a simple Taylor-type rule of the same form as that estimated in Section 4.

(5) \begin{equation} \log \left( \frac{R_{n,t}}{R_n}\right)=\rho _r \log \left( \frac{R_{n,t-1}}{R_n}\right) +\alpha _\pi \log \left(\frac{\Pi _{t}}{\Pi }\right) + \alpha _y \log \left(\frac{Y_t}{Y}\right) + \alpha _{dy} \log \left(\frac{Y_t}{Y_{t-1}}\right) \end{equation}

Our welfare criteria $\Omega _t^{mod}$ and $\Omega _t$ are conditional, evaluated at the deterministic zero net inflation steady state and responding to all future shocks. We distinguish two welfare criteria in this delegation game: first, the modified welfare, $\Omega _t^{mod}$ , is the welfare criterion of the central bank. Second, the actual welfare, $\Omega _t$ , is the welfare criterion of the representative household. Full details of these two delegation games are given in Sections 5 and 6.

Two research question regarding the mandates are then first, what is the cost of simplicity in adopting quadratic mandate compared with the benchmark as the ZLB constraint becomes tighter and second, what are the relative weights attached to real economic activities compared with the (unit) weight attached to price inflation.

3.1 Households

At time $t=0$ , household $i$ maximizes its expected lifetime utility

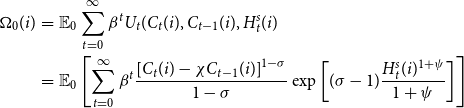(6) \begin{eqnarray} \Omega _0(i)&=&\mathbb{E}_0 \sum _{t=0}^\infty \beta ^t U_t(C_t(i), C_{t-1}(i), H_t^s(i)\nonumber \\&=&\mathbb{E}_0 \left [\sum _{t=0}^\infty \beta ^t \frac{\left [C_t(i)-\chi C_{t-1}(i)\right ]^{1-\sigma }}{1-\sigma }\exp \left [(\sigma -1)\frac{ H_t^s(i)^{1+\psi }}{1+\psi }\right ]\right ] \end{eqnarray}

where $\mathbb{E}_t[\cdot ]$ denotes rational expectations based on information available at time $t$ , $C_t(i)$ is real consumption, $H_t^s(i)$ is hours supplied, $\beta$ is the discount factor, $\chi$ controls for internal habit formation, $\sigma$ is the inverse of the elasticity of intertemporal substitution (for constant labor), and $\psi$ is the inverse of the Frisch labor supply elasticity. Preferences chosen by SW in (6) are compatible with balanced growth (see King et al. (Reference King, Plosser and Rebelo1988)).

The household’s budget constraint in period $t$ is given by

(7) \begin{equation} C_t(i) + I_t(i) + \frac{B_{t}(i)}{RPS_t R_{n,t} P_t} + T_t = \frac{B_{t-1}(i)}{P_t}+ \left(r_t^K u_t(i) - a(u_{t}(i))\right)K_{t-1}(i) + W_{h,t} H_t^s(i)+\Gamma _t \end{equation}

where $I_t$ is investment into physical capital, $B_t$ is government bonds held at the end of period $t$ , $R_{n,t-1}$ is the nominal interest rate paid on government bonds held at the beginning of period $t$ , $RPS_t$ is an exogenous premium in the return on bonds that follows an AR1 process. $T_t$ is lump-sum taxes, $r_t^K$ is the real rental rate, $u_t$ is the utilization rate of capital, $\mbox{IS}_t$ is an investment specific technological shock (the inverse of the relative price of new capital in consumption terms), $a(u_t(i))$ is the physical cost of use of capital in consumption terms, $W_{h,t}$ is the real wage rate at which households supply labor that is homogeneous at this point to trade unions and $\Gamma _t$ is the profit of intermediate firms distributed to households.

End of period capital stock, $K_t(i)$ , accumulates according to

(8) \begin{align} K_{t}(i)&= (1-\delta ) K_{t-1}(i)+(1-S(X_t(i)))I_t(i) \mbox{IS}_t \end{align}

where $\mbox{IS}_t$ is an investment specific technological shock that follows an AR1 process, $X_t(i) = I_t(i)/I_{t-1}(i)$ is the growth rate of investment, and $S(\cdot )$ is an adjustment cost function such that $S(X)=0$ , $S'(X)=0$ , and $S''(\cdot )=0$ where $X$ is the steady-state value of investment growth. For $S(X_t)$ in a symmetric equilibrium, we choose the functional form: $S(X_t)=\phi _X (X_t-\bar{X}_t)^2$ where $\bar{X}_t$ is the balanced-growth steady-state trend. For $a(u_t)$ we choose the functional form: $a(u_t)=\gamma _1(u_t-1)+\frac{\gamma _2}{2}(u_t-1)^2$ with $u_t=u=1$ in the steady state.

Then the household first-order conditions consist of an Euler Consumption equation, an arbitrage condition, a first-order condition equating the marginal rate of substitution between leisure and consumption with the real wage and first-order conditions for investment, the price of capital $Q_t$ (Tobin’s Q) and capacity utilization:

(9) \begin{align} \mathbb{E}_t[\Lambda _{t,t+1}(i) R_{t+1}]&=1 \end{align}

(10) \begin{align} \mathbb{E}_t[\Lambda _{t,t+1}(i) R_{t+1}^K]& =1 \end{align}

(11) \begin{align} -\frac{U_{H,t}(i)}{U_{C,t}(i)} & =W_{h,t} \end{align}

(12) \begin{align} Q_t & = \mathbb{E}_t \left \{\Lambda _{t,t+1}(i) \left [r_{t+1}^K u_{t+1}(i) - a(u_{t+1})(i) + Q_{t+1} (1-\delta )\right ]\right \} \end{align}

(13) \begin{align} 1 &= Q_t\left [1-S(X_t(i))-S'(X_t)(i)X_t(i)\right ]IS_t\nonumber \\ &\quad + \mathbb{E}_{t} \left [\Lambda _{t,t+1} Q_{t+1} S'(X_{t+1}(i))X_{t+1}(i)^2 IS_{t+1} \right ] \end{align}

(14) \begin{align} r_t^K & =a'(u_t(i)) \end{align}

where $\Lambda _{t,t+1}(i)\equiv \beta \frac{U_{C,t+1}(i)}{U_{C,t}(i)}$ is the stochastic discount factor, $U_{C,t}(i) \equiv \frac{\partial U_t(i) }{\partial C_t(i)}$ , $U_{H,t} (i) \equiv \frac{\partial U_t(i) }{\partial H_t(i)}$ are marginal utilities over two successive periods in the summation given by

(15) \begin{equation} U_{C,t} (i) = (1-\sigma ) \left( \frac{U_t(i)}{C_t(i)-\chi C_{t-1}(i)} -\frac{\beta \chi U_{t+1}(i)}{C_{t+1}(i)-\chi C_{t}(i)} \right) \end{equation}

$R_t = \frac{R_{n,t-1}}{\Pi _t}$ and $R_{t}^K=\frac{[r_t^K u_t-a(u_t)+(1-\delta )Q_{t}]}{Q_{t-1}}$ are the real gross returns on government bonds and physical capital, respectively, and $Q_t$ is the price of capital (Tobin’s Q). In a symmetric equilibrium of identical households $C_t(i)=C_t$ , $H_t^s (i) =H_t^s$ , etc.

3.2 The labor market

Households supply their homogeneous labor to trade unions that differentiate the labor services. A labor packer buys the differentiated labor from the trade unions and aggregate them into a composite labor using the Dixit–Stigliz aggregatorFootnote ⁹ given aggregate demand $H_t^d$ .

(16) \begin{equation} H_{t}^d=\left( \int _{0}^{1}H_{t}(j)^{(\zeta _w -1)/\zeta _w }dj\right)^{\zeta _w/(\zeta _w -1)} dj \end{equation}

where $\zeta _w$ is the elasticity of substitution among different types of labor, and we index trade unions by $j$ . The labor packer minimizes the cost $\int _0^1 W_{n,t}(j) H_t(j) dj$ of producing the composite labor service, where $W_{n,t}(j)$ denotes the nominal wage set by union $j$ . This leads to the standard demand function

(17) \begin{align} H_{t}(j)&=\left(\frac{W_{n,t}(j)}{W_{n,t}}\right) ^{-\zeta _w }H_{t}^d \end{align}

where $W_{n,t}$ is the aggregate nominal wage given by the Dixit–Stigliz aggregator

\begin{equation*} W_{n,t}=\left [ \int _0^1 W_{n,t}(j)^{1-\zeta _w} dj \right ]^{ \frac {1}{1-\zeta _w}} \end{equation*}

Sticky wages are introduced through Calvo contracts supplemented with indexation. At each period there is a probability $1-\xi _{w}$ that trade union $j$ can choose $W_{n,t}^O(j)$ to maximize

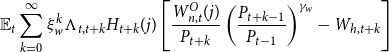\begin{equation*} \mathbb {E}_t \sum _{k=0}^\infty \xi _w^k \Lambda _{t,t+k} H_{t+k}(j) \left [\frac {W_{n,t}^O(j)}{P_{t+k}}\left(\frac {P_{t+k-1}}{P_{t-1}}\right)^{\gamma _w} - W_{h,t+k} \right ] \end{equation*}

subject to the demand function (17), where $\gamma _w \in [0,1]$ is a wage indexation parameter.

The solution to the above problem is the first-order condition

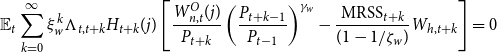\begin{equation*} \mathbb {E}_t\sum _{k=0}^{\infty } \xi _w^k \Lambda _{t,t+k} H_{t+k}(j)\left [\frac {W_{n,t}^{O}(j)}{P_{t+k}} \left(\frac {P_{t+k-1}}{P_{t-1}}\right)^{\gamma _w}-\frac {\mbox {MRSS}_{t+k}}{(1-1/\zeta _w)} W_{h,t+k}\right ] =0 \end{equation*}

where we have introduced a mark-up shock $\mbox{MRSS}_t$ to the marginal rate of substitution that follows an AR1 process. This leads to

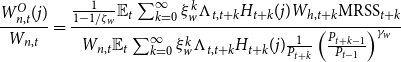\begin{align*} \frac{W_{n,t}^{O}(j)}{W_{n,t}} &= \frac{\frac{1}{1-1/\zeta _w}\mathbb{E}_t\sum _{k=0}^{\infty } \xi _w^k \Lambda _{t,t+k}H_{t+k}(j)W_{h,t+k}\mbox{MRSS}_{t+k}}{W_{n,t} \mathbb{E}_t\sum _{k=0}^{\infty } \xi _w^k \Lambda _{t,t+k}H_{t+k}(j)\frac{1}{P_{t+k}}\left(\frac{P_{t+k-1}}{P_{t-1}}\right)^{\gamma _w}} \end{align*}

where $\frac{W_{n,t}^{O}(j)}{W_{n,t}}=\frac{W_{n,t}^{O}}{W_{n,t}}$ in a symmetric equilibrium.

By the law of large numbers the evolution of the aggregate wage is given by

\begin{equation*} W_{n,t}^{1-\zeta _w} = \xi _w \left(W_{n,t-1}\Pi _{t-1}^{\gamma _w}\right)^{1-\zeta _w}+(1-\xi _w)(W_{n,t}^{O})^{1-\zeta _w } \end{equation*}

which can be written as

(18) \begin{equation} 1 = \xi _w \left(\frac{\Pi _{t-1}^{\gamma _w}}{\Pi _t^w}\right)^{1-\zeta _w}+(1-\xi _w)\left(\frac{W_{n,t}^O}{W_{n,t}}\right)^{1-\zeta _w} \end{equation}

Wage dispersion is defined as $\Delta _{w,t}=\int (W_{n,t}(j)/W_{n,t})^{-\zeta _w} dj$ . Assuming that the number of trade unions is large, we obtain the following dynamic relationship:

\begin{align*} \Delta _{w,t} &= \xi _w\int _{not\ optimize} \left(\frac{W_{n,t-1}^O(j)\Pi _{t-1}^{\gamma _w}}{W_{n,t}}\right)^{-\zeta _w} dj + (1-\xi _w)\int _{optimize} \left(\frac{W_{n,t}^O(j)}{W_{n,t}}\right)^{-\zeta _w} dj \\ &= \xi _w \frac{(\Pi _t^w)^{\zeta _w}}{\Pi _{t-1}^{\zeta _w\gamma _w}} \Delta _{w,t-1}+(1-\xi _w)\left(\frac{W_{n,t}^O(j)}{W_{n,t}}\right)^{-\zeta _w} \end{align*}

3.3 Firms in the wholesale sector

Wholesale firms employ a Cobb–Douglas production function to produce a homogeneous output

\begin{equation*} Y_t^W = F(A_t, H_t^d, u_t K_{t-1}) = (A_t H_t^d)^\alpha (u_tK_{t-1})^{1-\alpha } - F_t \end{equation*}

where $F_t$ are exogenous fixed costs growing in a balanced-growth steady in line with the other real variables. Profit-maximizing demand for factors results in the first order conditions

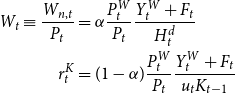\begin{align*} W_t \equiv \frac{W_{n,t}}{P_t} &= \alpha \frac{P_t^W}{P_t}\frac{Y_t^W + F_t}{H_t^d} \\ r_t^K &= (1-\alpha ) \frac{P_t^W}{P_t}\frac{Y_t^W + F_t}{u_tK_{t-1}} \end{align*}

3.4 Firms in the retail sector

The retail sector uses a homogeneous wholesale good to produce a basket of differentiated goods for aggregate consumption

(19) \begin{equation} C_{t}=\left( \int _{0}^{1}C_{t}(m)^{(\zeta _p -1)/\zeta _p }dm\right) ^{\zeta _p/(\zeta _p -1)} \end{equation}

where $\zeta _p$ is the elasticity of substitution. For each $m$ , the consumer chooses $C_t(m)$ at a price $P_t(m)$ to maximize (19) given total expenditure $\int _0^1 P_t(m) C_t(m) dm$ . This results in a set of consumption demand equations for each differentiated good $m$ with price $P_{t}(m)$ of the form

\begin{equation*} C_{t}(m)=\left( \frac {P_{t}(m)}{P_{t}}\right) ^{-\zeta _p }C_{t}\Rightarrow Y_{t}(m)=\left( \frac {P_{t}(m)}{P_{t}}\right) ^{-\zeta _p }Y_{t} \end{equation*}

where $P_{t}={\left [ \int _0^1 P_{t}(m)^{1-\zeta _p} dm \right ]}^{ \frac{1}{1-\zeta _p}}$ . $P_{t}$ is the aggregate price index. $C_t$ and $P_t$ are Dixit–Stigliz aggregates—see Dixit and Stiglitz (Reference Dixit and Stiglitz1977).

Following Calvo (Reference Calvo1983), we now assume that there is a probability of $1-\xi _p$ at each period that the price of each retail good $m$ is set optimally to $P_{t}^{0}(m)$ . If the price is not reoptimized, then prices are indexed to last period’s aggregate inflation, with indexation parameter $\gamma _{p}$ . With indexation parameter $\gamma _p \geq 0$ , this implies that successive prices with no reoptimization are given by $P_{t}^{0}(f)$ , $P_{t}^{0}(f)\left(\frac{P_{t}}{P_{t-1}}\right)^{\gamma _p}$ , $P_{t}^{0}(f)\left(\frac{P_{t+1}}{P_{t-1}}\right)^{\gamma _p}$ , $\ldots$ . For each retail producer $m$ , given its real marginal cost (the inverse of the price mark-up)

\begin{equation*} MC_t=\frac {P_t^W}{P_t}, \end{equation*}

the objective is at time $t$ to choose $\{P_{t}^O(m)\}$ to maximize discounted profits

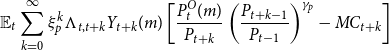\begin{equation*} \mathbb {E}_t\sum _{k=0}^{\infty } \xi _p^k \Lambda _{t,t+k} Y_{t+k}(m) \left [\frac {P_{t}^{O}(m)}{P_{t+k}}\left(\frac {P_{t+k-1}}{P_{t-1}}\right)^{\gamma _p}- MC_{t+k}\right ] \end{equation*}

subject to

\begin{equation*} Y_{t+k}(m)=\left [\frac {P_{t}^O(m)}{P_{t+k}}\left(\frac {P_{t+k-1}}{P_{t-1}}\right)^{\gamma _p}\right ] ^{-\zeta _p }Y_{t} \end{equation*}

The solution to this is

\begin{equation*} \mathbb {E}_t\sum _{k=0}^{\infty } \xi _p^k \Lambda _{t,t+k} Y_{t+k}(m)\left [\frac {P_{t}^{O}(m)}{P_{t+k}} \left(\frac {P_{t+k-1}}{P_{t-1}}\right)^{\gamma _p}-\frac {1}{(1-1/\zeta _p)} MC_{t+k}\right ] =0 \end{equation*}

which leads to

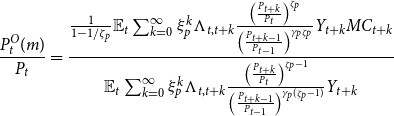\begin{equation*} \frac {P_{t}^{O}(m)}{P_t} = \frac {\frac {1}{1-1/\zeta _p}\mathbb {E}_t\sum _{k=0}^{\infty } \xi _p^k \Lambda _{t,t+k}\frac {\left(\frac {P_{t+k}}{P_{t}}\right)^{\zeta _p}}{\left(\frac {P_{t+k-1}}{P_{t-1}}\right)^{\gamma _p\zeta _p}}Y_{t+k}MC_{t+k}}{\mathbb {E}_t\sum _{k=0}^{\infty } \xi _p^k \Lambda _{t,t+k}\frac {\left(\frac {P_{t+k}}{P_{t}}\right)^{\zeta _p-1}}{\left(\frac {P_{t+k-1}}{P_{t-1}}\right)^{\gamma _p(\zeta _p-1)}}Y_{t+k}} \end{equation*}

where $\frac{P_{t}^{O}(m)}{P_t}=\frac{P_{t}^{O}}{P_t}$ in a symmetric equilibrium.

By the law of large numbers the evolution of the price index is given by

\begin{equation*} P_{t}^{1-\zeta _p }=\xi _p \left(P_{t-1}\Pi _{t-1}^{\gamma _p}\right)^{1-\zeta _p}+(1-\xi _p)(P_{t}^{O}(m))^{1-\zeta _p } \end{equation*}

which can be written as

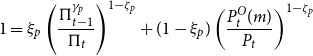\begin{equation*} 1 = \xi _p \left(\frac {\Pi _{t-1}^{\gamma _p}}{\Pi _t}\right)^{1-\zeta _p}+(1-\xi _p)\left(\frac {P_{t}^O(m)}{P_{t}}\right)^{1-\zeta _p} \end{equation*}

Price dispersion is defined as $\Delta _{p,t}=\int (P_t(m)/P_t)^{-\zeta _p} dm$ . Assuming that the number of firms is large, we obtain the following dynamic relationship:

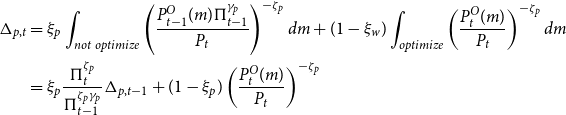\begin{align*} \Delta _{p,t} &= \xi _p \int _{not\ optimize} \left(\frac{P_{t-1}^O(m)\Pi _{t-1}^{\gamma _p}}{P_t}\right)^{-\zeta _p} dm + (1-\xi _w)\int _{optimize} \left(\frac{P_{t}^O(m)}{P_t}\right)^{-\zeta _p} dm \\ &= \xi _p \frac{\Pi _t^{\zeta _p}}{\Pi _{t-1}^{\zeta _p\gamma _p}} \Delta _{p,t-1}+(1-\xi _p)\left(\frac{P_t^O(m)}{P_t}\right)^{-\zeta _p} \end{align*}

3.5 Closing the model

The model is closed with a resource constraint

\begin{equation*} Y_{t} = C_{t} + G_t + I_t + a(u_{t}) K_{t-1} \end{equation*}

A monetary policy rule for the nominal interest rate is given by the following Taylor-type rule

(20) \begin{align} \log \left( \frac{R_{n,t}}{R_n}\right) &= \rho _r \log \left( \frac{R_{n,t-1}}{R_n}\right) \nonumber \\ &\quad + (1-\rho _r)\left(\theta _{\pi } \log \left(\frac{\Pi _{t}}{\Pi }\right) + \theta _y \log \left(\frac{Y_t}{Y}\right) + \theta _{dy} \log \left(\frac{Y_t}{Y_{t-1}}\right)\right) \nonumber \\ &\quad + \log (MPS_t), \end{align}

where $MPS_t$ is a monetary policy shock and $\rho _r \in [0,1]$ . Our rule is of the implementable form as proposed by Schmitt-Grohe and Uribe (Reference Schmitt-Grohe and Uribe2007) in that the nominal interest rate responds to deviations of output about its steady state rather than deviations about the flexi-price level of output (i.e., the output gap). The latter would encompass the original rules proposed by Taylor (Reference Taylor1993) and (Reference Taylor and Taylor1999) for which there is no interest-rate smoothing ( $\rho _r=0$ ) and $\theta _{dy}=0$ . In the more recent of these papers, parameter values $\theta _{\pi }=1.5$ and $\theta _{y}=1.0$ are proposed.Footnote ¹⁰

Nominal and real interest rates are related by the Fischer equation

\begin{equation*} R_{t}=\left [ \frac {R_{n,t-1}}{\Pi _{t}} \right ] \end{equation*}

Market clearing for the labor market implies

\begin{equation*} H_t = \int _0^1 H_t(j) dj= \int _0^1\left(\frac {W_{n,t}(j)}{W_{n,t}}\right)^{-\zeta _w} dj H_t^d= \Delta _{w,t} H_t^d \end{equation*}

Market clearing for the final good market implies

\begin{equation*} Y_t^W = \Delta _{p,t} Y_t \end{equation*}

For completeness we include a government budget constraint

\begin{align*} P_t G_t + B_{t-1} = T_t + \frac{B_t}{R_{n,t}} \end{align*}

where $G_t$ is government spending that follows an AR1 process. However, in this Ricardian set-up without distortionary taxes the constraint plays no role in the equilibrium.

Finally, the seven exogenous processes are AR1 and evolve according to

\begin{equation*} \log \Xi _t-\log \Xi =\rho _\Xi (\log \Xi _{t-1}-\log \Xi ) +\epsilon _{\Xi,t} \end{equation*}

where $\Xi =A,\,G,\,MS,\,MRSS,\,IS,\,RPS,\,MPS$ .

3.6 Departures from Smets and Wouters (Reference Smets and Wouters2007)

The following are features that differ from Smets and Wouters (Reference Smets and Wouters2007):

Kimball vs Dixit-Stiglitz aggregators: SW use Kimball aggregators with a super elasticity of $10$ . But empirical evidence by Klenow and Willis (Reference Klenow and Willis2016) suggests a much lower value which removes any discernable difference between the two (see Deak et al. (Reference Deak, Levine, Mirfatah and Swarbrick2023)). We therefore retain the Dixit–Stiglitz aggregators.

Indexing and Trend Inflation: SW assume complete indexing in the steady state which removes all the trend inflation effects in our paper. We remove this assumption (see Ascari and Sbordone (Reference Ascari and Sbordone2014) for a discussion of indexation assumptions and the role of trend-inflation).

Shock Processes: We assume AR 1 shock processes throughout where SW assumes ARMA for inefficient mark-up shocks. Results are not sensitive to this assumption.

Sample Period: Estimation is over 1958:1–2017:4 and therefore unlike SW covers the ZLB period. We use the Mu-Xia shadow interest rate to replace the FEDFUNDs rate from 2009:1 onward intended to summarize the effects of unconventional monetary policy on private sector interest rates.

4.1 Data and measurement equations

Our observables used in the estimation are: GDP per capita growth (dyobs), consumption expenditure per capita growth (dcobs), investment per capita growth (dinvobs), real wage growth (dwobs), percentage deviation of hours worked per capita from mean (labobs), monetary policy rate (robs), and inflation rate (pinfobs). The corresponding measurement equations expressed in terms of stationarized variablesFootnote ¹² are

\begin{align*} \mbox{dyobs} &= \log \left((1+g)\frac{Y_{t}}{Y_{t-1}}\right)\end{align*}

\begin{align*} \mbox{dcobs} &= \log \left((1+g)\frac{C_{t}}{C_{t-1}}\right) \\ \mbox{dinvobs} &= \log \left((1+g)\frac{I_{t}}{I_{t-1}}\right) \\ \mbox{dwobs} &= \log \left((1+g)\frac{W_{t}}{W_{t-1}}\right) \\ \mbox{labobs} &= \frac{H_t^d - H^d}{H^d} \\ \mbox{robs} &= R_{n,t} - 1 \\ \mbox{pinfobs}&= \log \left(\Pi _t\right) \end{align*}

The steady-state values of the observables are dyobs=dinvobs=dcobs=dwobs= $\log (1+g)$ , labobs = 0, robs= $R_n-1$ , and pinfobs= $\log (\Pi )$ .

The original data are taken from the FRED Database available through the Federal Reserve Bank of St. Louis for the US economy. The data consists of 7 quarterly time series, namely log output growth ( $dyobs$ ), log consumption growth ( $dcobs$ ), log investment growth ( $dinvobs$ ), log wage growth ( $dwobs$ ), labor hours supply ( $labobs$ ), the net inflation ( $pinfobs$ ), and finally the policy rate measurement ( $robs$ ), because our focus on the ZLB we provide an estimation with the Wu-Xia Shadow interest rate replacing the FEDFUNDS rate, $robs$ —see Wu & Xia, Reference Wu and Xia2016). The sample period is 1958:1–2017:4. There is a presample period of 4 quarters so the observations actually used for the estimation go from 1959:1-2017:4, 240 observations (Table 1).

Table 1. St. Louis FRED original data

We then calculate the log growth rates of output ( $dyobs$ ), consumption ( $dcobs$ ), investment ( $dinvobs$ ), and wage ( $dwobs$ ) by taking the first difference of $yobs$ , $cobs$ , $invobs$ , and $wobs$ , respectively. The shadow Federal Funds Rate data are taken from the Federal reserve Bank of Atlanta. Wu & Xia (Reference Wu and Xia2016) propose a simple analytical representation for bond prices in the multifactor shadow rate term structure model. Unlike the observed short-term interest rate, the shadow rate is not bounded below by 0 percent. Whenever the Wu-Xia shadow rate is above 0.25% per annum (approximately 0.25/4% per quarter), it is exactly equal to the Federal Funds Effective Rate (FEDFUNDS). The model proposed in Wu & Xia Reference Wu and Xia(2016) summarizes the macroeconomic effects of unconventional monetary policy, that is, at the ZLB of the nominal interest rate. Common literature focused on measuring the effects on the yield curve, but this posed a challenge to measure the relations between the yields on assets of different maturities in the new environment, that is, during the ZLB period where the unconventional monetary policy is implemented. Therefore, the multifactor shadow rate term structure model offers a better empirical description of the behavior of interest rates during the ZLB period.

4.2 Identification and information assumptions

It is necessary to confront the question of parameter identifiability in DSGE models before taking them to the data, as model or parameter identification is a prerequisite for the informativeness of different estimators, and their effectiveness when one uses the models to address policy questions. Hence, we follows Iskrev (Reference Iskrev2010), Iskrev and Ratto (Reference Iskrev and Ratto2010) to perform formal identification checks on the reduced form parameters and structure or deep parameters. Overall, our identification analysis using dynare Dynare (2023) shows that the Jacobian and Hessian matrices of the mapping from the reduced form of the estimated parameters into the first and second order moments of the observable variables are full rank. Thus, our estimated model is locally identifiable given the priors and observable data sample. Details of this analysis are shown in the Online Appendix.

There is one more issue to address regarding the assumed information set of the agents in the model. Most DSGE models are still solved and/or estimated on the assumption that agents are simply provided with perfect information (henceforth PI) regarding the states including the exogenous processes, effectively as an endowment. If we drop this implausible assumption we must consider a signal extraction problem under imperfect information (II) for the agents in the model analogous to that we have considered for the econometrician. Fortunately we can retain the PI solution if we restrict ourselves to a class of models which are ‘A-invertible’ meaning that agents can infer the structural shocks from the information set assumed to be that of the econometrician. Levine et al. (Reference Levine, Pearlman, Wright and Yang2019) provide an A-invertibility condition that generalizes the “Poor Man’s Invertibility Condition” of Fernandez-Villaverde et al. (Reference Fernandez-Villaverde, Rubio-Ramirez, Sargent and Watson2007) and show that in the Smets and Wouters (Reference Smets and Wouters2007) of this paper with seven shock processes and seven observables is indeed A-invertible.Footnote ¹³ It follows that II and PI solutions coincide and the standard information assumption is valid in our model.

4.3 Estimation results

Table 2 indicates the priors, the estimated posterior mode of the parameters obtained directly from the maximization of the posterior distribution, and the mean of the posterior distribution of the parameters obtained through the Metropolis–Hastings sampling algorithm of our estimation.Footnote ¹⁴ The priors on the stochastic processes are identical to Smets and Wouters (Reference Smets and Wouters2007). The standard errors of the innovations are assumed to follow an inverse-gamma distribution with a mean of 0.001 (Smets and Wouters (Reference Smets and Wouters2007) use unscaled data with mean priors at 0.1) and 0.02 degrees of freedom (2 in Smets and Wouters (Reference Smets and Wouters2007)), which corresponds to a rather loose prior. The persistence of the AR(1) processes is beta distributed with mean 0.5 and standard error 0.2. Unlike Smets and Wouters (Reference Smets and Wouters2007) who estimated the trend growth with normal distribution of mean 0.4% and standard deviation of 0.1, we fix this trend growth at the empirical value of 0.355%. We also empirically calibrate the steady state of inflation, discount factor, and steady state of shadow interest rate by using the sample data.

Table 2. Estimated results (posterior mean with a number of draws equal to 100,000)

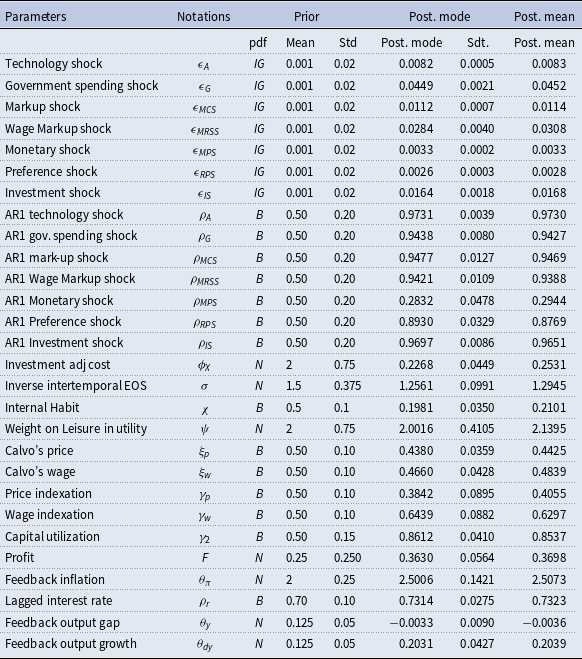
The parameters describing the monetary policy rule are based on a standard Taylor rule: the long run reaction on inflation and the output gap are described by a normal distribution with mean 2.0 and 0.125 (0.5 divided by 4) and standard errors 0.25 and 0.05, respectively. The persistence of the policy rule is determined by the coefficient on the lagged interest rate rate, which is assumed to be Beta distribution with mean of 0.75 with a standard error of 0.1. The prior on the short run reaction coefficient to the change in the output growth is normal distribution with mean 0.125 standard error 0.05.

The parameters of the utility function are assumed to be distributed as follows: the intertemporal elasticity of substitution is set at 1.5 with a standard error of 0.375; the habit parameter is assumed to fluctuate around 0.5 with a standard error of 0.1 and the elasticity of labor supply is assumed to be around 2 with a standard error of 0.75. These are all quite standard calibrations. The prior on the adjustment cost parameter for investment is set around 2 with a standard error of 0.75 and the capacity utilization elasticity is set at 0.5 with a standard error of 0.15. The share of fixed costs in the production function is assumed to have a prior mean of 0.25. Finally, there are the parameters describing the price and wage setting. The Calvo probabilities are assumed to be around 0.5 for both prices and wages, suggesting an average length of price and wage contracts of half a year. The prior mean of the degree of indexation to past inflation is also set at 0.5 in both goods and labor markets. These priors are standard as in Smets and Wouters (Reference Smets and Wouters2007).

Overall, all estimated parameters are significantly different from zero. Most of the persistent shocks are estimated to have an autoregressive parameter that lies above 0.9, with the exception of the estimated persistent parameter on monetary policy shock standing at 0.31. In addition, we find that the estimated price indexation parameter is smaller than the mean assumed in their prior distribution, $\gamma _p = 0.40$ , but wage indexation is higher at $\gamma _w = 0.63$ . Moreover, the estimated Calvo’s price and wage parameters are relatively small at $\xi _p = 0.44$ and $\xi _w = 0.48$ , but taken together these estimates represent a significant degree of price and wage stickiness and departure from full indexation. Thus, a positive trend inflation leads to a significant welfare cost owing to both steady state and dynamic costs discussed in Section 2.1. Besides, other estimated parameters’ values are consistent with the results from Smets and Wouters (Reference Smets and Wouters2007). However, our estimated parameters on price and wage rigidity are slightly smaller than that in Smets and Wouters (Reference Smets and Wouters2007). The difference in estimation results comes from the data sample used, for example, in this study, we considered the full sample of the ZLB period with shadow rate rather than the nominal interest rate up to 2017. Another feature comes from the aggregator adopted in the price-setting problem; in our study we use the Dixit–Stiglitz aggregator while Smets and Wouters (Reference Smets and Wouters2007) uses the Kimball aggregator. For our full sample data (from 1947 to 2017) comparing to Smets and Wouters (Reference Smets and Wouters2007) (from 1966 to 2004), our sample data contain the more volatile inflation and wage periods, which results in a lower level price and wage rigidity levels. In addition, our estimated shocks are higher in magnitude comparing to that in Smets and Wouters (Reference Smets and Wouters2007), again this mainly results from our choice of sample data covering the financial crisis and aftermath periods, where we use the shadow policy rate which took negative values during these periods, that is, a highly volatile economy, transferred into a higher level of shocks.

5.1. Stage 2: The CB choice of rule

Given a steady-state inflation rate target, $\Pi$ , the Central Bank (CB) receives a mandate to implement the rule (29) and to maximize with respect to $\rho \in S$ a modified welfare criterion

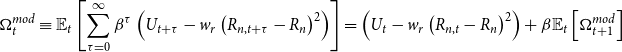(21) \begin{equation} \Omega _t^{mod} \equiv \mathbb{E}_t\left [ \sum _{\tau =0}^\infty \beta ^{\tau } \left(U_{t+\tau } - w_r \left(R_{n,t+\tau } - R_n \right)^2 \right)\right ]=\left(U_{t} - w_r \left(R_{n,t} - R_n \right)^2 \right)+ \beta \mathbb{E}_t \left [ \Omega _{t+1}^{mod} \right ] \end{equation}

in a zero-growth steady state with $g=0$ . To be consistent with our estimated model with $g\gt 0$ , we use a stationarized form:

(22) \begin{equation} \Omega _t^{mod} =\left(U_{t} - w_r \left(R_{n,t} - R_n \right)^2 \right)+ \beta (1+g)^{1-\sigma }\mathbb{E}_t \left [ \Omega _{t+1}^{mod} \right ] \end{equation}

Details of this stationary form are given in the Online Appendix B.1. One can think of this formulation as a mandate with a choice of penalty function $P=w_r \left(R_{n,t} - R_n \right)^2$ , penalizing the variance of the nominal interest rate with weight $w_r$ that is chosen at Stage 1 of the game.Footnote ¹⁵

Following Den Haan and Wind (Reference Den Haan and Wind2012), an alternative mandate that only penalizes the zero interest rate in an asymmetric fashion is $P=P(a_t)$ where the occasionally binding constraint is $a_t \equiv R_{n,t}-1 \ge 0$ with

(23) \begin{equation} P=P(a_t)= \frac{\exp (-w_r a_t)}{w_r} \end{equation}

and chooses a large $w_r$ . $P(a_t)$ then has the property

\begin{eqnarray*} \lim _{w_r \rightarrow \infty } P(a_t) &=& \infty \mbox{ for } a_t\lt 0\\ &=& 0 \mbox{ for } a_t\gt 0 \end{eqnarray*}

Thus, $P(a_t)$ enforces the ZLB approximately but with more accuracy as $w_r$ becomes large. Stages 2–1 then proceed as before, but we now confine ourselves to a large $w_r$ which will enable $\Pi$ to be close to unity.

Both the symmetric and asymmetric forms of a ZLB mandate result in a probability of hitting the ZLB

(24) \begin{equation} p=p(\Pi, \rho ^*(\Pi, w_r)) \end{equation}

where $\rho ^*(\Pi, w_r)$ is the optimized form of the rule given the steady-state target $\Pi$ and the weight on the interest rate volatility, $w_r$ .

5.2 Stage 1: Design of the mandate

The Government first chooses a per period probability $\bar{p}_{zlb}$ of the nominal interest rate hitting the ZLB (which defines the tightness of the ZLB constraint). Given this target low probability and given $w_r$ , $\Pi =\Pi ^*$ is chosen to satisfy

(25) \begin{equation} p(R_{n,t} \leq 1) \equiv p(\Pi ^*, \rho ^*(\Pi ^*, w_r)) \leq \bar{p}_{zlb} \end{equation}

This then achieves the ZLB constraint

(26) \begin{equation} R_{n,t} \geq 1 \mbox{ with probability } ( 1 - \bar{p}_{zlb}) \end{equation}

where $R_{n,t}$ is the nominal interest rate.

The leader then maximizes the actual household intertemporal welfare

(27) \begin{eqnarray} \Omega _t=\mathbb{E}_t\left [ \sum _{\tau =0}^\infty \beta ^{\tau } U_{t+\tau }\right ]= U_t+\beta (1+g)^{1-\sigma }\mathbb{E}_t \left [ \Omega _{t+1} \right ] \end{eqnarray}

with respect to $w_r$ .

This two-stage delegation game defines an equilibrium in choice variables $w_r^*$ , $\rho ^*$ , and $\Pi ^*$ given $\bar{p}_{zlb}$ that maximizes the actual household welfare subject to the ZLB constraint (26). It should be noted at this point that the Ramsey Optimum maximizes $\Omega _t$ given by (27) subject only to the constraints of the model, but with no ZLB concerns. As is standard in models such as ours it results in a zero net inflation ( $\Pi =1$ ).

5.3 Welfare-optimal simple rules

The concept and computation of optimized simple rules in an estimated model is central to this paper. We first make some general points before turning to the full delegation game and the results. We follow Schmitt-Grohe and Uribe (Reference Schmitt-Grohe and Uribe2007) quite closely, but with some important differences.

First recall the form of the estimated nominal interest rate rule:

(28) \begin{align} \log \left( \frac{R_{n,t}}{R_n}\right) & =\rho _r \log \left( \frac{R_{n,t-1}}{R_n}\right) +(1-\rho _r)\left(\theta _\pi \log \left(\frac{\Pi _{t}}{\Pi }\right) + \theta _y \log \left(\frac{Y_t}{Y}\right) + \theta _{dy} \log \left(\frac{Y_t}{Y_{t-1}}\right)\right) \nonumber \\ & \quad + \log (MPS_t) \end{align}

Unlike rules studied in the NK literature that respond to the output gap and therefore a fully flexible price version of the model, this rule makes no such demands on the central bank and rational agents; it only requires knowledge of the model itself and its deterministic steady state. Schmitt-Grohe and Uribe (Reference Schmitt-Grohe and Uribe2007) refer to such rules as “implementable.”

For optimal policy purposes, we remove the monetary policy shock $\log (MPS_t)$ and reparameterize the rule as

(29) \begin{equation} \log \left( \frac{R_{n,t}}{R_n}\right)=\rho _r \log \left( \frac{R_{n,t-1}}{R_n}\right) +\alpha _\pi \log \left(\frac{\Pi _{t}}{\Pi }\right) + \alpha _y \log \left(\frac{Y_t}{Y}\right) + \alpha _{dy} \log \left(\frac{Y_t}{Y_{t-1}}\right) \end{equation}

which allows for the possibility of an integral rule with $\rho _r=1$ . Let $\rho \equiv [ \rho _r, \alpha _\pi, \alpha _y, \alpha _{dy}]$ be the policy choice of feedback parameters that defines the exact form of the rule. We restrict ourselves to a class of possible rules that are locally saddle-path stable in the vicinity of the non-stochastic (deterministic) steady state. We denote this subset of rules by $S$ ; thus $\rho \in S$ .

Two forms of rule found in the literature are special cases of (29). First, put $\rho _r=1$ and $\alpha _{dy}=\alpha _{y}=0$ to give

(30) \begin{equation} \log \left( \frac{R_{n,t}}{R_n}\right)=\log \left( \frac{R_{n,t-1}}{R_n}\right) +\alpha _\pi \log \left(\frac{\Pi _{t}}{\Pi }\right) \end{equation}

Then integrating we arrive at

(31) \begin{equation} \log \left( \frac{R_{n,t}}{R_n}\right)=\alpha _\pi \log \left(\frac{P_{t}}{\bar{P}_t}\right) \end{equation}

which is a price level rule with the trend price-level given by $\frac{\bar{P}_t}{\bar{P}_{t-1}}=\Pi _t$ . The benefits of price-level targeting versus inflation targeting have been discussed in the literature review subsection of the Introduction. The intuition for the benefits of price-targeting is as follows: faced with an unexpected temporary rise in inflation, price-level stabilization commits the central bank to bring inflation below the target in subsequent periods. In contrast, with inflation targeting, the drift in the price level is accepted.Footnote ¹⁶

We begin by defining the intertemporal household welfare at time $t$ in recursive Bellman stationarized formFootnote ¹⁷ in a symmetric equilibrium form as:

(32) \begin{eqnarray} \Omega _t &=&U_t(C_t, C_{t-1}, H_t^s) +\beta _{g} \mathbb{E}_t \left [ \Omega _{t+1}\right ] \end{eqnarray}

where $\beta _{g}$ is a growth-adjusted discount factor defined by $\beta _g \equiv \beta (1+g)^{1-\sigma }$ . $\Omega _t$ is a function of policy, $R_{n,t}$ and all the estimated parameters in the model including those for the AR1 shocks processes. We take the latter dependence as given in what follows.

Given initial values for the predetermined variables, $\mathsf{Z}_0$ , optimal policy at time $t=0$ sets steady-state values for the nominal interest rate instrument $R_{n,t}$ , denoted by $R_n$ (which should be noted depends on the steady-state inflation target) and solves the maximization problem:

(33) \begin{align} \max _{\rho \in S} \Omega _0 ( \mathsf{Z}_0, R_n, \rho ) \end{align}

In fact the long-run (steady state) gross inflation rate target in the rule which we take to be $\Pi \ge 1$ (ruling out a liquidity trap) uniquely pins down the rest of the steady state so we can rewrite (33) as

(34) \begin{align} \max _{\rho \in S} \Omega _0 ( \mathsf{Z}_0, \Pi, \rho ) \end{align}

But this is a conditional and time-inconsistent criterion as the optimized rule at time $t$ becomes

(35) \begin{equation} \max _{\rho \in S} \Omega _t ( \mathsf{Z}_t, \Pi, \rho ) \Rightarrow \rho =\rho ( \mathsf{Z}_t, \Pi ) \end{equation}

At time $t=0$ optimal commitment is to the optimized rule and depends on $\mathsf{Z}_0$ . But with the mere passage of time reoptimization (in the absence of commitment) becomes a dependence on $\mathsf{Z}_t$ and this leads to an incentive to reoptimize (i.e., time inconsistency).

We remove one source of time-inconsistency by choosing a welfare conditional on the economy being at the steady state $\mathsf{Z}_t=\mathsf{Z}$ , which is exogenous and policy-invariant. But welfare is also conditional the steady-state inflation target, $\Pi$ , which is a policy choice leaving a well-known source of time-inconsistency arising from the incentive to engage in an inflation surprise.Footnote ¹⁸ The optimization problem then becomes

(36) \begin{equation} \max _{\rho \in S} \Omega ( \mathsf{Z}, \Pi, \rho ) \Rightarrow \rho =\rho ( \mathsf{Z}, \Pi ) \end{equation}

$\Omega$ is now time-invariant and since $\mathsf{Z}$ is policy-invariant, in what follows we simply write $\rho =\rho (\Pi )$ . Since the steady-state inflation target $\Pi$ is a policy choice chosen in the mandate a commitment to this particular value is the remaining source of time-inconsistency. Thus welfare at the steady state is maximized on average over all realizations of future shocks driving the exogenous stochastic processes given their deterministic steady states. The optimal rule $\rho ^*$ is computed using a second-order perturbation solution.Footnote ¹⁹ But there are no ZLB considerations for the nominal interest rate as yet. This leads us to the delegation game.

6.1. Stage 2 of the delegation game

At Stage 2, the central bank at time $t$ is instructed to maximize $\Omega _t^{mod}$ with respect to the feedback coefficients $\rho \equiv [ \rho _r, \alpha _\pi, \alpha _y, \alpha _{dy}]$ given the long-run inflation target $\Pi =\Pi ^*$ and the weight $w_r$ . Note that the CB takes the weight $w_r$ (presenting the objective function of the CB) and the steady state of inflation as given to find the optimized feedback rule. Therefore, in the exercise of the Stage 2, we simply run the optimized feedback (simple) rule on nominal interest rate for each given pair of $(w_r, \Pi )$ . The upper-left subplot of Fig. 2 shows the relationship between the ZLB probability for each value of the gross steady-state inflation rate. In particular, the probability of hitting the ZLB is a decreasing function in the level of the inflation target (see CGW, Ngo (Reference Ngo2018)), that is, given the same value of the weight $w_r$ , the probability of hitting the ZLB moves from the dashed down to the solid lines associating with an increasing of inflation from $1.00$ to $1.009$ (dashed-o and dashed-x lines express the inflation levels of $1.003$ – $1.006$ , respectively).

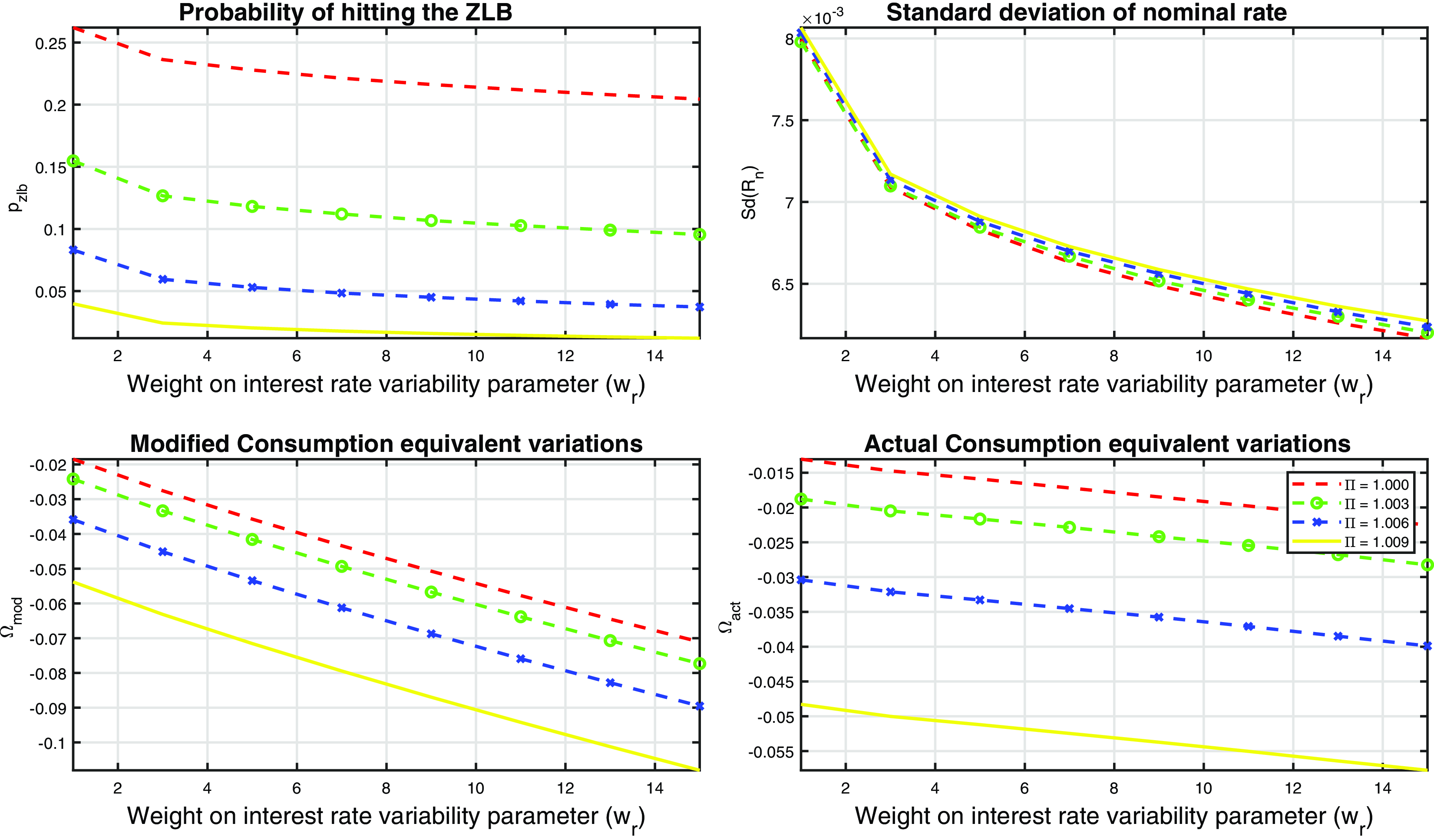
Figure 2. Plots of the probability of hitting the ZLB, the standard deviation of the instrument rate and the welfare criteria to the weight on interest rate variability parameter, $w_r$ (x-axis), and for different steady-state inflation levels (dashed to solid lines).

However, increasing the inflation target has two opposite effects on the probability of hitting the ZLB: the first is on the first moment by shifting the density function to the right reducing the probability of hitting ZLB; the second effect is on the second moment making the shape of the density function more fat-tailed. The upper-right subplot shows this second effect: namely that the standard deviation of the nominal rate is an increasing function of the inflation target thus increasing the probability of hitting ZLB. As shown from the upper-left subplot, the probability of hitting the ZLB is a decreasing function of the steady-state inflation, or the first effect dominates the second effect in this model.

From the lower-right subplot of Fig. 2, we can see that actual consumption equivalent variation (or actual welfare criterion) is a decreasing function in the inflation target. There are two remarks on this: first, if the ZLB is not taken into account, the optimal rate of gross inflation is one (or net inflation is zero) because there are only costs to inflation and no required shifting of the inflation rate; second, considering the set of all the steady-state inflation levels which satisfies the ZLB (the red arrow in Fig. 3), $\Pi ^* \geq \Pi ^{**} = 1.005$ , the policymaker chooses the target inflation of $\Pi ^{**} = 1.005$ with a given value of $w_r = 1$ and $\bar{p}_{zlb} = 0.103$ (approx. $0.1$ ). In other words, given a set of inflation target levels that satisfy the ZLB constraint, the lowest inflation target level is always chosen to maximize the actual welfare.

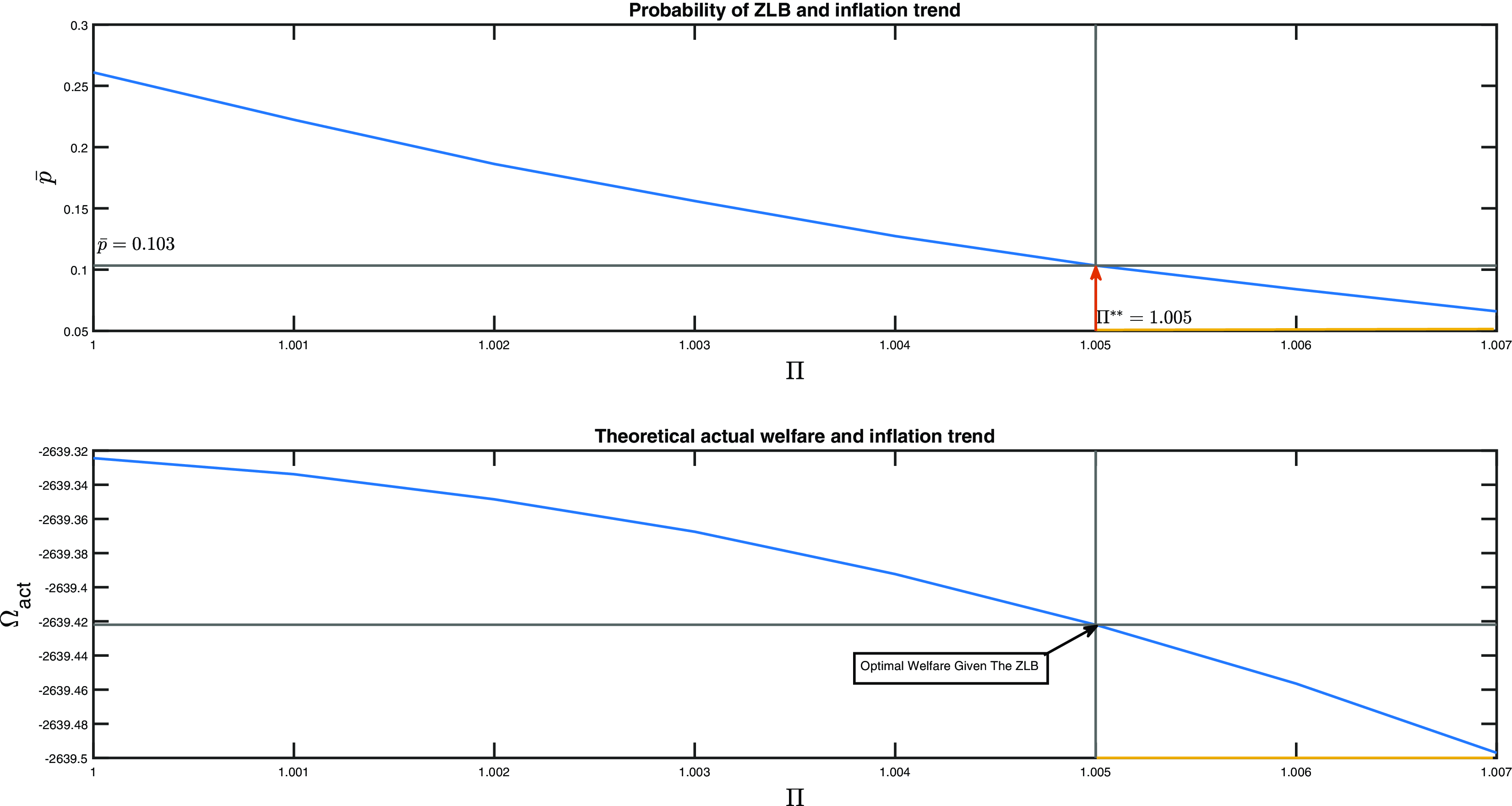
Figure 3. Figure illustrates the pick of optimal trend inflation from the set of steady-state inflation satisfying the ZLB constraint.

6.2 Stage 1: Imposing the ZLB and choice of $\Pi ^*$ and $w_r$

In this section, we impose the ZLB constraint (26) where the optimal inflation target is chosen to maximize the welfare for each value of $w_r$ as explained in the previous section.

In order to examine the model’s behavior under the binding ZLB constraint, we set the value of $\bar{p}_{zlb} = 0.05$ quarterly. Other values of $\bar{p}_{zlb}$ will be examined later. Fig. 4 shows the outcome for some variables under the binding ZLB constraint. The first plot of Fig. 4 shows the minimum values of steady-state inflation rate, $\Pi ^*$ , which satisfies (25) in Stage 2 with equality. As we argued above, any value of $\Pi$ which is larger than $\Pi ^*$ satisfies the ZLB constraint, but since welfare is a decreasing function of the inflation target values, the central bank will set the lowest inflation target satisfying the ZLB. In addition, with a higher level of weight attached on the variability of the nominal interest rate, the central bank is less aggressive in conducting its monetary policy in term of stabilizing the price; that is, we see a fall in feedback rule parameter on inflation. Finally, the equilibrium is represented by the red dotted point and is documented in Table 3. Under the ZLB constraint, the optimal weight imposed on the penalty term of ZLB mandate is relatively high at $w^*_r = 8$ .Footnote ²⁰

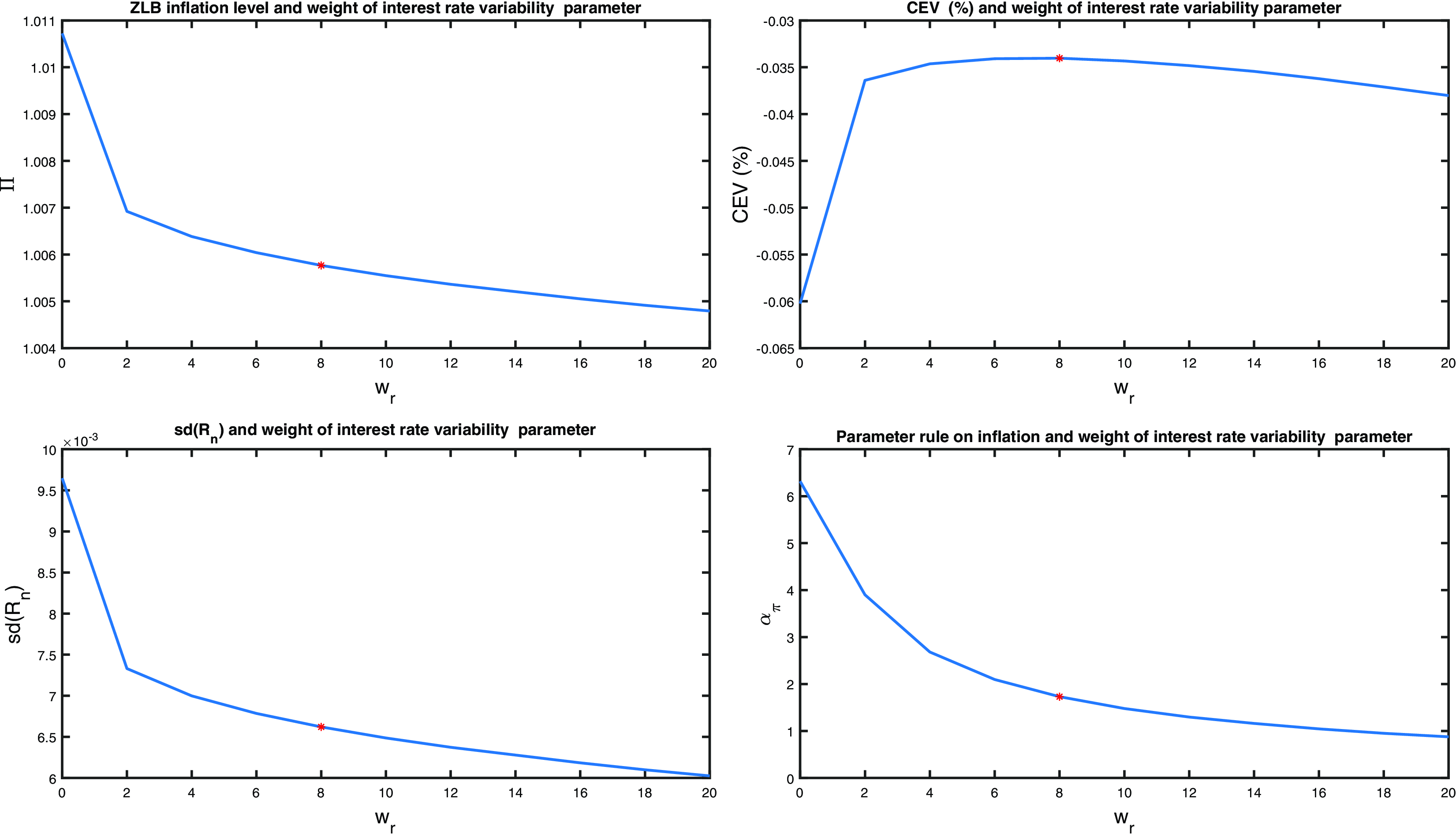
Figure 4. ZLB mandate with probability of the nominal interest rate hitting the ZLB constraint at 5%.

Table 3. Welfare stabilization from optimized rules compared with the estimated rule

Given the quarterly probability of hitting the ZLB at 1% (once quarter every 25 years), the optimal steady-state net inflation rate is then 3.7% annually. However, if we relax the ZLB constraint to an allowed probability of hitting the bound of 5%, the optimal steady-state net annual inflation is roughly 2.4%, a rate very close to the 2% inflation target of the Fed and other central banks. We also examine a probability 9.6% which is calibrated for sample data of the nominal interest rate used in the estimation exercise; we find for this probability a corresponding optimal inflation target of 1.6%. This optimal inflation rate is comparable to CGW who find that the optimal net annual inflation rate is around 1.5% in their benchmark model given their calibration of the unconditional probability of hitting the ZLB at 5% based on the post World War II (up to 2012) US experience.

The upper-right subplot in Fig. 4 expresses the behavior of the welfare gain given different values of the weight $w_r$ . Our choice of the quadratic penalty function on the policy rate, that is, the penalty on the volatility of the policy rate, results in a opening-down parabola shape, which gives us the exact value of $w^*_r$ where the associating optimal penalty function leads to a maximum social actual welfare. Similarly, the lower-right subplot gives us the optimal reaction of the central bank to the variation of inflation, that is, optimal feedback parameter on inflation in the Taylor rule, at the optimal $w_r$ . Finally, the lower-left subplot indicates the level of the policy rate’s volatility at $w^*_r$ .

6.3 Welfare gains from optimization and costs of the ZLB

In Table 3, we now assess the stabilization gains from optimized rules compared with the Ramsey policy using the household intertemporal welfare as the welfare criterion. By considering rules with and without the ZLB constraint its cost can also be quantified. We use the outcome of Ramsey optimum with zero net inflation and no ZLB constraint as the benchmark against which other regimes are measured. The subtables (A)–(E) focus on separate issues: in (A) the nominal interest rate rule is a component of the non-optimal estimated model and the welfare cost of this nonoptimality and that of the business cycle and is examined relative to a benchmark. In (B) this benchmark, the Ramsey optimum is reported along with the optimized rule at Stage 2 of the delegation game in the absence of a ZLB constraint and therefore no nominal interest rate penalty. In (C), the full equilibrium of the ZLB delegation game with a quadratic interest rate penalty function is reported. In (D), we compare this equilibrium with one where the quadratic penalty is replaced with the alternative asymmetric penalty as set out in Subsection 5.1. In (E), we restrict the mandate and interest rate setting rule ones with price-level targeting. Full details are as follows.

Subtable (A): Steady State Estimated Model. We first examine the steady-state welfare cost of the estimated model by setting the value of all the estimated shocks is equal to zero. The business cycle cost is relatively significant in our NK framework with a utility function that has habit and labor supply (see subtable No business cycle of Table 3).Footnote ²¹ Comparing the welfare outcome in the absence of shocks and with zero net inflation ( $\Pi = 1.0$ ), we see that our benchmark estimated rule without the business cycle results in a welfare gain of 0.456 CEV% (= (A1)–(A4)), or equivalently the welfare cost of business cycle is 0.456% CEV with zero net inflation. This is a much higher cost of the business cycle that found in Lucas (Reference Lucas1987) and (Reference Lucas2003).Footnote ²²

Subtable (A): Regimes of the Estimated Model. Given the estimated monetary policy shock of 0.33% (equals to the level value of 0.0033 in the Table 3) quarterly, welfare cost of the estimated inflation trend of 0.87% (3.5% annually) is approximately a 0.041% (= (A4)–(A5)) permanent reduction in consumption per quarter.Footnote ²³ Note that, in this exercise, we only compare the welfare cost of inflation levels between $\Pi = 1$ and $\Pi = 1.0087$ when there is a presence of monetary policy shock equaling to 0.33% for both inflation levels.

However, the higher empirical inflation trend results in a smaller probability of the nominal interest hitting the ZLB, that is, a zero steady-state inflation results in a per quarter probability of the ZLB incidence at 0.282 (approx 28 quarters in every 25 years), while a 3.5% of inflation trend induces a probability to 0.06 (or 6 quarters in every 25 years).

Sub-table (B): Optimized simple rule (OSR) without the ZLB constraint. Putting $w_r =0$ for these results, there is a significant welfare gain of the optimized rule compared to the estimated rule with the same steady-state inflation; that is, given a zero steady-state inflation welfare increases by 0.037 CEV% (= (B3)–(A3)). Moreover, the frequency of the nominal interest rate hitting the ZLB under optimized rule is close to that under the estimated one (0.30 to 0.28). There are two opposite impacts of these rules on the probability of the nominal interest rate hitting the ZLB. First, the optimized rule induces a lower volatility of the model compared to the estimated one, which makes the nominal interest rate also become less volatile (hence a smaller standard deviation). Second, it is the optimal value of the smoothing parameter $\rho _r$ , for example, under the estimated rule $\rho _r = 0.73$ which is much higher than that under the optimized rule ( $\rho _r = 0.0$ ). Hence, the higher the $\rho _r$ , the less volatile the nominal interest rate is. As a result, probability of the nominal interest rate hitting the ZLB becomes almost equal.

We also examine the performance of the original Taylor rule with its parameters calibrated from Taylor (Reference Taylor1993). Overall, there is a large welfare cost associated with the original Taylor rule of approximately 2.23–2.677 CEV% for the same target inflation rate and a very high probability of the nominal interest rate hitting the ZLB. This indicates that the inertia term on nominal interest rate, which is absent in the original Taylor rule, plays a crucial role in stabilizing the economy and lowering the possibility of the ZLB episode.

Finally in subtable (B), we compare outcomes with the Ramsey optimal policy (used as our benchmark about which the CEV is measured). As in Schmitt-Grohe and Uribe (Reference Schmitt-Grohe and Uribe2007), we find the optimized simple rule (OSR) with $\Pi =1$ but with no ZLB considerations, closely mimics this equilibrium.

Subtable (C): Optimized simple rule (OSR) with the ZLB constraint. To examine the welfare cost of the ZLB constraint, we now consider how changes in the frequency of nominal interest rate hitting the ZLB affect welfare by examining different values of $\bar{p}_{zlb}$ . We consider three different levels of $\bar{p}_{zlb}$ : 0.01 (one quarter every 25 years), 0.05 (five quarters every 25 years), and 0.096 (approx 10 quarters every 25 years). The 0.05 corresponds to the post-WWII experience of the USA used the calibration of CGW (up to 2012) while the latter considers the calibrated value of the data sample for estimation exercise which fully takes in account the ZLB period during the financial crisis and aftermath. Proceeding from the most to the least frequent of ZLB episodes, we then see the CEV cost rising from 0.024% ((C(3))) to 0.061% ((C(1))).

Our framework results in this welfare loss of ZLB episodes from two sources. First, the optimal steady-state inflation rate rises which, as discussed in Section 2.1, directly generates a welfare loss in the New Keynesian model through a higher price and wage dispersion. Second, the optimal mandate (the optimal determination of the penalty term in the delegated mandate, $w^*_r$ ) generates a suboptimal result from the social welfare point by constraining the use of the nominal interest rate for stabilization. It is worth noting that as the constraint becomes tighter, the optimized simple rule converges to a Taylor-type rule with a very high persistence.

Subtable (D): Optimized simple rule (OSR) with an asymmetric ZLB constraint. We next investigate the framework under an asymmetric formation of the ZLB mandate in the spirit of Den Haan and Wind (Reference Den Haan and Wind2012), which only penalizes the zero net interest rate in an asymmetric fashion. This type of central bank’s objective function implies that there is asymmetry under various economic structures which is fully taken into account by the central bank in conducting it monetary policy. The results in Table 3 are very similar in the symmetric and asymmetric cases suggesting that our ZLB mandate result is robust across these different forms of the ZLB mandate.

Subtable (E): Optimized price level rule. We next consider a special case of the Taylor-type simple rule (29):

(38) \begin{equation} \log \left( \frac{R_{n,t}}{R_n}\right)=\log \left( \frac{R_{n,t-1}}{R_n}\right) +\alpha _\pi \log \left(\frac{\Pi _{t}}{\Pi }\right) \end{equation}

Integrating the rule above gives:

(39) \begin{equation} \log \left( \frac{R_{n,t}}{R_n}\right)=\alpha _\pi \log \left(\frac{P_{t}}{\bar{P}_t}\right) \end{equation}

which is a price level rule with the trend price level given by $\frac{\bar{P}_t}{\bar{P}_{t-1}}=\Pi$ .

Giannoni (Reference Giannoni2014) argues that such simple price-level rule, comparing to the simple rule that responds to inflation, delivers superior results in several aspects of optimal monetary policy in the context of a NK model. First, price-level stabilization delivers outcomes that are closest to optimal. Second, such a policy has a robustness feature that delivers desirable outcomes even in the face of key types of model misspecification. Finally, price-level stabilization is more likely to result in a unique bounded equilibrium. Our results add a further advantage: the price-level rule closely mimics the general optimized rule with potential output feedbacks so price-level targeting helps to escape the ZLB. The intuition for the benefits of price targeting is as follows: faced with of an unexpected temporary rise in inflation price-level stabilization commits the Central Bank to bring inflation below the target in subsequent periods. In contrast, with inflation targeting, the drift in the price level is accepted.

Subtable E of the Table 3 represents the results of our mandate framework when the central bank is committed to price-level targeting rule. Overall, the price-level targeting rule replicates the mandate equilibrium. However, without a small trade-off between inflation and output activities, there is a higher welfare loss under the price-level targeting rule compared to the optimized simple rule.

6.4 A case for a 4% annual trend inflation target

In light of the recent consistent effective lower bound to central bank interest rates, the literature has also suggested that it is desirable to raise the inflation target to 4% to combat the ZLB on nominal interest rates (see for example Ball (Reference Ball2013)). In this section, we examines the impact of a 4% annual inflation trend scenario on the probability of the nominal interest rate hitting the ZLB in via our framework.

Results (C) and (D) from Table 3 suggest that if the gross quarterly inflation target is set at $\Pi ^*$ ranging from $1.0093$ to $1.00993$ which is equivalent to the net inflation ranging from $3.73$ % to $3.77$ % annually, the ZLB episode would happen at a very low frequency of 1 quarters every 25 years. A 4% (subtable (F) from Table 3) target would then bring the frequency down even further to $0.007$ if this is indeed what the policymaker aims for. Ascari and Ropele (Reference Ascari and Ropele2007) suggest that a case of 4% inflation trend would indeed give a leeway for the central bank under the effective lower bound on nominal rates episode, but will also significantly narrows the determinacy region for monetary policy rules. But this is not a concern for our optimized rules as parameters are chosen to lie within the determinacy region.

7.1 Mandates I–IV

Our mandate I is expressed in terms of the growth of output $\frac{Y_t}{Y_{t-1}}$ and gross inflation $\Pi _t$ relative to their steady states. The delegated mandate I now consists of:

(40) \begin{eqnarray} \Omega _t^{mod} \equiv - \mathbb{E}_t\left [ \sum _{\tau =0}^\infty \beta ^{\tau } \left(\left(\Pi _{t+\tau } - \Pi \right)^2 + w_{dy} \left(\frac{Y_{t+\tau }}{Y_{t+\tau -1}} - (1+g) \right)^2 + w_r \left(R_{n,t+\tau } - R_n \right)^2 \right) \right ] \end{eqnarray}

with a corresponding simple rule:

(41) \begin{equation} \log \left( \frac{R_{n,t}}{R_n}\right)=\rho _r \log \left( \frac{R_{n,t-1}}{R_n}\right) +\alpha _\pi \log \left(\frac{\Pi _{t}}{\Pi }\right) + \alpha _{dy} \log \left(\frac{Y_t}{Y_{t-1}}\right) \end{equation}

Our next mandate II is a special form of the price-level rule corresponding to strict inflation targeting mandate:

(42) \begin{eqnarray} \Omega _t^{mod} \equiv - \mathbb{E}_t\left [ \sum _{\tau =0}^\infty \beta ^{\tau } \left(\left(\Pi _{t+\tau } - \Pi \right)^2 + w_r \left(R_{n,t+\tau } - R_n \right)^2 \right) \right ] \end{eqnarray}

with a corresponding simple rule

(43) \begin{equation} \log \left( \frac{R_{n,t}}{R_n}\right)= \log \left( \frac{R_{n,t-1}}{R_n}\right) +\alpha _\pi \log \left(\frac{\Pi _{t}}{\Pi }\right) \end{equation}

Mandate III is expressed in terms of real wage growth $\frac{W_t}{W_{t-1}}$ and gross inflation $\Pi _t$ relative to their steady states. The delegated mandate now consists of:

(44) \begin{align} \Omega _t^{mod} \equiv - \mathbb{E}_t\left [ \sum _{\tau =0}^\infty \beta ^{\tau } \left(\left(\Pi _{t+\tau } - \Pi \right)^2 + w_{dw} \left(\frac{W_{t+\tau }}{W_{t+\tau -1}} -(1+g) \right)^2 + w_r \left(R_{n,t+\tau } - R_n \right)^2 \right) \right ] \end{align}

with a corresponding simple rule

(45) \begin{equation} \log \left( \frac{R_{n,t}}{R_n}\right)=\rho _r \log \left( \frac{R_{n,t-1}}{R_n}\right) +\alpha _\pi \log \left(\frac{\Pi _{t}}{\Pi }\right) + \alpha _{dw} \log \left(\frac{W_t}{W_{t-1}}\right) \end{equation}

Our final transparent delegated mandate IV is expressed in terms of employment growth $\frac{H_t^d}{H_{t-1}^d}$ and gross inflation $\Pi _t$ relative to their steady states. The delegated mandate now consists of:

(46) \begin{eqnarray} \Omega _t^{mod} \equiv - \mathbb{E}_t\left [ \sum _{\tau =0}^\infty \beta ^{\tau } \left(\left(\Pi _{t+\tau } - \Pi \right)^2 + w_{dh} \left(\frac{H^d_{t+\tau }}{H^d_{t+\tau -1}} -1 \right)^2 + w_r \left(R_{n,t+\tau } - R_n \right)^2 \right) \right ] \end{eqnarray}

Corresponding simple rule:

(47) \begin{equation} \log \left( \frac{R_{n,t}}{R_n}\right)=\rho _r \log \left( \frac{R_{n,t-1}}{R_n}\right) +\alpha _\pi \log \left(\frac{\Pi _{t}}{\Pi }\right) + \alpha _{dh} \log \left(\frac{H^d_t}{H^d_{t-1}}\right) \end{equation}

7.2 Numerical results for four mandates

Table 4 set out the numerical results for our four quadratic mandates. Again we set out the optimized rule for the central bank that, for each mandate, uses a quadratic loss function set out in Section 7.1 plus a interest rate penalty term. For each ZLB probability (the empirical $\bar{p}_{zlb}=0.096$ and the policy choices $\bar{p}_{zlb}=0.05, 0.01$ ), we report the welfare-optimal combination of the gross infaltion target $\Pi$ and penalty weights for each mandate using the actual household welfare as the criterion. The welfare-optimal mandate is then described by the choice of weights $(\Pi ^*, w_r^*, w_{dy}^*)$ for mandate I, $(\Pi ^*, w_r^*)$ for mandate II, $(\Pi ^*, w_r^*, w_{dw}^*)$ for mandate III and $(\Pi ^*, w_r^*, w_{dh}^*)$ for mandate IV. This choice depends on the tightness of the ZLB constraint, $\bar{p}_{zlb}$ for each case. In the table below, we report this welfare-optimal equilibrium for each mandate along with the actual welfare. The latter is also expressed in consumption-equivalen terms relative to the Ramsey optimum set out in Table 3. Full details of choosing the grids on the weights are presented in the appendices (Tables 3–6).

Table 4. Results for quadratic mandates

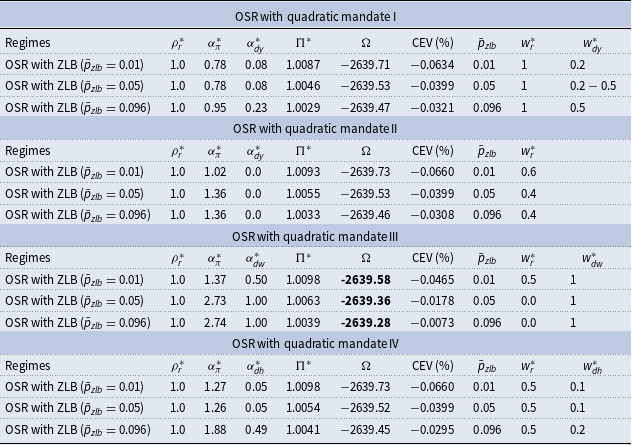
For these optimal mandates, we find that the weights attached to real economic activities based on a normalized unit quarterly inflation and quarterly rates of change of real variables are in the range 0.2–1.0. So we find some support for a dual mandate, but less than DKLN who find that simple loss functions should feature a weights of almost 3 for output growth.

The source of these differences in our framework lies in the model summarized in Section 3.6, the presence of the ZLB constraint and the coupling of the optimized appropriate interest rate rule with the loss function mandate. Considering the first of these, the Kimball aggregator in the original SW model (but not included in our set-up for reasons discussed in Section 3.6) adds a real rigidity to the model and providing a reason for designing policy to respond to the effects of shock on real variables such as output growth. The trend-inflation effect that is removed in Smets and Wouters (Reference Smets and Wouters2007), but present in our set-up, makes price and wage dispersion respond up to first order to shocks to price and wage inflation creating a reason for policy to react more to changes in the inflation rate for both the instrument rule and the comparable mandate. Another source of the difference is the nature of the delegation game. Whereas DKLN studies a Ramsey problem with the simple loss function as parsimonious approximations to social welfare, our paper investigates a simple interest-rate rule regime which matches the delegated a loss function. This limits the ability of the nominal interest rate to respond to the to any macroeconomic aggregate compared with the complex implied Ramsey rule and shifts the response of the optimized rule and the comparable mandate toward the inflation target.

However, for the best mandate III, which involve real wage growth targeting, the optimized interest rate rule responds strongly to this component. In doing so, it also reduces nominal wage dispersion resulting in a further welfare benefit.Footnote ²⁴ The associated optimal mandate then has a weight on wage growth close to that on inflation, that is, $w_{dw}^*=1$ .

7.3 General discussion

We have examined several forms of transparent loss function mandates that impose the ZLB constraint by penalizing the volatility of nominal interest rate. The results are striking in several respects. First, from the actual (representative household) welfare criterion, the integrated-ZLB conventional inflation-output optimal mandate I results in the highest welfare loss, while the nominal price and wage inflation targeting mandate IV lead to the lowest. The consumption equivalent differences are quite small and of the order 0.01%. But for all optimal mandates, there is a substantial welfare stabilization gain of the order of 0.1% compared with the outcome of the estimated rule. Generally in our NK model with labor supply and habit in the utility function and with price and wage stickiness both the welfare costs of the business cycle and the potential gains from stabilization policy are substantially greater than those found by Lucas (Reference Lucas2003) and in the RBC model without such distortions.

Second, in the quadratic mandates, the optimal weights attached to real economic activities (i.e., output or labor demand) are relatively small compared with the weight attached to quarterly price inflation. Only for mandate III targeting directly both nominal price and real wage growth do we find that the relative optimal weights attached to these targets are close to unity. This result contrasts with the strong support for the dual mandate found by DKLN where with a mandate with real activity output growth a weight of almost 3 is reported. The source of this difference has been discussed in Subsection 7.2.

Third, the associated optimized simple rules all converge to a price-level targeting rule, or at least to an interest-rate rule with the smoothing component on the nominal interest rate close to unity. Overall, the central bank reacts positively to output and labor demand, so a looser monetary policy corrects for a decline in these real economic variables. However, because the optimized weights in the loss function are relatively small, these real economic activity components also carry a small weight in the optimized simple rules.

Fourth, the formation of the optimal mandates has a little impact on the optimal steady-state inflation level. Overall, the optimal steady-state inflation does not vary across different formations of the mandate and the tightness level of the ZLB (the allowed probability of the nominal interest rate hitting the ZLB) is the main driving force on the optimal steady-state inflation. The allowed highest quarterly probability of 9.6% (approx 10 quarters every 25 years) corresponds to the data sample of the estimation exercise. We find that the optimal level of inflation trend rate is close to 1.2%, which is close to the result produced by CGW who calibrated the quarterly probability of 5% (approx 5 quarters every 25 years) which they note is consistent with the historical experience of the ZLB frequency for the USA from 1945 to 2012. In addition, with the calibrated quarterly probability of 5% in our study, we find the optimal inflation trend rate is close to the typical common-known 2% of most prominent central banks. There are two possible reasons for this discrepancy: first, our model is estimated by Bayesian methods with an empirical inflation trend and could claim to be more empirical; second, our choice of welfare function to design the mandate avoids any quadratic steady-state small-distortions approximation. We use a second-order perturbation approach that only assumes the variance of shocks are small which is confirmed in the estimation. We suspect that the first of these two reasons is the more important. Overall, the debate of optimal inflation target hinges entirely on the allowed probability of hitting ZLB.