1. Introduction
The goods market is undoubtedly characterized by a high degree of product differentiation, which enables firms to gain some monopoly power in the market. In pursuing such product differentiation to remain competitive, some overhead costs, such as those related to advertising, marketing, transaction, and R&D expenditures, are gradually increasing and being used by firms actively operating in the market. At the same time, in a monopolistically competitive market with free entry and exit, the number of firms in the market will change once a firm earns a positive profit or incurs a loss. It is the process of firms entering and exiting the market that allows the market to evolve and adjust along with the changing economic environment, which is also an essential feature of a monopolistically competitive market.
A growing strand of the literature, such as Jaimovich and Floetotto (Reference Jaimovich and Floetotto2008), Lewis (Reference Lewis2009) and Clementi and Palazzo (Reference Clementi and Palazzo2016), among others, examines how endogenous firm entry can contribute to understanding the business cycle. For example, Jaimovich and Floetotto (Reference Jaimovich and Floetotto2008) develop a general equilibrium framework, indicating that an imperfect competition model with endogenous firm entry can explain U.S. job-gains (losses) at a higher frequency. In her study, Lewis (Reference Lewis2009) shows that the number of firms varies over the business cycle and the correlation between aggregate output and net business formation is positive. Clementi and Palazzo (Reference Clementi and Palazzo2016) document that endogenous firm entry plays a major role in shaping aggregate dynamics. All these studies suggest that a model with endogenous firm entry implies a dynamic response of the extensive margin and is able to match the business cycle dynamics. In other words, the economy may be subjected to higher macroeconomic volatility when the market structure is characterized by endogenous firm entry.Footnote 1
To examine how the possibility of belief-driven cyclical fluctuations and equilibrium indeterminacy is related to the feature of endogenous firm entry and exit, a number of studies have devoted attention to discussing the issue in a monopolistic competition macroeconomic model with endogenous firm entry. For example, Chang et al. (Reference Chang, Hung and Huang2011) analyze the condition for local indeterminacy in a monopolistic competition model with such firm entry, finding that the condition for local indeterminacy depends on the degree of monopoly power. Chang et al. (Reference Chang, Lai and Chang2018) set up a monopolistic competition model featuring the returns to production specialization. Their analysis draws a distinction between production specialization and monopoly power, leading to the finding that the feature of production specialization plays an important role in governing local indeterminacy. Chen and Guo (Reference Chen and Guo2022) examine the interrelations between local indeterminacy and increasing returns to specialization within a monopolistic competition model. Their analysis shows that local indeterminacy can arise in the scenario where the increasing returns to production specialization are relatively strong.Footnote 2
A common feature of these monopolistic competition models is that a firm’s overhead costs are fixed.Footnote 3 However, the assumption of fixed overhead costs not only fails to reflect reality, but also results in an empirical tension. Accordingly, to provide an adequate explanation for variable overhead costs, overhead costs in this model are related to the number of firms (rather than being fixed), for which the correlation can be positive or negative. The introduction of this specification can be justified by discussing the following two reasons for its adoption.
First, in previous studies, Kim (Reference Kim2004) and Feng et al. (Reference Feng, Li and Swenson2017) document that, to make consumers aware of a brand and its product, a monopolistically competitive firm is inclined to enhance product differentiation through increasing advertising and marketing expenditures. In this case, in response to a rise in the number of firms in the market, an active firm will increase its overhead costs, such as those related to advertising and marketing expenditures, to create product differentiation. Prasad et al. (Reference Prasad, Sethi and Naik2009) set up an oligopoly model of advertising competition, showing that advertising expenditures will increase as the number of firms increases.
Second, Peretto (Reference Peretto1999) documents that R&D expenditures are one component of the firm’s total fixed costs and are negatively associated with the number of firms. A similar point is made by Peretto and Connolly (Reference Peretto and Connolly2007), who stress that, due to localized spillovers, it is less costly for new firms to innovate and enter the market with a larger number of firms. From the viewpoint of industry organization, Martin and Ottaviano (Reference Martin and Ottaviano2001) stress that industry clusters of economic activities are likely to reduce an incumbent firm’s overhead costs, such as those related to R&D, transaction and training costs, implying that overhead costs are negatively associated with the number of firms. To be specific, if the number of firms operating in the same industry is large, workers are more willing to enhance their professional skills and knowledge. This is because such professional skills are portable across firms in these industry clusters. In addition, when intermediate goods markets are located nearby, an incumbent firm can reduce its purchasing costs. As pointed out by Kamal and Sundaram (Reference Kamal and Sundaram2016), industry clusters facilitate knowledge transfer and the sharing of information on business norms and culture, and also reduce transaction costs related to these economic activities. This also implies that overhead costs will decrease as the number of firms increases. Furthermore, by using the Longitudinal Firm Trade Transactions Database, Kamal and Sundaram (Reference Kamal and Sundaram2016) show that overhead costs will decrease as the number of firms increases.
To reflect the importance of this industrial observation on overhead costs in the macroeconomic analysis, this paper contributes to the advancement of the literature on belief-driven business cycles by considering and analyzing the endogenous overhead costs. Compared with the existing literature on belief-driven business cycle models, this addition of endogenous overhead costs enables us to provide a further explanation as to how belief-driven business cycle fluctuations are related to the industry clusters by way of the mechanism resulting from the endogenous entry and exit of monopolistically competitive firms. The analysis is particularly important, since it is a new theoretical attempt to analyze industry clusters in relation to belief-driven business cycle fluctuations. Equipped with this feature, we show that the possibility of local indeterminacy is closely related to industry clusters. To be more precise, a higher degree of the spillover effect or a lower degree of the congestion effect tends to increase the likelihood of equilibrium indeterminacy.
The remainder of this paper is organized as follows. Section 2 sets up a monopolistically competitive model with firm entry and the endogeneity of overhead costs. Section 3 discusses the condition for equilibrium indeterminacy. Section 4 concludes the paper.
2. The model
We assume that the economy consists of two groups: firms and households. The production side of the economy consists of two sectors: the final good sector and the intermediate goods sector. The households derive utility from the consumption of the final good and disutility from labor supply.
2.1. Firms
Suppose that the final good
![]() $Y$
is produced through the use of a range of differentiated intermediate inputs
$Y$
is produced through the use of a range of differentiated intermediate inputs
![]() $y_{i}$
. Following Bénassy (Reference Benassy1996), final output is produced by a perfectly competitive firm with the following technology:Footnote 4
$y_{i}$
. Following Bénassy (Reference Benassy1996), final output is produced by a perfectly competitive firm with the following technology:Footnote 4
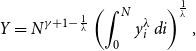 \begin{equation} Y=N^{\gamma +1-\frac{1}{\lambda }}\left(\int _{0}^{N}y_{i}^{\lambda }\,di\right)^{\frac{1}{\lambda }}, \end{equation}
\begin{equation} Y=N^{\gamma +1-\frac{1}{\lambda }}\left(\int _{0}^{N}y_{i}^{\lambda }\,di\right)^{\frac{1}{\lambda }}, \end{equation}
where
![]() $N$
is the number of intermediate goods, the parameter
$N$
is the number of intermediate goods, the parameter
![]() $\lambda \in (0,1)$
measures the degree of monopoly power, and the parameter
$\lambda \in (0,1)$
measures the degree of monopoly power, and the parameter
![]() $\gamma$
(
$\gamma$
(
![]() $\geq$
0) measures the extent of production specialization.
$\geq$
0) measures the extent of production specialization.
One point should be mentioned here. If all intermediate goods are produced in the same quantities, then the final output is expressed by
![]() $Y=N^{\gamma +1}y$
. It turns out that in the presence of production specialization (i.e.,
$Y=N^{\gamma +1}y$
. It turns out that in the presence of production specialization (i.e.,
![]() $\gamma \gt 0$
), a rise in the number of firms increases the production of final output more than proportionally, and this is referred to as the production-enhancing effect; see, example, Chang et al. (Reference Chang, Lai and Chang2018).
$\gamma \gt 0$
), a rise in the number of firms increases the production of final output more than proportionally, and this is referred to as the production-enhancing effect; see, example, Chang et al. (Reference Chang, Lai and Chang2018).
Assuming that the final good is the numéraire and that
![]() $p_{i}$
is the price of the
$p_{i}$
is the price of the
![]() $i$
th intermediate good, the profit-maximization problem for the final good firm can then be expressed as:
$i$
th intermediate good, the profit-maximization problem for the final good firm can then be expressed as:
Accordingly, the solution for the first-order condition leads to the following expression:
Eq. (2) is the inverse demand function for the
![]() $i$
th intermediate good, and the function is characterized by a price elasticity
$i$
th intermediate good, and the function is characterized by a price elasticity
![]() $1/(1-\lambda )$
. A larger
$1/(1-\lambda )$
. A larger
![]() $\lambda$
leads to a higher price elasticity, implying that the intermediate goods sector is more competitive. Therefore,
$\lambda$
leads to a higher price elasticity, implying that the intermediate goods sector is more competitive. Therefore,
![]() $\lambda$
measures the degree of monopoly power in the markets for intermediate products.
$\lambda$
measures the degree of monopoly power in the markets for intermediate products.
Intermediate good producers use capital and labor to produce a differentiated product, which they sell to the final good producers at the profit-maximizing price. The production technology for the
![]() $i$
th intermediate good producer is given by
$i$
th intermediate good producer is given by
where
![]() $A\gt 0$
is a constant technology parameter,
$A\gt 0$
is a constant technology parameter,
![]() $k_{i}$
and
$k_{i}$
and
![]() $h_{i}$
, respectively, denote the capital and labor hired by the
$h_{i}$
, respectively, denote the capital and labor hired by the
![]() $i$
th intermediate good producer,
$i$
th intermediate good producer,
![]() $1\gt a\gt 0$
is the share of capital, and
$1\gt a\gt 0$
is the share of capital, and
![]() ${\Gamma}$
is the overhead cost.
${\Gamma}$
is the overhead cost.
To highlight the difference between the literature on belief-driven fluctuations and this paper, the overhead cost in the model is expressed as follows:
This general form allows us to consider three distinctive scenarios for the overhead cost. The first scenario in association with
![]() $\sigma =0$
denotes the fixed effect. In this case, the overhead cost is fixed (i.e.,
$\sigma =0$
denotes the fixed effect. In this case, the overhead cost is fixed (i.e.,
![]() ${\Gamma} =f$
), and almost all existing studies including Chang et al. (Reference Chang, Hung and Huang2011), Pavlov and Weder (Reference Pavlov and Weder2012), Chang et al. (Reference Chang, Lai and Chang2018) and Chen and Guo (Reference Chen and Guo2022) adopt this specification. The second scenario in association with
${\Gamma} =f$
), and almost all existing studies including Chang et al. (Reference Chang, Hung and Huang2011), Pavlov and Weder (Reference Pavlov and Weder2012), Chang et al. (Reference Chang, Lai and Chang2018) and Chen and Guo (Reference Chen and Guo2022) adopt this specification. The second scenario in association with
![]() $\sigma \in (0,\infty )$
captures the congestion effect due to competitive differentiation, and denotes the viewpoint proposed by Kim (Reference Kim2004) and Feng et al. (Reference Feng, Li and Swenson2017): the greater the number of firms is associated with a higher overhead cost. The third scenario in association with
$\sigma \in (0,\infty )$
captures the congestion effect due to competitive differentiation, and denotes the viewpoint proposed by Kim (Reference Kim2004) and Feng et al. (Reference Feng, Li and Swenson2017): the greater the number of firms is associated with a higher overhead cost. The third scenario in association with
![]() $\sigma \in ({-}1,0)$
captures the spillover effect from industry clusters, and reveals the Peretto and Connolly (Reference Peretto and Connolly2007) and Kamal and Sundaram (Reference Kamal and Sundaram2016) viewpoint: the greater the number of firms is associated with a lower overhead cost.Footnote 5
$\sigma \in ({-}1,0)$
captures the spillover effect from industry clusters, and reveals the Peretto and Connolly (Reference Peretto and Connolly2007) and Kamal and Sundaram (Reference Kamal and Sundaram2016) viewpoint: the greater the number of firms is associated with a lower overhead cost.Footnote 5
Let
![]() $w$
and
$w$
and
![]() $r$
respectively denote the market wage and capital rental rate. Based on the inverse demand function reported in Eq. (2) and the production function reported in Eq. (3), the optimization problem of the
$r$
respectively denote the market wage and capital rental rate. Based on the inverse demand function reported in Eq. (2) and the production function reported in Eq. (3), the optimization problem of the
![]() $i$
th intermediate good producer can be expressed as
$i$
th intermediate good producer can be expressed as
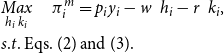 \begin{align} & \underset{h_{i}\,k_{i}}{Max}\quad \,\pi _{i}^{m}=p_{i}y_{i}-w\enspace h_{i}-r\enspace k_{i},\\& s.t.\ \text{Eqs. (2) and (3)}. \nonumber \end{align}
\begin{align} & \underset{h_{i}\,k_{i}}{Max}\quad \,\pi _{i}^{m}=p_{i}y_{i}-w\enspace h_{i}-r\enspace k_{i},\\& s.t.\ \text{Eqs. (2) and (3)}. \nonumber \end{align}
The first-order conditions with respect to
![]() $h_{i}$
and
$h_{i}$
and
![]() $k_{i}$
are
$k_{i}$
are
Then we obtain the profit of the
![]() $i$
th intermediate good producer by substituting Eqs. (6) and (7) into (5):
$i$
th intermediate good producer by substituting Eqs. (6) and (7) into (5):
The analysis is confined to a symmetric equilibrium under which
![]() $p_{i}=p, k_{i}=k, h_{i}=h$
, and
$p_{i}=p, k_{i}=k, h_{i}=h$
, and
![]() $y_{i}=y$
for all i. Let
$y_{i}=y$
for all i. Let
![]() $K$
and
$K$
and
![]() $H$
denote the aggregate capital stock and labor inputs, respectively. We then have:
$H$
denote the aggregate capital stock and labor inputs, respectively. We then have:
![]() $K=Nk$
and
$K=Nk$
and
![]() $H=Nh$
.
$H=Nh$
.
The zero-profit condition of perfect competition in the final good sector yields the following result:
Moreover, free entry guarantees zero profits for the intermediate goods sector. As a result, the production of each intermediate good and the number of firms in equilibrium are given by
 \begin{equation} N=\left(\frac{\left(1-\lambda \right)AK^{a}H^{1-a}}{f}\right)^{\frac{1}{1+\sigma }}. \end{equation}
\begin{equation} N=\left(\frac{\left(1-\lambda \right)AK^{a}H^{1-a}}{f}\right)^{\frac{1}{1+\sigma }}. \end{equation}
By inserting Eqs. (10) and (11) into (1), we can further obtain the aggregate production function as follows:
Based on Eq. (12), the following condition should be imposed to ensure that the externality is not sufficiently strong to generate sustained growth:Footnote 6
Condition NSG [the Nonsustained Growth Condition].
One point regarding Eqs. (10)–(12) should be stressed.Footnote 7 To compare the current endogenous overhead costs model with the fixed overhead costs model, we consider an extreme case of the fixed overhead costs scenario (i.e.,
![]() $\sigma =0$
). In this extreme case, we find that the individual firm’s output is fixed in equilibrium, and the number of firms is homogeneous of degree one in capital and labor. As a result, the aggregate production exhibits increasing returns to scale when
$\sigma =0$
). In this extreme case, we find that the individual firm’s output is fixed in equilibrium, and the number of firms is homogeneous of degree one in capital and labor. As a result, the aggregate production exhibits increasing returns to scale when
![]() $\gamma \gt 0$
. By contrast, this paper considers the feature of endogenous overhead costs. In this scenario, the equilibrium individual firm’s output is no longer fixed, and the number of firms is homogeneous of degree
$\gamma \gt 0$
. By contrast, this paper considers the feature of endogenous overhead costs. In this scenario, the equilibrium individual firm’s output is no longer fixed, and the number of firms is homogeneous of degree
![]() $1/(1+\sigma )$
in capital and labor. As a result, the aggregate production exhibits increasing returns to scale when
$1/(1+\sigma )$
in capital and labor. As a result, the aggregate production exhibits increasing returns to scale when
![]() $\gamma /(1+\sigma )\gt 0$
. Equipped with this knowledge, the analysis finds that the endogenously-determined overhead costs are closely related to the number of firms and therefore give rise to the congestion effect and the spillover effect, thereby governing the impact of the number of firms on aggregate production.
$\gamma /(1+\sigma )\gt 0$
. Equipped with this knowledge, the analysis finds that the endogenously-determined overhead costs are closely related to the number of firms and therefore give rise to the congestion effect and the spillover effect, thereby governing the impact of the number of firms on aggregate production.
2.2. Households
Consider an economy consisting of a unit measure of infinitely-lived households. The households maximize their lifetime utility
![]() $U$
by deriving utility from consumption
$U$
by deriving utility from consumption
![]() $C$
but incurring disutility from labor supply
$C$
but incurring disutility from labor supply
![]() $H$
. Thus, the lifetime utility of the households can be expressed as
$H$
. Thus, the lifetime utility of the households can be expressed as
where
![]() $\rho$
represents the rate of time preference,
$\rho$
represents the rate of time preference,
![]() $\zeta$
measures the disutility from labor supply, and
$\zeta$
measures the disutility from labor supply, and
![]() $t$
is the time index.
$t$
is the time index.
The households face the following budget constraint:Footnote 8
where
![]() ${\Pi} (=\int _{0}^{N}\pi _{i}^{m}\,di)$
refers to the aggregate profits transferred from intermediate good producers.
${\Pi} (=\int _{0}^{N}\pi _{i}^{m}\,di)$
refers to the aggregate profits transferred from intermediate good producers.
The households maximize the intertemporal utility reported in Eq. (13) subject to the budget constraint reported in Eq. (14). Performing the optimization problem leads to the following first-order conditions:
together with Eq. (14) and the transversality condition
![]() $\lim _{t\rightarrow \infty }\mu \,K\,e^{-\rho \,t}=0$
, where
$\lim _{t\rightarrow \infty }\mu \,K\,e^{-\rho \,t}=0$
, where
![]() $\mu$
is the shadow price of physical capital.
$\mu$
is the shadow price of physical capital.
Eq. (15) represents the households’ optimal consumption decision, Eq. (16) represents the households’ optimal decision regarding labor supply, and Eq. (17) is associated with the households’ optimal capital accumulation decision.
Combining Eq. (15) with (17) yields the familiar Keynes–Ramsey Rule:
In addition, inserting Eqs. (3), (9), (11) and (12) into (6) and (7) yields:
2.3. The Competitive Equilibrium
By substituting Eqs. (8), (19) and (20) into (14), we obtain the economy-wide resource constraint:
Based on Eqs. (12), (15), (16) and (19), we can solve for employment for the instantaneous relationship:
where
![]() $H_{K}=\frac{\partial H}{\partial K}=\frac{-a\left(1+\sigma +\gamma \right)H}{{\Omega} K}, H_{C}=\frac{\partial H}{\partial C}=\frac{\left(1+\sigma \right)H}{{\Omega} C}$
, and
$H_{K}=\frac{\partial H}{\partial K}=\frac{-a\left(1+\sigma +\gamma \right)H}{{\Omega} K}, H_{C}=\frac{\partial H}{\partial C}=\frac{\left(1+\sigma \right)H}{{\Omega} C}$
, and
![]() ${\Omega} =(1-a)(1+\sigma +\gamma )-(1+\sigma )$
.
${\Omega} =(1-a)(1+\sigma +\gamma )-(1+\sigma )$
.
3. Macroeconomic (in)stability
In this section we examine the condition of local indeterminacy. Substituting Eqs. (12) and (20) into (18) and (21), the dynamic system of the economy can be expressed as
 \begin{equation} \dot{C}=\left[a\lambda \left(\frac{1-\lambda }{f}\right)^{\frac{\gamma }{1+\sigma }}A^{\frac{1+\sigma +\gamma }{1+\sigma }}K^{\frac{a\left(1+\sigma +\gamma \right)}{1+\sigma }-1}H^{\frac{\left(1-a\right)\left(1+\sigma +\gamma \right)}{1+\sigma }}-\rho \right]C, \end{equation}
\begin{equation} \dot{C}=\left[a\lambda \left(\frac{1-\lambda }{f}\right)^{\frac{\gamma }{1+\sigma }}A^{\frac{1+\sigma +\gamma }{1+\sigma }}K^{\frac{a\left(1+\sigma +\gamma \right)}{1+\sigma }-1}H^{\frac{\left(1-a\right)\left(1+\sigma +\gamma \right)}{1+\sigma }}-\rho \right]C, \end{equation}
where
![]() $H$
is given by Eq. (22).
$H$
is given by Eq. (22).
Linearizing Eqs. (23) and (24) around the steady state
![]() $(\tilde{K},\tilde{C})$
yields:
$(\tilde{K},\tilde{C})$
yields:
 \begin{equation} \left[\begin{array}{l} \dot{K}\\ \dot{C} \end{array}\right] = \left[\begin{array}{l} J_{11}J_{12}\\ J_{21}J_{22} \end{array}\right] \left[\begin{array}{l} K-\tilde{K}\\ C-\tilde{C} \end{array}\right], \end{equation}
\begin{equation} \left[\begin{array}{l} \dot{K}\\ \dot{C} \end{array}\right] = \left[\begin{array}{l} J_{11}J_{12}\\ J_{21}J_{22} \end{array}\right] \left[\begin{array}{l} K-\tilde{K}\\ C-\tilde{C} \end{array}\right], \end{equation}
where
![]() $J_{11}=\frac{-a\left(1+\sigma +\gamma \right)\tilde{Y}}{{\Omega} \tilde{K}}, \ J_{12}=\frac{\left(1-a\right)\left(1+\sigma +\gamma \right)\tilde{Y}}{{\Omega} \tilde{C}}-1, \ J_{21}=\frac{-a\gamma \tilde{C}\tilde{Y}}{{\Omega} \tilde{K}^{2}}, \ J_{22}=\frac{a\left(1-a\right)\left(1+\sigma +\gamma \right)\tilde{Y}}{{\Omega} \tilde{K}}$
.
$J_{11}=\frac{-a\left(1+\sigma +\gamma \right)\tilde{Y}}{{\Omega} \tilde{K}}, \ J_{12}=\frac{\left(1-a\right)\left(1+\sigma +\gamma \right)\tilde{Y}}{{\Omega} \tilde{C}}-1, \ J_{21}=\frac{-a\gamma \tilde{C}\tilde{Y}}{{\Omega} \tilde{K}^{2}}, \ J_{22}=\frac{a\left(1-a\right)\left(1+\sigma +\gamma \right)\tilde{Y}}{{\Omega} \tilde{K}}$
.
Based on Eq. (25), we can infer the trace and determinant of the Jacobian:
Based on Condition NSG, we can derive the following expression:
![]() $(1-a)(1+\sigma +\gamma )\tilde{Y}-\gamma \tilde{C}=[(1-a)(1+\sigma )-a\gamma ]\tilde{Y}\gt 0$
. Thus, the numerator of
$(1-a)(1+\sigma +\gamma )\tilde{Y}-\gamma \tilde{C}=[(1-a)(1+\sigma )-a\gamma ]\tilde{Y}\gt 0$
. Thus, the numerator of
![]() $Det(J)$
is positive. As a result, we can infer that
$Det(J)$
is positive. As a result, we can infer that
![]() $Det(J)\gt 0$
(
$Det(J)\gt 0$
(
![]() $\lt 0$
) if and only if
$\lt 0$
) if and only if
![]() ${\Omega} =(1-a)(1+\sigma +\gamma )-(1+\sigma )\gt 0(\!\lt 0)$
.
${\Omega} =(1-a)(1+\sigma +\gamma )-(1+\sigma )\gt 0(\!\lt 0)$
.
3.1. The Condition for Equilibrium Indeterminacy
We are now in a position to examine how the feature of industry clusters affects the emergence of equilibrium indeterminacy. As addressed in the literature on dynamic rational expectations models, such as Liu and Turnovsky (Reference Liu and Turnovsky2005), Brito and Dixon (Reference Brito and Dixon2013), Lai and Chin (Reference Lai and Chin2013) and Chu et al. (Reference Chu, Liao, Liu and Zhang2021), there exists a unique perfect foresight equilibrium solution if the number of unstable roots equals the number of jump variables. Since
![]() $C$
is the only jump variable in this dynamic system, the steady-state equilibrium is locally determinate if only one of the roots is positive in the dynamic system, implying that the value of the determinant of the Jacobian is negative, that is,
$C$
is the only jump variable in this dynamic system, the steady-state equilibrium is locally determinate if only one of the roots is positive in the dynamic system, implying that the value of the determinant of the Jacobian is negative, that is,
![]() $Det(J)\lt 0$
. Based on this cognition, we formulate the following constraint for saddle-point stability:
$Det(J)\lt 0$
. Based on this cognition, we formulate the following constraint for saddle-point stability:
However, as argued by Benhabib and Farmer (Reference Benhabib and Farmer1994), Aguiar-Conraria and Wen (Reference Aguiar-Conraria and Wen2008), Guo and Harrison (Reference Guo and Harrison2010) and Lai et al. (Reference Lai, Chin and Chen2017), there exists a continuum of equilibrium paths converging to the steady state if the dynamic system has two negative roots, that is,
![]() $Det(J)\gt 0\gt Tr(J)$
. Therefore, the necessary and sufficient condition for our macroeconomy to exhibit local indeterminacy is that the two roots are both negative. Accordingly, we formulate the following constraint for equilibrium indeterminacy:
$Det(J)\gt 0\gt Tr(J)$
. Therefore, the necessary and sufficient condition for our macroeconomy to exhibit local indeterminacy is that the two roots are both negative. Accordingly, we formulate the following constraint for equilibrium indeterminacy:
The above discussion can be summarized by the following proposition:
Proposition 1. Under Condition NSG,
(i) the economy exhibits saddle-point stability if
 ${\Omega} =(1-a)(1+\sigma +\gamma )-(1+\sigma )\lt 0$
;
${\Omega} =(1-a)(1+\sigma +\gamma )-(1+\sigma )\lt 0$
;(ii) the economy displays local indeterminacy if
 ${\Omega} =(1-a)(1+\sigma +\gamma )-(1+\sigma )\gt 0$
.
${\Omega} =(1-a)(1+\sigma +\gamma )-(1+\sigma )\gt 0$
.
It is clear that the condition for equilibrium (in)stability is closely related to the capital share
![]() $a$
, the degree of production specialization
$a$
, the degree of production specialization
![]() $\gamma$
, and the extent of industry clusters
$\gamma$
, and the extent of industry clusters
![]() $\sigma$
. Therefore, we in turn examine how the possibility of local indeterminacy is related to each of these factors.
$\sigma$
. Therefore, we in turn examine how the possibility of local indeterminacy is related to each of these factors.
Two points related to the condition for local indeterminacy should be mentioned. First, in previous studies, Chang et al. (Reference Chang, Lai and Chang2018) and Chen and Guo (Reference Chen and Guo2022) focus on the situation where the feature of industry clusters is absent (i.e.,
![]() $\sigma =0$
). As a result, their analysis finds that local indeterminacy can occur, provided that the degree of production specialization is relatively large. Second, our analytical result further indicates that the condition for local indeterminacy crucially depends upon the effect of industry clusters, in addition to the returns to production specialization proposed in the existing literature.Footnote 9
$\sigma =0$
). As a result, their analysis finds that local indeterminacy can occur, provided that the degree of production specialization is relatively large. Second, our analytical result further indicates that the condition for local indeterminacy crucially depends upon the effect of industry clusters, in addition to the returns to production specialization proposed in the existing literature.Footnote 9
We first discuss the linkage between the possibility of equilibrium indeterminacy and the extent of production specialization
![]() $\gamma$
. Our intuitive explanation for this result is borrowed from Benhabib and Farmer (Reference Benhabib and Farmer1994). The condition for equilibrium indeterminacy requires that the equilibrium wage-hours locus be positively sloped and steeper than the labor supply curve. Accordingly, the condition for equilibrium indeterminacy can be expressed asFootnote 10
$\gamma$
. Our intuitive explanation for this result is borrowed from Benhabib and Farmer (Reference Benhabib and Farmer1994). The condition for equilibrium indeterminacy requires that the equilibrium wage-hours locus be positively sloped and steeper than the labor supply curve. Accordingly, the condition for equilibrium indeterminacy can be expressed asFootnote 10
When the households generate optimistic expectations as regards having a higher future return on capital, they will tend to increase their investment today, implying that the capital stock in the next period will increase. Given that labor and physical capital are complements in production, labor supply in the next period will increase, implying that more output will be produced, and this will in turn attract a greater number of firms to enter and produce in the market. In the presence of increasing returns to production specialization (i.e.,
![]() $\gamma \gt 0$
), a higher value of
$\gamma \gt 0$
), a higher value of
![]() $\gamma$
further reinforces the labor productivity via the production-enhancing effect, which is reflected by the factor
$\gamma$
further reinforces the labor productivity via the production-enhancing effect, which is reflected by the factor
![]() $\gamma$
on the left-hand side of Eq. (30). As a consequence, the economy is more susceptible to local indeterminacy when the magnitude of the production specialization is relatively large. In fact, this result is reminiscent of Chang et al. (Reference Chang, Lai and Chang2018) and Chen and Guo (Reference Chen and Guo2022).
$\gamma$
on the left-hand side of Eq. (30). As a consequence, the economy is more susceptible to local indeterminacy when the magnitude of the production specialization is relatively large. In fact, this result is reminiscent of Chang et al. (Reference Chang, Lai and Chang2018) and Chen and Guo (Reference Chen and Guo2022).
We then deal with how the possibility of equilibrium indeterminacy is related to the effect of industry clusters
![]() $\sigma$
. As described above, when the households become optimistic, the number of firms will increase in response. When more firms are being set up, an incumbent firm will raise its overhead costs due to the presence of the congestion effect (i.e.,
$\sigma$
. As described above, when the households become optimistic, the number of firms will increase in response. When more firms are being set up, an incumbent firm will raise its overhead costs due to the presence of the congestion effect (i.e.,
![]() $\sigma \gt 0$
), and this will restrain firms from entering and producing in the market. To be specific, a higher value of
$\sigma \gt 0$
), and this will restrain firms from entering and producing in the market. To be specific, a higher value of
![]() $\sigma$
reduces the contribution of the production-enhancing effect of entry and therefore weakens the labor productivity, which is reflected by the factor
$\sigma$
reduces the contribution of the production-enhancing effect of entry and therefore weakens the labor productivity, which is reflected by the factor
![]() $\sigma$
on the left-hand side of Eq. (30). As a result, the presence of the congestion effect mitigates the possibility of local indeterminacy. By contrast, in the presence of the spillover effect (i.e.,
$\sigma$
on the left-hand side of Eq. (30). As a result, the presence of the congestion effect mitigates the possibility of local indeterminacy. By contrast, in the presence of the spillover effect (i.e.,
![]() $\sigma \lt 0$
), an incumbent firm could reduce overhead costs when more firms are being set up, which may induce more firms to enter and produce in the market. As a result, the presence of the spillover effect enhances the contribution of the production-enhancing effect of entry and therefore reinforces the labor productivity, thereby increasing the possibility of local indeterminacy.
$\sigma \lt 0$
), an incumbent firm could reduce overhead costs when more firms are being set up, which may induce more firms to enter and produce in the market. As a result, the presence of the spillover effect enhances the contribution of the production-enhancing effect of entry and therefore reinforces the labor productivity, thereby increasing the possibility of local indeterminacy.
The above discussion can be summarized by the following proposition:
Proposition 2. In a monopolistic competition model with endogenous entry and industry clusters, a higher degree of production specialization and the spillover effect or a lower degree of the congestion effect tends to increase the possibility of the emergence of equilibrium indeterminacy.
3.2. Quantitative Analysis
To perform further quantitative analysis for the emergence of local indeterminacy, in this subsection we provide a quantitative assessment by resorting to a numerical analysis. Figure 1 is drawn to highlight the effect of both
![]() $\gamma$
and
$\gamma$
and
![]() $\sigma$
on the likelihood of equilibrium (in)determinacy. To compare our results with those of existing studies, the capital share is set to
$\sigma$
on the likelihood of equilibrium (in)determinacy. To compare our results with those of existing studies, the capital share is set to
![]() $a=0.3$
, a value used in Benhabib and Farmer (Reference Benhabib and Farmer1996), Chang and Lai (Reference Chang and Lai2017), Chen and Guo (Reference Chen and Guo2022) and many previous studies in the literature on belief-driven business cycles. We vary the extent of production specialization
$a=0.3$
, a value used in Benhabib and Farmer (Reference Benhabib and Farmer1996), Chang and Lai (Reference Chang and Lai2017), Chen and Guo (Reference Chen and Guo2022) and many previous studies in the literature on belief-driven business cycles. We vary the extent of production specialization
![]() $\gamma$
from 0 to 0.5 and the industrial cluster effect
$\gamma$
from 0 to 0.5 and the industrial cluster effect
![]() $\sigma$
from −1 to 1 to highlight its importance. As can be seen from Figure 1, the
$\sigma$
from −1 to 1 to highlight its importance. As can be seen from Figure 1, the
![]() $\sigma -\gamma$
space is divided into three areas. The white area at the lower right displays the region featured by saddle-point stability (i.e.,
$\sigma -\gamma$
space is divided into three areas. The white area at the lower right displays the region featured by saddle-point stability (i.e.,
![]() ${\Omega} \lt 0$
), the gray area at the upper middle depicts the region featured by equilibrium indeterminacy (i.e.,
${\Omega} \lt 0$
), the gray area at the upper middle depicts the region featured by equilibrium indeterminacy (i.e.,
![]() ${\Omega} \gt 0$
), while the white area at the upper left depicts the region that does not satisfy Condition NSG.
${\Omega} \gt 0$
), while the white area at the upper left depicts the region that does not satisfy Condition NSG.
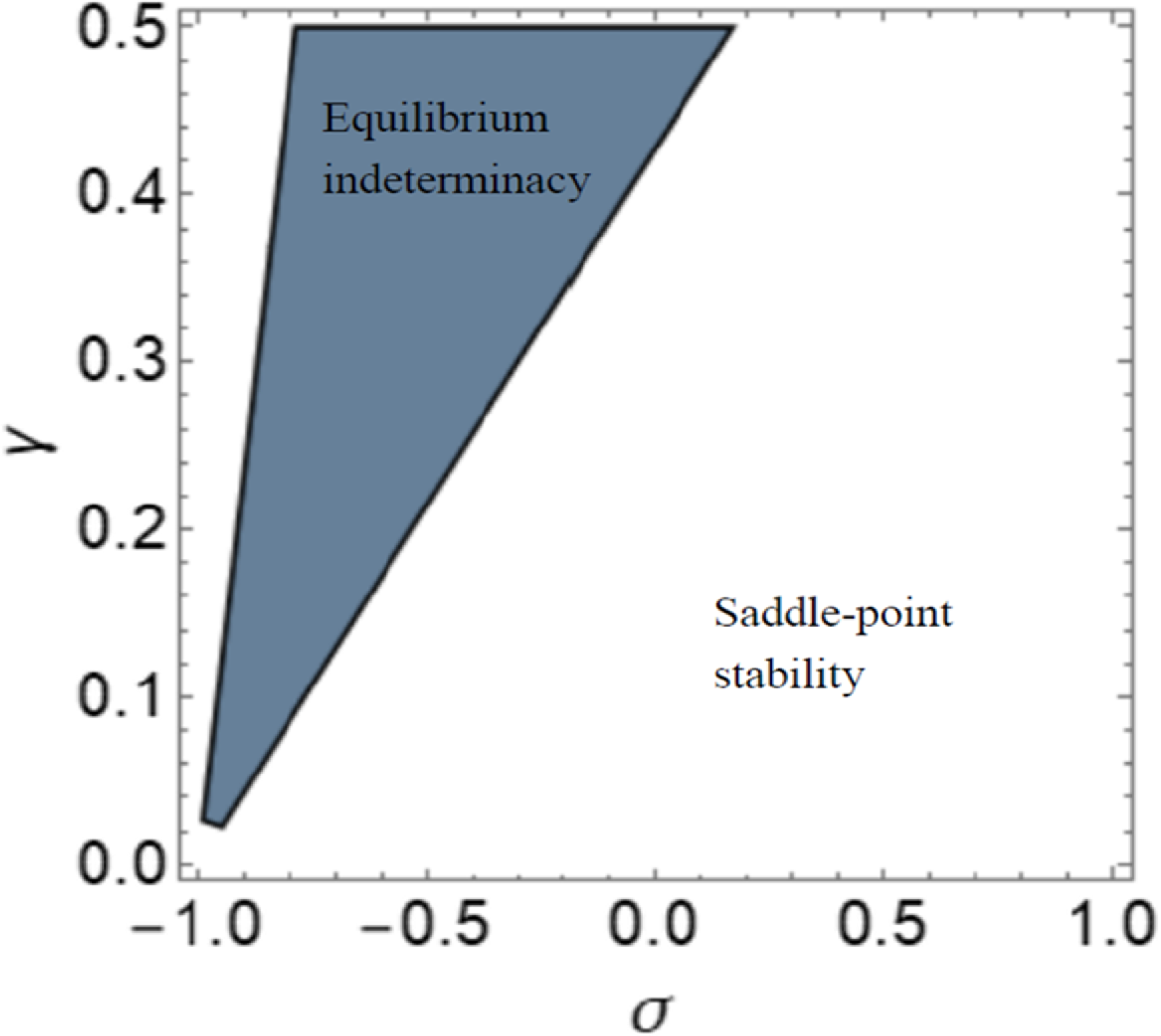
Figure 1. The saddle-point stability and equilibrium indeterminacy regions.
Three important results emerge from Figure 1. First, as indicated in Figure 1, a higher degree of production specialization matched with a higher degree of the spillover effect (a lower
![]() $\sigma$
) or a lower degree of the congestion effect tends to increase the likelihood of local indeterminacy. Second, as in Chang et al. (Reference Chang, Lai and Chang2018) and Chen and Guo (Reference Chen and Guo2022), in the absence of the industrial cluster effect (i.e.,
$\sigma$
) or a lower degree of the congestion effect tends to increase the likelihood of local indeterminacy. Second, as in Chang et al. (Reference Chang, Lai and Chang2018) and Chen and Guo (Reference Chen and Guo2022), in the absence of the industrial cluster effect (i.e.,
![]() $\sigma =0$
), local indeterminacy can occur, provided that the degree of production specialization is relatively large. To be more specific, the minimum degree of production specialization required for local indeterminacy is
$\sigma =0$
), local indeterminacy can occur, provided that the degree of production specialization is relatively large. To be more specific, the minimum degree of production specialization required for local indeterminacy is
![]() $\gamma _{\min }=0.429$
. Third, Kasahara and Rodrigue (Reference Kasahara and Rodrigue2008) indicate that the estimated degree of production specialization can be as high as 0.3. Given this parameter value, we have the minimum level of industry clusters required to satisfy the condition for local indeterminacy. To be more specific, the minimum level of industry clusters required for local indeterminacy is
$\gamma _{\min }=0.429$
. Third, Kasahara and Rodrigue (Reference Kasahara and Rodrigue2008) indicate that the estimated degree of production specialization can be as high as 0.3. Given this parameter value, we have the minimum level of industry clusters required to satisfy the condition for local indeterminacy. To be more specific, the minimum level of industry clusters required for local indeterminacy is
![]() $\sigma _{\min }=-0.3$
given that
$\sigma _{\min }=-0.3$
given that
![]() $\gamma =0.3$
.
$\gamma =0.3$
.
4. Conclusion
This paper develops a monopolistic competition macroeconomic model in which overhead costs are related to the number of firms. We then use the model to analyze the possibility of equilibrium indeterminacy and belief-driven cyclical fluctuations from the perspective of industrial organization. Two main findings emerge from the analysis. First, in the absence of an industrial cluster effect, equilibrium indeterminacy can occur, provided that the degree of production specialization is relatively large. Second, a higher degree of the spillover effect or a lower degree of the congestion effect tends to raise the likelihood of equilibrium indeterminacy.
Acknowledgment
I am deeply grateful to William A. Barnett (Editor), Roger Farmer (Co-Editor), and two anonymous referees for their insightful and constructive comments that have substantially improved the paper. Any shortcomings are, however, my responsibility.



