No CrossRef data available.
Published online by Cambridge University Press: 14 October 2024
We quantify the importance of endogenous human capital and of selection effects for counterfactual analysis of social security (SS) reforms. The literature typically performs these analyses by using structural models featuring exogenous productivity profiles. However, this approach faces two issues: (i) the estimation of productivity is subject to selection bias, and (ii) productivity is endogenous to the SS reforms. In this paper, we estimate a quantitative overlapping generations model featuring endogenous human capital accumulation using US data. First, we eliminate the SS and find a large positive effect on aggregate effective labor supply (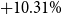 ${+}10.31\%$). Next, we build variants of this model to quantify the two issues (i) and (ii). We find that the endogeneity issue (ii) is quantitatively more important than the selection bias issue (i).
${+}10.31\%$). Next, we build variants of this model to quantify the two issues (i) and (ii). We find that the endogeneity issue (ii) is quantitatively more important than the selection bias issue (i).