No CrossRef data available.
Published online by Cambridge University Press: 29 September 2023
According to the real business cycle theory, business cycles mainly result from random exogenous shocks. In this paper, this argument is tested. I extend the Wald–Wolfowitz runs test under the assumption that a recession lasts for two periods at least and an expansion lasts for 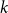 $k$ periods at least with k ≥ 2. I apply the extended runs test to the three two-valued data recession-expansion series generated by the National Bureau of Economic Research and the Center for Economic and Policy Research. The test results reject the null hypothesis that they are generated in a random way for any
$k$ periods at least with k ≥ 2. I apply the extended runs test to the three two-valued data recession-expansion series generated by the National Bureau of Economic Research and the Center for Economic and Policy Research. The test results reject the null hypothesis that they are generated in a random way for any 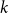 $k$ even at the 1% significance level.
$k$ even at the 1% significance level.