Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-24T14:05:37.996Z Has data issue: false hasContentIssue false
  • English
  • Français

Tuple lattice sieving

Part of: Geometry of numbers Computational number theory

Published online by Cambridge University Press:  26 August 2016

Shi Bai ,
Thijs Laarhoven  and
Damien Stehlé
Shi Bai
Affiliation:
ENS de Lyon, Laboratoire LIP, U. Lyon, CNRS, ENSL, INRIA, UCBL, Lyon, France email [email protected]
Thijs Laarhoven
Affiliation:
IBM Research, Rüschlikon, Switzerland email [email protected]
Damien Stehlé
Affiliation:
ENS de Lyon, Laboratoire LIP, U. Lyon, CNRS, ENSL, INRIA, UCBL, Lyon, France email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

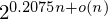Lattice sieving is asymptotically the fastest approach for solving the shortest vector problem (SVP) on Euclidean lattices. All known sieving algorithms for solving the SVP require space which (heuristically) grows as $2^{0.2075n+o(n)}$, where 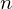$n$ is the lattice dimension. In high dimensions, the memory requirement becomes a limiting factor for running these algorithms, making them uncompetitive with enumeration algorithms, despite their superior asymptotic time complexity.

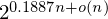We generalize sieving algorithms to solve SVP with less memory. We consider reductions of tuples of vectors rather than pairs of vectors as existing sieve algorithms do. For triples, we estimate that the space requirement scales as $2^{0.1887n+o(n)}$. The naive algorithm for this triple sieve runs in time 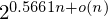$2^{0.5661n+o(n)}$. With appropriate filtering of pairs, we reduce the time complexity to 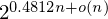$2^{0.4812n+o(n)}$ while keeping the same space complexity. We further analyze the effects of using larger tuples for reduction, and conjecture how this provides a continuous trade-off between the memory-intensive sieving and the asymptotically slower enumeration.

MSC classification

Primary: 11H06: Lattices and convex bodies
Secondary: 11Y16: Algorithms; complexity
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 19 , Special Issue A: Algorithmic Number Theory Symposium XII , 2016 , pp. 146 - 162
Copyright
© The Author(s) 2016 

References

Aggarwal, D., Dadush, D., Regev, O. and Stephens-Davidowitz, N., ‘Solving the shortest vector problem in 2 n time using discrete Gaussian sampling’, Proceedings of the STOC (ACM, 2015) 733–742.Google Scholar
Ajtai, M., Kumar, R. and Sivakumar, D., ‘A sieve algorithm for the shortest lattice vector problem’, Proceedings of the STOC (ACM, 2001) 601–610.Google Scholar
Albrecht, M., ‘DGS, an implementation of discrete Gaussians samplers over the integers’, available at https://github.com/malb/dgs.Google Scholar
Albrecht, M., Bai, S., Cadé, D., Pujol, X. and Stehlé, D., ‘FPLLL-4.0, a floating-point LLL implementation’, available at https://github.com/dstehle/fplll.Google Scholar
Becker, A., Ducas, L., Gama, N. and Laarhoven, T., ‘New directions in nearest neighbor searching with applications to lattice sieving’, Proceedings of the SODA (SIAM, 2016) 10–24.Google Scholar
SVP Challenge. ‘Svp challenge generator’, available at http://latticechallenge.org/svp-challenge.Google Scholar
Chen, Y. and Nguyen, P. Q., ‘BKZ 2.0: better lattice security estimates’, Proceedings of the ASIACRYPT , Lecture Notes in Computer Science 7073 (Springer, 2011) 1–20.Google Scholar
Fitzpatrick, R., Bischof, C., Buchmann, J., Dagdelen, Ö, Göpfert, F., Mariano, A. and Yang, B.-Y., ‘Tuning GaussSieve for speed’, Proceedings of the LATINCRYPT , Lecture Notes in Computer Science 9230 (Springer, 2015) 288–305.Google Scholar
Gama, N., Nguyen, P. Q. and Regev, O., ‘Lattice enumeration using extreme pruning’, Proceedings of the EUROCRYPT , Lecture Notes in Computer Science 6110 (Springer, 2010) 257–278.Google Scholar
Gentry, C., Peikert, C. and Vaikuntanathan, V., ‘Trapdoors for hard lattices and new cryptographic constructions’, Proceedings of the STOC (ACM, 2008) 197–206.Google Scholar
Hanrot, G., Pujol, X. and Stehlé, D., ‘Algorithms for the shortest and closest lattice vector problems’, IWCC , Lecture Notes in Computer Science 6639 (Springer, 2011) 159–190.Google Scholar
Hanrot, G. and Stehlé, D., ‘Improved analysis of Kannan’s shortest lattice vector algorithm’, Proceedings of CRYPTO , Lecture Notes in Computer Science 4622 (Springer, 2007) 170–186.Google Scholar
Hanrot, G. and Stehlé, D., ‘Worst-case Hermite–Korkine–Zolotarev reduced lattice bases’, CoRR, Preprint, 2008, arXiv:0801.3331.Google Scholar
Hoffstein, J., Pipher, J. and Silverman, J. H., ‘NTRU: a ring based public key cryptosystem’, Proceedings of the ANTS , Lecture Notes in Computer Science 1423 (Springer, 1998) 267–288.Google Scholar
Inverse Symbolic Calculator, available at https://isc.carma.newcastle.edu.au/index.Google Scholar
Kannan, R., ‘Improved algorithms for integer programming and related lattice problems’, Proceedings of the STOC (ACM, 1983) 99–108.Google Scholar
Laarhoven, T., ‘Sieving for shortest vectors in lattices using angular locality-sensitive hashing’, Proceedings of the CRYPTO , Lecture Notes in Computer Science 9215 (Springer, 2015) 3–22.Google Scholar
Laarhoven, T., Mosca, M. and van de Pol, J., ‘Finding shortest lattice vectors faster using quantum search’, DCC 77 (2015) no. 2–3, 375–400.Google Scholar
Micciancio, D. and Regev, O., ‘Lattice-based cryptography’, Post-Quantum Cryptography (eds Bernstein, D. J., Buchmann, J. and Dahmen, E.; Springer, 2009) 147–191.Google Scholar
Micciancio, D. and Voulgaris, P., ‘Faster exponential time algorithms for the shortest vector problem’, Proceedings of SODA (ACM, 2010).Google Scholar
Nguyen, P. Q. and Stehlé, D., ‘Low-dimensional lattice basis reduction revisited’, ACM Trans. Algorithms 5 (2009) no. 4, Article 46.Google Scholar
Nguyen, P. Q. and Vidick, T., ‘Sieve algorithms for the shortest vector problem are practical’, J. Math. Cryptol. 2 (2008) no. 2.Google Scholar
Pujol, X. and Stehlé, D., ‘Solving the shortest lattice vector problem in time $2^{2.465n}$ ’, Cryptology ePrint Archive, Report 2009/605, 2009, http://eprint.iacr.org/2009/605.Google Scholar
Regev, O., ‘Lecture notes of Lattices in Computer Science’, taught at the Computer Science Tel Aviv University, available at http://www.cims.nyu.edu/∼regev/teaching/lattices_fall_2004/index.html.Google Scholar
Semaev, I., ‘A 3-dimensional lattice reduction algorithm’, Proceedings of the CALC , Lecture Notes in Computer Science 2146 (Springer, 2001) 181–193.Google Scholar
Tammela, P. P., ‘On the reduction theory of positive quadratic forms’, Sov. Math. Dokl. 14 (1973) 651–655.Google Scholar
The Sage Developers, ‘Sage mathematics software (Version 6.8)’, 2015, http://www.sagemath.org.Google Scholar
Wolfram Research, Inc., Mathematica (version 10.3), 2015.Google Scholar