Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-25T13:01:25.445Z Has data issue: false hasContentIssue false
  • English
  • Français

Squarefree values of trinomial discriminants

Part of: Algebraic number theory: global fields Multiplicative number theory

Published online by Cambridge University Press:  01 January 2015

David W. Boyd ,
Greg Martin  and
Mark Thom
David W. Boyd
Affiliation:
Department of Mathematics, University of British Columbia, Room 121, 1984 Mathematics Road, Vancouver, BC, Canada V6T 1Z2 email [email protected]
Greg Martin
Affiliation:
Department of Mathematics, University of British Columbia, Room 121, 1984 Mathematics Road, Vancouver, BC, Canada V6T 1Z2 email [email protected]
Mark Thom
Affiliation:
Department of Mathematics & Computer Science, University of Lethbridge, C526 University Hall, 4401 University Drive, Lethbridge, AB, Canada T1K 3M4 email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

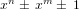The discriminant of a trinomial of the form $x^{n}\pm \,x^{m}\pm \,1$ has the form 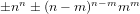$\pm n^{n}\pm (n-m)^{n-m}m^{m}$ if $n$ and 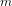$m$ are relatively prime. We investigate when these discriminants have nontrivial square factors. We explain various unlikely-seeming parametric families of square factors of these discriminant values: for example, when $n$ is congruent to 2 (mod 6) we have that 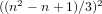$((n^{2}-n+1)/3)^{2}$ always divides 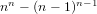$n^{n}-(n-1)^{n-1}$. In addition, we discover many other square factors of these discriminants that do not fit into these parametric families. The set of primes whose squares can divide these sporadic values as $n$ varies seems to be independent of 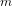$m$, and this set can be seen as a generalization of the Wieferich primes, those primes $p$ such that 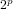$2^{p}$ is congruent to 2 (mod 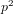$p^{2}$). We provide heuristics for the density of these sporadic primes and the density of squarefree values of these trinomial discriminants.

MSC classification

Primary: 11N32: Primes represented by polynomials; other multiplicative structure of polynomial values 11N25: Distribution of integers with specified multiplicative constraints 11N05: Distribution of primes
Secondary: 11R29: Class numbers, class groups, discriminants
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 18 , Issue 1 , 2015 , pp. 148 - 169
Copyright
© The Author(s) 2015 

References

Dorais, F. G. and Klyve, D., ‘A Wieferich prime search up to 6. 7 × 1015 ’, J. Integer Seq. 14 (2011) no. 9, #11.9.2 (14 pp).Google Scholar
Esmonde, J. and Murty, R., Problems in algebraic number theory , 2nd edn (Springer, New York, 2005).Google Scholar
Feller, W., An introduction to probability theory and its applications , 3rd edn (John Wiley & Sons, New York, 1968).Google Scholar
Gel’fand, I. M., Kapranov, M. M. and Zelevinsky, A. V., Discriminants, resultants, and multidimensional determinants , Mathematics: Theory & Applications (Birkhäuser, Boston, 1994).CrossRefGoogle Scholar
Heath–Brown, D. R., ‘An estimate for Heilbronn’s exponential sum’, Analytic number theory: Proceedings of a conference in honor of Heini Halberstam (Birkhaüser, Boston, 1996) 451–463.Google Scholar
Helou, C., ‘Cauchy–Mirimanoff polynomials’, C. R. Math. Rep. Acad. Sci. Canada 19 (1997) no. 2, 51–57.Google Scholar
Kedlaya, K., ‘A construction of polynomials with squarefree discriminants’, Proc. Amer. Math. Soc. 140 (2012) no. 9, 3025–3033.Google Scholar
Lagarias, J., Problem 99:10 in ‘Western number theory problems, 16 & 19 Dec 1999’, Asilomar, CA (ed. G. Myerson), http://www.math.colostate.edu/∼achter/wntc/problems/problems2000.pdf.Google Scholar
Lang, S., ‘Old and new conjectured Diophantine inequalities’, Bull. Amer. Math. Soc. (N.S.) 23 (1990) no. 1, 37–75.Google Scholar
Ljunggren, W., ‘On the irreducibility of certain trinomials and quadrinomials’, Math. Scand. 8 (1960) 65–70.CrossRefGoogle Scholar
Mirimanoff, D., ‘Sur l’équation (x + 1 l ) − x l − 1 = 0’, Nouv. Ann. Math. 3 (1903) 385–397.Google Scholar
Mit’kin, D. A., ‘An estimate for the number of roots of some comparisons by the Stepanov method’, Mat. Zametki 51 (1992) no. 6, 52–58; 157 (Russian); translation in Math. Notes 51 (1992), no. 5–6, 565–570.Google Scholar
Osada, H., ‘The Galois groups of the polynomials X n + a X l + b ’, J. Number Theory 25 (1987) no. 2, 230–238.Google Scholar
Ribenboim, P., 13 lectures on Fermat’s last theorem (Springer, New York, 1979).Google Scholar
Ribenboim, P., The new book of prime number records (Springer, New York, 1996).Google Scholar
Silverman, J. H., ‘Wieferich’s criterion and the a b c-conjecture’, J. Number Theory 30 (1988) 226–237.Google Scholar
Slatkevičius, R., PrimeGrid web site, http://www.primegrid.com; statistics on Wieferich prime search, http://prpnet.mine.nu:13000.Google Scholar
Stewart, C. L. and Tijdeman, R., ‘On the Oesterlé–Masser conjecture’, Monatsh. Math. 102 (1986) no. 3, 251–257.Google Scholar
Swan, R., ‘Factorization of polynomials over finite fields’, Pacific J. Math. 12 (1962) 1099–1106.CrossRefGoogle Scholar
Thom, M., ‘Square-free trinomial discriminants’, M.Sc. essay, University of British Columbia, Vancouver, 2011 (26 pp).Google Scholar
Tzermias, P., ‘On Cauchy–Liouville–Mirimanoff polynomials’, Canad. Math. Bull. 50 (2007) no. 2, 313–320.Google Scholar