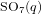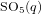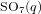Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Goodwin, Simon M.
Le, Tung
and
Magaard, Kay
2017.
The generic character table of a Sylow p-subgroup of a finite Chevalley group of type D4.
Communications in Algebra,
Vol. 45,
Issue. 12,
p.
5158.
Paolini, Alessandro
2018.
On the decomposition numbers ofSO8+(2f).
Journal of Pure and Applied Algebra,
Vol. 222,
Issue. 12,
p.
3982.
Le, Tung
Magaard, Kay
and
Paolini, Alessandro
2019.
The irreducible characters of the Sylow p-subgroups of the Chevalley groups D6(p) and E6(p).
Journal of Symbolic Computation,
Vol. 95,
Issue. ,
p.
68.