Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T13:28:52.661Z Has data issue: false hasContentIssue false
  • English
  • Français

On the distribution of Atkin and Elkies primes for reductions of elliptic curves on average

Part of: Arithmetic algebraic geometry Computational number theory Exponential sums and character sums

Published online by Cambridge University Press:  01 April 2015

Igor E. Shparlinski  and
Andrew V. Sutherland
Igor E. Shparlinski
Affiliation:
Department of Pure Mathematics, University of New South Wales, Sydney NSW 2052, Australia email [email protected]
Andrew V. Sutherland
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

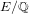For an elliptic curve $E/\mathbb{Q}$ without complex multiplication we study the distribution of Atkin and Elkies primes 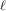$\ell$, on average, over all good reductions of 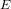$E$ modulo primes $p$. We show that, under the generalized Riemann hypothesis, for almost all primes $p$ there are enough small Elkies primes 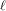$\ell$ to ensure that the Schoof–Elkies–Atkin point-counting algorithm runs in 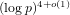$(\log p)^{4+o(1)}$ expected time.

MSC classification

Primary: 11Y16: Algorithms; complexity
Secondary: 11G05: Elliptic curves over global fields 11G07: Elliptic curves over local fields 11L40: Estimates on character sums
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 18 , Issue 1 , 2015 , pp. 308 - 322
Copyright
© The Author(s) 2015 

References

Avanzi, R., Cohen, H., Doche, C., Frey, G., Lange, T., Nguyen, K. and Vercauteren, F., Elliptic and hyperelliptic curve cryptography: theory and practice (CRC Press, Boca Raton, FL, 2005).Google Scholar
Bröker, R., Lauter, K. and Sutherland, A. V., ‘Modular polynomials via isogeny volcanoes’, Math. Comp. 81 (2011) 1201–1231.Google Scholar
Bröker, R. and Sutherland, A. V., ‘An explicit height bound for the classical modular polynomial’, Ramanujan J. 22 (2010) 293–313.Google Scholar
Cojocaru, A. C. and David, C., ‘Frobenius fields for elliptic curves’, Amer. J. Math. 130 (2008) 1535–1560.Google Scholar
David, C. and Wu, J., ‘Almost-prime orders of elliptic curves over finite fields’, Forum Math. 24 (2012) 99–120.Google Scholar
David, C. and Wu, J., ‘Pseudoprime reductions of elliptic curves’, Canad. J. Math. 64 (2012) 81–101.Google Scholar
Elkies, N., ‘Distribution of supersingular primes’, Astérisque 198–200 (1991) 127–132.Google Scholar
Elkies, N., ‘Elliptic and modular curves over finite fields and related computational issues’, Computational perspectives on number theory , Studies in Advanced Mathematics 7 (eds Buell, D. A. and Teitelbaum, J. T.; American Mathematical Society, Providence, RI, 1998) 21–76.Google Scholar
Fürer, M., ‘Faster integer multiplication’, SIAM J. Comput. 39 (2009) 979–1005.Google Scholar
Galbraith, S., Mathematics of public key cryptography (Cambridge University Press, Cambridge, 2012).Google Scholar
von zur Gathen, J. and Gerhard, J., Modern computer algebra , 2nd edn (Cambridge University Press, Cambridge, 2003).Google Scholar
Harvey, D., ‘Counting points on hyperelliptic curves in average polynomial time’, Ann. of Math. (2) 179 (2014) 783–803.Google Scholar
Harvey, D., ‘Computing zeta functions of arithmetic schemes’, Preprint, 2014, arXiv:1402.3439.Google Scholar
Harvey, D., van der Hoeven, J. and Lecerf, G., ‘Even faster integer multiplication’, Preprint, 2014, arXiv:1407.3360.Google Scholar
Harvey, D. and Sutherland, A., ‘Computing Hasse–Witt matrices of hyperelliptic curves in average polynomial time’, LMS J. Comput. Math. 17 (2014) 257–273 (Proceedings of the Algorithmic Number Theory Symposium (ANTS XI), 2014).Google Scholar
Harvey, D. and Sutherland, A., ‘Computing Hasse–Witt matrices of hyperelliptic curves in average polynomial time, II’, Preprint, 2014, arXiv:1410.5222.Google Scholar
Lagarias, J. C. and Odlyzko, A. M., ‘Effective versions of the Chebotarev density theorem’, Algebraic number fields (Academic Press, New York, 1977) 409–464.Google Scholar
Lamzouri, Y., Li, X. and Soundararajan, K., ‘Conditional bounds for the least quadratic non-residue and related problems’, Math. Comp. to appear.Google Scholar
Montgomery, H. L., Topics in multiplicative number theory , Lecture Notes in Mathematics 227 (Springer, Berlin, 1971).Google Scholar
Rabin, M. O., ‘Probabilistic algorithms in finite fields’, SIAM J. Comput. 9 (1980) 273–280.Google Scholar
Rubin, K. and Silverberg, A., ‘Choosing the correct elliptic curve in the CM method’, Math. Comp. 79 (2010) 545–561.CrossRefGoogle Scholar
Satoh, T., ‘On p-adic point counting algorithms for elliptic curves over finite fields’, Algorithmic Number Theory, 5th International Symposium, ANTS-V Proceedings , Lecture Notes in Computer Science 2369 (Springer, Berlin, 2002) 43–66.Google Scholar
Schönhage, A. and Strassen, V., ‘Schnelle Multiplikation großer Zahlen’, Computing 7 (1971) 281–292.Google Scholar
Schoof, R., ‘Elliptic curves over finite fields and the computation of square roots mod p ’, Math. Comp. 44 (1985) 483–494.Google Scholar
Schoof, R., ‘Counting points on elliptic curves over finite fields’, J. Théor. Nombres Bordeaux 7 (1995) 219–254.Google Scholar
Serre, J.-P., ‘Propriétés galoisiennes des points d’ordre fini des courbes elliptiques’, Invent. Math. 15 (1972) 259–331.Google Scholar
Shparlinski, I. E., ‘On the product of small Elkies primes’, Proc. Amer. Math. Soc. to appear.Google Scholar
Shparlinski, I. E. and Sutherland, A. V., ‘On the distribution of Atkin and Elkies primes’, Found. Comput. Math. 14 (2014) 285–297.Google Scholar
Silverman, J. H., The arithmetic of elliptic curves , 2nd edn (Springer, Dordrecht, 2009).Google Scholar
Sutherland, A. V., ‘Identifying supersingular elliptic curves’, LMS J. Comput. Math. 15 (2012) 317–325.Google Scholar
Sutherland, A. V., ‘On the evaluation of modular polynomials’, ANTS X, Proceedings of the Tenth Algorithmic Number Theory Symposium (Mathematical Sciences Publishers, Berkeley, CA, 2013) 531–555.Google Scholar