Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T16:27:05.961Z Has data issue: false hasContentIssue false
  • English
  • Français

Higher torsion in the Abelianization of the full Bianchi groups

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  01 September 2013

Alexander D. Rahm
Alexander D. Rahm*
Affiliation:
Department of Mathematics, National University of Ireland at Galway,Ireland email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Denote by 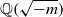$ \mathbb{Q} ( \sqrt{- m} )$, with 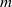$m$ a square-free positive integer, an imaginary quadratic number field, and by 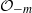${ \mathcal{O} }_{- m} $ its ring of integers. The Bianchi groups are the groups 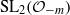${\mathrm{SL} }_{2} ({ \mathcal{O} }_{- m} )$. In the literature, so far there have been no examples of 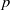$p$-torsion in the integral homology of the full Bianchi groups, for 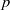$p$ a prime greater than the order of elements of finite order in the Bianchi group, which is at most 6. However, extending the scope of the computations, we can observe examples of torsion in the integral homology of the quotient space, at prime numbers as high as for instance 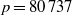$p= 80\hspace{0.167em} 737$ at the discriminant 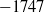$- 1747$.

Supplementary materials are available with this article.

MSC classification

Secondary: 11F75: Cohomology of arithmetic groups
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 16 , October 2013 , pp. 344 - 365
Copyright
© The Author(s) 2013 

References

Aranés, M. T., ‘Modular symbols over number fields’, PhD Thesis, University of Warwick, 2010.Google Scholar
Bianchi, L., ‘Sui gruppi di sostituzioni lineari con coefficienti appartenenti a corpi quadratici immaginarî’, Math. Ann. 40 (1892) no. 3, 332–412.CrossRefGoogle Scholar
Bergeron, N. and Venkatesh, A., ‘The asymptotic growth of torsion homology for arithmetic groups’, J. Inst. Math. Jussieu (2012), to appear, doi: 10.1017/S1474748012000667.CrossRefGoogle Scholar
Brown, K. S., Cohomology of groups, Graduate Texts in Mathematics, 87 (Springer, New York, 1982).CrossRefGoogle Scholar
Bygott, J., ‘Modular forms and modular symbols over imaginary quadratic fields’, PhD Thesis, University of Exeter, 1998.Google Scholar
Cremona, J. E. and Lingham, M. P., ‘Finding all elliptic curves with good reduction outside a given set of primes’, Experiment. Math. 16 (2007) no. 3, 303–312; MR 2367320(2008k:11057).CrossRefGoogle Scholar
Cremona, J. E., ‘Hyperbolic tessellations, modular symbols, and elliptic curves over complex quadratic fields’, Compositio Math. 51 (1984) no. 3, 275–324.Google Scholar
Elstrodt, J., Grunewald, F. and Mennicke, J., Groups acting on hyperbolic space, Springer Monographs in Mathematics (Springer, Berlin, 1998).CrossRefGoogle Scholar
Fine, B., Algebraic theory of the Bianchi groups, Monographs and Textbooks in Pure and Applied Mathematics, 129 (Marcel Dekker Inc., New York, 1989).Google Scholar
Flöge, D., ‘Zur Struktur der ${\mathrm{PSL} }_{2} $ über einigen imaginär-quadratischen Zahlringen’, Dissertation, Johann-Wolfgang-Goethe-Universität, Fachbereich Mathematik, 1980.Google Scholar
Flöge, D., ‘Zur Struktur der ${\mathrm{PSL} }_{2} $ über einigen imaginär-quadratischen Zahlringen’, Math. Z. 183 (1983) no. 2, 255–279.CrossRefGoogle Scholar
Humbert, G., ‘Sur la réduction des formes d’Hermite dans un corps quadratique imaginaire’, C. R. Acad. Sci. Paris 16 (1915) 189–196.Google Scholar
Lingham, M., ‘Modular forms and elliptic curves over imaginary quadratic fields’, PhD Thesis, University of Nottingham, 2005.Google Scholar
Maclachlan, C. and Reid, A. W., The arithmetic of hyperbolic 3-manifolds, Graduate Texts in Mathematics, 219 (Springer-Verlag, New York, 2003).CrossRefGoogle Scholar
Mendoza, E. R., ‘Cohomology of ${\mathrm{PGL} }_{2} $ over imaginary quadratic integers’, Bonner Mathematische Schriften, 128 (Dissertation, Rheinische Friedrich-Wilhelms-Universität, Mathematisches Institut, 1979).Google Scholar
Page, A., ‘Computing arithmetic Kleinian groups’, Preprint, 2012, http://hal.archives-ouvertes.fr/hal-00703043.Google Scholar
Poincaré, H., ‘Mémoire: Les groupes Kleinéens’, Acta Math. 3 (1883) no. 1, 49–92.CrossRefGoogle Scholar
Rahm, A. D., Bianchi.gp, Open source program (GNU general public license), validated by the CNRS: http://www.projet-plume.org/fiche/bianchigp, subject to the Certificat de Compétences en Calcul Intensif (C3I) and part of the GP scripts library of Pari/GP Development Center, 2010.Google Scholar
Rahm, A. D., ‘Homology and $K$ -theory of the Bianchi groups’, C. R. Math. Acad. Sci. Paris 349 (2011) no. 11–12, 615–619; MR 2817377(2012e:20116).CrossRefGoogle Scholar
Rahm, A. D., ‘The homological torsion of ${\mathrm{PSL} }_{2} $ of the imaginary quadratic integers’, Trans. Amer. Math. Soc. 365 (2013) no. 3, 1603–1635; MR 3003276.CrossRefGoogle Scholar
Rahm, A. D., ‘Accessing the Farrell–Tate cohomology of discrete groups’, Preprint, 2012, http://hal.archives-ouvertes.fr/hal-00618167.Google Scholar
Rahm, A. D., ‘On a question of Serre’, C. R. Math. Acad. Sci. Paris 350 (2012) no. 15–16, 741–744; MR 2981344.CrossRefGoogle Scholar
Rahm, A. D. and Fuchs, M., ‘The integral homology of ${\mathrm{PSL} }_{2} $ of imaginary quadratic integers with non-trivial class group’, J. Pure Appl. Algebra 215 (2011) no. 6, 1443–1472; MR 2769243.CrossRefGoogle Scholar
Rahm, A. D. and Şengün, M. H., ‘On level one cuspidal Bianchi modular forms’, LMS J. Comput. Math. 16 (2013) 187–199.CrossRefGoogle Scholar
Riley, R., ‘Applications of a computer implementation of Poincaré’s theorem on fundamental polyhedra’, Math. Comp. 40 (1983) no. 162, 607–632; MR 689477(85b:20064).Google Scholar
Scheutzow, A., ‘Computing rational cohomology and Hecke eigenvalues for Bianchi groups’, J. Number Theory 40 (1992) no. 3, 317–328.CrossRefGoogle Scholar
Schwermer, J. and Vogtmann, K., ‘The integral homology of ${\mathrm{SL} }_{2} $ and ${\mathrm{PSL} }_{2} $ of Euclidean imaginary quadratic integers’, Comment. Math. Helv. 58 (1983) no. 4, 573–598.CrossRefGoogle Scholar
Şengün, M. H., ‘On the integral cohomology of Bianchi groups’, Experiment. Math. 20 (2011) no. 4, 487–505; MR 2859903.CrossRefGoogle Scholar
Şengün, M. H., ‘Arithmetic aspects of Bianchi groups’, Preprint, 2012, arXiv:1204.6697.Google Scholar
Şengün, M. H. and Turkelli, S., ‘Weight reduction for $\mathrm{mod} ~\ell $ Bianchi modular forms’, J. Number Theory 129 (2009) no. 8, 2010–2019; MR 2522720(2010c:11064).CrossRefGoogle Scholar
Serre, J.-P., ‘Le problème des groupes de congruence pour SL(2)’, Ann. of Math. (2) 92 (1970) 489–527.CrossRefGoogle Scholar
Swan, R. G., ‘Generators and relations for certain special linear groups’, Adv. Math. 6 (1971) 1–77.CrossRefGoogle Scholar
Vogtmann, K., ‘Rational homology of Bianchi groups’, Math. Ann. 272 (1985) no. 3, 399–419.CrossRefGoogle Scholar
Whitley, E., ‘Modular symbols and elliptic curves over imaginary quadratic fields’, PhD Thesis, University of Exeter, 1990.Google Scholar
Yasaki, D., ‘Hyperbolic tessellations associated to Bianchi groups’, Proceedings 9th International Symposium on Algorithmic Number Theory (ANTS-IX), Nancy, France, 19–23 July 2010, 385–396. MR 2721434(2012g:11069).CrossRefGoogle Scholar
Supplementary material: File

Rahm Supplementary Material

Supplementary Material

Download Rahm Supplementary Material(File)
File 60.7 KB