Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T23:10:04.291Z Has data issue: false hasContentIssue false
  • English
  • Français

Databases of elliptic curves ordered by height and distributions of Selmer groups and ranks

Part of: Number theory Arithmetic algebraic geometry

Published online by Cambridge University Press:  26 August 2016

Jennifer S. Balakrishnan ,
Wei Ho ,
Nathan Kaplan ,
Simon Spicer ,
William Stein  and
James Weigandt
Jennifer S. Balakrishnan
Affiliation:
Mathematical Institute, University of Oxford, Woodstock Road, Oxford OX2 6GG, United Kingdom email [email protected]
Wei Ho
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, MI 48109, USA email [email protected]
Nathan Kaplan
Affiliation:
Department of Mathematics, University of California, Irvine, Irvine, CA 92697, USA email [email protected]
Simon Spicer
Affiliation:
Facebook Inc., 1 Hacker Way, Menlo Park, CA 94025, USA email [email protected]
William Stein
Affiliation:
Department of Mathematics, University of Washington, Seattle, WA 98195-4350, USA email [email protected]
James Weigandt
Affiliation:
Institute for Computational and Experimental Research in Mathematics, Brown University, Providence, RI 02912, USA email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Most systematic tables of data associated to ranks of elliptic curves order the curves by conductor. Recent developments, led by work of Bhargava and Shankar studying the average sizes of $n$-Selmer groups, have given new upper bounds on the average algebraic rank in families of elliptic curves over 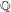$\mathbb{Q}$, ordered by height. We describe databases of elliptic curves over 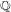$\mathbb{Q}$, ordered by height, in which we compute ranks and $2$-Selmer group sizes, the distributions of which may also be compared to these theoretical results. A striking new phenomenon that we observe in our database is that the average rank eventually decreases as height increases.

MSC classification

Primary: 11G05: Elliptic curves over global fields
Secondary: 11-04: Explicit machine computation and programs (not the theory of computation or programming)
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 19 , Special Issue A: Algorithmic Number Theory Symposium XII , 2016 , pp. 351 - 370
Copyright
© The Author(s) 2016 

References

Balakrishnan, J. S., Ho, W., Kaplan, N., Spicer, S., Stein, W. and Weigandt, J., http://wstein.org/papers/2016-height/.Google Scholar
Bektemirov, B., Mazur, B., Stein, W. and Watkins, M., ‘Average ranks of elliptic curves: tension between data and conjecture’, Bull. Amer. Math. Soc. (N.S.) 44 (2007) no. 2, 233–254.Google Scholar
Bennett, M. and Rechnitzer, A., ‘Computing elliptic curves over $\mathbb{Q}$ : bad reduction at one prime’, Preprint.Google Scholar
Bhargava, M. and Ho, W., ‘On the average sizes of Selmer groups in families of elliptic curves’, Preprint.Google Scholar
Bhargava, M., Kane, D. M., Lenstra, H. W. Jr., Poonen, B. and Rains, E., ‘Modeling the distribution of ranks, Selmer groups, and Shafarevich-Tate groups of elliptic curves’, Camb. J. Math. 3 (2015) no. 3, 275–321.Google Scholar
Bhargava, M. and Shankar, A., ‘Binary quartic forms having bounded invariants, and the boundedness of the average rank of elliptic curves’, Ann. of Math. (2) 181 (2015) no. 1, 191–242.Google Scholar
Bhargava, M. and Shankar, A., ‘Ternary cubic forms having bounded invariants, and the existence of a positive proportion of elliptic curves having rank 0’, Ann. of Math. (2) 181 (2015) no. 2, 587–621.Google Scholar
Bhargava, M. and Shankar, A., ‘The average number of elements in the $4$ -Selmer groups of elliptic curves is $7$ ’, Preprint, 2013, arXiv:1312.7333.Google Scholar
Bhargava, M. and Shankar, A., ‘The average size of the $5$ -Selmer group of elliptic curves is $6$ , and the average rank is less than $1$ ’, Preprint, 2013, arXiv:1312.7859.Google Scholar
Birch, B. J. and Kuyk, W. (eds), Modular functions of one variable, Vol. IV , Lecture Notes in Mathematics 476 (Springer, Berlin–New York, 1975).Google Scholar
Bober, J. W., ‘Conditionally bounding analytic ranks of elliptic curves’, ANTS X—Proceedings of the Tenth Algorithmic Number Theory Symposium , Open Book Series 1 (Mathematical Sciences Publishers, Berkeley, CA, 2013) 135–144.Google Scholar
Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system. I. The user language’, J. Symbolic Comput. 24 (1997) no. 3–4, 235–265, Computational algebra and number theory (London, 1993).Google Scholar
Brumer, A., ‘The average rank of elliptic curves. I’, Invent. Math. 109 (1992) no. 3, 445–472.Google Scholar
Brumer, A. and McGuinness, O., ‘The behavior of the Mordell-Weil group of elliptic curves’, Bull. Amer. Math. Soc. (N.S.) 23 (1990) no. 2, 375–382.Google Scholar
Cremona, J., Algorithms for modular elliptic curves , 2nd edn (Cambridge University Press, Cambridge, 1997).Google Scholar
Cremona, J., ecdata: 2016-02-07, http://dx.doi.org/10.5281/zenodo.45657, February 2016.Google Scholar
Delaunay, C., ‘Heuristics on Tate-Shafarevitch groups of elliptic curves defined over ℚ’, Experiment. Math. 10 (2001) no. 2, 191–196.Google Scholar
Delaunay, C. and Jouhet, F., ‘ p ℓ -torsion points in finite abelian groups and combinatorial identities’, Adv. Math. 258 (2014) 13–45.Google Scholar
Goldfeld, D., ‘Conjectures on elliptic curves over quadratic fields’, Number theory, Carbondale , Proceedings of Southern Illinois Conference, Southern Illinois University, Carbondale, Ill, 1979, Lecture Notes in Mathematics 751 (Springer, Berlin, 1979) 108–118.Google Scholar
Harron, R. and Snowden, A., ‘Counting elliptic curves with prescribed torsion’, J. reine angew. Math., to appear, doi:10.1515/crelle-2014-0107.Google Scholar
Heath-Brown, D. R., ‘The average analytic rank of elliptic curves’, Duke Math. J. 122 (2004) no. 3, 591–623, 04.Google Scholar
Iwaniec, H. and Kowalski, E., Analytic number theory , American Mathematical Society Colloquium Publications 53 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Katz, N. M. and Sarnak, P., Random matrices, Frobenius eigenvalues, and monodromy , American Mathematical Society Colloquium Publications 45 (American Mathematical Society, Providence, RI, 1999).Google Scholar
Mestre, J.-F., ‘Formules explicites et minorations de conducteurs de variétés algébriques’, Compositio Math. 58 (1986) no. 2, 209–232.Google Scholar
Park, J., Poonen, B., Voight, J. and Wood, M., ‘Heuristics for boundedness of ranks of elliptic curves over $\mathbb{Q}$ ’, Preprint, 2016, arXiv:1602.01431.Google Scholar
Poonen, B. and Rains, E., ‘Random maximal isotropic subspaces and Selmer groups’, J. Amer. Math. Soc. 25 (2012) no. 1, 245–269.Google Scholar
SageMath, Inc. SageMathCloud, 2016. https://cloud.sagemath.com.Google Scholar
Spicer, S. V., The zeros of elliptic curve $L$ -functions: analytic algorithms with explicit time complexity, PhD Thesis, University of Washington, 2015.Google Scholar
Stein, W. A. and Watkins, M., ‘A database of elliptic curves—first report’, Algorithmic number theory (Sydney, 2002) , Lecture Notes in Computer Science 2369 (Springer, Berlin, 2002) 267–275.Google Scholar
The SageMath Developers. Sage Mathematics Software (Version 6.9), 2015. http://www.sagemath.org.Google Scholar
Watkins, M., ‘Some heuristics about elliptic curves’, Experiment. Math. 17 (2008) no. 1, 105–125.Google Scholar
Young, M., ‘Low-lying zeros of families of elliptic curves’, J. Amer. Math. Soc. 19 (2006) no. 1, 205–250.Google Scholar