Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-23T06:53:24.713Z Has data issue: false hasContentIssue false
  • English
  • Français

Computing characters of groups with central subgroups

Part of: Representation theory of groups

Published online by Cambridge University Press:  07 November 2013

Vahid Dabbaghian  and
John D. Dixon
Vahid Dabbaghian
Affiliation:
MoCSSy Program The IRMACS Centre Simon Fraser University Burnaby, BC V5A 1S6 Canada email [email protected]
John D. Dixon
Affiliation:
School of Mathematics and Statistics Carleton University Ottawa, ON K1S 5B6 Canada email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The so-called Burnside–Dixon–Schneider (BDS) method, currently used as the default method of computing character tables in GAP for groups which are not solvable, is often inefficient in dealing with groups with large centres. If 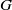$G$ is a finite group with centre 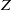$Z$ and 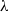$\lambda $ a linear character of 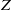$Z$, then we describe a method of computing the set 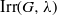$\mathrm{Irr} (G, \lambda )$ of irreducible characters 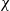$\chi $ of 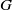$G$ whose restriction 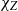${\chi }_{Z} $ is a multiple of 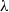$\lambda $. This modification of the BDS method involves only 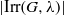$\vert \mathrm{Irr} (G, \lambda )\vert $ conjugacy classes of 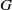$G$ and so is relatively fast. A generalization of the method can be applied to computation of small sets of characters of groups with a solvable normal subgroup.

Supplementary materials are available with this article.

MSC classification

Secondary: 20C15: Ordinary representations and characters 20C40: Computational methods
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 16 , October 2013 , pp. 398 - 406
Copyright
© The Author(s) 2013 

References

Bosma, W., Cannon, J. and Playoust, C., ‘The Magma algebra system I: the user language’, J. Symbolic Comput. 24 (1997) 235–265.CrossRefGoogle Scholar
Breuer, T., ‘Computing character tables of groups of type M.G.A ’, LMS J. Comput. Math. 14 (2011) 173–178.CrossRefGoogle Scholar
Dixon, J. D., ‘High speed computation of group characters’, Numer. Math. 10 (1967) 446–450.CrossRefGoogle Scholar
Fischer, B., ‘Clifford-matrices’, Representation theory of finite groups and finite-dimensional algebras, Bielefeld, 1991 (Birkhäuser, Basel, 1991) 1–16.Google Scholar
The GAP Group, GAP—Groups, Algorithms, and Programming, version 4.5.5, 2012, http://www.gap-system.org.Google Scholar
Holt, D. F. and Plesken, W., Perfect groups (Clarendon Press, Oxford, 1989).Google Scholar
Hulpke, J. A., Zur Berechnung von Charaktertafeln, Diplomarbeit im Fach Mathematik an der Rheinisch-Westfälischen Technischen Hochschule, Aachen, 1993.Google Scholar
Isaacs, I. M., Character theory of finite groups (Academic Press, New York, 1976).Google Scholar
Lux, K. and Pahlings, H., Representations of groups: a computational approach (Cambridge University Press, Cambridge, 2010).CrossRefGoogle Scholar
Pahlings, H., ‘The character table of ${ 2}_{+ }^{1+ 22} . C{o}_{2} $ ’, J. Algebra 315 (2007) 301–323.CrossRefGoogle Scholar
Schneider, G. J. A., ‘Dixon’s character table algorithm revisited’, J. Symbolic Comput. 9 (1990) 601–606.CrossRefGoogle Scholar
Unger, W. R., ‘Computing the character table of a finite group’, J. Symbolic Comput. 41 (2006) 847–862.CrossRefGoogle Scholar
Supplementary material: File

Dabbaghian and Dixon Supplementary Material

Data

Download Dabbaghian and Dixon Supplementary Material(File)
File 42 KB