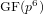Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T03:08:29.403Z Has data issue: false hasContentIssue false
  • English
  • Français

Collecting relations for the number field sieve in $\text{GF}(p^{6})$

Part of: Finite fields and commutative rings (number-theoretic aspects) Number theory Computational number theory

Published online by Cambridge University Press:  26 August 2016

Pierrick Gaudry ,
Laurent Grémy  and
Marion Videau
Pierrick Gaudry
Affiliation:
INRIA, CNRS, Université de Lorraine, Nancy, France email [email protected]
Laurent Grémy
Affiliation:
INRIA, CNRS, Université de Lorraine, Nancy, France email [email protected]
Marion Videau
Affiliation:
Quarkslab, Paris, France INRIA, CNRS, Université de Lorraine, Nancy, France email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In order to assess the security of cryptosystems based on the discrete logarithm problem in non-prime finite fields, as are the torus-based or pairing-based ones, we investigate thoroughly the case in 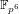$\mathbb{F}_{p^{6}}$ with the number field sieve. We provide new insights, improvements, and comparisons between different methods to select polynomials intended for a sieve in dimension 3 using a special-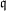$\mathfrak{q}$ strategy. We also take into account the Galois action to increase the relation productivity of the sieving phase. To validate our results, we ran several experiments and real computations for various polynomial selection methods and field sizes with our publicly available implementation of the sieve in dimension 3, with special-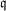$\mathfrak{q}$ and various enumeration strategies.

MSC classification

Primary: 11T71: Algebraic coding theory; cryptography 11Y40: Algebraic number theory computations 11-04: Explicit machine computation and programs (not the theory of computation or programming)
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 19 , Special Issue A: Algorithmic Number Theory Symposium XII , 2016 , pp. 332 - 350
Copyright
© The Author(s) 2016 

References

Bai, S., Brent, R. and Thomé, E., ‘Root optimization of polynomials in the number field sieve’, Math. Comp. 84 (2015) 2447–2457.CrossRefGoogle Scholar
Barbulescu, R., Gaudry, P., Guillevic, A. and Morain, F., ‘Improving NFS for the discrete logarithm problem in non-prime finite fields’, EUROCRYPT 2015 , Lecture Notes in Computer Science 9056 (eds Oswald, E. and Fischlin, M.; Springer, 2015) 129–155.CrossRefGoogle Scholar
Barbulescu, R., Gaudry, P., Joux, A. and Thomé, E., ‘A heuristic quasi-polynomial algorithm for discrete logarithm in finite fields of small characteristic’, EUROCRYPT 2014 , Lecture Notes in Computer Science 8441 (eds Nguyen, P. and Oswald, E.; Springer, Berlin, Heidelberg, 2014) 1–16.Google Scholar
Barbulescu, R., Gaudry, P. and Kleinjung, T., ‘The tower number field sieve’, ASIACRYPT 2015 , Lecture Notes in Computer Science 9453 (eds Iwata, T. and Cheon, J. H.; Springer, Berlin, Heidelberg, 2015) 31–55.CrossRefGoogle Scholar
Barbulescu, R. and Lachand, A., ‘Some mathematical remarks on the polynomial selection in NFS’, Math. Comp., published online (2016), doi:10.1090/mcom/3112.CrossRefGoogle Scholar
Barbulescu, R. and Pierrot, C., ‘The multiple number field sieve for medium and high characteristic finite fields’, LMS J. Comput. Math. 17 (2014) 230–246.CrossRefGoogle Scholar
Cohen, H., A course in algorithmic algebraic number theory , Graduate Texts in Mathematics 138 (Springer, Berlin, Heidelberg, 1993).Google Scholar
Commeine, A. and Semaev, I., ‘An algorithm to solve the discrete logarithm problem with the number field sieve’, PKC 2006 , Lecture Notes in Computer Science 3958 (eds Yung, M., Dodis, Y., Kiayias, A. and Malkin, T.; Springer, Berlin, Heidelberg, 2006) 174–190.Google Scholar
Coppersmith, D., ‘Modifications to the number field sieve’, J. Cryptology 6 (1993) no. 3, 169–180.CrossRefGoogle Scholar
Franke, J. and Kleinjung, T., ‘Continued fractions and lattice sieving’, SHARCS’05 – Special-purpose Hardware for Attacking Cryptographic Systems (2005), http://www.sharcs.org/.Google Scholar
Freeman, D., Scott, M. and Teske, E., ‘A taxonomy of pairing-friendly elliptic curves’, J. Cryptology 23 (2010) 224–280.CrossRefGoogle Scholar
González, Á., ‘Measurement of areas on a sphere using Fibonacci and latitude–longitude lattices’, Math. Geosci. (2010) 42–49.Google Scholar
Gordon, D. M., ‘Discrete logarithms in GF(p) using the number field sieve’, SIAM J. Discrete Math. 6 (1993) no. 1, 124–138.CrossRefGoogle Scholar
Guillevic, A., ‘Computing individual discrete logarithms faster in GF(p n ) with the NFS-DL algorithm’, ASIACRYPT 2015 , Lecture Notes in Computer Science 9452 (eds Iwata, T. and Cheon, J. H.; Springer, Berlin, Heidelberg, 2015) 149–173.CrossRefGoogle Scholar
Hanrot, G., Pujol, X. and Stehlé, D., ‘Algorithms for the shortest and closest lattice vector problems’, Coding and Cryptology — Third International Workshop, IWCC 2011 , Lecture Notes in Computer Science 6639 (eds Chee, Y. M., Guo, Z., Ling, S., Shao, F., Tang, Y., Wang, H. and Xing, C.; Springer, Berlin, Heidelberg, 2011) 159–190.Google Scholar
Hayasaka, K., Aoki, K., Kobayashi, T. and Takagi, T., ‘An experiment of number field sieve for discrete logarithm problem over GF(p 12 )’, Number theory and cryptography , Lecture Notes in Computer Science 8260 (eds Fischlin, M. and Katzenbeisser, S.; Springer, Berlin, Heidelberg, 2013) 108–120.Google Scholar
Hayasaka, K., Aoki, K., Kobayashi, T. and Takagi, T., ‘A construction of 3-dimensional lattice sieve for number field sieve over $\mathbb{F}_{p^{n}}$ ’, Cryptology ePrint Archive, 2015/1179, 2015.Google Scholar
Joux, A. and Lercier, R., ‘Improvements to the general number field sieve for discrete logarithms in prime fields’, Math. Comp. 72 (2003) no. 242, 953–967.CrossRefGoogle Scholar
Joux, A., Lercier, R., Smart, N. P. and Vercauteren, F., ‘The number field sieve in the medium prime case’, CRYPTO 2006 , Lecture Notes in Computer Science 4117 (ed. Dwork, C.; Springer, Berlin, Heidelberg, 2006) 326–344.CrossRefGoogle Scholar
Joux, A. and Pierrot, C., ‘The special number field sieve in F p n — application to pairing-friendly constructions’, Pairing 2013 , Lecture Notes in Computer Science 8365 (eds Cao, Z. and Zhang, F.; Springer, Cham, 2013) 45–61.Google Scholar
Kim, T. and Barbulescu, R., ‘Extended tower number field sieve: a new complexity for medium prime case’, CRYPTO 2016, Lecture Notes in Computer Science (Springer), to appear; Cryptology ePrint Archive, 2015/1027, 2015.CrossRefGoogle Scholar
Kleinjung, T., ‘On polynomial selection for the general number field sieve’, Math. Comp. 75 (2006) 2037–2047.CrossRefGoogle Scholar
Lenstra, A. K. and Verheul, E. R., ‘The XTR public key system’, CRYPTO 2000 , Lecture Notes in Computer Science 1880 (ed. Bellare, M.; Springer, 2000) 1–19.Google Scholar
Murphy, B. A., ‘Polynomial selection for the number field sieve integer factorisation algorithm’, PhD Thesis, Australian National University, 1999.Google Scholar
Pierrot, C., ‘The multiple number field sieve with conjugation and generalized Joux–Lercier methods’, EUROCRYPT 2015 , Lecture Notes in Computer Science 9056 (eds Oswald, E. and Fischlin, M.; Springer, Berlin, Heidelberg, 2015) 156–170.CrossRefGoogle Scholar
Pollard, J., ‘The lattice sieve’, The development of the number field sieve , Lecture Notes in Mathematics 1554 (eds Lenstra, A. K. and Lenstra, H. W. Jr.; Springer, Berlin, Heidelberg, 1993) 43–49.CrossRefGoogle Scholar
Rubin, K. and Silverberg, A., ‘Torus-based cryptography’, CRYPTO 2003 , Lecture Notes in Computer Science 2729 (ed. Boneh, D.; Springer, Berlin, Heidelberg, 2003) 349–365.CrossRefGoogle Scholar
Sarkar, P. and Singh, S., ‘New complexity trade-offs for the (multiple) number field sieve algorithm in non-prime fields’, EUROCRYPT 2016 , Lecture Notes in Computer Science 9665 (eds Fischlin, M. and Coron, J. S.; Springer, Berlin, Heidelberg, 2016) 429–458.CrossRefGoogle Scholar
Schirokauer, O., ‘Virtual logarithms’, J. Algorithms 57 (2005) 140–147.CrossRefGoogle Scholar
Schirokauer, O., ‘Discrete logarithms and local units’, Philos. Trans. A 345 (1993) no. 1676, 409–423.Google Scholar
The CADO-NFS Development Team: CADO-NFS, an implementation of the number field sieve algorithm, 2015, http://cado-nfs.gforge.inria.fr/, release 2.2.0.Google Scholar
Zajac, P., ‘Discrete logarithm problem in degree six finite fields’, PhD Thesis, Slovak University of Technology, 2008, http://www.kaivt.elf.stuba.sk/kaivt/Vyskum/XTRDL.Google Scholar
Zajac, P., ‘On the use of the lattice sieve in the 3D NFS’, Tatra Mt. Math. Publ. 45 (2010) 161–172.Google Scholar