Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-24T16:32:00.610Z Has data issue: false hasContentIssue false
  • English
  • Français

Certain aspects of holomorphic function theory on some genus-zero arithmetic groups

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  01 March 2017

Jay Jorgenson ,
Lejla Smajlović  and
Holger Then
Jay Jorgenson
Affiliation:
Department of Mathematics, The City College of New York, Convent Avenue at 138th Street, New York, NY 10031, USA email [email protected]
Lejla Smajlović
Affiliation:
Department of Mathematics, University of Sarajevo, Zmaja od Bosne 35, 71 000 Sarajevo, Bosnia and Herzegovina email [email protected]
Holger Then
Affiliation:
Department of Mathematics, University of Bristol, University Walk, Bristol, BS8 1TW, United Kingdom email [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

There are a number of fundamental results in the study of holomorphic function theory associated to the discrete group 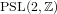$\operatorname{PSL}(2,\mathbb{Z})$, including the following statements: the ring of holomorphic modular forms is generated by the holomorphic Eisenstein series of weights four and six, denoted by 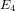$E_{4}$ and 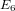$E_{6}$; the smallest-weight cusp form $\unicode[STIX]{x1D6E5}$ has weight twelve and can be written as a polynomial in 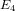$E_{4}$ and 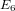$E_{6}$; and the Hauptmodul 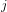$j$ can be written as a multiple of 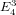$E_{4}^{3}$ divided by 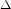$\unicode[STIX]{x1D6E5}$. The goal of the present article is to seek generalizations of these results to some other genus-zero arithmetic groups 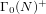$\unicode[STIX]{x1D6E4}_{0}(N)^{+}$ with square-free level 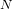$N$, which are related to ‘Monstrous moonshine conjectures’. Certain aspects of our results are generated from extensive computer analysis; as a result, many of the space-consuming results are made available on a publicly accessible web site. However, we do present in this article specific results for certain low-level groups.

MSC classification

Primary: 11F12: Automorphic forms, one variable
Secondary: 11F20: Dedekind eta function, Dedekind sums
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 19 , Issue 2 , 2016 , pp. 360 - 381
Copyright
© The Author(s) 2017 

References

Borel, A., Chowla, S., Herz, C. S., Iwasawa, K. and Serre, J. P. (eds), Seminar on complex multiplication , Lecture Notes in Mathematics 21 (Springer, Berlin–New York, 1966).CrossRefGoogle Scholar
Conway, J. H. and Norton, S. P., ‘Monstrous moonshine’, Bull. Lond. Math. Soc. 11 (1979) 308–339.Google Scholar
Cummins, C. J., ‘Congruence subgroups of groups commensurable with PSL(2, ℤ) of genus 0 and 1’, Exp. Math. 13 (2004) 361–382.Google Scholar
Gannon, T., ‘Monstrous moonshine: the first twenty-five years’, Bull. Lond. Math. Soc. 38 (2006) 1–33.CrossRefGoogle Scholar
Gannon, T., Moonshine beyond the monster. The bridge connecting algebra, modular forms and physics , Cambridge Monographs on Mathematical Physics (Cambridge University Press, Cambridge, 2006).CrossRefGoogle Scholar
Jorgenson, J., Smajlović, L. and Then, H., ‘On the distribution of eigenvalues of Maass forms on certain moonshine groups’, Math. Comp. 83 (2014) 3039–3070.Google Scholar
Jorgenson, J., Smajlović, L. and Then, H., ‘Kronecker’s limit formula, holomorphic modular functions and q-expansions on certain arithmetic groups’, Exp. Math. 25 (2016) 295–320.Google Scholar
Jorgenson, J., Smajlović, L. and Then, H., Data page, http://www.efsa.unsa.ba/∼lejla.smajlovic/.Google Scholar
Miezaki, T., Nozaki, H. and Shigezumi, J., ‘On the zeros of Eisenstein series for 𝛤0 ∗(2) and 𝛤0 ∗(3)’, J. Math. Soc. Japan 59 (2007) 693–706.Google Scholar
Serre, J.-P., A course in arithmetic , Graduate Texts in Mathematics 7 (Springer, New York, 1973).CrossRefGoogle Scholar