Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T05:28:33.424Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability and dynamics of a cosh-Gaussian laser beam in relativistic thermal quantum plasma

Published online by Cambridge University Press:  01 October 2018

Ranju Mahajan ,
Richa ,
Tarsem Singh Gill ,
Ravinder Kaur  and
Munish Aggarwal
Ranju Mahajan*
Affiliation:
Department of Physics, Lyallpur Khalsa College, Jalandhar 144001, India
Richa
Affiliation:
Research Scholar, I.K. Gujral Punjab Technical University, Kapurthala 144603, India
Tarsem Singh Gill*
Affiliation:
Department of Physics, Guru Nanak Dev University, Amritsar 143005, India
Ravinder Kaur
Affiliation:
Department of Physics, DAV College, Jalandhar 144001, India
Munish Aggarwal
Affiliation:
Department of Applied Science, Lyallpur Khalsa College of Engineering, Jalandhar 144001, India
*
Author for correspondence: Ranju Mahajan and Tarsem Singh Gill, Department of Physics, Lyallpur Khalsa College, Jalandhar 144001, India; Department of Physics, Guru Nanak Dev University, Amritsar 143005, India E-mail: [email protected], [email protected]
Author for correspondence: Ranju Mahajan and Tarsem Singh Gill, Department of Physics, Lyallpur Khalsa College, Jalandhar 144001, India; Department of Physics, Guru Nanak Dev University, Amritsar 143005, India E-mail: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper presents an investigation on the self-focusing of a cosh-Gaussian laser beam in the thermal quantum plasma (TQP) by taking into account the effects of relativistic nonlinearity. An appropriate nonlinear Schrödinger equation has been solved analytically by applying the variational approach. The self-focusing and the self-phase modulation are examined under a variety of parameters. The self-trapping of a cosh-Gaussian laser beam is further studied at various values of the decentered parameter, b with different absorption levels, 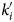${k}^{\prime}_i$. Numerical analysis shows that these parameters play a vital role in propagation characteristics. The significant contribution of the quantum effects to enhance the self-focusing and minimize the longitudinal phase has been observed. Further, a comparison has been made with the classical relativistic (CR), the relativistic cold quantum (RCQ), and the thermal quantum (TQ) regimes. The self-focusing is found to occur earlier and is strongest for the case of TQP in the present analysis.

Keywords

Cosh-Gaussian beamself-focusing and self-trappingself-phase modulationrelativistic thermal quantum plasma
Type
Research Article
Information
Laser and Particle Beams , Volume 36 , Issue 3 , September 2018 , pp. 341 - 352
Copyright
Copyright © Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akhmanov, SA, Sukhorukov, AP and Khokhlov, RV (1968) Self-focusing and diffraction of light in a nonlinear medium. Soviet Physics Uspekhi 10, 609–636.Google Scholar
Ali, S and Shukla, PK (2006) Potential distributions around a moving test charge in quantum plasmas. Physics of Plasmas 13, 102112(1–7).Google Scholar
Anderson, D (1978) Stationary self-trapped laser beams in plasma. Physica Scripta 18, 35–36.Google Scholar
Anderson, D and Bonnedal, M (1979) Variational approach to nonlinear self-focusing of Gaussian laser beams. Physics of Fluids 22, 105–119.Google Scholar
Andreev, AV (2000) Self-consistent equations for the interaction of an atom with an electromagnetic field of arbitrary intensity. JETP Letters 72, 238–240.Google Scholar
Askar'yan, GA (1962) Effect of the gradient of a strong electromagnetic beam on electron and atoms. Journal of Experimental and Theoretical Physics 42, 1567–1570.Google Scholar
Azechi, H and FIREX Project (2006) Present status of the FIREX programme for the demonstration of ignition and burn. Plasma Physics and Controlled Fusion 48, 267.Google Scholar
Azechi, H, Jitsuno, T, Kanabe, T, Katayama, M, Mima, K, Miyanaga, N, Nakai, M, Nakai, S, Nakaishi, H, Nakatsuka, M, Nishiguchi, A, Norrays, PA, Setsuhara, Y, Takagi, M, Yamanaka, M and Yamanaka, C (1991) High-density compression experiments at ILE, Osaka. Laser and Particle. Beams 9, 193–207.Google Scholar
Baykal, Y (2004) Correlation and structure functions of Hermite-sinusoidal-Gaussian laser beams in a turbulent atmosphere. Journal of the Optical Society of America A: Optics and Image Science 21, 1290–1299.Google Scholar
Belafhal, A and Ibnchaikh, M (2000) Comment on propagation properties of Hermite-cosh-Gaussian laser beams. Optics Communications 186, 269.Google Scholar
Bokaei, B and Niknam, AR (2014) Increasing the upper-limit intensity and temperature range for thermal self-focusing of a laser beam by using plasma density ramp-up. Physics of Plasmas 21, 032309.Google Scholar
Chabrier, G, Douchin, F and Potekhin, AY (2002) Dense astrophysical plasmas. Condensed Matter: An Institute of Physics Journal 14, 9133.Google Scholar
Chiao, RY, Garmire, E and Townes, CH (1964) Self-trapping of optical beams. Physical Review Letters 13, 479–482.Google Scholar
Eliasson, B and Shukla, PK (2012) Relativistic x-ray quantum free-electron lasers: a collective KleinGordon model. Plasma Physics and Controlled Fusion 54, 124011.Google Scholar
Esarey, E, Sprangle, P, Krall, J and Ting, A (1997) Self-focusing and guiding of short laser pulses in ionizing gases and plasmas. IEEE Journal of Quantum Electronics 33, 1879–1914.Google Scholar
Faenov, A Ya, Colgan, J, Hansen, SB, Zhidkov, A, Pikuz, TA, Nishiuchi, M, Pikuz, SA, Skobelev, I Yu, Abdallah, J, Sakaki, H, Sagisaka, A, Pirozhkov, AS, Ogura, K, Fukuda, Y, Kanasaki, M, Hasegawa, N, Nishikino, M, Kando, M, Watanabe, Y, Kawachi, T, Masuda, S, Hosokai, T, Kodama, R and Kondo, K (2015) Nonlinear increase of X-ray intensities from thin foils irradiated with a 200 TW femtosecond laser. Scientific Reports 5, 13436.Google Scholar
Firth, WJ (1977) Propagation of laser beams through inhomogeneous media. Optics Communications 22, 226–230.Google Scholar
Gill, TS, Kaur, R and Mahajan, R (2010a) Propagation of high power electromagnetic beam in relativistic magnetoplasma: Higher order paraxial ray theory. Physics of Plasmas 17, 093101.Google Scholar
Gill, TS, Mahajan, R and Kaur, R (2010b) Relativistic and ponderomotive effects on evolution of laser beam in a non-uniform plasma channel. Laser and Particle Beams 28, 11–20.Google Scholar
Gill, TS, Mahajan, R and Kaur, R (2010c) Relativistic and ponderomotive effects on evolution of dark hollow Gaussian electromagnetic beams in a plasma. Laser and Particle Beams 28, 521–529.Google Scholar
Gill, TS, Mahajan, R and Kaur, R (2011) Self-focusing of cosh-Gaussian laser beam in a plasma with weakly relativistic and ponderomotive regime. Physics of Plasmas 18, 033110.Google Scholar
Glenzer, SH and Redmer, R (2009) X-ray Thomson scattering in high energy density plasmas. Reviews of Modern Physics 81, 1625.Google Scholar
Glenzer, SH, Landen, OL, Neumayer, P, Lee, RW, Widmann, K, Pollaine, SW, Wallace, RJ, Gregori, G, Höll, A, Bornath, T, Thiele, R, Schwarz, V, Kraeft, W-D and Redmer, R (2007) Observations of plasmons in warm dense matter. Physical Review Letters 98, 065002.Google Scholar
Gondarenko, NA, Ossakow, SL and Milikh, GM (2005) Generation and evolution of density irregularities due to self-focusing in ionospheric modifications. Journal of Geophysical Research 110, A093041–13.Google Scholar
Gupta, DN and Suk, H (2007) Electron acceleration to high energy by using two chirped lasers. Laser and Particle Beams 25, 31.Google Scholar
Guzdar, PN, Chaturvedi, PK, Papadopoulos, K and Ossakow, SL (1998) The thermal self-focusing instability near the critical surface in the high-latitude ionosphere. Journal of Geophysical Research 103, 2231.Google Scholar
Haas, FB (2011) An introduction to quantum plasmas. Brazilian Journal of Physics 41, 349–363.Google Scholar
Habibi, M and Ghamari, F (2012a) Stationary self-focusing of intense laser beam in cold quantum plasma using ramp density profile. Physics of Plasmas 19, 103110.Google Scholar
Habibi, M and Ghamari, F (2012b) Investigation of non-stationary self-focusing of intense laser pulse in cold quantum plasma using ramp density profile. Physics of Plasmas 19, 113109.Google Scholar
Habibi, M and Ghamari, F (2014) Relativistic self-focusing of ultra-high intensity x-ray laser beams in warm quantum plasma with upward density profile. Physics of Plasmas 21, 052705.Google Scholar
Habibi, M and Ghamari, F (2015a) Improved focusing of a cosh-Gaussian laser beam in quantum plasma: higher order paraxial theory. IEEE Transactions on Plasma Science 43, 2160–2165.Google Scholar
Habibi, M and Ghamari, F (2015b) Significant enhancement in self-focusing of high-power laser beam through dense plasmas by ramp density profile. Journal of Optical Society of America B 32, 1429.Google Scholar
Hefferon, G, Sharma, A and Kourakis, I (2010) Electromagnetic pulse compression and energy localization in quantum plasmas. Physics Letters A 208, 012087.Google Scholar
Hora, H (2007) New aspects for fusion energy using inertial confinement. Laser and Particle Beams 25, 37–45.Google Scholar
Honda, M, Meyer-Ter-Vehn, J and Pukhov, A (2000) Two-dimensional particle-in-cell simulation for magnetized transport of ultra-high relativistic currents in plasma. Physics of Plasmas 7, 1302.Google Scholar
Jung, YD and Murakami, I (2009) Quantum effects on magnetization due to ponderomotive force in cold quantum plasmas. Physics Letters A 373, 969–971.Google Scholar
Karlsson, M, Anderson, D and Desaix, M (1992) Dynamics of self-focusing and self-phase modulation in a parabolic index optical fiber. Optics Letters 17, 22.Google Scholar
Karlsson, M, Anderson, D, Desaix, M and Lisak, M (1991) Dynamic effects of Kerr nonlinearity and spatial diffraction on self-phase modulation of optical pulses. Optics Letters 16, 1373.Google Scholar
Kaur, R, Gill, TS and Mahajan, R (2010) Self-focusing, self modulation and stability properties of laser beam propagating in plasma: A variational approach. Journal of Physics: Conference Series, 969–971.Google Scholar
Kaur, R, Gill, TS and Mahajan, R (2011) Steady state self-focusing, self-phase modulation of laser beam in an inhomogeneous plasma. Optik 122, 375–380.Google Scholar
Kelley, PL (1965) Self-focusing of laser beams and stimulated Raman gain in liquids. Physical Review Letters 15, 1010–1012.Google Scholar
Kodama, R, Norreys, PA, Mima, K, Dangor, AE, Evans, RG, Fujita, H, Kitagawa, Y, Krushelnick, K, Miyakoshi, T, Miyanaga, N, Norimatsu, T, Rose, SJ, Shozaki, T, Shigemori, K, Sunahara, A, Tampo, M, Tanaka, KA, Toyama, Y, Yamanaka, T and Zepf, M (2001) Fast heating of ultrahigh-density plasma as a step towards laser fusion ignition. Nature 412, 798–802.Google Scholar
Kremp, D, Bornath, T, Bonitz, M and Schlanges, M (1999) Quantum kinetic theory of plasmas in strong laser fields. Physical Review E 60, 4725.Google Scholar
Lam, JF, Lippmann, B and Tappert, F (1977) Self-trapped laser beams in plasma. Physics of Fluids 20, 1176.Google Scholar
Lakshman, M and Rajasekar, S (2003) Nonlinear Dynamics. Springer Verlag.Google Scholar
Landen, OL, Farley, DR, Glendinning, SG, Logory, LM, Bell, PM, Koch, JA, Lee, FD, Bradley, DK, Kalantar, DH, Back, CA and Tarner, RE (2001) X-ray backlighting for the National Ignition Facility. Review of Scientific Instruments 72, 627.Google Scholar
Lee, RW, Moon, SJ, Chung, HK, Rozmus, W, Baldis, HA, Gregori, G, Cauble, RC, Landen, OL, Wark, JS, Ng, A, Rose, SJ, Lewis, CL, Riley, D, Gauthier, Jean-Claude and Audebert, P (2003) Finite temperature dense matter studies on next-generation light sources. Journal of the Optical Society of America B: Optical Physics 20, 770–778.Google Scholar
Lindl, JD, Amendt, P, Berger, LR, Glendinning, SG, Glenzer, HS, Haan, WS, Kauffman, LR, Landen, LO and Suter, JL (2004) The physics basis for ignition using indirect-drive targets on the National Ignition Facility. Physics of Plasmas 11, 339–491.Google Scholar
Liu, CS and Tripathi, VK (2001) Self-focusing and frequency broadening of an intense short-pulse laser in plasmas. Journal of the Optical Society of America A 18, 1714.Google Scholar
Lugiato, LA and Narducci, LM (1985) Single-mode and multimode instabilities in lasers and related optical systems. Physical Review A 32, 1576–1587.Google Scholar
Malkin, VM and Fisch, NJ (2007) Relic crystal-lattice effects on Raman compression of powerful X-ray pulses in plasmas. Physical Review Letters 99, 205001.Google Scholar
Malkin, VM, Fisch, NJ and Wurtele, JS (2007) Compression of powerful x-ray pulses to attosecond durations by stimulated Raman backscattering in plasmas. Physical Review E 75, 026404.Google Scholar
Mahajan, R, Gill, TS and Kaur, R (2010) Nonlinear dynamics of intense EM pulses in plasma. JPCS:IOP 208, 012087.Google Scholar
Manassah, JT, Baldeck, PL and Alfano, RR (1988) Self-focusing and self-phase modulation in a parabolic graded-index optical fiber. Optics Letters 13, 589–591.Google Scholar
Manfredi, G (2005) How to model quantum plasmas. Fields Institute Communications Series 46, 263–287.Google Scholar
Marklund, M and Shukla, PK (2006) Nonlinear collective effects in photon-photon and photon-plasma interactions. Reviews of Modern Physics 78, 591.Google Scholar
Milchberg, HM, Durfee III, CG and Mcllrath, TJ (1995) High-order frequency conversion in the plasma waveguide. Physical Review Letters 75, 2494.Google Scholar
Mourou, GA, Tajima, T and Bulanov, SV (2006) Optics in the relativistic regime. Reviews of Modern Physics 78, 309.Google Scholar
Mulser, P and Bauer, D (2004) Fast ignition of fusion pellets with superintense lasers: Concepts, problems and prospectives. Laser and Particle Beams 22, 5–12.Google Scholar
Na, SC and Jung, YD (2009) Temperature effects on the nonstationary Karpman–Washimi ponderomotive magnetization in quantum plasmas. Physics of Plasmas 16, 074504(1–4).Google Scholar
Neumayer, P, Fortmann, C, Döppner, T, Davis, P, Falcone, RW, Kritcher, AL, Landen, OL, Lee, HJ, Lee, RW, Niemann, C, Le Pape, S and Glenzer, SH (2010) Plasmons in strongly coupled shock-compressed matter. Physical Review Letters 105, 075003.Google Scholar
Neumayer, P, Gregori, G, Ravasio, A, Koenig, M, Price, D, Widmann, K, Bastea, M, Landen, OL and Glenzer, SH (2006) Solid-density plasma characterization with x-ray scattering on the 200J Janus laser. Review of Scientific Instruments 77, 10F317.Google Scholar
Niknam, AR, Barzegar, S and Hashemzadeh, M (2013) Self-focusing and stimulated Brillouin back-scattering of a long intense laser pulse in a finite temperature relativistic plasma. Physics of Plasmas. 20, 122117.Google Scholar
Opher, M, Silva, LO, Dauger, DE, Decyk, VK and Dawson, JM (2001) Nuclear reaction rates and energy in stellar plasmas: The effect of highly damped modes. Physics of Plasmas 8, 2454–2460.Google Scholar
Parashar, J, Pandey, HD and Tripathi, VK (1997) Two-dimensional effects in a tunnel ionized plasma. Physics of Plasmas 4, 3040.Google Scholar
Patil, SD and Takale, MV (2013) Self-focusing of Gaussian laser beam in relativistic cold quantum plasma. Physics of Plasmas 20, 072703.Google Scholar
Patil, SD and Takale, MV (2014) Response to “Comment on ‘Stationary self-focusing of Gaussian laser beam in relativistic thermal quantum plasma’. Physics of Plasmas 21, 064702.Google Scholar
Patil, SD, Takale, MV, Navare, ST and Dongare, MB (2010) Focusing of Hermite-cosh-Gaussian laser beams in collisionless magnetoplasma. Laser and Particle Beams 28, 343–349.Google Scholar
Patil, SD, Takale, MV, Navare, ST, Fulari, VJ and Dongare, MB (2012) Relativistic self-focusing of cosh-Gaussian laser beams in a plasma. Optics and Laser Technology 44, 314.Google Scholar
Patil, SD, Takale, MV, Fulari, VJ, Gupta, DN and Suk, H (2013a) Combined effect of ponderomotive and relativistic self-focusing on laser beam propagation in a plasma. Applied Physics B: Photophysics and Laser Chemistry 111, 1.Google Scholar
Patil, SD, Takale, MV, Navare, ST, Dongare, MB and Fulari, VJ (2013b) Self-focusing of Gaussian laser beam in relativistic cold quantum plasma. Optik 124, 180.Google Scholar
Peyrusse, O, Busquet, M, Kieffer, JC, Jiang, Z and Cote, CY (1995) Generation of hot solid-density plasmas by laser radiation pressure confinement. Physical Review Letters 75, 3862.Google Scholar
Regan, SP, Bradley, DK, Chirokikh, AV, Craxton, RS, Meyerhofer, DD, Seka, W, Short, RW, Simon, A, Town, RPJ and Yaakobi, B (1999) Laser-plasma interactions in long-scale-length plasmas under direct-drive National Ignition Facility conditions. Physics of Plasmas 6, 2072–2080.Google Scholar
Remington, BA, Drake, RP and Ryutov, DD (2006) Experimental astrophysics with high power lasers and Z pinches. Reviews of Modern Physics 78, 755.Google Scholar
Ren, H, Wu, Z and Chu, PK (2007) Dispersion of linear waves in quantum plasmas. Physics of Plasmas 14, 062102.Google Scholar
Saini, NS and Gill, TS (2006) Self-focusing and self-phase modulation of an elliptic Gaussian laser beam in collisionless magnetoplasma. Laser and Particle Beams 24, 447.Google Scholar
Sarkisov, GS, Bychenkov, V.Yu, Novikov, VN, Tikhonchuk, VT, Maksimchuk, A, Chen, S-Y, Wagner, R, Mourou, G and Umstadter, D (1999) Self-focusing, channel formation, and high-energy ion generation in interaction of an intense short laser pulse with a He jet. Physical Review E 59, 7042–7054.Google Scholar
Sharma, A, Verma, MP and Sodha, MS (2004) Self-focusing of electromagnetic beams in a collisional plasmas with nonlinear absorption. Physics of Plasmas 11, 4275–4279.Google Scholar
Shpatakovskaya, G (2006) Semiclassical model of a one-dimensional quantum dot. Journal of Experimental and Theoretical Physics 102, 466.Google Scholar
Shukla, PK and Eliasson, B (2007) Nonlinear interactions between electromagnetic waves and electron plasma oscillations in quantum plasmas. Physical Review Letters 99, 096401.Google Scholar
Shukla, PK and Eliasson, B (2010) Nonlinear aspects of quantum plasma physics. Physics Uspekhi 53, 51–76.Google Scholar
Shukla, PK and Eliasson, B (2011) Nonlinear collective interactions in quantum plasmas with degenerate electron fluids. Reviews of Modern Physics 83, 885.Google Scholar
Shukla, PK, Ali, S, Stenflo, L and Marklund, M (2006) Physics of Plasmas 13, 112111.Google Scholar
Skarka, V and Aleksic, NB (2006) Stability criterion for dissipative soliton solutions of one-, two-, and three dimensional complex cubic quintic Ginzburg-Landau equations. Physical Review Letters 96, 013903-1–013903-4.Google Scholar
Skarka, V, Berezhiani, VI and Miklaszewski, R (1997) Spatiotemporal soliton propagation in saturating nonlinear optical media. Physical Review E 56, 1080–1087.Google Scholar
Skarka, V, Berezhiani, VI and Miklaszewski, R (1999) Generation of light spatiotemporal solitons from asymmetric pulses in saturating nonlinear media. Physical Review E 59, 1270–1273.Google Scholar
Sodha, MS, Ghatak, AK and Tripathi, VK (1974) Self-Focusing of Laser Beams in Dielectric Plasma and Semi Conductors. New York: Tata McGraw-Hill.Google Scholar
Sodha, MS, Ghatak, AK and Tripathi, VK (1976) Self-focusing of laser beams in plasmas and semiconductors. Progress in Optics 13, 171–365.Google Scholar
Sprangle, P, Hafizi, B and Penano, JR (2000) Laser pulse modulation instabilities in plasma channels. Physical Review E 61, 4381–4393.Google Scholar
Subbarao, D, Uma, R and Singh, H (1998) Paraxial theory of self-focusing of cylindrical laser beams. I. ABCD laws. Physics of Plasmas 5, 3440.Google Scholar
Tabak, M, Hammer, J, Glinsky, ME, Kruer, WL, Wilks, SC, Woodworth, J, Campbell, EM, Perry, MD and Mason, RJ (1994) Ignition and high gain with ultrapowerful lasers. Physics of Plasmas 1, 1626–1634.Google Scholar
Takale, MV, Navare, ST, Patil, SD, Fulari, VJ and Dongare, MB (2009) Self-focusing and defocusing of TEM0p Hermite-Gaussian laser beams in collisionless plasma. Optics Communications 282, 3157–3162.Google Scholar
Uhm, HS, Nam, IH and Suk, HI (2012) Scaling laws of design parameters for plasma wakefield accelerators. Physics Letters A 376, 165–168.Google Scholar
Vinko, SM, Ciricosta, O, Cho, BI, Engelhorn, K, Chung, HK, Brown, CRD, Burian, T, Chalpusky, J, Falcone, RW, Graves, C, Hajkova, V, Higginbotham, A, Juha, L, Krzywinski, J, Lee, HJ, Messerschmidt, M, Murphy, CD, Ping, Y, Scherz, A, Schlotter, W, Toleikis, S, Turner, JJ, Vysin, L, Wang, T, Wu, B, Zastrau, U, Zhu, D, Lee, RW, Heimann, PA, Nagler, B and Wark, JS (2012) Creation and diagnosis of a solid-density plasma with an X-ray free-electron laser. Nature 482, 59–62.Google Scholar
Wang, NQ (1990) Chaotic behaviour in an electron-beam plasma. Physics Letters A 145, 29–32.Google Scholar
Winterberg, F (2008) Lasers for inertial confinement fusion driven by high explosives. Laser and Particle Beams 26, 127–135.Google Scholar
Yu, W, Yu, MY, Xu, H, Tian, YW, Chen, J and Wong, AY (2007) Intense local plasma heating by stopping of ultrashort ultraintense laser pulse in dense plasma. Laser and Particle Beams 25, 631–638.Google Scholar
Zare, S, Rezaee, S, Yazdani, S, Anvari, A and Sadighi-Bonabi, R (2015) Relativistic Gaussian laser beam self-focusing in collisional quantum plasmas. Laser and Particle Beams 33, 397.Google Scholar
Zhou, Z, Wang, Y, Yuan, C and Du, Y (2011) Self-focusing and defocusing of Gaussian laser beams in plasmas with linear temperature ramp. Physics of Plasmas 18, 073107.Google Scholar