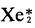Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-28T00:27:24.507Z Has data issue: false hasContentIssue false
  • English
  • Français

Sensitivity analysis of excimer fluorescence generated from charged particle excitation

Published online by Cambridge University Press:  09 March 2009

A. K. Chung  and
M. A. Prelas
A. K. Chung
Affiliation:
University of Missouri–Columbia, Columbia, MO 65211
M. A. Prelas
Affiliation:
University of Missouri–Columbia, Columbia, MO 65211
Get access Rights & Permissions [Opens in a new window]

Abstract

Sensitivity analysis is a powerful first-order mathematical technique that identifies the major reactions, the effects of errors in rate constants, pressure effects, and temperature effects in a plasma chemistry type model. Several methods of sensitivity analysis have been discussed in the literature. This paper describes the successful implementation of the state transition matrix method to the sensitivity analysis of a 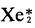plasma chemistry model using both e-beams and ions for excitation. The ion excited plasma study is important to the field of nuclear-pumped lasers. This model examines 8 species and 37 reactions.

Type
Research Article
Information
Laser and Particle Beams , Volume 5 , Issue 1 , February 1987 , pp. 125 - 132
Copyright
Copyright © Cambridge University Press 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Atherton, R. W., Schainker, R. B. & Ducot, E. R. 1975 AIChE J., 21, 441.CrossRefGoogle Scholar
Boody, F. & Prelas, M. 1983 Excimer Lasers-83, AIP Proceeding 110.Google Scholar
Chung, A. K. & Prelas, M. A. 1984 Nucl. Sci. Engr. 86, 267.CrossRefGoogle Scholar
Cukier, R. I., Fortuin, C. M., Shuler, K. E., Petschek, A. G. & Schaibly, J. H. 1973 J. Chem. Phys. 59, 3873.CrossRefGoogle Scholar
Demiralp, M. & Rabitz, R. 1981 J. Chem. Phys. 75, 1810.CrossRefGoogle Scholar
Ducy, C. & Hyman, H. A. 1980 Phys. Rev. A22, 1878.Google Scholar
Ducy, C. & Boness, J. 1980a IEEE J. Quantum Electron. QE-16, 638.Google Scholar
Eckstrom, D. J., Lorents, D. C., Nakano, H. H., Rothem, T., Betts, J. A. & Lainhart, M. E. 1982 Development of Rare Gas Excimer Photolytic Drivers, SRI Intl. Report Number MP 81–82, Menlo Park, California.Google Scholar
Hwang, J. T., Dougherty, E. P., Rabitz, S. & Rabitz, H. 1978 J. Chem. Phys. 69, 5183.CrossRefGoogle Scholar
IMSL 1986 International Mathematical and Statistical Libraries Inc., 6th Floor, NBC Building, Houston, Texas 77092 USA.Google Scholar
Keto, J. W., Gleason, G. E. & Walters, G. K. 1974 Phys. Rev. Lett. 33, 1365.CrossRefGoogle Scholar
Lo, R. H. & Miley, G. H. 1974 IEEE Trans. Plasma Sci. PS-2, 198.CrossRefGoogle Scholar
McCann, K. J. & Flannery, M. R. 1977 Appl. Phys. Lett. 31, 1977.CrossRefGoogle Scholar
Oksam, H. J. & Mittelotadt, V. R. 1963 Phys. Rev. 132, 1445.Google Scholar
Platzman, R. L. 1961 J. Appl. Rad. Isotopes, 10, 110.CrossRefGoogle Scholar
Prelas, M. & Loyalka, S. K. 1981 Progress in Nucl. Energy, 8, 35.CrossRefGoogle Scholar
Prelas, M. & Jones, G. 1982 J. Appl. Phys. 53, 464.CrossRefGoogle Scholar
Rhodes, C. K. 1986 Excimer Lasers, Springer-Verlag, Berlin.Google Scholar
Schaibly, J. H. & Shuler, K. E. 1973 J. Chem. Phys. 59, 3879.CrossRefGoogle Scholar
Schneider, R. & Hohl, F. 1984 Nuclear-Pumped Lasers in Advances in Nuclear Science and Technology, Lewins, J., Becker, M., eds., Plenum Press, New York.Google Scholar
Werner, C. W., George, E. V., Hoff, P. W. & Rhodes, C. K. 1977 IEEE J. Quantum Electron. QE-13, 769.CrossRefGoogle Scholar