Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T19:02:49.641Z Has data issue: false hasContentIssue false
  • English
  • Français

Self-similar two-electron temperature plasma expansion into vacuum

Published online by Cambridge University Press:  20 October 2015

D. Bennaceur-Doumaz ,
D. Bara  and
M. Djebli
D. Bennaceur-Doumaz*
Affiliation:
Centre de Développement des Technologies Avancées, CDTA, B.P. 17, Baba Hassen, 16303 Algiers, Algeria
D. Bara
Affiliation:
Centre de Développement des Technologies Avancées, CDTA, B.P. 17, Baba Hassen, 16303 Algiers, Algeria
M. Djebli
Affiliation:
Theoretical Physics Laboratory, Faculty of Physics, USTHB, B.P. 32 Bab Ezzouar, 16079 Algiers, Algeria
*
Address correspondence and reprint requests to: D. Bennaceur-Doumaz, Centre de Développement des Technologies Avancées, CDTA, B.P. 17 Baba Hassen, 16303 Algiers, Algeria. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A theoretical model is developed to describe self-similar plasma expansion into vacuum with two different electron temperature distribution functions. The cold electrons are modeled with a Maxwellian distribution while the hot ones are supposed to be non-thermal obeying a kappa distribution function. It is shown that ion density and velocity profiles depend only on cold electron distribution in early stage of expansion whereas ion acceleration is mainly governed by the hot electrons at the ion front and is strongly enhanced with the proportion of kappa distributed electrons. 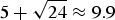It is also found that when the kappa index is decreasing, the critical value of temperature ratio Teh/Tec, limiting the application of quasi-neutrality, becomes larger than the $5 + \sqrt {24} \approx 9.9$ value obtained in the two-electron Maxwellian Bezzerides model [Bezzerides, B., Forslund, D. W. & Lindman, E. L. (1978). Phys. Fluids21, 2179–2185].

Keywords

Ion accelerationKappa distribution functionLaser produced plasmaPlasma expansion into vacuumTwo-electron temperature plasma
Type
Research Article
Information
Laser and Particle Beams , Volume 33 , Issue 4 , December 2015 , pp. 723 - 730
Copyright
Copyright © Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bara, D., Djebli, M. & Bennaceur-Doumaz, D. (2014). Combined effects of electronic trapping and non-thermal electrons on the expansion of laser produced plasma into vacuum. Laser Part. Beams 32, 391–398.CrossRefGoogle Scholar
Beilis, I. (2007). Laser plasma generation and plasma interaction with ablative target. Laser Part. Beams 25, 53–63.CrossRefGoogle Scholar
Beilis, I. (2012). Modeling of the plasma produced by moderate energy laser beam interaction with metallic targets: physics of the phenomena. Laser Part. Beams 30, 341–356.CrossRefGoogle Scholar
Bennaceur-Doumaz, D., Bara, D., Benkhelifa, E. & Djebli, M. (2015). Effects of nonthermal electrons on plasma expansion into vacuum. J. Appl. Phys. 117, 043303.CrossRefGoogle Scholar
Bennaceur-Doumaz, D. & Djebli, M. (2010). Modeling of laser induced plasma expansion in the presence of non-Maxwellian electrons. Phys. Plasmas 17, 074501.CrossRefGoogle Scholar
Bezzerides, B., Forslund, D.W. & Lindman, E.L. (1978). Existence of rarefaction shocks in a laser plasma corona. Phys. Fluids 21, 2179–2185.CrossRefGoogle Scholar
Breizman, B.N. & Arefiev, A.V. (2007). Ion acceleration by hot electrons in microclusters. Phys. Plasmas 14, 073105.CrossRefGoogle Scholar
Bulgakova, N.M., Bulgakov, A.V. & Bobrenok, O.F. (2000). Double layer effects in laser-ablation plasma plumes. Phys. Rev. E 62, 5624–5635.CrossRefGoogle ScholarPubMed
Cheng, J., Perrie, W., Wub, B., Tao, S., Edwardson, S.P., Dearden, G. & Watkins, K.G. (2009). Ablation mechanism study on metallic materials with a 10ps laser under high fluence. Appl. Surf. Sci. 255, 8171–8175.CrossRefGoogle Scholar
Diaw, A. & Mora, P. (2011). Rarefaction shock in plasma with a bi-Maxwellian electron distribution function. Phys. Rev. E 84, 036402.CrossRefGoogle ScholarPubMed
Goldman, M.V., Newman, D.L. & Mangeney, A. (2007). Theory of weak bipolar fields and electron holes with applications to space Plasmas. Phys. Rev. Lett. 99, 145002.CrossRefGoogle ScholarPubMed
Gurevich, A.V., Anderson, D. & Wilhelmsson, H. (1979) Ion acceleration in an expanding rarefied plasma with non-maxwellian electrons. Phys. Rev. Lett. 42, 769–772.CrossRefGoogle Scholar
Gurevich, A.V. & Meshcherkin, A.P. (1981). Ion acceleration in an expanding plasma. Sov. Phys. JETP 53, 937–945.Google Scholar
Gurevich, A.V., PariÏskaya, L.V. & PitaevskiÏ, L.P. (1966). Self-similar motion of rarefied plasma. Sov. Phys. JETP 22, 449–454.Google Scholar
Hairapetian, G. & Stenzel, R.L. (1988). Expansion of a two-electron-population plasma into vacuum. Phys. Rev. Lett. 61, 1607–1610.CrossRefGoogle ScholarPubMed
Hairapetian, G. & Stenzel, R.L. (1991). Particle dynamics and current-free double layers in an expanding, collisionless, two-electron-population plasma. Phys. Fluids B 3, 899–914.CrossRefGoogle Scholar
Hellberg, M.A., Mace, R.L., Armstrong, R.J. & Karlstad, G. (2000). Electron-acoustic waves in the laboratory: an experiment revisited. J. Plasma Phys. 64, 433–443.CrossRefGoogle Scholar
Ivlev, A.V. & Fortov, V.E. (1999). One-dimensional plasma expansion into a vacuum in the field of an electromagnetic wave. Phys. Plasmas 6, 1508–1514.CrossRefGoogle Scholar
Kiefer, T., Schlege, T. & Kaluza, M.C. (2013). Plasma expansion into vacuum assuming a steplike electron energy distribution. Phys. Rev. E 87, 043110.CrossRefGoogle ScholarPubMed
Kovalev, V.F., Bychenkov, V.Yu. & Tikhonchuk, V.T. (2001). Ion Acceleration during adiabatic plasma expansion: renormalization group approach. JETP Lett. 74, 10–14.CrossRefGoogle Scholar
Kovalev, V.F., Bychenkov, V.Yu. & Tikhonchuk, V.T. (2002). Particle dynamics during adiabatic expansion of a plasma bunch. JETP 95, 226–241.CrossRefGoogle Scholar
Krasa, J., Jungwirth, K., Krousky, E., Laska, L., Rohlena, K., Pfeifer, M., Ullschmied, J. & Velyhan, A. (2007). Temperature and centre-of-mass energy of ions emitted by laser-produced polyethylene plasma. Plasma Phys. Control. Fusion 49, 1649–1659.CrossRefGoogle Scholar
Lontano, M. & Passoni, M. (2006). Electrostatic field distribution at the sharp interface between high density matter and vacuum. Phys. Plasmas 13, 042102.CrossRefGoogle Scholar
Mascali, D., Tudisco, S., Gambino, N., Pluchino, A., Anzalone, A., Musumeci, F., Rapisarda, A. & Spitaleri, A. (2012). Prompt electrons driving ion acceleration and formation of a two-temperature plasma in nanosecond laser-ablation domain. Euro. Phys. Lett. 100, 45003.CrossRefGoogle Scholar
Mehdian, H., Kargarian, A. & Hajisharifi, K. (2014). Spatiotemporal evolution of a thin plasma foil with Kappa distribution. Laser Part. Beams 32, 523–529.CrossRefGoogle Scholar
Mora, P. (2003). Plasma expansion into a vacuum. Phys. Rev. Lett. 90, 185002.CrossRefGoogle ScholarPubMed
Mora, P. (2005). Thin-foil expansion into a vacuum. Phys. Rev. E 72, 056401.CrossRefGoogle ScholarPubMed
Mora, P. & Pellat, R. (1979). Self-similar expansion of a plasma into a vacuum. Phys. Fluids 22, 2300–2304.CrossRefGoogle Scholar
Rohlena, K., Kralikova, B., Krasa, J., Laska, L., Masek, K., Pfeifer, M., Skala, J., Parys, P., Wolowski, J., Woryna, E., Farny, J., Mroz, W., Roudskoyji, I., Shamaev, O., Sharkov, B., Shumshurov, A., Bryunetkin, B.A., Haseroth, H., Collier, J., Kuttenbeger, A., Langbein, K. & Kugler, H. (1996). Ion production by lasers using high-power densities in a near infrared region. Laser Part. Beams 14, 335–345.CrossRefGoogle Scholar
Sack, Ch. & Schamel, H. (1987). Plasma expansion into vacuum- a hydrodynamic approach. Phys. Rep. 156, 311–395.CrossRefGoogle Scholar
Sarri, G., Dieckmann, M.E., Kourakis, I. & Borghesi, M. (2010). Shock creation and particle acceleration driven by plasma expansion into a rarefied medium. Phys. Plasmas 17, 082305.CrossRefGoogle Scholar
Shokoohi, R. & Abbasi, H. (2009). Influence of electron velocity distribution on the plasma expansion features. J. Appl. Phys. 106, 033309.CrossRefGoogle Scholar
Tikhonchuk, V.T., Andreev, A.A., Bochkarev, S.G. & Bychenkov, V.Yu. (2005). Ion acceleration in short-laser-pulse interaction with solid foils. Plasma Phys. Control. Fusion 47, B869–B877.CrossRefGoogle Scholar
True, M.A., Albritton, J.R. & Williams, E.A. (1981). Fast ion production by suprathermal electrons in laser fusion plasmas. Phys. Fluids 24, 1885–1893.CrossRefGoogle Scholar
Wickens, L.M. & Allen, J.E. (1979). Free expansion of a plasma with two electron temperatures. J. Plasma Phys. 22, 167–185.CrossRefGoogle Scholar
Wickens, L.M., Allen, J.E. & Rumsby, P.T. (1978). Ion emission from laser-produced plasmas with two electron temperatures. Phys. Rev. Lett. 41, 243–246.CrossRefGoogle Scholar
Wołowski, J., Celona, L., Ciavola, G., Gammino, S., Krása, J., Láska, L., Parys, P., Rohlena, K., Torrisi, L. & Woryna, E. (2002). Expansion of tungsten ions emitted from laser-produced plasma in axial magnetic and electric fields. Laser Part. Beams 20, 113–118.CrossRefGoogle Scholar
Yoon, P.H., Rhee, T. & Ryu, C-M. (2005). Self-consistent generation of superthermal electrons by beam-plasma interaction. Phys. Rev. Lett. 95, 215003.CrossRefGoogle ScholarPubMed
Yu, M.Y. & Luo, H. (1995). Adiabatic self-similar expansion of dust grains in a plasma. Phys. Plasmas 2, 591–593.CrossRefGoogle Scholar
Zel'dovich, Y.aB. & Raizer, Yu.P. (1966). Physics of Shock Waves and High-Temperature Phenomena. New York: Academic Press.Google Scholar