Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Bastykova, N. Kh.
Kodanova, S. K.
Ramazanov, T. S.
and
Moldabekov, Zh. A.
2017.
Over the barrier electron transfer from a micron sized charged dust particle to an ion in gas discharge plasmas.
Physics of Plasmas,
Vol. 24,
Issue. 6,
Kodanova, S K
Ramazanov, T S
Issanova, M K
and
Moldabekov, Zh A
2017.
Software development for the calculation of dynamic properties of dense plasmas: Coulomb logarithm, relaxation and transport properties.
Journal of Physics: Conference Series,
Vol. 905,
Issue. ,
p.
012023.
Moldabekov, Zh A
Ramazanov, T S
Gabdullin, M T
Tikhonov, A
Baigarin, K
and
Kaikanov, M
2017.
Formalism of compound particles for simulation of the heavy ions in a stationary nonequilibrium warm dense matter.
Journal of Physics: Conference Series,
Vol. 905,
Issue. ,
p.
012021.
Cortez, Ross J.
and
Cassibry, Jason T.
2018.
Stopping power in D6Li plasmas for target ignition studies.
Nuclear Fusion,
Vol. 58,
Issue. 2,
p.
026009.
Ramazanov, T. S.
Kodanova, S. K.
Bastykova, N. Kh.
and
Maiorov, S. A.
2018.
Investigation of Hydrodynamic Properties of Hot Dense Plasma.
Physics of Wave Phenomena,
Vol. 26,
Issue. 4,
p.
327.
Ramazanov, Tlekkabul S.
Moldabekov, Zhandos A.
and
Gabdullin, Maratbek T.
2018.
Impact of single particle oscillations on screening of a test charge.
The European Physical Journal D,
Vol. 72,
Issue. 6,
Ramazanov, Tlekkabul S.
Amirov, Samat M.
and
Moldabekov, Zhandos A.
2018.
Impact of quantum non‐locality and electronic non‐ideality on e–He scattering in a dense plasma.
Contributions to Plasma Physics,
Vol. 58,
Issue. 2-3,
p.
155.
Kodanova, S.K.
Ramazanov, T.S.
Khikmetov, A.K.
and
Issanova, M.K.
2018.
Dynamical properties of inertial confinement fusion plasmas.
Contributions to Plasma Physics,
Vol. 58,
Issue. 10,
p.
946.
Kodanova, S.K.
Issanova, M.K.
Amirov, S.M.
Ramazanov, T.S.
Tikhonov, A.
and
Moldabekov, Zh.A.
2018.
Relaxation of non-isothermal hot dense plasma parameters.
Matter and Radiation at Extremes,
Vol. 3,
Issue. 1,
p.
40.
Kodanova, S K
Ramazanov, T S
Issanova, M K
Bastykova, N Kh
Golyatina, R I
and
Maiorov, S A
2018.
Calculation of ion stopping in dense plasma by the Monte-Carlo method.
Journal of Physics: Conference Series,
Vol. 946,
Issue. ,
p.
012014.
Kodanova, Sandugash K.
Issanova, Moldir K.
Ramazanov, Tlekkabul S.
Khikmetov, Askar K.
and
Maiorov, Sergey A.
2019.
Simulation of positronium plasma by the molecular dynamics method.
Contributions to Plasma Physics,
Vol. 59,
Issue. 6,
Ismagambetova, Tomiris N.
Moldabekov, Zhandos A.
Amirov, Samat M.
Ramazanov, Tlekkabul S.
Gabdullin, Maratbek T.
Temirbek, Assem
and
Tikhonov, Alexander
2020.
Dense plasmas with partially degenerate semiclassical ions: screening and structural properties.
Japanese Journal of Applied Physics,
Vol. 59,
Issue. SH,
p.
SHHA10.
Ramazanov, T. S.
Kodanova, S. K.
Nurusheva, M. M.
and
Issanova, M. K.
2021.
Ion core effect on scattering processes in dense plasmas.
Physics of Plasmas,
Vol. 28,
Issue. 9,
Ramazanov, T. S.
Issanova, M. K.
Aldakul, Ye. K.
and
Kodanova, S. K.
2022.
Ion core effect on transport characteristics in warm dense matter.
Physics of Plasmas,
Vol. 29,
Issue. 11,
Dzhumagulova, K. N.
Shalenov, E. O.
Tashkenbayev, Y. A.
and
Ramazanov, T. S.
2022.
Electron–atom interactions in dense semiclassical helium plasma.
Physics of Plasmas,
Vol. 29,
Issue. 1,
Shalenov, Erik O.
Nuraly, Askhat T.
and
Dzhumagulova, Karlygash N.
2022.
Bound states of the hydrogen atom in high‐density plasmas.
Contributions to Plasma Physics,
Vol. 62,
Issue. 10,
Ramazanov, T. S.
Ismagambetova, T. N.
and
Gabdullin, M. T.
2023.
The Influence of the Effects of the Bound Electrons on the Ion Structural and Thermodynamic Properties.
IEEE Transactions on Plasma Science,
Vol. 51,
Issue. 5,
p.
1208.
Moldabekov, Zhandos A.
Pavanello, Michele
Böhme, Maximilian P.
Vorberger, Jan
and
Dornheim, Tobias
2023.
Linear-response time-dependent density functional theory approach to warm dense matter with adiabatic exchange-correlation kernels.
Physical Review Research,
Vol. 5,
Issue. 2,
Yan, Tong
Jiao, Li Guang
Liu, Aihua
Wang, Yuan Cheng
Montgomery, Henry E.
Ho, Yew Kam
and
Fritzsche, Stephan
2024.
Bound state energies and critical bound region in the semiclassical dense hydrogen plasmas.
Physics of Plasmas,
Vol. 31,
Issue. 4,
Djienbekov, N. E.
Bastykova, N. Kh.
Ramazanov, T. S.
and
Kodanova, S. K.
2024.
Non-equilibrium molecular dynamics study of heat transfer parameters in two-dimensional Yukawa systems under uniform magnetic field.
Scientific Reports,
Vol. 14,
Issue. 1,
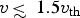 $v\,{\rm \lesssim}\, 1.5 v_{{\rm th}}$, where vth is the thermal velocity of the plasma electrons.
$v\,{\rm \lesssim}\, 1.5 v_{{\rm th}}$, where vth is the thermal velocity of the plasma electrons.