Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-09T07:45:29.220Z Has data issue: false hasContentIssue false
  • English
  • Français

Two Dimensional Analytical Considerations of Large Magnetic and Electric Fields in Laser Produced Plasmas

Published online by Cambridge University Press:  09 March 2009

S. Eliezer  and
A. Loeb Loeb
S. Eliezer
Affiliation:
Institute for Fusion Studies, The University of Texas at Austin, Austin, Texas 78712, U.S.A.
A. Loeb Loeb
Affiliation:
Plasma Physics Department, SOREQ Nuclear Research Center, Yavne 70600, Israel
Get access Rights & Permissions [Opens in a new window]

Abstract

A simple model in two dimensions is developed and solved analytically taking into account the electric and magnetic fields in laser produced plasmas. The electric potential in this model is described by the non-linear differential equation

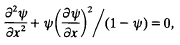
ψ = eφ/T, where eφ is the electric potential energy and T is the temperature in energy units. The physical branch ψ < 1, defined by the electron density n = no exp ψ, boundary conditions n (x = 0) = const and n (x = +∞) = 0, introduces a typical electrostatic double layer. The stationary solution of this model is consistent for − 3 ≲ ψ < 1, with electron temperatures in the KeV region and a ratio of the electric (E) to magnetic (B) fields of [E/106 v/cm]/[B/MGauss] ∼ 1.

Type
Research Article
Information
Laser and Particle Beams , Volume 4 , Issue 2 , May 1986 , pp. 249 - 259
Copyright
Copyright © Cambridge University Press 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alfvén, H. 1981 Cosmic Plasmas (Reidel, Dordrecht).CrossRefGoogle Scholar
Alfvén, H. 1984 Second International Symposium on Double Layers, edited by Schrittwieser, R. (Institute of Theoretical Physics, Innsbruck, Austria).Google Scholar
Biermann, L. 1950 Zs. f. Naturforsh. 5a, 65.Google Scholar
Braginskii, S. I. 1965 Rev. Plasma Phys. 1, 205.Google Scholar
Briand, J., Adrian, V., Tamer, M. El., Gomes, A., Quemener, Y., Dinguirard, J. P. & Kieffer, J. C. 1985 Phys. Rev. Lett. 54, 38.CrossRefGoogle Scholar
Cicchitelli, L., Elijah, J. S., Eliezer, S., Ghatak, A. K., Goldsworthy, M. P., Hora, H. & Lalousis, P. 1984 Laser and Particle Beams 2, 467.Google Scholar
Donaldson, T. P., Lädrach, P. & Wägli, P. 1979 Phys. Lett. 70A, 419.CrossRefGoogle Scholar
Eliezer, S. & Ludmirsky, A. 1983 Laser and Particle Beams, 1, 251.CrossRefGoogle Scholar
Forslund, D. W. & Brackbill, J. U. 1982 Phys. Rev. Lett. 48, 1614.Google Scholar
Gautschi, W. & Cahill, W. F. 1972 Handbook of Mathematical Functions, Ed. Abramowitz, M. and Stegun, I. A. (Dover Pub., New York) p. 228.Google Scholar
Hershkowitz, N. 1985 ‘Review of Recent laboratory Double Layer Experiments,’ to be published in Space Science Review.CrossRefGoogle Scholar
Hora, H. 1975 Laser Plasma and Nuclear Energy (Plenum, New York),Google Scholar
Hora, H., Lalousis, P. & Eliezer, S. 1984 Phys. Rev. Lett. 53, 1650.Google Scholar
Hora, H. 1985 Laser and Particle Beams, 3, 59.Google Scholar
Key, M. H. 1980 Laser Plasma Interactions (Proceedings of the Twentieth Scottish Universities Summer School in Physics, St. Andrews) Ed. Cairns, R. A. and Sanderson, J. J., p. 219.Google Scholar
Kolodner, R. & Yablonovitch, E. 1979 Phys. Rev. Lett. 43, 1420.Google Scholar
Lalousis, P. & Hora, H. 1983 Laser and Particle Beams, 1, 283.Google Scholar
Levine, J. S. & Crawford, F. W. 1980 J. Plasma Phys. 24, 359.Google Scholar
Ludmirsky, A., Eliezer, S., Arad, B., Borowitz, A., Gazit, Y., Jackel, S., Krumbein, A. D., Salzmann, D. & Szichman, H. 1985 IEEE Transactions on Plasma Science, 13, 132.Google Scholar
Max, C. E., Manheimer, W. M. & Thomson, J. J. 1978 Phys. Fluids, 21, 128.Google Scholar
Max, C. E. 1982 Laser-Plasma Interaction, ed. Balian, R. and Adam, J. C., Les Houches Summer School Proceedings Vol. 34 (North Holland, Amsterdam).Google Scholar
Mendel, C. W. & Ohlsen, J. N. 1975 Phys. Rev. Lett. 34, 859.Google Scholar
Mora, P. & Pellat, R. 1981 Phys. Fluids, 24, 2219.Google Scholar
Ramani, A. & Laval, G. 1978 Phys. Fluids, 21, 980.Google Scholar
Raven, A., Willi, O. & Rumsby, P. T. 1978 Phys. Rev. Lett. 41, 554.CrossRefGoogle Scholar
Sato, N., Hatakuyama, R., Iizuka, S., Mieno, T., Saeki, K., Rasmussen, J. & Michelson, P. 1981 Phys. Rev. Lett. 46, 1330.CrossRefGoogle Scholar
Stamper, J. A., Papadopoulos, K., Sudan, R. N., Dean, S. O., McLean, E. A. & Dawson, J. M. 1971, Phys. Rev. Lett. 26, 1012.Google Scholar
Stamper, J. A. & Tidman, D. A. 1973 Phys. Fluids, 16, 2004.CrossRefGoogle Scholar
Stamper, J. A. 1975 Phys. Fluids, 18, 735.CrossRefGoogle Scholar
Stamper, J. A. 1976 Phys. Fluids, 19, 758.Google Scholar
Stamper, J. A., McLean, E. A. & Ripin, B. H. 1978 Phys. Rev. Lett. 40, 1177.CrossRefGoogle Scholar
Stenzel, R. L., Ooyama, M. & Nakamura, Y. 1981 Phys. Fluids, 24, 708.CrossRefGoogle Scholar
Tidman, D. A. & Shanny, R. A. 1974 Phys. Fluids, 17, 1207.Google Scholar
Towen, S. & Lindberg, L. 1980 J. Phys. D, 13, 2285.Google Scholar
Yates, M. A., Van Hulstein, D. B., Rutkowski, H., Kirala, G. & Brackbill, J. U. 1982 Phys. Rev. Lett. 49, 1702.Google Scholar