1 Introduction
1.1 Delay discounting, time preference, and what this survey is and is not.
People are constantly making decisions that involve whether they take gains (also losses) now or at some later time(s). How people actually achieve this, either as individuals or collectively as a segment of an economy, is an active area of research that straddles the boundaries of psychology, economics, marketing, decision analysis, and more recently neuroscience. It goes by several names, some generally preferred by psychologists (delay discounting), others by economists (time preference). Although widely applicable, this survey will limit itself to delay discounting for simple financial decisions, not just because these are an important class of problems that people face, but also for clarity of presentation. The same models may be used in non-financial applications.
The following are examples that illustrate this claim in the context of consumer research. Reference Estle, Green, Myerson and HoltEstle, Green, Myerson, and Holt (2007), for instance, compared monetary with consumable rewards (candy, soda, beer), finding that the latter were discounted more steeply. Reference Chapman and ElsteinChapman and Elstein (1995), used formal models of delay discounting where rewards were presented as days on vacation (and years of health in another experiment). Others have focused on impulsivity as a personality trait, a theme particularly researched in the area of out-of-control consumption behaviors such as drug addiction, smoking, gambling, alcoholism, and so on (Reference Madden and BickelMadden & Bickel, 2009); but also in discounting’s more prosaic connection with numerical ability (Reference Peters, Slovic, Västfjäll and MertzPeters, Slovic, Västfjäll, & Mertz, 2008). Focusing on the situation (i.e., the kind of commodity being discounted) rather than the person, other researchers have examined the extent to which discounting is domain specific in normal (i.e., non-addicted) people who nonetheless also experience the temptations of consumption (Reference Hardisty and WeberHardisty & Weber, 2009; Reference Tsukayama and DuckworthTsukayama & Duckworth, 2010; Reference Weatherly, Terrell and DerenneWeatherly, Terrell, & Derenne, 2010). Yet others have examined factors that lead people to behave more impulsively across disconnected domains: e.g., Reference Wilson and DalyWilson and Daly (2004) found that seeing pictures of the faces of attractive women induced men to discount money more steeply than if the faces were unattractive. Reference Van den Bergh, Dewitte and WarlopVan den Bergh, Dewitte, and Warlop (2008) reached similar conclusions for men who were asked to handle bikinis. However, the precision with which these diverse examples may be understood depends on the accuracy of the models that are used to measure delay discounting. Because these models lie scattered in many different literatures, even researchers who are active in the field may be unaware of interesting new developments, which is one value of this survey.
The most general principle in delay discounting is that people prefer to be given money now rather than later, so that in subjectively valuing timed rewards, future payments are described as being discounted (by the fact of being delayed). This paper is a survey of delay discounting models. It would have been a brief survey, in that none of the models is examine in great depth, were it not for the large number of models that exist in the literature. Although presented from the perspective of gains, each model may also be applied to losses. To keep the survey slim I have generally not amplified where and how the models have been used, nor with what success. Nor have I surveyed empirical comparisons between models, because apart from comparisons between Hyperbolic and Exponential, and between quasi-Hyperbolic and Exponential, the literature contains few face-to-face comparisons.
Furthermore, whether a model is considered viable often depends on the discipline of the researcher (economists are much more likely to adhere to the Exponential model than psychologists). Viability may also depend on any of the following: individual differences—whether correlates of those difference are identifiable, such as the level of numeracy of the person, or not ; whether losses or gains are being considered; the method of elicitation—sometimes the basis of economists’ arguments against non-exponential models (e.g., Reference Andersen, Harrison, Lau and RutströmAndersen, Harrison, Lau, & Rutström, 2011); the culture in which the problem is posed; the nature of the choices being offered (money, bottles of beer, years of health); experimental manipulations—for instance that might make differences versus ratios salient.
Other interesting and important themes that I largely ignore are: the cognitive processes that people would need to achieve in order to discount in a particular way; the efficacy of using multi-item choice questionnaires (Reference Kirby and MarakovicKirby & Marakovic, 1996) compared with simple matching (Reference Smith and HantulaSmith & Hantula, 2008), a hybrid of the two (Reference Rachlin, Raineri and CrossRachlin, Raineri & Cross, 1991), or even reaction times (Reference Chabris, Laibson, Morris, Schuldt and TaubinskyChabris, Laibson, Morris, Schuldt & Taubinsky, 2008); the design of stimuli to improve statistical power to detect differences between models (Reference Doyle, Chen and SavaniDoyle, Chen & Savani, 2011); measurement of model goodness-of-fit and impulsivity (Reference Myerson, Green and WarusawitharanaMyerson, Green & Warusawitharana, 2001; Reference Wileyto, Audrain-McGovern, Epstein and LermanWileyto, Audrain-McGovern, Epstein & Lerman, 2004; Reference Doyle and ChenDoyle & Chen, 2012); how models should be compared (Reference KilleenKilleen, 2009; Reference Doyle and ChenDoyle & Chen, 2012); the parallels between risky choice and intertemporal choice (Reference Prelec and LoewensteinPrelec & Loewenstein, 1991; Reference MyersonGreen & Myerson, 2004; Reference RachlinRachlin, 2006). The paper escapes being a mere catalogue, in that I have aimed to make the structure of the models transparent, comparing them through their mathematics and what implications each has if taken seriously as a model of human behavior. Having disassembled the models into their component parts, I emphasize their role as building blocks by showing how it is possible to re-assemble the components to create novel, speculative models: a process that future researchers may continue.
The paper has the following structure. The introduction argues for a new focus in delay discounting in terms of rate parameter (Section 1.2); describes power laws, log laws, and related mathematical issues (Section 1.3); and the conventions of notation to be adopted (Section 1.4). Sections 2 through 5 describe delay discounting models with zero through three free parameters, respectively. Section 6 describes models not easily classified elsewhere. Section 7 provides a retrospective grouping of models into families, and shows how speculative models may be generated. Conclusions are in Section 8.
1.2 Orientation: discount functions or rate parameter?
There are two strategies for presenting discounting models. In one, a choice between P (present choice) now and F (future choice) later, it is presumed that the F is discounted to its net present value (NPV) and compared with P, and people choose F if its discounted value is greater than P. This is the usual view, from which “delay discounting” “time discounting” or “temporal discounting” take their name. It focuses attention on the discount function that maps an F into a P. In simple models F is multiplied by a discount factor, which is a particular realization of the discount function for a given time delay, to derive the notionally equivalent P that should make a decision maker indifferent between F and P.
An alternative strategy is to rearrange the discounting equation and focus on the rate parameter implied by a given discounting model (e.g., in the exponential model, the rate parameter is the continuously compounded interest rate that would make a P now into an F at time T). This survey adopts the rate parameter view. The advantages are that the components of the discounting model are now quite transparent: how the model treats money, how the model treats time, and how the treated time and money are composed into the final formula. Discount factors increase monotonically with rate parameters, so there is no conflict between the two views in terms of the preference ordering they compute for a set of choices. In the rate parameter view, people are presumed to have, at least during testing, a stable internally held rate that acts as a decision criterion: people choose F if, relative to P, F implies a higher rate than that criterion rate. Seen in this way, rate parameters are also decision parameters. People who are impulsive are identified by having high internal criterion rates. One discounting model is preferred over another as an account of behavior if it more correctly estimates the preference order of the choices on offer. There seems no prior reason to prefer the discounting view over the rate parameter view, or vice versa. Therefore, one task for future research is to determine whether people adopt a discounting view or rate parameter view of intertemporal problems, or indeed another view. Although the views are mathematically equivalent, in bringing certain aspects of the problem to the fore while pushing other aspects into the background, different views may not be psychologically equivalent in terms of the kinds of mental operations required to run a model, the heuristics that might be used to short-cut full computation, and therefore the typical kinds of deviations that people would produce from their true intentionsFootnote 1.
In this survey I classify models somewhat superficially by the number of additional free parameters that an experimental design would need to estimate over and above the rate parameter. I build up the complexity of the models. In the end, however, I am able to show that most models belong to a few families, from which simpler models are special cases. I also speculate on future models.
1.3 Stevens, Weber, powers, logs, ratios, differences, and started time
Most of the models described in this survey can be classified by their treatment of three main issues: (i) (how) is the subjective perception of money to be treated; (ii) (how) is the subjective perception of time to be treated; and (iii) (how) is money to be traded-off against time? In deciding these questions, I will be making repeated use of a few psychological principles and related mathematical relationships. Though they appear throughout the paper, it is worth collecting them together before I begin.
1.3.1 Stevens versus Weber
A long-standing debate in psychology has been whether basic psychophysical phenomena such as the subjective brightness of light, heaviness, sound, pain are best modeled by using logs or powers. The Weber-Fechner “law” dates back to the 18th century and promotes a log treatment. The law assumes that the subjective change in a stimulus (Δ S) has a constant relation with the change in objective energy (Δ E) of a stimulus relative to the existing energy (E).
As an example, many candles will be needed at noon on a sunny day to give the same subjective increase in brightness experienced by lighting a single candle at twilight. Integrating, we have
which is the Weber-Fechner law: Weber associated with form (1), Fechner with form (2). (Log base e is assumed throughout this paper.) Its main challenger is the power “law”, which instead suggests that:
where c depends on the context. For instance, Reference StevensStevens (1957; 1961) documented different power laws for different psychophysical phenomena. Subjective loudness is proportional to (objective sound pressure).67, whereas subjective pain is proportional to (electrical shock to finger)3.5, and so on. It is worth noting that in Wikipedia’s entry for Stevens’ Power Law, there is an approximately even split between exponents > 1, and exponents < 1. The models surveyed in this paper assume that the abstract concepts of time and money (and even time intervals) may be treated in the same way as physical stimuli, by using either Weber’s Law or Stevens’ Power Law. Reference EislerEisler’s (1976) comprehensive review of studies spanning a hundred years settled on a Stevens power exponent for time perception of c ≃ .9. Classical economics, for instance, expects a decreasing marginal utility of money and therefore that the exponent should be < 1. Surveying his own and others’ work Reference StewartStewart (2009) noted a stable exponent for money that was just under .5, i.e. approximately a square root law.Footnote 2
1.3.2 Powers and logs (Stevens ⊇ Weber-Fechner?)
Undoubtedly Stevens’ power law is more flexible than the Weber-Fechner log law, though at the expense of having to estimate an additional parameter. If c = 1 we are treating time or money as if objective. As c decreases towards zero, Ec becomes more curved, in fact more logarithmic-like. This follows from a mathematical result that is important for this paper, which is that if x > 0:
In many applications that compute relative differences (including here) constant scaling factors do not matter just as long as they are applied to all observations. Consequently, the c in the denominator can usually be ignored. Therefore for small c > 0, xc becomes log-like around 1, rather than around 0, as is normal. Therefore, by subtracting 1 from xc, we can morph from linear through fractional power to log, under the control of the parameter c. This is very useful.
The equation y = (xc – 1 ) / c is none other than the Box-Cox transformation, much used in statistics to find suitable functional forms for the relationship between x and y (Reference Box and CoxBox & Cox, 1964). As Reference WakkerWakker (2008) has noted in his useful tutorial on power functions, researchers often neglect to explore the space of c < 0, which gives rise to reciprocal powers. For instance, c = –1 gives the functional form: y = 1 – 1/x. In his Section 2.1 he gives a cautionary example of failing to analyse c < 0.
Sometimes it doesn’t matter whether we subtract 1 or not. For instance, often we are interested in difference relationships such as v = (xc – yc). In this particular case, the Stevens’ Power Law nests the Weber-Fechner Log Law as a special case. This follows because we can re-write the equations as:
then using the mathematical result,
Therefore in order to build in modeling flexibility, rather than forcing a relationship to be log(x/y) and thus fixing on a Weber-Fechner law, we can let it be the more general xc – yc and let an optimizing program determine which c best fits the empirical data. If c is close to zero, then a Weber-Fechner-like log law applies, if c is close to 1, then x and y are linear, if c = .5, then we have a square-root law, and so on.
Sometimes it does matter. For instance, when a single variable is being considered, xc → 1 as c → 0, which implies that the x variable is redundant. In order to avoid this problem, and to be consistent with the log behavior of (xc – yc), the form (xc – 1)/c is often used to express powers, instead of xc.
1.3.3 Started values
Unfortunately, it may happen that x takes the value 0, either always or sometimes. Typically this happens when an amount of money is offered now (at t = 0) compared with an amount offered later. This is then a problem, because log(0) is undefined. The problem also occurs for any power law whose exponent is negative (e.g., t−1 = 1/t is also undefined for t=0). So, any model that wants to treat time as logarithmic, either explicitly or implicitly as the limit of a power law, throws up an anomaly for t = 0, which is actually the most frequently used value of t. One way out of this difficulty is to present t = 0 as a special (sometimes absent) case. Another is to use “started time” instead of time itself. Started counts, started reciprocals, started logs, etc. were recommended by Reference TukeyTukey (1977) and Reference Mosteller and TukeyMosteller and Tukey (1977) to overcome just this kind of problem when dealing with troublesome zeros. Started time translates all measurements t into t + ε, where ε is small relative to the values that t will take. Equivalently, in our calculations we can translate time from days, as may have been stated in the questionnaire, into hours (or even minutes), and just let ε = 1. Under this translation, t = 0 would become t* = 1; t = 2 days would become t* = 49; 7 days would become t* = 169 (all started hours), and so on, with the * subscript emphasizing that we are dealing with started time. Although this tweak is motivated by avoiding a mathematical problem, started time may pragmatically reflect reality better than the nominal time appearing on the questionnaire; because when a reward is offered “now” participants would not assume they would get the reward instantaneously, rather that they would get it after the experiment was over—i.e., quite possibly about an hour later. This delay between mathematical and actual now is even more apparent if the amount is offered “today”.
Reference Ainslie and HerrnsteinAinslie and Herrnstein (1981, p.480) make a similar point, distinguishing between the nominal and effective timing of reinforcements: “It could be argued that the usual convention of measuring delay from a subject’s [pigeon’s] peck to the elevation of the feeder should be abandoned in favor of the interval from the peck until actual eating takes place, or even until the food enters the subject’s bloodstream. The ‘true’ moment of reinforcement is not known and might not even exist as a distinct instant…“ However, researchers have not yet taken up the challenge contained in the last sentence, which is to model the timing of events fuzzily rather than as discrete points.
Generally there should not be a parallel issue for modeling money because in any realistic choice F and P will both be non-zero. If it ever did become an issue, money could similarly be “started” by adding one cent to both P and F.
1.3.4 Treatment of time and money.
In almost all models surveyed here money and time are combined multiplicatively. A ratio is formed between the subjective value of additional money and the subjective dis-value of additional delay: that ratio is the rate parameter. We can distinguish two very general views on time and money. In one, money and time are seen as qualitatively distinct, which means that treating them differently is not an issue. For instance, money can be compounded or subject to inflation, which thus change its face value and/or its real worth: time cannot. Money is traded: time is generally not, and so on. In the other view subjective perceptions of money and subjective time are modeled as if they were standard psychophysical stimuli (pain, brightness, loudness, etc.). Now if psychophysics itself treats its stimuli via consistent functional forms, for instance by Stevens’ power law (or the Weber-Fechner law), it sets a strong precedent for treating time and money via similar functional forms. Accordingly, if a model treats subjective time and money inconsistently, the burden of proof should be on the model’s creator to justify why it does so.
Using the convention that F is offered at time T, and f is offered at time t, with T > t (see Section 1.4: f is known as P as the special case when t = 0), also that a, b, A and B are exponents of the model, used in different ways, the following pairs do not have similar functional forms:
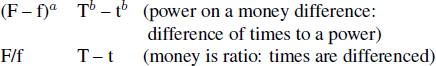
whereas the following do:
This is not to suppose that the parameters need match up (e.g. that A = B, and a = b in these examples). We propose that a useful characteristic to observe in a model is whether it treats time and money symmetrically or not. If it does not, has any special justification been given why not?
1.4 A note on notation.
In defining parameters for the different models, I have tried to obey the following guidelines. I obey common usage where it is standard in general algebra (e.g., r is the common ratio of a Geometric Progression, d the common difference of an Arithmetic Progression). I have tried to use mnemonic devices (e.g., h for hyperbolic, m for the exponent on money), and use capital letters for the models themselves (e.g. E for the exponential model, H for the simple hyperbolic). Generally speaking the rate parameter is lowercase of the uppercase model: e.g., H, h. I have also respected past literature where terminology is widely and standardly used so that it would be confusing to do otherwise (β -δ of the quasi-hyperbolic model). I have tried to use Roman letters (but not e, l, o, or p), rather than Greek. Because of the sheer number of parameters used in this survey, inevitably I have failed. I have used the convention that F is a future gain, and P is the present gain, which follows standard practice in accounting and finance, though not elsewhere. Where I wish to contrast two gains in the future, I have used the symbol f to refer to the less distant one. Thus, because of the premise that people discount delays, generally F > f. To carry the capitalization mnemonic into time, I have used T to refer to more distant time than t (T > t). So, a typical choice might be to ask which alternative is preferred: (f at time t) or (F at time T). Although that may seem quite natural, one awkward consequence of this usage is that, since most models are based around the special case of t=0, the standard symbol for time becomes T, rather than the more natural t. Also, because both t and T are now in use, to maintain mnemonic value I have resorted to using the Greek τ (tau) to subscript parameters and models that focus on a time issue, as well as for exponents used to deform objective time into subjective time. Consequently, we have the presbyopic nightmare of: Tτ and tτ. Old eyes be warned!
Table 1 is provided to help with the many symbols. Note also the legend.
Table 1: Model names, notation used throughout this article, and rate parameter equations.
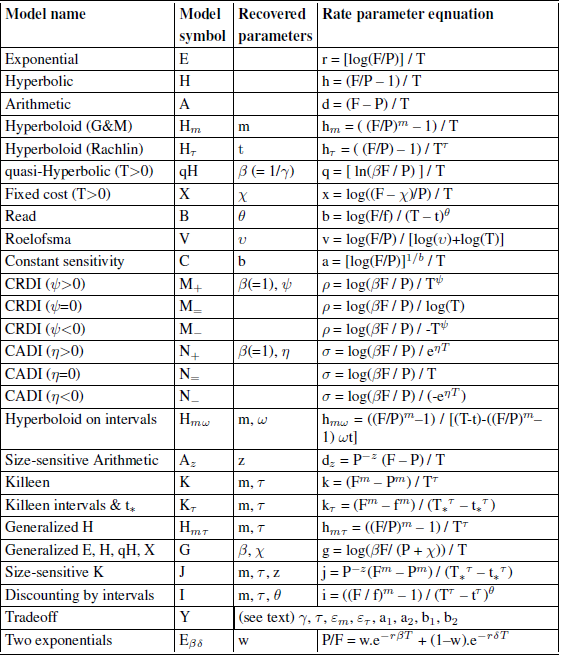
Notes: m is the money exponent.
τ (tau) is the time exponent.
β is the quasi-hyperbolic non-present scaling parameter, and γ = 1/ β is the present-premium.
z is the size exponent in J.
θ is the interval exponent in I (DBI).
F (future value) is the more distant future amount delivered at time T.
f is the less distant amount delivered at time t. If t= 0, f = P, the present value.
T* and t* are “started” times (Tukey).
W and w are weights placed on different processes.
2 Simple rate parameter models
In accounting and finance, discounting can be described either as a method of valuing a future cash flow (F) as a present value (P); or in terms of the Internal Rate of Return (IRR) that would generate F from P. Present values may be used in preference to IRR to consolidate several future cash flows at different times into a single net present value (NPV). However, for simpler problems IRR is often used as a threshold or “hurdle rate” to make investment appraisals (Reference RyanRyan, 2007), and it is the IRR view of the problem which turns out to be more useful for this survey. The very reasons that organizations use an IRR hurdle rate (because it is a single, unambiguous decision criterion that is easy to understand and apply organization-wide by its decision makers), are the same arguments to suggest why lay-people may spontaneously adopt a similar view of intertemporal choice (ITC). Typical ITC problems in the psychological literature do not require people to consolidate several future cash flows, for which NPV comes into its own, so both IRR and NPV are candidates. Note, however, that NPV is a relatively recent invention in accounting, and not one that people in business spontaneously and repeatedly re-invented as a kind of common sense, despite centuries of dealing with relevant problems (Reference RubinsteinRubinstein, 2003). The non-obvious nature of NPV therefore suggests that lay people might be more likely to adopt an IRR view of ITC problems than an NPV one, a hypothesis that deserves empirical investigation. We generalize the concept of IRR from r, the interest rate in E, to cover model rate parameters which capture the intensity of discount operating in each of the other models we consider.
2.1 Exponential discounting (E, r)
The standard financial method of summarizing growth rates by which to translate present values into future values and vice versa is by a geometric mean taken on the ratio of increase. Thus, the compounding growth model for discrete time is:
with F (future value), P (present value), r (growth rate) and T (compounding periods) taking their usual meanings, so that
As an example, if $200 (P) becomes $400 (F) over a period of 4 years (T), then r = (400/200)(1/4) – 1 = .19, or a 19% increase per annum. We can also compute P as:
where [1 / (1 + r)]T is known as the discounting factor: it allows us to translate a future cash flow into its present value. When faced with a choice between:
-
(1) P, an instantaneous payoff now, and
-
(2) F at time T,
the decision maker, operating normatively as an exponential discounter, would apply the discounting factor to F using a given r, and choose the larger of P and the discounted F. Another way of describing this process is to focus on equation (8) and compute r for a given choice of P, F, and T. This is equivalent to the internal rate of return (IRR) as used by accountants, for instance to judge whether a planned project will meet a criterion level of return. If r exceeds a given criterion rate r0, then the accountant would accept F. We posit that r0 is not a commercially available rate of return, but a person-specific one. Each person uses their own r0 as a criterion rate of return by which to judge whether r, computed from choice {P, F, T}, exceeds criterion (hence choose F) or not (hence choose P). We do not, however, claim that r0 is impervious to context, manipulation, and simple fluctuation with time.
If we increase the number of compounding periods to be n per annum, equation (9) becomes:
and if n increases without limit so that compounding is continuous, this becomes
The discount factor therefore becomes e−rT, hence the name “exponential discounting”, though the geometric form in (10) is often still used. The growth rate parameter r is determined from (11) as:
In practice, the exponential and geometric view of growth and discounting do not differ much in their computed values of r. In the above example, equation (12) gives r = 17%, rather than the previously calculated 19% from equation (8).
2.2 Hyperbolic discounting (H, h)
Accountants also frequently calculate the (arithmetic) average rate of return (Reference RyanRyan, 2007, p. 12). Similarly, if a quantity increases by x% over T years, then the arithmetic average of the rate of return should be (x/T)%. In the example cited above there was a 100% increase, which averages out to 25% per annum. Although frequently used to appraise investments and set a benchmark figure for project acceptance, this figure cannot be used in the compound growth formula. Instead of doubling the original as required by a 100% increase, its use would lead to a calculated increase of (1.254 = 2.44) times the original. These arithmetic calculations are equivalent, in algebra, to computing a growth rate of h by:
In the example given in 2.1, h = (2 – 1) / 4 = .25. Equation (13) also implies:
According to equation (14), the discount factor [1 / (1 + hT)] has a hyperbolic form, hence the name “hyperbolic discounting.” Also, whereas E is underpinned by a model of compound interest, H is underpinned by a model of simple interest, with no compounding (Reference RachlinRachlin, 2006). This is also apparent if we let n → 1/T in equation (10) for a single compounding period, which reduces to the hyperbolic model. Thus discrete-time compounding is a half-way house between the extremes of E and H under the control of the frequency of compounding, n. When n is extremely large, the compounding periods become very small, until in the limit we have continuous compounding (therefore E). When n=1, the interest is accrued at the end of the investment period, so in effect we have simple interest (therefore H).
The fact that the 2.44 exceeds 2 (and 25% exceeds 19%) in the above example is no accident, and is due to the mathematical relationship that the arithmetic mean ≥ geometric mean for positive numbers. It follows that, in the period up to T, hyperbolic discounting (which uses the arithmetic mean) will always make a higher estimate of future growth than exponential discounting: therefore, the immediate future will be discounted more heavily in the hyperbolic model. After T, the situation reverses.
We can also use equation (13) to determine the hyperbolic discounting rate parameter h, implicit in any choice {P, F, T}, which we then use to compare against someone’s internal h0. As with exponential discounting, if people apply a hyperbolic model, then if h > h0 they will choose F; if h < h0 they will choose P.
Although the hyperbolic discounting model in equation (14), given in Reference Mazur, Commons, Mazur, Nevin and RachlinMazur (1987), is the one most widely used in current research, it is founded on models that pre-date this formulation. As reviewed in Reference AinslieAinslie (1975), Reference Chung and HerrnsteinChung and Herrnstein’s (1967) found that the rate at which pigeons would peck was proportional to the reciprocal of the time delay, as an instance of the “matching law”. This led Ainslie to propose the first hyperbolic model, presented in Reference Mazur, Commons, Mazur, Nevin and RachlinMazur (1987) as: P = F / kT, where k is a constant of proportionality. The problem with this formulation is that as T → 0, the present value of any reward becomes infinite, but can be remedied by adding a constant to the denominator (Reference Herrnstein, Bradshaw and LoweHerrnstein, 1981), and it is then a short step to fix that constant as the value 1.
Finally, note that the word “hyperbolic” is often used loosely to cover any discounting in which the discount rate is higher at shorter delays than it is at longer delays. We use the term more precisely to refer to the particular model described in (13) and (14).
2.3 Arithmetic discounting (A, d)
In arithmetic discounting, future and present values are compared by constant increments d, exactly as in an arithmetic progression:
Instead of multiplying F by a discount factor to yield P, we subtract a discount decrement (Td). In one choice people are offered P: in the second they are offered P + (F – P). If the participant decomposes the choice in this way, then the decision is whether it is worth waiting for the excess (F – P). If they feel their time is worth d0 per day to wait, then if (F – P) > Td0 they chooses F. Whereas r and h are dimensionless, being essentially expressions of interest rates, d is measured in units of money per time (e.g. dollars per day).
There is another justification for equations (15) and (16). Reference KilleenKilleen (2009) started
from the assumption that the marginal change in utility with respect to time
follows a power law; also, that utility and value are themselves related by a
power law. Taken together these were shown to yield an equation of the form:
![]() (Reference KilleenKilleen, 2009, equation 6, p.605). We examine the general form of this equation in a
later section (4.1). But for now, notice
that if c = 1, subjective time is objective time; and that if k = 1, the utility
of money is just its face value, giving equation (16). Reference Doyle and ChenDoyle and Chen
(2012) found empirical support for A, relative to E and H, both in
other researchers’ past data, and in their own. They surmised that people
were treating delay discounting by analogy with “wages for
waiting” rather than by analogy with “investment growth” as
implied by E and H.
(Reference KilleenKilleen, 2009, equation 6, p.605). We examine the general form of this equation in a
later section (4.1). But for now, notice
that if c = 1, subjective time is objective time; and that if k = 1, the utility
of money is just its face value, giving equation (16). Reference Doyle and ChenDoyle and Chen
(2012) found empirical support for A, relative to E and H, both in
other researchers’ past data, and in their own. They surmised that people
were treating delay discounting by analogy with “wages for
waiting” rather than by analogy with “investment growth” as
implied by E and H.
3 Rate parameter + 1 models
Each of the models in this section has one additional (free) parameter that must be estimated (“recovered”) from the data. The next sub-section 3.1.1, for instance, models utility of money with a power law. An additional parameter offers the possibility of more accurately modeling behavioral discounting, and of also “recovering” additional information, such as how money is subjectively perceived, as captured in the exponent used in Section 3.1.1. But additional parameters also need additional data to avoid the problems of over-fitting; and this data must be distributed to provide sufficient variety in order to estimate the additional parameter.
3.1 Hyperboloid models
3.1.1 Green and Myerson (Hm, hm; m)
Reference Myerson and GreenMyerson and Green (1995) proposed a model which generalizes the hyperbolic. Whereas in this and other publications these authors consistently use the symbol s for the exponent, we use 1/m for consistency with the rest of this article. Their model is:
This model is a special case of Loewenstein and Prelec’s (1992) generalized hyperbola formulation. Further simplifying, if m = 1, we have the hyperbolic. When 1/m (=s) < 1 the tendency of H to discount more steeply than E at short durations (but less so over longer durations) is exaggerated. Equation (17) may be re-arranged to give a rate parameter that is the equivalent of r, h, or d:
The subscript m on the rate parameter emphasizes that money may be treated subjectively, and requires the researcher to estimate m (=1/s) empirically. Typical values that are reported in the literature for s (=1/m) are in the range [.45, .78] (Reference McKerchar, Green, Myerson, Pickford, Hill and StoutMcKerchar, Green, Myerson, Pickford, Hill, & Stout, 2009; Reference McKerchar, Green and MyersonMcKerchar, Green & Myerson, 2010), and these authors find that modeling the additional parameter leads to statistically significant improvements in fit over the hyperbolic. Notably, s is typically less than 1, which means that the ratio (F/R) in equation (18) is being raised to a power greater than 1, thus acting to exaggerate the relative difference between F and P in calculating h m. At the other extreme, when s becomes large, the exponent acts to shrink the ratio (F/R) towards 1, and in so doing (18) begins to approximate the exponential model.
To see why, we use the mathematical relationship that ![]() as c
→ 0. Here x is (F/P) and c is m. The smaller m becomes, the closer
(F/P)m -1 comes to m.log(F/P). Once the
value of m is fixed at some small value, all calculations in (18) are multiplied by the
same m, which in this way just acts as a scaling
constant, and can be ignored. It follows that the exponential model is a
special case of (18) when s
gets to be very large. The take-home point is that since m > 1 in
empirical data, actual behavioral discounting is not a compromise between E
and H, but lies even further from E than H had suggested.
as c
→ 0. Here x is (F/P) and c is m. The smaller m becomes, the closer
(F/P)m -1 comes to m.log(F/P). Once the
value of m is fixed at some small value, all calculations in (18) are multiplied by the
same m, which in this way just acts as a scaling
constant, and can be ignored. It follows that the exponential model is a
special case of (18) when s
gets to be very large. The take-home point is that since m > 1 in
empirical data, actual behavioral discounting is not a compromise between E
and H, but lies even further from E than H had suggested.
3.1.2 Rachlin (Hτ, hτ; τ)
An alternative way to generalize the hyperbolic was proposed by Reference RachlinRachlin (2006), and also presented in Reference Mazur, Commons, Mazur, Nevin and RachlinMazur (1987):
Here, the exponent τ applies specifically to T rather than the whole brackets. This minor modification leads to a subtly different model. Rearranging (19) to isolate the rate parameter, we get:
In this version of the hyperboloid, the numerator (the treatment of money) is the same as for the hyperbolic. However, unlike in the previous four models, time may be treated subjectively by means of a Stevens-like power law. Similar to before, if τ =1 we have the hyperbolic. But once again, τ < 1 in empirical data. Thus, subjective time is increasingly compressed at longer periods. The typical range for τ is [.67, .90] (Reference McKerchar, Green, Myerson, Pickford, Hill and StoutMcKerchar et al. 2009, Reference McKerchar, Green and MyersonMcKerchar et al. 2010) which is just slightly lower than other estimates of the subjective time exponent (Reference EislerEisler, 1976). This is the first model we have considered in which the rate parameter cannot be expressed in straightforward units of measurement.
3.1.3 m, τ, or m relative to τ?
Comparing models the money and time parameters from Hm and Hτ, in 3.1.1 and 3.1.2 we cited typical (m, τ ) exponents as being, very approximately (1.5, 1) when Hm was the model, and (1, .7) when Hτ was the model. The utility of money is generally conceded to be m < 1. This may lead us to believe one of two things. Either the estimates of m and τ are discrepant with each other, and in the case of m, highly discrepant with past research. Alternatively, that what may count behaviorally, over and above the absolute values of m and τ, is their sizes relative to each other. Suppose it is a psychological fact that m > τ, i.e. that subjective money is less concave (more convex) than subjective time, then in fitting m and τ relative to each other, both models are consistent. But if one model constrains τ = 1 (as Hm does), then the behavioral requirement that m > τ will force m to be greater than 1. Likewise if the other model constrains m = 1 (as Hτ does), the behavioral requirement m > τ will force τ to be less than 1. This is what we find.
The requirement m > τ is consistent with Reference Zauberman, Kim, Malkoc and BettmanZauberman, Kim, Malkoc and Bettman’s (2009) conclusion that perception of time are more labile than perception of money, but it is not consistent with exponential discounting for which m ≪ τ.
3.2 Present bias / present premium models
3.2.1 Quasi-hyperbolic (β-δ) discounting (qH, q; β)
Quasi-hyperbolic discounting (qH) is rarely used in psychological research, though it is used extensively by economists hoping to preserve as much of the exponential model as possible. In the discrete time version of the exponential model each factor discounts the previous one by δ (= 1/(1+r)) to form a geometric progression of discount factors: {1, δ, δ2, δ3,…δn} for t = 0, 1, 2, 3…n, respectively, with δ < 1. As explained in Section 2.1, when the compounding periods become very small, and n becomes correspondingly large, we have continuous compounding, and therefore E itself. Contrasting with discrete-time E, the quasi-hyperbolic model posits discount factors: {1, βδ, βδ2, βδ3, …βδn} for t = 0, 1, 2, 3…n, respectively, with 0 < β, δ < 1 (Reference LaibsonLaibson, 1997). If β = 1 we would have a straightforward compounding model, as described in equation (9). But if instead, β < 1, this parameter acts to give a one-off boost to discounting over the first compounding period. The purpose of β is to help tick the box of unexpectedly steep discounting at short durations, which is the hallmark of actual behavioral data, and which first motivated the use of hyperbolic discounting. Thereafter, the model assumes that discounting follows the standard normative model. Paralleling the development in Section 2.1, the quasi-hyperbolic can also be used for continuous discounting (e.g., Reference Benhabib, Bisin and SchotterBenhabib, Bisin, & Schotter, 2010). The discount factor D is:
The rate parameter for quasi-hyperbolic discounting is therefore:
All F first get scaled by the additional parameter β before being treated by the exponential model. Obviously, if β = 1, then q = r as in equation (12). It is thus clear that qH discounting is hyperbolic only in its intent to mimic the steep initial discounting of the hyperbolic model, but in every other sense it is an exponential model.
The qH model may have been motivated pragmatically to preserve exponential discounting and all the useful mathematics that goes with it, while also modeling initial steep discounting. Nonetheless, the idea that F (but not P) gets a special “tax” simply because it is not received right now does have a more constructive justification. There is a qualitative difference between now and any time to come, which we all appreciate intuitively, and which language mirrors in verb tenses. From this perspective, the discontinuity in qH between t = 0 and t > 0 is not an ugly kludge to workaround bothersome behavioral evidence, but a clever modeling device that allows what happens now (P) to be treated differently from all future events (F). In this way qH, a model devised by economists for economists, has the capacity to capture a psychological distinction that the other models cannot.
To help rescue this insight from the limitation of being identified exclusively with the exponential model, let γ = 1 / β . Whereas β captures the idea that F is less than it should be, γ captures the idea that P is more than it should be, and we call γ the present premium. Analogous ideas are met in risky decision, where a certain reward (p = 1) are valued at a premium over rewards with p < 1; and also in the premium due to mere possession or the endowment effect (Reference McKerchar, Green and MyersonThaler, 1980; Reference Sen and JohnsonSen & Johnson, 1997). Rewards that are certain, mine, and now are all over-valued. Potentially, the models we have considered or are about to consider, could incorporate a present-premium parameter by simply replacing P with γ P (or F with β F) in all calculations. Reference Benhabib, Bisin and SchotterBenhabib, Bisin and Schotter (2004) formulate exactly such a hybrid between H m and qH in this way (see also Section 4.4, and Reference Tanaka, Camerer and NguyenTanaka, Camerer & Nguyen, 2010).
Nonetheless, there are still issues to be confronted with qH. In particular, if β < P/F in a particular choice, the model predicts P should always be preferred to F, no matter how short the delay in F—unless someone’s internal rate parameter is negative. Reference LaibsonLaibson (2003) suggested “calibrating” qH with β ≃ .5, meaning that 21 of Reference Kirby, Petry and BickelKirby, Petry, and Bickel’s (1999) 27 choice questions would be in the negative rate parameter category. Even β = .90 would put 8 questions into that category. Summarizing several empirical studies in economics, Reference Van de Ven and Wealevan de Ven and Weale (2010) noted β s of .296, .308, .674, .687, .846, .942; and .825 in their own work; and in Reference Albrecht, Volz, Sutter, Laibson and von CramonAlbrecht, Volz, Sutter, Laibson and von Cramon (2011) the median β from individual experimental data was .86, with 24 of 27 participants having β < 1. If these estimates are close to what individuals use in binary choice, then β < P/F would occur more than just occasionally in typical data.
The quasi-hyperbolic is popular with behavioral economists. It lends itself to convenient testing against the normative model E, by testing whether β is significantly different from (less than) 1. Unfortunately, in the literature qH has rarely been tested against the kinds of models surveyed here which are more potent challengers in that they themselves have consistently proven better than E. Furthermore, Reference Kable and GlimcherKable and Glimcher (2010) argued that the present bias is more strictly a soon-as-possible bias, implying that a deflationary β should be applied to all f (t > 0), and not just P (t = 0). Finally, as has already been pointed out in Section 1.3.3, nothing ever actually happens at t = 0, in that a reward offered “now” is actually received at t > 0. Therefore, the special status of t = 0 in qH can be questioned on the grounds that it may never occur in practice.
3.2.2 Benhabib et al.’s fixed cost model (X, x; χ)
As an alternative to the percentage decrement for non-present rewards, Reference Benhabib, Bisin and SchotterBenhabib, Bisin and Schottter (2010) suggested using a fixed cost to model present bias—that is, an absolute decrement: use (F – χ ) in place of F. Thereafter use the exponential model, exactly as in qH.
They found a present bias / present premium of about $4 among amounts of $10 through $100. The fixed cost model better fitted their data than the qH model. A different, though very similar model is obtained if χ is added to P rather than subtracted from F (see Section 4.4). Reference Hardisty, Appelt and WeberHardisty, Appelt, and Weber (2012) found that χ was positive for both gains and losses, suggesting a general “want-it-now” bias.
3.3 Read’s interval model (B, b; θ)
Reference ReadRead (2001) presented his model in terms of a discount fraction D that occurs within the time window [t, T]. D is the fraction by which F is reduced by being at the end of the interval (T), rather than the start (t): namely, f / F. The exponent θ applies to the time interval, rather than time itself (as would be the case with the exponent τ, which is not used here). The algebraic steps to isolate the rate parameter b are:
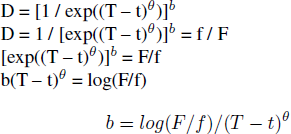
From equation (24) we see that Read’s is an exponential model performed on the subjectively (because θ ≠ 1) perceived time interval (T – t). It nests the standard exponential model E when the interval of inspection starts from t=0 (at which point f is to be known as P), and when subjective time is assumed to be linear with objective time (θ = 1).
While this model seeks to understand cognitive processes through the use of interval data (t > 0), it still must compete with other models at the particular case of t = 0, even if a given competitor model has not (yet) been generalized to the case of t > 0.
3.4 Roelofsma—exponential time (V, v; υ)
Arguing from the Weber-Fechner Law of logarithmic sensitivity to psychophysical stimuli, Roelofsma (1996) presented his model as:
If we take U(F), the utility of F, as itself being logarithmic as in the exponential model E, and move from discrete to continuous time, we derive the rate parameter:
Whether log(υ) is an intrinsic part of this model is not really discussed by the author. If it is not, the obvious choice is to set υ = 1, so that this model becomes a simple rate parameter model in log money and log time, with no additional parameters to be estimated. In treating both money and time logarithmically, among the models I have surveyed, Roelofsma’s is the most enthusiastic adherent of the Weber-Fechner law. Assuming υ = 1, and writing (26) as: v = [log(F) – log(P) ] / log(T), we see that Roelofsma is structurally similar to the arithmetic model except that, instead of using raw values of F, P, and T in the rate parameter equation, each is replaced with its logged equivalent.
3.5 Synopsis of the models so far
E is the normatively correct model to value investments. It assumes a continuously compounding interest model of growth. But E fails to capture important aspects of how laypeople actually evaluate intertemporal choices. qH extends E by making a distinction between present choices and future choices. In qH, all choices in the future are devalued by a constant scalar β before treating them as in E, which itself is the special case of qH when β = 1. Model X, like qH, maintains that there is a special difference between P and all future values F, but whereas qH treats the present premium multiplicatively, X does so additively.
For over two decades, H has been the psychologists’ default alternative to E in that it consistently estimates people’s actual discounting behaviors better than E. H is equivalent to a simple interest model of growth. The hyperboloid models are extensions of H that treat money (Hm) and time (Hτ) as non-linear. Hm is equivalent to H when its additional parameter m = 1, and E when 1/m → 0. But past evidence estimates m to be less than 1, which might imply increasing utility to money, contrary to classical theory and common intuition. Also, Hτ is equivalent to H when its additional parameter τ = 1. The mental operations involved in A are simpler than those in all other models, which all start by forming a ratio between (possibly transformed) F and P. Model A starts by forming a difference between F and P.
The special case of t = 0 in Read’s model B (all time intervals start from now; hence f = P) presents as a hybrid between E and Hτ. It is an exponential model (logarithmic money) calculated on subjective (power law) time. Of course, in modeling time intervals in general, not just ones that start from the present, Read’s model aims to examine phenomena that the others cannot. Roelefsma’s model V treats both money and time logarithmically, which makes it equivalent to A, where all monies and times have first been logged.
Finally, because of the reciprocal T in calculations of r, h, d, hm, q, and x for a given P and F, all of these rate parameters decline hyperbolically with time. In fact, one might distinguish models E, H, A, Hm, qH, and X from each other only by their treatment of money, and once that is determined in the numerators of their respective rate parameter equations, r, h, d, hm, q, and x all decline identically with objective time. This neglected perspective suggests the essential difference between the five models of intertemporal choice, A, Az, H, E, Hτ, qH, and X has nothing to do with time per se, and could even be tested against each other by considering a single fixed time gap between P and F.
3.6 Time (im)patience models
From the point of view of modeling rate parameters, most of the above models have focused on their treatment of money, making few inroads into modeling the subjectivity of time. In this Section we collect together research that takes a serious look at how time is perceived—while incidentally accepting the log(F/P) of model E as a given.
3.6.1 Ebert & Prelec’s constant sensitivity (CS) function (C, a; b)
“Given that unit elasticity defines compounding discounting [E], it is natural to interpret lower-than-unit elasticities as indicating insufficient time-sensitivity relative to compound discounting. If elasticity is constant and equal to b > 0, the discount function has the constant-sensitivity form” (Reference Ebert and PrelecEbert & Prelec, 2007, p.1425), which is:
As b → 0 we have diminishing time sensitivity. If b ≫ 1, then the CS function begins to appear as a step function, meaning that time is ever more clearly dichotomized into “near future” and “far future” (at the boundary 1/α ). See their Figure 1. We can isolate the rate parameter associated with the CS model from equation (27) as:
Clearly, when b = 1 (unit elasticity), we have model E as the special case. Ebert and Prelec note, but avoid, the similar discount function:
leading to the rate parameter:
which is a special case of the generalized hyperboloid to be examined in Section 4.3, with m → 0.
3.6.2 Bleichrodt et al. Constant Relative Decreasing Impatience (CRDI) functions (M, ρ; ψ, (β =1))
CRDI is explicitly described as an analog of constant absolute risk averse functions (CARA) that appear in risky choice models. Reference Bleichrodt, Rohde and WakkerBleichrodt, Rhode, and Wakker (2009) observed that hyperbolic discount functions were developed to account for decreasing impatience. That is, relative to exponential discounting, people consistently show greater impatience (for P) in the short term, but greater patience in the longer term. They also noted that such models failed to accommodate “increasing impatience or strongly decreasing impatience” (p. 27), particularly given the attempt to model individuals’ discounting behavior: hence their search for discounting functions to fulfill this need. Let D(T) be the discount function (i.e., D(T) = P/F). Then their CRDI function is / are:
-
(i) D(T) =

-
(ii) D(T) =

-
(iii) D(T) =

Examining each in turn, we have for ψ > 0,
![]() , thus:
, thus:
The following points should be noted. First, money is treated as in qH, with β fulfilling the same role in both models. Second, there is a power law on time; if β = 1, the model is exactly the route not taken by Reference Ebert and PrelecEbert and Prelec (2007), as in equation (30). Third, if ψ = 1, we have objective clock time, and thus “constant impatience”; if 0 <ψ < 1, we have the conventional view that time becomes increasingly contracted the more distant in the future it is, and thus we have “decreasing impatience”; but if ψ > 1, the more distant the time, the more stretched it becomes, which therefore models “increasing impatience”.
Examining ψ = 0, we have:
If β = 1, we have Roelofsma’s model (presuming υ =1), described in Section 3.4.
Finally, if ψ < 0, we have:
In this case the denominator asymptotes to zero, but from below. It is designed to model impatience that decreases more rapidly than for the first part with 0 < ψ < 1. In order for ρ to be positive (Bleichrot et al, 2009, Definition 4.1, p. 31), we must have that β < P/F so that the log in the numerator is negative allowing the minus signs to cancel.
As ψ moves through zero from above, for a given T > 0, the denominators in parts (31), (32) and (33) become 1, logT and –1, respectively. This means that any algorithm that hopes to recover the impatience parameter ψ from data has a discontinuity to negotiate at ψ = 0. It may therefore be better to think of (i), (ii) and (iii), or equations (31), (32) and (33), as three distinct sub-models, rather than a single model.
3.6.3 Bleichrodt et al. Constant Absolute Decreasing Impatience (CADI) functions (N, σ; η, (β = 1))
Their analog of a CARA Constant Relative Risk Averse function is the CADI function given by:

“[β] is a scaling factor without empirical meaning in the sense that it does not affect preferences”; “[η ] is the constant that indicates the convexity of log(D)”; and the rate parameter σ “determines the degree of discounting.”
Looking first at the η > 0 part:
The denominator ![]() is a convex function,
indicating increasing impatience. It is the analogous equation to the first
part of 3.6.2, in the region ψ > 1.
is a convex function,
indicating increasing impatience. It is the analogous equation to the first
part of 3.6.2, in the region ψ > 1.
For η = 0, we have:
which is the Exponential model, and for η < 0 we have:
![]() is a decaying function with time if η < 0, but because of
the negative sign, the denominator becomes a concave increasing term, and is
therefore analogous with 3.6.2,
part(iii) and equation (33).
is a decaying function with time if η < 0, but because of
the negative sign, the denominator becomes a concave increasing term, and is
therefore analogous with 3.6.2,
part(iii) and equation (33).
The same kind of remarks made for the CRDI functions, concerning algorithms and betas can be repeated here.
3.7 Size-sensitivity in the arithmetic model (A z, d z; z)
Returning to the arithmetic model, one shortcoming is its insensitivity to size. That is, if someone prefers to receive $11 in 2 days rather than $1 today, model A assumes that person would also prefer $1,000,011 in 2 days to $1,000,001 today. Both imply d = 5 so that if d exceeds the internal d0 in the first scenario, implying that F should be preferred to P, d will also exceed d0 in the second. However, in the second scenario, just contemplating the impact of becoming a millionaire right now is likely to affect the internal criterion d0 in the sense of requiring greater “wages for waiting.” A more flexible model is therefore to suggest that the rate parameter may vary with the size of P. For instance, d may be given by a power law scaling of a rate parameter dz which is stable and does not vary depending on the size of the choices offered,. Hence, d = Pzdz. Therefore, we have:
If z = 0, dz is not size-sensitive at all, and we have model A. If z = 1, dz is highly size-sensitive and in fact we have the simple hyperbolic model H. Thus the size parameter z links A with H.
An alternative is to scale d by F−z (Reference KirbyKirby, 1997), though see Section 5.1 for arguments why P is preferred to F.
4 Rate parameter + 2 models
4.1 Killeen’s additive utility model (K, k; m, τ)
Reference KilleenKilleen (2009) started from the
assumption that the marginal change in utility with respect to time follows a
power law; also, that utility and value are themselves related by a power law.
Taken together these were shown to yield an equation of the form:
![]() (Reference KilleenKilleen, 2009, equation 6, p. 605), where his vt, v,
α, β, t, and λ are respectively our P, F, m,
τ, T,and k. He explained as follows: “this additive utility
discount function is the central contribution of this article. It is additive
because the (negative) utility of a delay is added to the nominal utility of the
deferred good.” (p. 605). Some rearrangement isolates the rate parameter
to give our canonical form:
(Reference KilleenKilleen, 2009, equation 6, p. 605), where his vt, v,
α, β, t, and λ are respectively our P, F, m,
τ, T,and k. He explained as follows: “this additive utility
discount function is the central contribution of this article. It is additive
because the (negative) utility of a delay is added to the nominal utility of the
deferred good.” (p. 605). Some rearrangement isolates the rate parameter
to give our canonical form:
Clearly, when both m = 1 and τ = 1, we have the simple arithmetic model. The numerator can be written as:
So that as m → 0, it becomes:
m.log(F) – m.log(P) = m.log(F/P)
But since m is a common factor, it can be treated as a scaling constant, meaning that K nests E when m → 0 and τ = 1. It also nests the particular t = 0 case of Read’s model, which occurs in K when m → 0 and τ is a free parameter. Killeen’s used his model to survey aggregated data from past research, finding that m ≃ .15, and τ ≃ .53. Both parameters are smaller than other researchers have estimated, and in particular m < τ , which is contrary to evidence collected by researchers in connection with Hm and Hτ. Note, however, that within the datasets that Killeen examined, the number of observations used to fit the model was never greater than eight, which is rather small for non-linear estimation.
4.2 Killeen, intervals, and started time (Kτ, kτ; m, τ)
Killeen’s additive utility model can be generalized to time intervals that start in the future (at time t ≠ 0), either with a power law on the interval, as modeled in Reference ReadRead (2001) and Section 3.3:
or with a power on each point in time itself:
There is an important distinction between these models for time exponents θ or τ if they are ≪ 1, which exaggeratedly condense distant time. In our first generalization of Killeen, as θ → 0, the denominator (T − t)θ → 1, which means that people would be completely time-insensitive, and therefore presumably always choose F over f. However, in the second generalization, as τ → 0, the denominator (Tτ – tτ) → τ .log(T/t), meaning that at this extreme people become only logarithmically (in)sensitive to time. Started time does not affect (39) since the start is added to both T and t, which cancel out.
Because of the symmetry in the treatment of money and time in the kτ generalizationFootnote 3, and to allow the possibility that subjective time is logarithmic, as argued in recent research (Zaubermann et al, 2009), we now focus attention on kτ. But immediately we hit a problem, which is that if t = 0 (as it usually is in intertemporal choice questionnaires), equation (39) cannot be distinguished from (40), so that we end up with the same time insensitivity as in kθ when τ → 0. Persisting with the logarithmic limit idea doesn’t help either because of divide-by-zero problems.
As argued earlier, because of log(0) problems a useful generalization of Killeen is to use started timeFootnote 4:
where T* = T + ε, and t* = t + ε , and ε is small. This form is flexible enough to capture many possible states of the world, as reflected in the recovered exponents m and τ . If m → 0, subjective money (F, f) would be logarithmic. If τ → 0 started time (T*, t*) would be logarithmic. If m and τ were close to 1, money and (started) time would be linear (objective), while intermediate values of m and τ would indicate that subjective time and money have less-than-logarithmic curvature. It is also possible that both m and / or τ could be > 1.
4.3 Dual hyperboloid with subjective money and time (Hmτ, hmτ; m, τ)
As a robustness analysis, Reference Doyle and ChenDoyle and Chen (2012) used power exponents to model time and money for A, which then becomes model K, and for the hyperbolic, which then becomes:
This nests a number of models already considered. The rate parameter hm for Green and Myerson’s hyperboloid model is the special case when τ = 1. The rate parameter hτ for Rachlin’s hyperboloid occurs when m = 1; and the hyperbolic rate parameter h occurs when both m = 1 and τ = 1. Furthermore, when m → 0 we have:
Which is model B (Read), and b = h m
τ. Note also that the subjective-time exponential only has one
additional parameter, because any attempt to introduce a new exponent for money
results in ![]() , so that m just becomes a
scaling constant. The model Reference Ebert and PrelecEbert and Prelec
(2007) reject, equation (30), occurs when m → 0.
, so that m just becomes a
scaling constant. The model Reference Ebert and PrelecEbert and Prelec
(2007) reject, equation (30), occurs when m → 0.
In conclusion, most of the models considered so far can be generated from equation (42) as special cases. However, the CS model that Elbert and Prelec do propose, equation (28), has the exponent acting on all of log(F/P), not just what is in the brackets. Therefore, CS cannot be derived.
Similarly, the general hyperbola (Reference HarveyHarvey,
1986) cannot be derived as a special case of equation (42). It has the form
![]() . As Reference Loewenstein and PrelecLoewenstein and Prelec (1992) state: “The α
-coefficient determines how much the function departs from constant discounting;
the limiting case, as α goes to zero, is the exponential discount
function, e−βT.” When
β=α , it is the simple hyperbolic, which we can
write as P = F / (1 + βT), as in Section 2.2. Therefore β may
be treated as a rate parameter for the special case of both hyperbolic and
exponential, and in the more general case,
. As Reference Loewenstein and PrelecLoewenstein and Prelec (1992) state: “The α
-coefficient determines how much the function departs from constant discounting;
the limiting case, as α goes to zero, is the exponential discount
function, e−βT.” When
β=α , it is the simple hyperbolic, which we can
write as P = F / (1 + βT), as in Section 2.2. Therefore β may
be treated as a rate parameter for the special case of both hyperbolic and
exponential, and in the more general case, ![]() . Finally, as α becomes
large, the discounting function becomes increasingly step-like.
. Finally, as α becomes
large, the discounting function becomes increasingly step-like.
4.4 Benhabib et al.’s generalization of E, H, qH, and X (G, g; β, χ)
Reference Benhabib, Bisin and SchotterBenhabib, Bisin and Schotter (2004) presented their model as a discount function:
Substituting D = P/F and re-arranging, we have:
When n → 0, we have:
Thus:
which is E if the quasi-hyperbolic multiplier β = 1, and the analogous additive term χ = 0. If β = 1, and χ = 0, and n = –1, we have H, the simple hyperbolic.
We begin to see here how elements of different models may be combined to good effect. In this example the authors were able to test whether the multiplier β or additive element χ was more predictive of behavior. In their analyses, it was the latter. They also noted that their particular data had little power to distinguish between functional forms H (n = -1) and E (n = 0), though the main point to note here is that their generalization model does allow for testing this possibility.
4.5 Hyperboloid over intervals (Hmω, hmω; m, ω)
Reference Green, Myerson and MacauxGreen, Myerson and Macaux (2005) extended Green and Myerson’s model described in Section 3.1.1 to include time intervals that do not begin at t=0. Starting from their statement of the model in their equation A16, we derive the following equation for the rate parameter hmw. Letting M = (F/f)m – 1 be the numerator, exactly as in Section 3.1.1, then:
Clearly, when t = 0, this model reduces to Hm. But when t > 0, the authors identified different models according to the values of ω and m.
Equation (46)a: ω = 0 is their elimination by aspects model. One aspect that is common to the two choices (f, t) and (F, T) is the wait to the first choice, and so it is eliminated, reducing the time component to (T – t). We should also note that f is common to the monetary choices, but this aspect is left untouched in 37a.
Equation (46)b: m = ω = 1 is their present value comparison model. In this model, people are assumed to discount both F and f to present values, using the simple hyperbolic model in Section 2.2 (i.e., m = 1).
Equation (46)c: m = 1 is their common aspect attenuation model. Once again, F and f are assumed to be hyperbolically discounted to a present value, but this model assumes that an extra attenuation factor, operationalized by the weight ω , may act on f.
One point to note from the general statement in (46) is that although a money-only component can be identified in the numerator, the subjective time component in the denominator is not independent of money, because the denominator in (46) has the additional term ω tM, and M has terms involving F and f. This contrasts with all other models presented thus far. Finally, equation (46) implies that if (F ≫ f), M could become large enough so that (T – t) < ω tM, thus turning the rate parameter negative.
5 Rate parameter + 3 models
5.1 Size-sensitive J model (J, j; z, m, τ)
If we combine the size-sensitivity component described in 3.7 with the started-time version of Killeen’s model extended in Section 4.2 to cope with discounting over non-present time intervals, we get a general model that generates many of the above as special cases:
First, we use the triplet (z, m, τ), each taking values of 0 or 1 to describe whether money and time are modeled as linear (m = 1, τ = 1) or logarithmic (m → 0, τ → 0); and whether there is size-sensitivity (if z = 0 there is not). J nests the following simpler models: Exponential is (0,0,1); Hyperbolic is (1,1,1); Arithmetic is (0,1,1); Roelofsma, if υ is take to be 1, is (0, 0, 0). Moreover, other models can be stated as partially constrained versions of J: Green and Myerson is (m, m, 1), i.e. z = m; Rachlin is (1, 1, τ ); Read with t = 0 and t* = 1 is (0, 0, τ ); Size-sensitive Arithmetic is (z, 1, 1); the general hyperboloid Hmτ in 4.3 is (m, m, τ ); and Killeen is (0, m, τ ). Also nested in J are several of the memory trace models described in Reference Yi, Landes and BickelYi, Landes, and Bickel (2009), namely “power” (0, 0, 0)—see also Roelofsma; “exponential power” (0, 0, .5), and “hyperbolic power” (1, 1, .5).
In being able to generate these alternative models, J has a number of useful properties. First, there is the simple matter of parsimony. We need hold in mind a single equation from which many others may be generated. Second, the generation process encourages us to consider and investigate other models that could be generated from the triplets, but have not. For instance, there are eight possible fully-constrained, simple rate parameter models. Each is a combination of the 0 or 1 for each of the triplet values z, m, and τ . Only four of these models have been considered: what of the other four? Similarly, though less mechanically, new models may be considered with partial constraints. Last, but not least, one may use model J with no constraints to recover parameters for z, m, and τ . The fact that so many models may be generated from this form hints that the best fitting model may be a compromise between of all of them, as should be evident if the parameters z, m, and τ were all to fall between 0 and 1.
This model scales by P−z rather than F−z because the latter is less productive in generating other models as special cases, and also because it is more likely that P, will be used as the given situation, against which F will be compared, rather than vice versa. After all, P is mentioned first in the typical question frame (e.g. “Would you prefer to receive $70 now, or $100 in 20 days?”), and is on offer right now. Thus F will be evaluated in terms of P. Nonetheless, it may be possible to prime F to fulfill the role of given information, as in the question frame: “Assuming you can receive $100 in 20 days’ time, would you accept $70 now instead?” Thus biasing P to be evaluated in terms of F. Manipulating the salience of P relative F, or vice versa, can be taken a stage further in matching tasks where people estimate their indifference points between P and F. Thus if people are required to adjust P for a fixed F they will be biased towards scaling by F−z; whereas if they adjust F for a given P, they will be biased towards scaling by P−z. Using F−z gives rise to a parallel set of models to those presented here. But the degree to which P−z outperforms F−z as a scaling component, or vice versa, and their susceptibility to manipulation are all matters for future empirical investigation.
5.2 Discounting by intervals, DBI (I, I; m, τ, θ)
Like Read’s model, Reference Scholten and ReadScholten and Read’s (2006) discounting by intervals (DBI) model is designed to highlight phenomena which occur over several intervals that do not necessarily include the special one bounded at t=0. Nonetheless, as a viable model it must be able to stand comparison with other models when t=0. The rate parameter for DBI is:
This model extends Read’s in two ways. First, money is modeled as in Green and Myerson with a to-be-estimated exponent m, rather than with log(F/f), as in Read. This is more flexible because the power form nests the logarithmic money form. Second, although there is still an exponent on the time interval, the times in the interval are themselves subjective. Therefore, Read’s model is nested in DBI as the special case where m → 0, and τ = 1. Note that if t = 0, the denominator becomes Tτθ. Given that τ θ only occur together, they can be treated as a single parameter, and DBI becomes the generalized hyperboloid Hmτ. Also, if θ = 1, we approximate J (m, m, τ ) if τ is sufficiently far from 0 so that started and objective time are effectively equivalent.
Finally, the nesting of time and time-interval exponents in the denominator (Tτ – tτ)θ means that care must be taken in experimentally estimating the separate parameters.
6 Discounting models with no closed-form rate parameter
6.1 Two rate parameters—two exponentials discounting (Eβδ, rβ, rδ; w)
This model is related to the quasi-hyperbolic model in its intent to separate short-term from long-term processes. But, whereas qH separates events at t=0 into a qualitatively distinct category from those at t>0, this model deals with the same short/long-term issue in a more graded manner. Carrying over the same terminology as used in qH, Reference McClure, Laibson, Loewensein and CohenMcClure, Laibson, Loewenstein, and Cohen (2007) suggested a β -system associated with limbic areas of the brain, that is impulsive, myopic, and discounts at a high rate; and a δ -system, associated with prefrontal and parietal cortical regions (“higher man”), which discounts at lower rates. Each of these sub-systems is assumed to discount according to the exponential model, with the overall discount rate being a weighted sum of each sub-system:
where if the first term represents the β-system, then rβ > rδ. Quite explicitly, there are two rate parameters.
6.2 Scholten and Read’s intertemporal tradeoff model—7 parameters (Y, γ, τ, εm, ετ, and three of {a1, a2, b1, b2})
Reference Scholten and ReadScholten and Read (2010) provide a densely argued justification for a complex model which they present in terms of an indifference point between the perk of additional compensation, and the irk of waiting for it. They define the money value function on a future payment F to be:
and a time-weighting function to be:
They define an “effective compensation” to be:
and an “effective interval” between t and T to be:
The point of indifference is when:
such that if ![]() then the irk of waiting is
greater than the perk of compensation, so DM chooses f at t, rather than F at T,
and vice versa if
then the irk of waiting is
greater than the perk of compensation, so DM chooses f at t, rather than F at T,
and vice versa if ![]()
![]() However, Qτ and Qm are not simple
scaling factors, but two-part linear functions:
However, Qτ and Qm are not simple
scaling factors, but two-part linear functions:

ετ is a threshold below which effective time intervals (here just x) are weighted more steeply than above-threshold. Note the similarity of intent with the two exponentials model. Similarly,
If the indifference equation is written out in full, it is possible to see that a discount function of the form f/F cannot be extracted: nor does limiting analysis to t=0 overcome the problem. Similarly, no simple rate parameter emerges from this model. It follows that the indifference equation is the only simple way to present the model. The model requires three parameters to specify the two-part linear function for time (a1, a2, ε τ), three more to specify the equivalent parameters for money (b1, b2, ε m), as well as τ and γ to specify the time-weighting and value functions, respectively. However, the authors note that “if only the relative magnitude of scaled effective differences is of interest, one of these scaling constants {a1, a2, b1, b2} can be set to unity.” (p. 934). This model therefore requires seven parameters to be estimated. So clearly, one of the biggest problems in testing this model is the number of parameters to be recovered, which means designing choice problems over which the parameters are sufficiently independent of each other, and the number of observations sufficiently large in order to estimate the parameters adequately.
The tradeoff model treats time and money symmetrically, which we argued in 1.3.4 should be the default position for a quasi-psychophysical theory of time and money. Indeed, the authors explicitly deny that people are discounting in any way that an accountant would recognize, espousing instead a thoroughly psychological perspective on intertemporal choice.
7 Model families and newborns
7.1 Models have similar forms
The world is simpler than a list of twenty or so models might suggest. Our presentation of models via their rate parameters emphasizes the following common structure:
where s(.) and S(.) are functions that return subjective perceptions of the money and time aspects, respectively, and ⊗ is an operation by which these become combined. According to this view, if someone operates according to the exponential model it is because his/her subjective perception of money is logarithmic, while his/her subjective perception of time is linear. In (57), subjective perceptions then get combined by the operation ⊗. In most cases, ⊗ is arithmetic division, but can be subtraction, or conceivably something else. The separability of s and S in the mathematics implies that subjective perceptions of time and money should take place independently of each other. In most models, objective time and money are transformed into subjective equivalents by power laws, or logs, but other transformations are possible.
To further simplify the map of the models surveyed here, note that half are special cases of model J, and the present-bias models of qH and X could also easily be incorporated into J. Two further themes that lie outside J are: the time impatience models of Section 3.6 that go to town on the modeling of time itself; and models that place power laws on time intervals rather than on points of time—Sections 3.3 and 5.2. Finally, we are left with just four models that are not captured by these themes. First there is the two-exponentials model—which is just a doubling up of the reference model E, as if we had two normative discounters in the same head: one patient (δ ), the other impatient (β ). Then there is Reference Scholten and ReadSchotten and Read’s (2010) trade-off model I, which for all its complexity is still recognisable as an assemblage of parameter-based treatments of subjective money, time, and intervals. Hmω, although an innocuous extension of the hyperboloid to time intervals turns out to be the one model for which time and money cannot be cleanly separated.
7.2 Speculative models
We end with a sample of speculative models (newborns) that have clearly been assembled from the components of existing models. Being able to mix and match almost indefinitely emphasizes the family resemblances that exist between models, and helps to compare and contrast treatments of time and money. Some of these examples are semi-serious; others are intended to provoke thought.
7.2.1 Arithmetic interval model
One of the innovations in B and I is that intervals and subjective intervals are treated as if psychophysical elements in their own right, which may then be investigated using power laws, and so on. We cross this with Killeen (extended) to give the hybrid:
For mnemonic value note that µ is “mu” Greek m; and θ “theta” sounds vaguely like T.
7.2.2 Fully additive model
Instead of treating ⊗ as a division in 7.2.1, we could treat it as a subtraction, echoing the difference models examined in Stevenson (1986):
The weighting coefficient w cannot simply be interpreted as the perceived relative importance of time, because it also rescales for m, µ, τ, θ, and units of time and money. However, Stevenson found little support for this way of combining time and money, compared with multiplicative (ratio) forms.
7.2.3 Fully multiplicative hyperbolic model
Analogously, if H treats money as a percentage increase (that gets averaged over time), then a model that also treated time as a percentage increase would look like:
This example highlights the point that the default setting in models is to treat time as additive, whereas money is treated as multiplicative. From the point of view of Reference StevensStevens’ (1946) levels of measurement, both are ratio scale measurement, with properly defined zeros. So if in theory we can treat time and money symmetrically, what is to stop the naïve behavioral theorist thinking likewise?
7.2.4 Time-size and money-size sensitive model
Model J only treated money as size-sensitive. A symmetrical treatment of time and money is instead:
where g is the time analog of z for money, implying that someone’s criterion rate parameter may vary, not just with the size of f, but also how far in the future f is offered.
7.2.5 Arithmetic present premium model
A present premium can be incorporated into other models. Using both the multiplicative and additive components of Reference Benhabib, Bisin and SchotterBenhabib et al’s (2004) generalizing model in Section 4.4, the arithmetic model would become, for instance:
8 Conclusions
This paper has surveyed delay discounting models that have appeared in several literatures. Our presentation emphasizes that models have a clearly separable time component, a separable money component, and a method of combining these components into a rate parameter / decision parameter. Within the components that transform objective monies and times and intervals into subjective equivalents, we have seen that the power law occupies a special place in delay discounting models, particularly given that log laws may be derived as special cases. However, despite the many models presented in this survey, it may turn out that none of them portrays ITC behavior particularly accurately—the door must always be left ajar to improvements. Although researchers have been inventive in their modeling of the time and money components, there has been less interest shown in exploring alternatives to power laws (which have been taken as the basic nuts and bolts of discounting models), or how the time and money components should be combined. Whereas past research has favored power laws over log laws or the negative exponential to represent the utility function, nonetheless even it may be flawed. For instance, Reference KirbyKirby (2011) has shown that power laws depart significantly from utility, as incidentally do the other standard forms considered. Kirby’s findings have yet to be extended from utility in risky choice to utility in intertemporal choice. Even more radically, the Decision-by-Sampling model (Reference StewartStewart, 2009) foregoes the parameterisation of utility and time in favor of a memory-based approach. Another possible direction for future research in individual decision making is to more explicitly model the “fuzzy math” (Reference Stango and ZinmanStango & Zinman, 2009) of the typical insufficiently competent mathematician who is required to think about financial and other numerically presented choices. But given the large numbers of models and variants that have appeared in the literature, the re-usability of components, and the ease with which speculative models can be assembled from them, a chief problem for future research is to heed Occam’s razor by limiting the number of parameters a model employs to only those that are strictly necessary. Finally, by gathering these models into one place and thereby shining a light on them, it is hoped that future research will be more proactive in testing models against each other, and in manipulating choice behavior through selectively manipulating the parameters that are supposed to drive those behaviors.



