1 Introduction
Participants asked to determine the degree of contingency between their press of a button and the onset of a light increase their ratings with light onset frequency even when the light is objectively uncontrollable (Reference Alloy and AbramsonAlloy & Abramson, 1979; Reference Jenkins and WardJenkins & Ward, 1965). People place greater value on lottery tickets they have personally chosen than on tickets that have been handed out (Reference Langer and RothLanger, 1975; Reference Wohl and EnzleWohl & Enzle, 2002). Slot-machine players choose machines that have not paid out in some time and make use of rituals and lucky charms (Reference HenslinHenslin, 1967; Reference Livingstone, Wooley and BorrellLivingstone, Wooley & Borrell, 2006; Reference Wood and ClaphamWood & Clapham, 2005). All of these phenomena are considered instances of the “illusion of control”, the overestimation of contingency between personal actions (strategies) and task outcomes in games of chance. The illusion is thought to be caused by situational factors (e.g., the availability of a choice between action alternatives) in interaction with held beliefs about these factors. In this sense, the illusion is an inference based on situational information and prior beliefs (Reference CrockerCrocker, 1981; Reference Harris and OsmanHarris & Osman, 2012). The illusion expresses itself in repeated behaviours (e.g., strategic errors, rituals) as well as explicit ratings of control over real-world and laboratory gambling tasks.
In light of the many potential real-world consequences of illusory control inferences, a large number of laboratory studies have addressed their situational determinants (for a review, see Reference Thompson, Armstrong and ThomasThompson, Armstrong & Thomas, 1998). The studies typically involve a laboratory task with objectively random outcomes, and the task tends to be either familiar (e.g, roulette) or novel (e.g., a button-and-light device). A single situational determinant is manipulated and post-session estimates of control or success-frequency serve as the dependent measure. The most frequently investigated situational determinants have been success-frequency (e.g., Reference Alloy and AbramsonAlloy & Abramson, 1979; Reference Thompson, Schlehofer, Carter, Bovin, Wurzman, Tauber and TrifskinThompson et al., 2007) and opportunity for choice and physical involvement (e.g., Reference Ayeroff and AbelsonAyeroff & Abelson, 1976; Reference Ladouceur and SevignyLadouceur & Sevigny, 2005; Reference Langer and RothLanger, 1975). Other identified determinants include need for the outcome (e.g., Reference Biner, Huffman, Curran and LongBiner, Huffman, Curran & Long, 1998; Gino, Sharek & Moore, 2011) and the opportunity for practice (e.g., Reference Benassi, Sweeney and DrevnoBenassi, Sweeney & Drevno, 1979).
This paper aims to resolve conflicting findings regarding another identified situational influence, namely the “success-slope” (also known as “the sequence of outcomes”; Reference Langer and RothLanger & Roth, 1975). This term refers to how successes and failures are positioned relative to each other in a randomly-generated outcome sequence. A sequence with a descending success-slope begins with a string of successes and concludes with a string of failures. In contrast, a sequence with an ascending slope is characterised by a preponderance of successes at the end.
It is not difficult to propose theoretical reasons for why these three conditions might lead to different judgments. For instance, it has been argued that in a “descending” condition, people are motivated to see themselves as effective agents in the task, and so focus heavily on early successes (Reference Langer and RothLanger & Roth, 1975; Reference Thompson, Armstrong and ThomasThompson, Armstrong & Thomas, 1998). On the other hand, it has been suggested that a run of late successes in the “ascending” condition acts to strengthen control inferences by creating the impression of learning (Reference MatuteMatute, 1995). The difficulty, however, lies in the fact that the empirical findings on this effect are mixed.
To date, five experiments have examined ratings of control and success-frequency following the experience of 30 or so outcomes conforming to the “descending”, “ascending”, or “flat” structures. Their findings regarding the direction of the effect were not consistent. Four studies concluded that inferred control is greatest in the “descending” condition (Reference BurgerBurger, 1986; Reference Coventry and NormanCoventry & Norman, 1998; Reference Ladouceur and MayrandLadouceur & Mayrand, 1984; Reference Langer and RothLanger & Roth, 1975), but one study found that inferred control was larger in the “ascending” condition (Reference MatuteMatute, 1995).
When one looks at the literature a little more closely, a number of difficulties present themselves. The first issue is the potential conflation of the illusion of control with memory effects; that is, the conflation of what is inferred with what is remembered. This issue arises when participants are asked to judge the number of successes that they have had, and these judgments are used as a measure of inferred control. To illustrate the problem, we note that the conclusions of Reference Langer and RothLanger and Roth (1975) are based on observing that participants in the “descending” condition provided significantly higher estimates in response to the following three questions: “How many correct predictions did you have on the 30 trials?”, “How many correct predictions do you think you would have had on the next 100 trials?” and “How good do you think you are at predicting outcomes like these?”. None of these questions directly ask about the degree of control people perceive themselves to have. Responses to these questions could be influenced by factors other than one’s beliefs about ability to control the outcome.
A second problem pertains to the issue of what it actually means to measure “inferred control”. Even when inferred control is measured separately from estimated success-frequency, the literature on the success-slope effect tends to treat inferred control as a unitary construct that can be measured using a single question. As an example, Reference BurgerBurger (1986) relied on a single question asking people to rate the “extent to which you believe that your correct answers were the result of you ability to correctly anticipate events”. There is some evidence to suggest that the illusion of control is a more complicated phenomenon. In a review of the illusion-of-control literature, Reference Rothbaum, Weisz and SnyderRothbaum, Weisz and Snyder (1982) distinguished between two different kinds of perceived control, “primary” and “secondary”. Primary control refers to the belief that outcomes can be influenced through personal skill. In contrast, secondary control refers to the belief that external forces (e.g., luck, God) control the outcome, but one can be aligned with these forces. A statement like “I knew how to make my luck work for me” is a good example of a belief in secondary control, insofar as it implies that luck controls the outcome but is favouring the speaker. In the broader cognitive science literature, a similar distinction has been drawn between beliefs about physical entities and superstitious (or religious) beliefs about supernatural entities (e.g., Reference Atran and NorenzayanAtran & Norenzayan, 2004; Reference Wellman and GelmanWellman & Gelman, 1992). The illusion that physical (i.e., skilled) actions are effective in a game of chance would correspond to the illusion of primary control, while a belief in the effectiveness of superstitious or religious rituals would correspond to the illusion of secondary control.
In view of the evidence that primary and secondary control are distinct constructs, it seems sensible to measure inferred primary and secondary control separately. To that end, we will follow a previous study (Reference Ejova, Delfabbro, Navarro, Christensen, Schier and SuttonEjova, Delfabbro & Navarro, 2010) in adopting a factor-analytic approach. That is, we will treat primary and secondary control as latent variables, estimated by analysing a questionnaire that asks people to rate their agreement with a number of statements, such as “I got better with practice”, “My skill in playing the game [helped me win]”, “I’ve always been a lucky kind of person”, and “A certain lucky way of playing just seemed to work for me”. Factor analysis of the responses is expected to reveal clusters of “primary” and “secondary” statements (Reference Ejova, Delfabbro, Navarro, Christensen, Schier and SuttonEjova et al., 2010). The factor scores recovered for individual participants can then be used as the measures of inferred control.
A third issue that we consider is the choice of control conditions. As noted earlier, the success-slope literature uses the “flat” condition as a control for the two conditions that have success-slopes, namely the “descending” condition and the “ascending” condition. Not all studies have used all three conditions. In our study, we include all three, and include an additional “U-shaped” condition, in which there are clusters of wins at the beginning and at the end. If early wins and late wins have distinct effects on perceived control, this condition might be expected to lead to the highest levels of perceived control. Even so, the inclusion of this new condition is more exploratory than hypothesis driven.
In sum, our study aims to test the direction of the success-slope effect in a way that addresses and demonstrates two methodological issues: the difference between inferred control and remembered win frequency, and the two-faceted nature of the illusion of control.
2 Participants
There were 334 participants (171 males), ranging in age from 18 to 80 (M = 25.0, SD = 11.0) and incorporating members of the general community alongside undergraduate psychology students at the University of Adelaide. Recruitment was conducted through a newspaper advertisement, advertisements placed around campus, and through a research participation website accessible to undergraduate psychology students. As is standard in studies of gambling, participation was conditional on being over the age of 18, having gambled at a licensed venue at least once previously, and not being in the process of receiving treatment for gambling-related problems. Psychology students received course credit for participating.
3 Materials, measures and procedure
The experiment was a self-contained 30-minute computerised exercise divided into four stages. These were: (1) a pre-experimental questionnaire, (2) 48 trials of the experimental task, a “soccer-themed gambling task”, (3) the post-experimental questionnaire, and then (4) additional trials of the experimental task, if the participant so desiredFootnote 1. The four different success-slope conditions (the independent variable) corresponded to differences in the sequence of outcomes experienced during the experimental task (stage 2), but in all other respects the conditions were the same. The dependent measures and covariates all derive from the two questionnaires. The description below gives a broad overview of the study: additional details can be found in the Appendices (A and B).
3.1 The pre-experimental questionnaire
To maximise ecological validity, our experimental task resembled a real-world gambling task. To accommodate this, a pre-experimental questionnaire was used to measure participants’ beliefs about gambling. The obtained scores were, in turn, used as covariates in analyses of the relationship between success-slope and inferred control and between success-slope and remembered success-frequency. Similarly, because the surface form of the task was based on soccer, the pre-experimental questionnaire also measured interest in soccer, which then served as a covariate in the major analyses.
The measures used were as follows. For beliefs about gambling, we used the Drake Beliefs About Chance Inventory (DBC; Reference Wood and ClaphamWood & Clapham 2005), a 22-item questionnaire that is organised into two scales, one relating to superstitious beliefs (DBC-Secondary) and the other to more conventional erroneous beliefs about chance events (DBC-Primary; see Appendix A.1). To measure interest in soccer, we asked people to rate their interest on a five-point Likert scale (see Appendix A.1).
3.2 The experimental manipulation
The independent variable, success-slope, was manipulated across four between-subjects conditions. In the “descending” condition (N = 85), early wins were followed by a string of losses. For the “ascending” condition (N = 79), the opposite was the case, and in the “flat” condition (N = 84), wins were approximately evenly distributed across the playing session. The “U-shaped” condition (N = 86) featured a concentration of wins at the beginning and at the end. In all conditions, participants experienced a win on 8 of the 48 trials.
3.3 The soccer-themed gambling task
The experimental task was a soccer-themed computerised task modelled after a slot machine in several respects: the option to bet on the results of multiple trials corresponded to the option to vary the number of lines played on a slot machine; there were more near misses than far misses; sound effects corresponded to those heard on slot machines; and bet and win-amounts for each betting option were calibrated to result in a long-term loss of 10% of used money, the return rate on South Australian slot machines.
The task instructions, issued verbally and in writing at the start of the session, emphasised that the task operated on the same principles as real slot machines, and that any credits won during the game would be exchanged for cash at the end. Participants played the game for a compulsory 48 trials, with any additional rounds being voluntary. Participants began the task with 5000 credits, which, they were informed, was equivalent to $AUD5.
An overview of the experimental task is shown in Figure 1. Each trial of the task displayed an on-screen soccer player taking a free kick, and participants were required to bet on the player scoring a goal. Several betting options were available, including some options that involved betting on the results of multiple trials (e.g., that the player would score three times in a row; Screen 2 in the figure). Other choices were also required. First, at the start of the game, participants were required to choose from among four different real-world players, each of whom had an entertaining biography provided (Screen 1). A change of player profile could be made after any round. Also, on each trial, participants chose which of the four corners of the goal the player kicked towards, a “random” option also being available (Screen 3). None of these choices influenced the outcome sequence, which was fixed for the first 48 trials in all four experimental conditions.
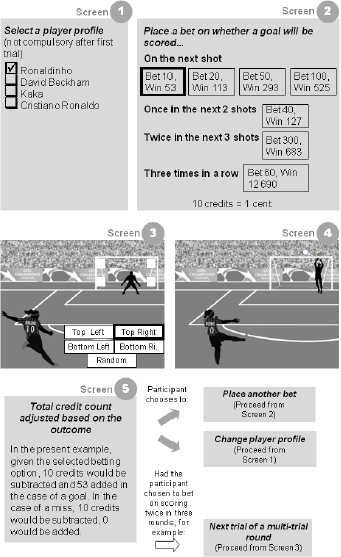
Figure 1: Experimental task interface
The outcome itself was displayed as an animation showing a goal being scored or a miss (Screen 4). The ball was shown to move in the direction that the participant selected, with a random number generator determining, on a trial-by-trial basis, whether or not the outcome was shown to be “close”. For example, for misses, the randomly-generated number determined whether the shot was shown to be a near-miss caught by the goalkeeper, or a far miss well clear of the goal posts.
The animation was followed by confirmation of the outcome, sounds of applause in the event of a goal, and adjustment of the credit count (Screen 5). Credits were subtracted in each round, and added whenever a goal or multiple goals were scored in line with the chosen betting option.
3.4 The post-experimental questionnaire
After participants completed the experimental task, we administered a questionnaire designed to elicit their conclusions about the task. It is from this questionnaire that our dependent measures were constructed.
To measure perceived control, we presented participants with the 15 items outlined in Table 1, and used factor analysis to reduce these 15 manifest variables to two latent variables, which (as outlined in the Results) loosely correspond to illusory primary and secondary control. These two variables formed our dependent measures for the two kinds of illusory control.
Table 1: The main measure of inferred control in the post-experimental questionnaire (Reference Ejova, Delfabbro, Navarro, Christensen, Schier and SuttonEjova, Delfabbro & Navarro, 2010).

Statement order was randomised for each participant.
α Statements added to the set used by Reference Ejova, Delfabbro, Navarro, Christensen, Schier and SuttonEjova, Navarro and Delfabbro (2010).
The other dependent measures related to success-frequency. The retrospective success-frequency item asked people to state the percentage of shots that resulted in goals, whereas the prospective success-frequency item framed the question in terms of the percentage of successes the participant would expect to see if the task were continued (see Appendix A.3). For the retrospective item, the question was framed in terms of number of wins for half the participants, and in terms of the number of losses for the other half (for data analysis, we converted all responses to the “wins” format by subtracting responses in the loss frame from 100).
The final component of the post-experimental questionnaire was a manipulation check item, intended simply to verify that participants noticed the success-slope to which they were exposed. Responses to this question confirmed that the manipulation was successful, especially in the “descending” condition, where 78% of participants indicated that “noticeably more wins occurred at the beginning” (see Appendix A.4 for more details).
3.5 Additional methodological details
Three additional methodological details are worth noting. Firstly, we wished to check that participants understood the instruction that the task was a gambling game rather than a solvable video game. To this end, the post-experimental questionnaire contained a yes/no question about whether a strategy was used. Those answering affirmatively were asked to describe the strategy. Participants, on the whole, could be concluded to have understood the instruction if some of the described strategies reflected reasoning typically observed in the face of random outcomes—gambler’s-fallacy-type reasoning (e.g., increasing bet amounts after a number of losses in expectation of an imminent win; Reference Tversky and KahnemanTversky & Kahneman, 1974). As a listing of the strategies in Appendix C shows, a substantial number of described strategies appeared to be informed by the gambler’s fallacy.
Secondly, to conceal the purpose of the experiment from participants, the pre- and post-experimental questionnaires contained distractor items in addition to the theoretically interesting ones mentioned earlier. A mood questionnaire (Reference Lorr and WunderlichLorr & Wunderlich, 1988) was included in both the pre- and post-experimental questionnaires, and the post-experimental questionnaire required Likert or 10-point-scale-based ratings of enjoyment of the game, strength of experienced emotional responses, and the extent to which the player profile feature and sound effects added to or reduced enjoyment. For the sake of brevity, we do not describe or analyse these items.
Finally, debriefing focused on explaining that none of the task’s choice features (player profiles, kick directions, betting timing) influenced outcomes. We also took care to check whether our participants were at risk of experiencing gambling problems. To that end, the pre-experimental questionnaire also included the Problem Gambling Severity Index (Reference Ferris and WynneFerris & Wynne, 2001). If a participant’s responses indicated that a risk of problem gambling existed, this was surreptitiously communicated to the experimenter via the colour of the on-screen message displaying the cash-out amount to be paid to the participant. Debriefing for these participants additionally involved providing them with an information sheet with help-service contact numbers.
4 Results
4.1 Estimating inferred control
As noted in the previous section, we used a 15-item question (Table 1) to assess participants’ inferences about control, and used factor analysis to reduce responses to two theoretically interpretable latent variables. Reference Ejova, Delfabbro, Navarro, Christensen, Schier and SuttonEjova, Navarro and Delfabbro’s (2010) procedure for doing this was followed, with the items first being screened for sufficient variability and intercorrelation. Given that this analysis was complex and is not the central topic of investigation, details are relegated to Appendix D, and only a brief overview is provided here. Two items (9 and 15) were removed from the analysis because their correlations did not appear robust. The remaining 13 items loaded naturally onto two factors. The first factor consists of items 1-8, and can be interpreted as primary control, insofar as it consists of statements that refer to strategies and game features. Items 10–14 form a factor that resembles secondary control, inasmuch as it is defined by statements referring to luck and its sensitivity to deservingness. The factors were highly correlatedFootnote 2.
In addition to estimating the factor loadings of each item on the two latent variables, we calculated the factor scores for each participant. These scores correspond to the score that each participant is estimated to have on the latent variables. Specifically, because our two latent variables were correlated, we computed regression factor scores, an aggregate score suitable for describing an individual’s position on correlated factors (Reference DiStefano, Zhu and MîndrilăDiStefano, Zhu & Mîndrilă, 2009).
For the purposes of subsequent analyses, note that the regression factor scores standardised to a mean of zero, so negative factor scores indicated lower ratings on the statements associated with the factor, while positive scores indicated greater endorsement (greater inferred control). The distributions of both primary and secondary control factor scores were highly positively skewed (skew = .73 and .67, respectively), and had standard deviations of .96 and .92, respectively. It is these factor score variables that we use as our measures of perceived control in subsequent analyses.
4.2 Inferred control across success-slopes
To test the direction of the success-slope effect, scores on the two perceived control measures produced by the factor analysis were examined across success-slope conditions. This involved analyses of covariance (ANCOVAs) with success-slope condition as the predictor and two covariates: soccer interest and slot-machine beliefs as measured by the DBC. The “Primary” scale of the DBC, relating to non-superstitious beliefs about chance, was the covariate in the analysis of the perceived primary control measure. Correspondingly, the DBC’s “Secondary” scale, concerned with superstitious and supernatural beliefs, was the covariate in the analysis of perceived secondary controlFootnote 3.
The degree of perceived primary control was found to vary as a function of success-slope (F(3,328) = 1.95, p = .03 pη2 = .03) once the substantial effect of slot-machine beliefs (DBC-Primary) was controlled for (F(1,328) = 120.21, p < .001, pη2 = .27)Footnote 4. Figure 2 shows the estimated means for primary control when DBC-Primary was set to a constant (mean) valueFootnote 5. As the distribution of means suggests, and as was confirmed by post-hoc tests with Bonferroni adjustment of the familywise α -level to .05, the estimated primary control mean was greater in the “ascending” condition relative to the “descending” condition (p = .04).
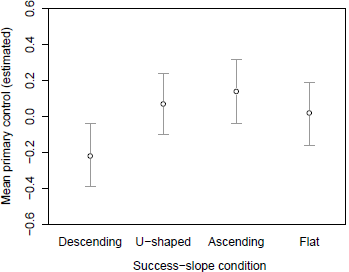
Figure 2: Estimated means (and 95% CIs) of inferred primary control across success-slope conditions when covariates were evaluated at their mean values.
Perceived secondary control was not affected by success-slope, but was predicted by slot-machine beliefs (F(1,328) = 114.63, p < .001, pη2 = .26). Thus, the crucial result pertained to perceived primary control, with the “ascending” condition producing stronger inferences than the “descending” condition.
To formally test the widespread methodological assumption that estimated success-frequency is a suitable proxy for control, success-frequency estimates (retrospective and prospective) were examined for their pattern across success-slope conditions. This pattern could then be compared to that observed for inferred primary control.
Since success-frequency estimates on both measures were not normally distributed (as is typical with count data), the analysis of responses to each measure across success-slope conditions involved fitting a generalised linear model with an assumed negative binomial distribution and log link function. Gambling-related beliefs (DBC-Total) and soccer interest served as covariates in both analyses, and the analysis of retrospective frequency estimates had question framing (frequency of “goals” vs frequency of “misses”) as an additional predictor. The analyses were conducted using IBM SPSS Statistics 19.
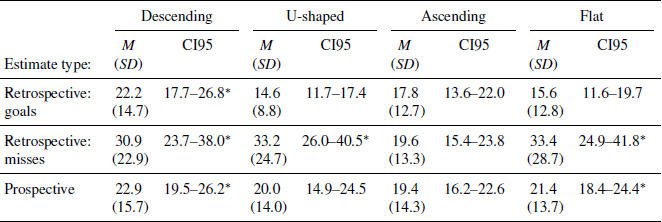
Estimates of retrospective success-frequency were found to be influenced by question framing (Wald χ2(1) = 21.32, p < .001) but not success-slope (Wald χ2(3) = 5.23, p = .16) or the interaction between framing and success-slope (Wald χ2(3) = 6.82, p = .08). Table 2 shows the estimates across success-slope conditions, broken down according to question frame. It can be seen that, across all conditions, estimates were higher when the question referred to “misses”. As far as the effect of success-slope itself is concerned, the table shows that there was a trend towards higher estimates in the “descending” condition relative to the “ascending” condition. This trend is in the opposite direction to that observed for inferred control ratings. To highlight this contrast, Figure 3 complements Figure 2 in showing mean retrospective success-frequency estimates across conditions, adjusted for covariates.
Table 2: Mean remembered success-frequency estimates across success-slope conditions.
* CI contains only values above the objective baseline success-frequency (16.7%), suggesting general overestimation.
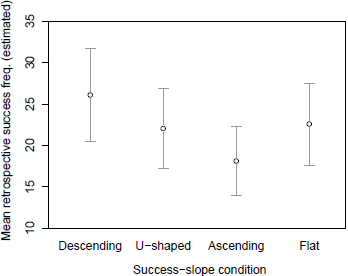
Figure 3: Estimated means (and 95% CIs) of retrospective success-frequency estimates across success-slope conditions when covariates were evaluated at their mean values.
Estimates of prospective success-frequency also did not differ significantly across experimental conditions (Wald χ2(3) = 1.31, p = .72), but showed the same general trend of higher estimates in the “descending” condition. The means of the prospective estimates across conditions are shown in Table 2.
Success-frequency estimates showed additional notable regularities across conditions, as can be seen in Table 2. Namely, answers to the retrospective question in the “miss” framing were largely overestimations of the objective success-frequency (1/6 = 16.7%). A further regularity was a general tendency towards overestimation in the “descending” and “flat” conditions.
5 Discussion
5.1 The success-slope effect
The main goal of this study was to determine which success-slopes produce stronger post-experimental inferences of illusory control. The results suggested that perceived primary control is largest in the “ascending” condition and lowest in the “descending” condition, with the “flat” and “U-shaped” conditions lying in the middle.
The fact that the “ascending” condition produced the strongest inferences of control is broadly consistent with Reference MatuteMatute’s (1995) proposal that experiencing an increasing rate of successes can create the false impression of learning the correct strategy. The findings can alternatively be interpreted as evidence that experiencing a decreasing win rate in the “descending” condition leads to an accurate perception that no learning is occurring. Specifically, the “descending” condition might provide participants with a strong signal that whatever strategy they are attempting to employ does not work. After all, the participant is presumably trying to produce the successes, but in the “descending” condition the rate of such successes declines over time, making it very clear that these attempts have been unsuccessful.
5.2 Primary and secondary control
A second goal of the study was to employ more refined measures of the extent to which people perceived themselves to be in control of the outcome. In this respect, the outcomes are a little more mixed. On the positive side, the factor analysis did suggest that there are two distinct (but correlated) kinds of beliefs about control involved, consistent with Reference Rothbaum, Weisz and SnyderRothbaum et al. (1982) and Reference Ejova, Delfabbro, Navarro, Christensen, Schier and SuttonEjova et al. (2010). Moreover, it is reassuring to see that our measure of primary control within a complicated and realistic task produced a success-slope effect consistent with the results of a previous study that used a simpler design (Reference MatuteMatute, 1995). These results suggest that the success-slope effect is not an artefact of a particular way in which questions about perceived control are worded, nor is it restricted to simplistic experimental designs.
On the negative side, part of our motivation for using richer measures of perceived control in the context of a rich and complicated task was to see if we could detect any interesting effects for secondary control. As noted in the Introduction, in real world gambling situations, people do make claims about secondary control. People often refer to “luck” as an entity that can be on the gambler’s side, for instance (e.g., Reference Keren and WagenaarKeren & Wagenaar 1985). This is partly reflected in our results, to the extent that the degree of secondary control that participants reported in our task did correlate with their score on the relevant scale of the Drake Beliefs about Chance questionnaire. However, we did not uncover any evidence for a success-slope effect with respect to secondary control.
5.3 Memory versus inferred control
One of our major concerns outlined in the Introduction was the possibility that asking people what they remember about outcome frequency is not a good substitute for asking them about the amount of control they perceived over that outcome. This concern was borne out, in that, unlike ratings of inferred control, estimates of remembered success-frequency were found not to be affected by success-slope. Moreover, the success-frequency estimates displayed trends consistent with those observed in the memory literature. For instance, studies of memory point to a “spacing effect”—consistently better memory for stimuli more distributed across time (e.g., Reference Glenberg, Bradley, Kraus and RenzagliaGlenberg, Bradley, Kraus & Renzaglia, 1983; Reference Varey, Mellers and BirnbaumVarey, Mellers & Birnbaum, 1990). The fact that we observed higher estimates in response to the “miss” framing of the retrospective success-frequency question (“What percentage of the shots you kicked over the course of the game resulted in misses?”) is consistent with this effect. Specifically, misses might have been remembered more poorly than goals because they were less widely spaced, with reverse-scoring of responses, therefore, producing overestimations.
Similarly, what has been termed an “over-under effect” might have been operating in all conditions, manifesting itself in overestimation rather than accurate recall in the “descending” and “flat” conditions, and in accuracy rather than underestimation in the other two conditions. The effect refers to the tendency to overestimate low event frequencies and underestimate high ones (e.g., Reference BeggBegg, 1974; Reference ErlickErlick, 1964; Reference Fiedler and ArmbrusterFiedler & Armbruster, 1994; Reference Lichtenstein, Slovic, Fischhoff, Layman and CombsLichtenstein et al., 1978). Background beliefs about the task determine what constitutes “low” and “high” frequencies (Reference Lichtenstein, Slovic, Fischhoff, Layman and CombsLichtenstein et al., 1978), so, given participants’ beliefs about gambling and soccer, it is possible that the success-frequency of 1/6 was low in the context of the soccer task. The resultant upwards-adjustment of estimates in all conditions could have produced the observed pattern in the following ways. In the “flat” condition, the “spacing effect” could have produced accurate estimates, which were adjusted upwards to result in the observed overestimation. In the “descending” condition, the well-known “primacy effect”, involving better memory for items and events at the beginning of a sequence (e.g., Reference MurdockMurdock, 1962), could have resulted in accurate estimates, which were then adjusted upwards to produce the observed overestimation. In the “U-shaped” condition, the “primacy effect” would have been weaker because there were fewer target items (successes) to remember at the beginning of the sequence. Likewise, in the “ascending” condition, there were no target items at the beginning of the sequence, so a “primacy effect” could not occur. Thus, in these conditions, memory for successes might have been poorer but estimates might have been adjusted upwards as part of the “over-under effect”, resulting in the observed accuracy.
A “recency effect”, involving better memory for the last items in a sequence, has also been widely documented and might have been expected to manifest itself in higher estimates in the “U-shaped” and “ascending” conditions. However, the “recency effect” is easily disrupted by interference tasks (e.g., Reference Glanzer and CunitzGlanzer & Cunitz, 1966), which, in this experiment, occurred between the end of the experimental session and the time when the success-frequency question was answered.
Of course, these memory-based explanations for the success-frequency findings are only speculative and require formal testing. However, the extent to which our results appear to agree with the memory literature does suggest that success-frequency estimates in illusion of control studies have, to date, reflected memory of the number of obtained wins rather than inferences about how wins can be obtained.
5.4 Directions for future research
One direction for future research could involve testing competing explanations for our main result—the finding that the “ascending” condition had higher associated inferred control levels than the “descending” condition. Reference MatuteMatute (1995) obtained a similar finding and interpreted it to mean that participants in the “ascending” condition believed that they had learned the “correct” response. An alternative interpretation is that experiencing a declining success rate in the “descending” condition caused participants to accurately perceive that no learning was occurring. Testing Matute’s explanation would involve observing behavioural patterns over time, as Matute did in finding that participants in the “ascending” condition were more likely to repeat the same response or response sequence during the last trials of the task. Analogously, in our experimental task, if Matute’s interpretation is correct, the “ascending” condition should give rise to declining rates of player-profile change and kick-direction variability over time.
Our findings also raise questions regarding the illusion of secondary control. One issue is that the fine details of the factor analysis used to establish the illusion of secondary control as a separate construct differed slightly from those in the study by Reference Ejova, Delfabbro, Navarro, Christensen, Schier and SuttonEjova et al. (2010; see Appendix C). The task for future research is to adjust the wording of the perceived-control measure to form a measure of inferred primary and secondary control that can be applied consistently across studies. Since the illusion of secondary control was found not to vary as a function of success-slope, another task for future research is to identify other factors that might influence this variant of the illusion. The degree of choice available in the gambling task has been suggested as a possibility. Specifically, it has been suggested that greater opportunities for choice allow for a wider range of magical or superstitious beliefs to be applied in generating playing strategies (Reference Rothbaum, Weisz and SnyderRothbaum, Weisz & Snyder, 1982; Reference Wohl and EnzleWohl & Enzle, 2002). For example, in our experimental task, the availability of a player profile choice option featuring famous soccer players allowed participants to select a “lucky” player. Removing this feature or using less well-known players should, by this logic, lead to a reduction in perceived secondary control.
Future research could also set out to test our speculative claims about the memory effects underlying the observed pattern of success-frequency estimates across success-slope conditions. Specifically, one hypothesis was that an “over-under effect” (the tendency to overestimate the baseline success-frequency because it was only 1/6) operated in all conditions. This claim could be verified by obtaining success-frequency estimates across different objective success frequencies within the soccer-themed task and observing (a) whether lower frequencies are consistently overestimated while higher frequencies are consistently underestimated, and (b) whether 1/6 is among the “lower” (i.e., overestimated) frequencies. A second claim was that “recency effects” (better memory for events late in the sequence) disappeared in the “ascending” condition due to the time that elapsed between the end of the task and the presentation of success-frequency questions. This hypothesis can be tested by investigating whether the “ascending” condition produces higher success-frequency estimates when questioning is immediate rather than delayed.
Appendix A: Measures and procedure
A.1: Pre-experimental questionnaire
Drake Beliefs About Chance Inventory (DBC; Wood & Clapham, 1995)
Illusion of Control scale (DBC-Primary)
1. Wins are more likely to occur on a hot machine.
2. The more familiar I am with a slot machine game, the more likely I am to win.
3. It is good advice to stay with the same pair of dice on a winning streak.
4. Show me a gambler with a well-planned system and I’ll show you a winner.
5. If a coin is tossed and comes up heads ten times in a row, the next toss is more likely to be tails.
6. There are secrets to successful slot machine, roulette and dice gambling that can be learned.
7. One should pay attention to lottery numbers that often win.
8. A good slot machine, roulette or dice gambler is like a sportsperson who knows winning plays and how to use them.
9. Some gamblers are just born lucky.
10. The longer I’ve been losing, the more likely I am to win.
11. I will be more successful if I have a system to play the slot machines.
Superstition scale (DBC-Secondary)
1. There may be magic in certain numbers.
2. I can improve my chances of winning by performing certain special rituals
3. There is useful information in my daily horoscope.
4. Playing slot machines is a form of competition between the player and the machine.
5. I believe that fate is against me when I lose.
6. A game of chance is a contest of wills between the game and the player.
7. When I take a test (or took them in the past) I use a lucky pen or pencil.
8. When I need a little luck I wear lucky clothes or jewellery.
9. I consider myself to be a superstitious person.
10. I like to carry a coin, charm or token when I’m doing something important.
11. I have a special system for picking lottery numbers.
Soccer Interest
To what extent are you interested in soccer? (0) Very strongly, (1) Strongly, (2) Mildly, (3) Very little, (4) Not at all
A.2: Task instructions
Verbal and written instructions issued to participants upon arrival
There has been some speculation about the nature of psychological responses to themed gambling tasks, such as slot machine games based on well-known board games or sports. This study is concerned with your impressions of a soccer-themed gambling task we have designed for use in future research on this issue. The task operates on exactly the same principles as a slot machine, but looks slightly different because it has been adapted for the university laboratory, a setting that lacks the lights, sounds, and social atmosphere of real gambling venues.
Participation in the experiment will involve completing a preliminary questionnaire about your gambling-related and soccer-related experiences, playing the computerised soccer-themed gambling game, and completing a questionnaire about your impressions of the gambling task.
On-screen instructions presented after completion of the pre-experimental questionnaire
You are now ready to play the soccer-themed gambling game itself! The game possesses the essential features of a slot machine game, but these features are embedded in a gaming environment that is thematically more interesting than standard slot machine games.
Here are the basic rules of the game… You will start the game with $5 worth of credit. In each round, you will be able to choose how much credit to bet on whether a goal (or a set of goals) will be scored by a soccer player shown on the screen. Apart from the bet amount, you will also be asked to choose a player profile and the direction in which the ball will be kicked.
A.3: Post-experimental questionnaire
Inferred control
Supplementary yes/no strategy measure:
Did your experience of the game suggest to you that you could draw on a strategy to produce goals when you needed them?
If yes, briefly describe your strategy.
Remembered success-frequency
Retrospective goals (for a random half of participants)
As far as you can remember, what percentage of the shots you kicked over the course of the game resulted in goals?
Retrospective misses (for a random half of participants)
As far as you can remember, what percentage of the shots you kicked over the course of the game resulted in misses?
Prospective
If you were allowed to kick another 100 shots in the game, on how many of those shots do you think you would score a goal?
A.4: Post-experimental questionnaire: manipulation check
Item
As far as you can remember, what is the best way to describe the overall sequence of kick outcomes you experienced during the game?
-
• Wins were relatively evenly spaced out across rounds;
-
• Noticeably more wins occurred at the beginning;
-
• Noticeably more wins occurred during the middle rounds;
-
• Noticeably more wins occurred at the end;
-
• Noticeably more wins occurred at the beginning AND at the end.
-
• Other (please specify)
Findings
In the “descending” condition, the correct answer of “Noticeably more wins occurred at the beginning” was offered by 78% of participants. In the “ascending” condition, 55% reported experiencing most wins at the end, and 24% in the middle rounds. Among participants in the “flat” condition, 42% correctly recalled that “wins were relatively evenly spaced across rounds” and 25 % reported the wins to have been concentrated in the middle rounds. In the “U-shaped” condition, 47% reported seeing most wins in the beginning, 26% reported an even spread, and 15% correctly identified their sequence as having featured “more wins at the beginning AND at the end”.
Appendix B: The experimental manipulation
Participants experienced one of three possible outcome sequences in each success-slope condition. In generating the “descending” sequences, it was decided that the four 12-trial blocks comprising 48 trials would feature four, three, one, and zero wins, respectively. Numbers from one to 12 were then randomly generated without replacement to determine the exact position of the winning trials. Three different sequences were created in this way and Table B.1 shows one of them.
The “flat” and “U-shaped” sequences were created in a similar manner, subject to the constraint that “flat” sequences would be characterised by two wins per 12-trial block, while the “U-shaped” sequences would feature three wins in the first and last blocks, and one in each of the middle blocks. The “ascending” sequences were obtained, simply, by flipping the “descending” sequences.
Table B.1 An example of the outcome sequences experienced in the four success-slope conditions.

Appendix C: Factor analysis and preliminary screening of inferred control measure
Before submitting responses on the inferred control measure (“To what extent would you use each of the following statements to describe the reason for your successes?”) to a factor analysis, two preparatory steps were taken. First, responses were checked for sufficient variability, as reflected in the frequency of non-zero ratings. The distribution of responses is summarised in Table C.1 and is almost identical to that obtained in our earlier study (Reference Ejova, Delfabbro, Navarro, Christensen, Schier and SuttonEjova, Delfabbro & Navarro, 2010). On average, approximately 60 percent of the ratings provided for each statement were not zero. The newly-introduced “Bet options” statement (9) was distinct in attracting non-zero ratings from 80 percent of participants.
Table C.1 Distribution of responses to statements comprising the inferred control measure (N = 334).

# 21 of these Ss provided zero ratings on all other statements.
The second preparatory step, also conducted in the pilot study, was a screening procedure aimed at identifying statements correlating with other statements due solely to inter-correlating zero ratings. The procedure is as follows. Starting with the statement that attracted the most zero ratings, select only those participants who did not provide a zero rating for that statement. If, in this select dataset, the Spearman correlations of the statement with other statements become largely non-significant, exclude the statement from the subsequent factor analysis. The application of this procedure led to the exclusion of the “Chance” statement (15). While non-zero ratings on other statements correlated with ratings on a minimum of four statements (p < .01), non-zero ratings on this statement did not correlate with any statement ratings.
For the 14 retained statements, an examination of initial communalities led to the further exclusion of the “Bet” statement (9) from the factor analysis. For the remaining statements, a Principal Axis Factoring (PAF) analysis was carried out upon ascertaining factorability (KMO = .94; Bartlett’s test: χ2(78) = 2130.11, p < .001; initial communalities shown in Table C.2.). Various criteria for extracting factors (eigenvalues greater than one, point of inflection on the scree plot and parallel analysisFootnote 6) suggested a two-factor solution (Reference Hayton, Allen and ScarpelloHayton, Allen & Scarpello, 2004), so two factors were extracted.
Table C.2 For the 13 retained statements of the inferred control measure, initial communalities and factor loadings and communalities after extraction produced by a PAF analysis with oblimin rotation (N = 344).

Note: Factor loadings <.3 are suppressed.
The factor loadings of statements following direct oblimin rotation (Reference Costello and OsborneCostello & Osborne, 2005) are shown in Table C.2. In line with the pilot findings, statements relating to practice (1), skill (3), computer games (4), and strategy (7) clustered together in loading on a primary control factor (Factor 1). This factor also came to be defined by the “Goalkeeper” (2) and “Player profile” (8) statements, which had loaded on secondary control in Reference Ejova, Delfabbro, Navarro, Christensen, Schier and SuttonEjova et al. (2010). The newly-introduced statement about kick direction choices (5) also loaded on this factor, and the final statement comprising the factor was the “Soccer knowledge” statement (5), which was excluded from Reference Ejova, Delfabbro, Navarro, Christensen, Schier and SuttonEjova et al.’s (2010) factor analysis because it attracted the highest number of zero ratings. Factor 2 corresponded to an inferred secondary control latent variable in consisting of the four luck-related statements (11–14) and the “Deserving to win” statement (10). The two factors were strongly correlated (r = .73).










