1 Introduction
People often find themselves having to estimate or re-evaluate how much time it should take them to complete an activity, after they have already begun the activity. This estimation often includes an intuitive judgment of how much time they would save if they increase their speed. For example, drivers who wish to arrive at their destination earlier than the expected time need to judge the impact a speed increase will have on their journey time. In general, even before starting out, drivers regularly select speeds and routes that may save enough time so that they arrive on time or early (e.g., Reference TarkoTarko, 2009). Similarly, when managers are deciding how to allocate company resources in order to increase productivity, they sometimes make intuitive choices between different time-saving options (e.g., Reference SvensonSvenson, 2011).
Time-savings judgments are, however, systematically and predictably biased. Most studies on individuals’ intuitions of time-savings have focused on driving situations, asking drivers to estimate the time that could be saved given various speed increases (Reference Fuller, Gormley, Stradling, Broughton, Kinnear and O’DolanFuller et al., 2009; Reference PeerPeer, 2010a, 2010b, 2011; Reference Peer and SolomonPeer & Solomon, 2012) or to choose between different time-saving options (Reference SvensonSvenson, 1970, 1973, 2008, 2009). These studies found that drivers make erroneous estimations about how much time they can save if they increase their speed. Specifically, the drivers in these studies overestimated the time that could be saved when increasing from a relatively high speed and underestimated the time that could be saved when increasing from a relatively low speed. For example, when asked to judge which of two road improvement plans would be more efficient in reducing mean journey time, respondents preferred a plan that would increase the mean speed from 70 to 110 kph more than a plan that would increase the mean speed from 30 to 40 kph, although the latter actually saves more time (Reference SvensonSvenson, 2008).
Researchers have shown that such biased judgments of time-savings lead to poor speed choices and decisions. Drivers who misestimated the time saved when increasing from a low or high speed also misestimated the speed required for arriving at a specific time and chose unduly high speeds, sometimes even exceeding the legal speed limit (Reference PeerPeer, 2010a, 2011). In one study, when drivers were asked to estimate the time saved when increasing from 40 to 50 kph for a 10-km journey, on average they estimated it to be about 4.5 minutes (when in reality it is 6 minutes)—a significant underestimation of about 25%. Subsequently, these high-biased drivers judged that the required speed for completing the journey in 20 minutes as about 65 kph—a significant overestimation of the actual 50 kph required speed (Reference PeerPeer, 2010a). These results were replicated using higher or lower speeds, larger or shorter distances and different modes of presenting the questions as well as the response options (Reference PeerPeer, 2010b).
Similar biased judgments emerge in other contexts as well such as when people estimate savings in patients’ waiting time as part of the decision whether to add more physicians to a healthcare center (Reference SvensonSvenson, 2008) or when estimating the increase in the productivity of a manufacturing line by adding more workers (Reference SvensonSvenson, 2011). In one study, participants, asked to decide which of two alternative production speed improvements would save the most production time, preferred an option that increases production from 50 to 120 units per hour over an option that increases production from 30 to 60 units per hour, although the latter actually saves more time (Reference SvensonSvenson, 2011).
This “time-saving bias”, we argue, is mainly attributable to people’s inability to grasp the actual curvilinear relationship between increasing speed and the reduction of activity time. Specifically, this inability results from how speed is usually presented, as distance or units completed per a fixed time (i.e., mph or kph in driving or units per hour in manufacturing). In this paper, we illustrate the curvilinear relationship between speed and time and demonstrate how individuals’ time-saving bias could be reduced when speed information is converted into a more intuitive measure of pace (e.g., the time required to complete a fixed distance). We focus mainly on the context of driving because it is a common and ubiquitous situation in which many adults face on a frequent basis.
1.1 The curvilinear relationship between speed and time
The physical formula for calculating the time gained when increasing driving speed is:
where t is the time gained, c is constant and used to transform between units of measurement, D is the distance traveled and V 1 and V 2 are the original and increased speeds, respectively. As can be seen in Figure 1, the relationship between increasing speed and journey duration is curvilinear: as speed increases, the time required to complete a given journey (for example, of 10 miles), decreases in a non-linear fashion. This curvilinear relationship results in the fact that a similar speed increase would result in more time saved when initiated at a low speed compared to when starting from a higher speed. For example, when increasing from 20 to 30 mph, the time required to complete 10 miles decreases from 30 to 20 minutes, saving 10 minutes. The same speed increase of 10 mph would result in less time saved if the initial speed is higher (e.g., only 2 minutes saved when increasing from 50 to 60 mph).
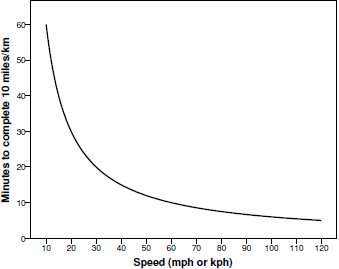
Figure 1: The curvlinear function of pace by speed: The time (in minutes) required to complete a 10-mile or 10-km journey in miles per hour or km per hour, respectively.
Several studies have shown that people’s lay judgments do not conform to this curvilinear relationship. Reference SvensonSvenson (2008) suggested that people’s judgments of time-savings actually follow a Proportion heuristic, by which people judge the time saved as the proportion of the speed increase from their initial speed. In his study, when asked to choose an alternative that would save more time, most participants preferred an increase from 80 to 130 kph over an increase from 40 to 50 kph, presumably because the proportion of the speed increase from the initial speed is higher in the first option. In reality, the second option saves more time (Reference SvensonSvenson, 2008). Reference SvensonSvenson (2008), proposed the following formula to predict poeple’s responses accordign to this Proportion heuristic:
where t is the time gained, c is constant and used to transform between units of measurement, D is the distance traveled and V 1 and V 2 are the original and increased speeds, respectively. According to this model, people judge the time saved (or lost) when increasing (or decreasing) speed as a function of the proportion of the increase in speed (the difference between the higher and initial speed) from the higher speed (Reference SvensonSvenson, 2008).
Another recent study offered a refinement to this formula, suggesting that people use the proportion of the increase in speed from the initial, rather than higher, speed (Reference Peer and GamlielPeer & Gamliel, 2012). According to this model, people judge time savings in a more linear fashion, and thus we call it the Linear heuristic. The formula describing this model is:
where t is the time gained, c is constant and used to transform between units of measurement, D is the distance traveled and V 1 and V 2 are the original and increased speeds, respectively. In that study, more of participants’ non-normative responses followed this Linear heuristic (termed “Difference heuristic” in Reference Peer and GamlielPeer & Gamliel, 2012) than the Proportion heuristic (Reference Peer and GamlielPeer & Gamliel, 2012; also see Reference PeerPeer, 2010b). Generally, it seems that people falsely believe that journey duration decreases somewhat linearly as driving speed increases, irrespective of the initial speed, thereby causing the time-saving bias. Although it is still unclear which heuristic people use to estimate time savings, clearly, few follow the correct curvilinear relationship.
1.2 De-biasing the time-saving bias
One potentially successful method for de-biasing individuals could be derived by examining the solution to an analogous bias—the Miles-Per-Gallon (MPG) illusion, in which people misestimate the difference in gas consumption among vehicles with different MPG values. The MPG form of measuring fuel efficiency (most commonly used in the U.S.A.) has a biasing effect on people’s perceptions of the relation between a car’s MPG and the amount of gas it consumes: “People falsely believe that the amount of gas consumed by an automobile decreases as a linear function of a car’s MPG. The actual relationship is curvilinear. Consequently, people underestimate the value of removing the most fuel-inefficient vehicles” (Reference Larrick and SollLarrick & Soll, 2008, p. 1593). In contrast, when presenting fuel efficiency as the amount of gas consumed per given distance (e.g., gallons per 100 miles—GPM), respondents adequately assessed differences in cars’ fuel efficiency (Reference Larrick and SollLarrick & Soll, 2008).
We suggest that there is a close analogy between the MPG illusion and the time-saving bias because in both cases the actual relationship is curvilinear while people perceive it as linear. Thus, just as the MPG misconception was countered using the GPM measure, we suggest that using a pace measure could diminish the time-saving bias. By a pace measure we mean the amount of time it takes to complete a given distance at a given speed. For example, a speed of 10 mph is equivalent to 60 minutes per 10 miles, and the speeds of 20, 30, 40, 50 and 60 mph can be translated into 30, 20, 15, 12 or 10 minutes per 10 miles, respectively.
This pace measure offers several advantages over the traditional speed measure that might make it more intuitive and easier to use by lay people. First, it might reduce the cognitive complexity of estimating journey times at various speeds. For example, if the journey’s distance is 10 miles, all one has to do is identify the number of minutes it would take to complete the journey at the appropriate speed from Figure 2 (for example, driving at 30 mph would complete this journey at 20 minutes). If the journey is longer (or shorter) than 10 miles, one could simply multiply the pace value of a given speed as needed (for example, completing a 30 miles journey at 30 mph would take 20 X 3 = 60 minutes). These simpler calculations also help to compute the time saved when increasing from one speed to another. For example, while estimating the time saved when increasing from 30 to 40 mph (for 10 miles, for example) is usually a difficult task, when given pace data it becomes much simpler as one only needs to subtract the respective pace values (e.g., 20 minus 15 minutes per 10 miles = 5 minutes saved).
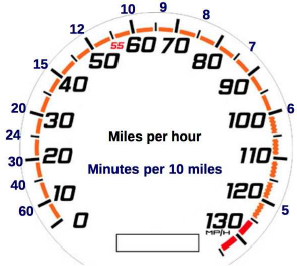
Figure 2: The “Paceometer”—A speedometer showing values of pace (minutes per 10 miles) at selected levels of speed (mph).
Thus, we conjectured that complementing conventional speed information (given as miles/km per hour) with the equivalent pace data (e.g., minutes per 10 miles/km) would improve people’s time-saving judgments. To test this, we designed a new “Paceometer”, adding to the regular speed measure the minutes that are required to complete a fixed distance of 10 miles (or 10 km) at selected levels of speed (see Figure 2). In three studies, half of the participants received this Paceometer while the other half received a regular speedometer without any pace data. We hypothesized that participants who would have pace data would solve problems of estimating journey time, time-saved and driving speed much better than the control group. Studies 1 and 2, in which only U.S. residents participated, used the mph version of the Paceometer and tested its effect on judgments of journey duration at various speeds, on estimations of time saved when increasing speed, and on estimations of the speed required to complete a given journey. Study 3 replicated Studies 1–2 using the kph version of the Paceometer with non-U.S. residents.
2 General method
In all studies, participants were randomly assigned to either the pace or speed conditions. In the pace condition, participants were shown an image of a Paceometer along with the following text (for the mph version):
Notice that in the image of the speedometer above, next to some speeds we added the number of minutes required to complete a 10-mile journey (on the outside circle, in blue). For example, driving at 60 mph means that a journey of 10 miles will take 10 minutes to complete and driving at 30 mph means that 10 miles will take 20 minutes to complete, etc. This image will appear in the following questions and you may use it to answer the questions.
In the speed condition, participants were shown an image of a regular speedometer along with the following text (for the mph version):
Notice that in the image of the speed meter above, we included speeds from 0 to 130 mph (miles per hour). As you probably know, the numbers on the speedometer indicate the amount of miles that can be completed in an hour at each speed. For example, if you drive at 60 mph for one hour, you will travel 60 miles, and driving at 30 mph for one hour, you will travel 30 miles. This image will appear in the following questions and you may use it to answer the questions.
The kph versions were similar except for the unit of measurement.
Participants completed an on-line survey that displayed the questions alongside either the Paceometer or a regular speedometer, according to the assigned condition. Participants in Studies 1–2 were recruited using Amazon Mechanical Turk (henceforth, AMT) and were pre-screened to include only U.S. residents, age 21 or above, holding a valid driving license for more than a year and who reported driving a vehicle regularly (at least three times a week). AMT participants were also required to have completed at least 1,000 previous tasks on AMT with a success rate of at least 95%. We used a customized script on AMT to make sure that none of the participants from Study 1 responded to Study 2. Participants in Study 3 were undergraduate students from an Israeli college, who met the same age and driving experience requirements specified above. Studies 1—3 used an attention-check question at the beginning of the survey (“what is your favorite sport?”) and participants were asked to ignore it and not select any option. Participants who selected an option were not allowed to participate in the study. In all the studies, we excluded participants whose responses violated the monotone relation between speed and time (e.g., indicated that driving at 50 mph would take more time than 30 mph or that time saved when increasing from 20 to 30 mph is higher than from 20 to 50 mph). The numbers of participants excluded from the analysis were 21, 27 and 17 (19%, 28% and 13%) in Studies 1, 2 and 3, respectively. These participants were similarly distributed among the two conditions. In addition, some of the participants did not complete all the problems (30, 13 and 8 [33%, 19% and 7%] in Studies 1, 2 and 3, respectively). Analyzing the results using only participants who completed all problems yielded similar results to the ones that are reported in each of the following studies.
3 Study 1
3.1 Method
Ninety-one AMT workers took part in the study (50 in the pace condition, 41 in the speed condition). In Problems 1 and 2, participants estimated the duration of a 10-mile journey at 10, 20, 30, 40, 50, 60, 70, and 80 mph and then the time a 30-mile journey would take at these speeds. In Problems 3 and 4 participants estimated, for a journey of 20 miles, the time that could be saved when increasing from 20 mph in increments of 5, 10, 15, 20, 25, 30, 35, and 40 mph and then increasing from 50 mph in the same increments. In Problem 5, participants estimated the time lost when decreasing from 60 mph in increments of –5, –10, –15, –20, –25, –30, –35, and –40 mph.
3.2 Results
For each question in each problem, we coded participants’ responses as correct if it was exactly as the value predicted by Formula (1), (when the value predicted by the correct formula (1) was not a round number [e.g., 8.53], we counted rounded-up and rounded-down numbers as correct as well [e.g., 8 and 9]). If the response was incorrect, we coded it as either an overestimation (if it was larger than the correct value) or an underestimation (if it was smaller than the correct value). We found high internal reliability between the questions in each problem (KR-20 = .85, .79, .92, .94, .85, for Problems 1—5, respectively) and thus we summed the number of questions, in each problem, in which a participant gave the correct response or over- or under-estimated. Figure 3 shows the comparison of the percentages of each of these types of responses between the pace and speed conditions in all of the five problems. In the following sections, we first analyze the differences in the propensity to provide correct responses between the conditions, and then analyze the differences in the non-normative responses as well.
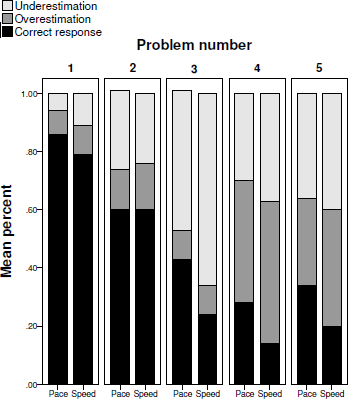
Figure 3: Percent of correct responses, overestimations and underestimations in each of the five problems of Study 1 in the pace and the speed conditions.
3.2.1 Normative responses
As can be seen, in four out of the five problems, participants in the pace condition gave correct answers in a higher percentage of the times: 85.87% vs. 78.57% in the first problem, 42.5% vs. 24.19% in the third problem, 28.02% vs. 13.75% in the fourth problem, and 33.7% vs. 20.09% in the last problem. The differences in percentages of correct responses between the groups ranged from 7.3% in the first problem to 18.31% in the third problem. We discuss the lack of difference between the conditions in Problem 2 (59.71% vs. 59.94%) in the following Discussion section.
To determine whether the effect of pace data on the propensity to provide correct responses was statistically different between the conditions, we ran a logistic regression on each of the problems, regarding the problem’s questions as fixed effects and including the condition and the interaction between the questions and the condition. In the first problem (estimating a 10 miles journey time), there was no statistically significant effect for either the condition, the questions or the interaction (Wald χ2 (1) = .38, .18, 2.62, p = .54, .67, .11, respectively). In the second problem (estimating a 30 miles journey time), we found a statistically significant effect only for the interaction (Wald χ2 (1) = 4.09, p < .05) but not for the condition or the questions (Wald χ2 (1) = 3.57, .59, p = .06, .44, respectively). The results for Problems 3 to 5 were much more conclusive as they all showed a significant effect for the condition (Wald χ2 (1) = 22.91, 4.68, 10.38, respectively, p < .05), but not for the questions (Wald χ2 (1) = .82, .34, .16, p = .37, .56, .69, respectively) or the interaction (Wald χ2 (1) = 2.53, .99, .63, p = .12, .32, .43, respectively). These analyses showed that participants in the pace condition had a significant advantage over those in the speed condition when estimating the time saved (or lost) when increasing (or decreasing) speed, and that this advantage persisted over the different questions within each problem, regardless of their individual level of difficulty.
3.2.2 Analyzing non-normative responses
We next analyzed participants’ non-normative (incorrect) responses to examine the rates of over- and under-estimations between the problems and between the conditions. We focused on the problems that examined time-saving estimations, because they were most pertinent to our study. In overall, the rates of over- or under-estimations typically followed the predictions of the time-saving bias and showed that participants underestimated the time saved when increasing from a low speed and overestimated the time saved when increasing from a relatively high speed. In the questions of increasing from a low speed (Problem 3), among the participants who gave incorrect answers, most underestimated the time that could be saved (87.2% in the speed condition and 83.3% in the pace condition). In the questions of increasing from a high speed (Problem 4), among the participants who gave incorrect answers, most overestimated the time that could be saved (57% in the speed condition and 58% in the pace condition). However, in the questions of decreasing from a high speed (Problem 5), the portion of participants who overestimated the time lost (50.3% in the speed condition and 54.3% in the pace condition) was similar to those who underestimated it.
We also examined participants’ responses to the time-savings problems and classified them as following one of the theoretical models we delineated in the Introduction. These included a) the Normative model—which included correct responses (those who gave the value predicted by Formula (1)); b) the Proportion heuristic—which included responses that followed Formula (2) (Reference SvensonSvenson, 2008); and c) the Linear heuristic—which included responses that followed Formula (3) (Reference Peer and GamlielPeer & Gamliel, 2012). Responses that did not fit any of these models were classified as “other”. For example, for the question “how much time would you save if you increase your speed from 20 to 40 mph (for a 20 miles distance)”, we coded correct answers (30 minutes) as “normative”, answers of 10 minutes as “Proportion” and answers of 20 minutes as “Linear” (remaining answers were coded as “other”). We did so only for the questions in which a clear distinction could be made between the predicted responses of the different models. For example, for the last question in Problem 3 (estimating time saved when increasing from 20 to 60 mph), both the normative and linear models predict the same answer (40 minutes), and were thus not included in this analysis. In the questions that were examined, we rounded participants’ responses to the closest value before classifying them to the models, to allow for small rounding errors.
For the first problem regarding time savings (Problem 3), we found that, in overall, about 67% of participants’ responses to the seven questions (excluding the last one) could be classified to one of the models. We also found a high reliability in the classification of participants’ responses to the models (Cronbach’s alpha = .91). We thus counted the number of responses that fit each model across the questions and averaged these scores. Table 1 shows the mean percentage of responses that fit each model between the pace and speed conditions. As can be seen, the percentage of normative (correct) responses was much higher in the pace condition, compared to the speed condition (57.56% vs. 19.82%). Additionally, while very few of the participants seemed to follow the Proportion heuristic in both conditions (1.26% vs. 3.69%), more responses especially in the speed condition, seemed to follow the Linear heuristic: 30.41% of the responses in the speed condition, vs. 10.5% in the pace condition, were predicted by this Linear heuristic model.
Table 1: Percentages of responses classified to the different models in the two conditions.
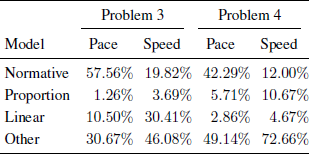
The models were much less effective for Problem 4. First, we had to ignore the responses to the first three questions (about increasing from 50 to 55, 60 or 65 mph), because the predicted values of the three models were too similar (e.g., 4.36, 3.64, and 4, for the normative, proportion and linear models, respectively, for the first question). Analyzing the responses to the remaining five questions (about increasing from 50 to 70, 75, 80, 85 or 90 mph) showed that, in overall, only 40% of participants’ responses could be classified to one of the models, although the internal reliability was rather high (Cronbach’s alpha=.90). Still, the pace condition’s advantage was clear, as 42.29% of the responses in that condition followed the correct, normative, model, while only a few followed either the Proportion or Linear heuristics, compared to only 12% of normative responses in the speed condition. Most of the non-normative responses in this problem did not seem to follow either the Proportion or the Linear heuristics: only 10.67% in the speed condition, and 5.71% in the pace condition, followed the Proportion heuristic and less than 5% of the responses, in either condition, followed the Linear heuristic. Problem 5 could not be used for this analysis because the predicted values by the proportion and normative model were identical in all of the questions.
3.3 Discussion
Study 1 showed that providing pace data to participants can improve people’s judgments regarding time saved when increasing speed and time lost when decreasing speed. Participants made fewer errors and followed the normative model more often, when they were given pace data compared to when they were not. Although the analysis of non-normative responses was inconclusive, mainly because some of the questions and some of the problems could not differentiate between the competing models adequately enough, it does suggest that pace data mostly affects the rates of responses that follow a linear model (which are the most common non-normative responses when pace data is unavailable) and increase the rates of responses that follow the normative model.
Surprisingly, pace data did not seem to affect the estimations of journey durations in Problem 2: an almost identical percentage of the responses (about 60%) were correct in both conditions. A closer, post-hoc, examination of our data revealed that, in this second problem of estimating the time of a 30 miles journey at various speeds, nine (23%) of the participants in the pace condition gave responses that were actually correct if the journey’s distance would have been 10 miles. In other words, these participants seem to have not noticed that the journey was now 30 miles and, presumably, estimated correctly the duration of a 10 miles journey (as in the previous question). Excluding these participants post-hoc seemed questionable, thus we repeated these questions in Study 2.
In Study 2 we also extended our examination to judgments of the speed required to complete a given journey at various durations. Our hypotheses were that pace data would increase people’s ability to accurately judge a) the duration of a journey at various speeds and b) the speed required to complete a journey at various durations.
4 Study 2
4.1 Method
Sixty-eight AMT workers took part in the study (37 in the pace condition, 31 in the speed condition), which included three problems. Problem 1 was similar to that of Study 1: participants estimated the duration of a 10-mile journey at 20, 40, 50, 55 or 65 mph. In Problems 2 and 3, participants estimated the speed required to complete a journey of 10 miles within 25, 20, 15, 10 or 5 minutes and then the speed required to complete 30 miles within 55, 50, 45, or 40 minutes.
4.2 Results and discussion
We coded and averaged responses as in Study 1 (internal reliability was high: KR-20=.75, .75, .76, for Problems 1—3, respectively). Figure 4 shows the comparison of the percentages of the three types of responses between the pace and speed conditions in the three problems. As Figure 4 shows, in Problem 1 participants in the pace condition estimated journey duration better than participants in the speed condition (90.81% vs. 68.39%). Participants in the pace condition also better estimated the speed required to complete 10 miles (Problem 2, 80.00% vs. 49.29%) and the speed required to complete 30 miles (Problem 3, 38.79% vs. 20.37%). A logistic regression on the propensity to provide correct responses with the condition, questions, and their interaction as independent variables showed a statistically significant effect for the condition in all three problems (Wald χ2(1) = 24.39, 31.62, 8.58, respectively, p < .01). The questions showed a statistically significant effect only in Problem 2 (Wald χ2(1) = 10.49, p < .01). Although the interaction between questions and condition was statistically significant in Problems 1 and 2 (Wald χ2(1) = 5.13, 4.12, respectively, p < .05), the effect of the condition in all questions was in the same direction. These results showed that participants in the pace condition had a significant advantage over those in the speed condition when estimating a journey’s time and the speed required to complete a journey at various speeds.
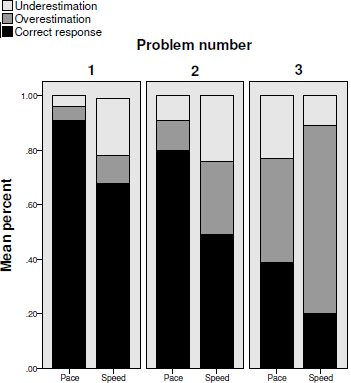
Figure 4: Percent of correct responses, overestimations and underestimations in each of the three problems of Study 2 in the pace and the speed conditions.
We did not analyze the non-normative responses in the study (as we did in Study 1), because this study did not include questions about time-savings, and our models cannot generate predictions regarding estimations of the required speed.
Study 2 extended the results of Study 1 and demonstrated that pace data can also help people estimate the speed required to complete a given journey in a certain time. In Study 3, we replicated Studies 1 and 2 using kph instead of mph in a non-U.S. sample.
5 Study 3
5.1 Method
One hundred and twelve undergraduate students in an Israeli college took part in the study (58 in the pace condition, 54 in the speed condition). The kph versions of the Paceometer and speedometer were used, and all questions were presented in kph. In Problems 1 and 2, participants estimated a 10- and 30-km journey’s duration at speeds of 20, 40, 60, 80, 100 or 120 kph. In Problems 3 and 4, participants estimated the time saved when increasing from 40 kph to 50, 60 or 70 kph for 20 km, and from 100 kph to 110, 120, 130 or 140 kph for 100 km. In Problem 5, participants estimated the speed required to travel 20 and 100 km in exactly 20 or 50 minutes, respectively.
5.2 Results and discussion
We coded and averaged responses as in the previous two studies (internal reliability again was high: KR-20=.91, .81, .84, .69 for Problems 1—4, respectively; the correlation between the two questions of problem 5 was .58, p < .01). Figure 5 shows the comparison of the percentages of the three types of responses between the pace and speed conditions in the three problems. As Figure 5 shows, compared to the speed condition, participants in the pace condition better estimated the duration of a 10-mile journey (91.09% vs. 76.54%), as well as a 30-mile journey (78.45% vs. 64.20%). Participants in the pace condition were also more accurate in estimating time saved when increasing from 40 kph (43.10% vs. 25.31%) and from 100 kph (73.64% vs. 53.57%). Finally, participants in the pace condition also estimated the speed required for completing a journey (86.21% vs. 60.19%) better than participants in the speed condition.
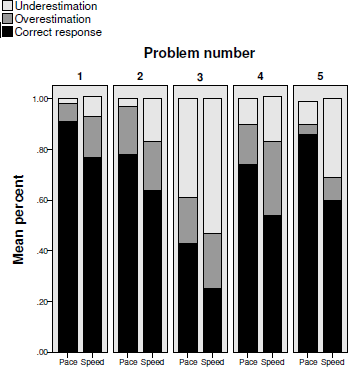
Figure 5: Percent of correct responses, overestimations and underestimations in each of the five problems of Study 3 in the pace and the speed conditions.
A logistic regression on the propensity to provide correct responses in each problem, with the condition, questions, and their interaction as independent variables, showed statistically significant effects for the condition in Problems 1 through 4 (Wald χ2(1) = 25.8, 16.48, 11.54, 12.72, p < .01). The questions and interaction showed a statistically significant effect only on Problem 4 (Wald χ2(1) = 6.35, respectively, p < .05). A logistic regression on each of the two questions in Problem 5 showed a statistically significant effect for the condition in both of the questions (Wald χ2(1) = 35.27, 50.11, respectively, p < .01). These results showed that, as in previous studies, participants in the pace condition had a significant advantage over those in the speed condition when estimating journey times at various speeds, time saved when increasing speed, and the speed required to complete a journey at various speeds.
5.2.1 Non-normative responses
We tested the theoretical models that we used for Study 1 (the normative model, the Proportion heuristic and the Linear heuristic) on the problems of time-savings judgments in this study as well. Problem 3 (estimating time saved when increasing from 40 kph) could not be analyzed because most of the predicted values by the different models were too similar or identical. In Problem 4 we found that, overall, about 52% of the participants’ responses could be classified to one of these models. We found that 56.75% of the responses in the pace condition followed the normative model, compared to only 38.84% in the speed condition. None of the responses in the pace condition followed the Proportion heuristic and less than 2% followed the Linear heuristic. In the speed condition, less than 1% of the responses followed the Proportion heuristic and 4.02% followed the Linear heuristic. It appears that pace data reduced the propensity to follow any of the non-normative heuristics, which were slightly more present in the responses of the speed condition participants. However, since almost half of the responses could not be attributed to any of the models, we do not regard these results as conclusive.
The results of Study 3 replicated the findings of Studies 1 and 2 in a non-U.S. sample, using kph rather than mph. Participants presented with pace data estimated journey times, time savings, and required speed to complete a journey better than participants who received only conventional speed data.
6 General discussion
In Studies 1–3, we showed how pace data improved judgments of driving time and speed. Participants who received pace data estimated journey times at various speeds, time saved (or lost) when increasing (or decreasing) speed as well as the speed required for completing journeys of different durations better than participants who received only conventional speed data. These findings were replicated in both U.S. and non-U.S. samples, using units of mph or kph, respectively: participants who received pace data were considerably, and significantly, more accurate in their judgments than participants who did not receive pace data.
These findings suggest that people can utilize pace data as an effective tool in improving their judgments about driving speed and journey time. Pace data appears to simplify these cognitively complicated tasks in a way that might be analogous to the de-biasing of other cognitive biases. This situation is akin to the aforementioned MPG illusion in which people mistakenly think that a car’s fuel efficiency is linearly related to its MPG (Reference Larrick and SollLarrick & Soll, 2008). Converting data to GPM (gallons per 100 miles) is, essentially, another form of presenting pace data instead of speed. This de-biasing technique appears to work well in various contexts because it provides people with data that is more in line with their intuitive expectations, thereby reducing their biased estimations.
The proposed Paceometer has been found to be effective in improving people’s time and speed judgments. As previously mentioned, the main advantage of the Paceometer is that it simplifies the difficult cognitive task of estimating time saved (or lost) when increasing (or decreasing) speed, as well as the speed required to complete a journey at a given time. In addition to these advantages, the decreasing differences between the pace values on the Paceometer illustrate the curvilinear relationship between increasing speed and reducing journey time: the same increase of 10 mph of speed from a low speed (e.g., from 20 to 30) saves much more time than the same speed increase done from a higher initial speed (e.g., 50 to 60 mph; 10 minutes vs. 2 minutes of time saved per 10 miles, respectively). Thus, we would expect that if drivers were to use this Paceometer on a daily basis, it might “correct” their faulty intuitions on the impact of increasing speed on journey time. Future studies could explore the applicability of using the Paceometer in daily driving situations or examine it’s effects in controlled settings, using driving simulators.
Although the time-saving bias is most easily demonstrated in driving situations, it is not limited to driving only. Other contexts in which people may have biased estimations regarding time-savings are found in many everyday situations. Worker productivity rates are often measured in speed—in typing (words per minute), telemarketing (calls made per hour), sales (products sold per day), and manufacturing (products made per hour). Additionally, some consumer products are often described in terms of their speed. For example, Internet suppliers offer consumers various download rates (megabits per second) and lawnmower producers highlight their product’s speed (acreage mowed per hour). Individuals asked to compare and decide between two speed options may make the same faulty estimations as drivers did in this and previous studies. The time-saving bias predicts that most people would estimate that they would save more time downloading files when they upgrade their Internet speed from 20 to 50 megabits per second rather than from 5 to 10 megabits per second, when actually the latter saves more time. It is possible that converting these speed measures into the appropriate pace data (for example, measuring Internet speed as “seconds per 10 megabits”) would improve people’s judgments in other contexts as well. To illustrate, one can even use the Paceometer introduced in this paper for evaluating Internet speed, simply by using megabits instead of miles and seconds instead of minutes. This way, the Paceometer can show that increasing Internet speed from 5 to 10 megabits per seconds saves 60 seconds per 10 megabits, while increasing speed from 20 to 50 megabits per second only saves 18 seconds per 10 megabits.
In this paper, we tried to highlight a general cognitive phenomenon in which people misestimate time-savings when increasing speed and suggested that this bias is due to the commonly used speed measures that extenuate people’s inability to recognize the curvilinear relationship between these speed measures and the reduction of activity time. We offer a simple remedy for this bias: converting speed values to pace data, which simplifies the cognitive task of judging time-savings because the data conforms to people’s lay perceptions. We believe that this simple solution can be applied to other contexts in which individuals’ judgments might be biased.








