1 Introduction
Tversky and Kahneman’s (Reference Tversky and Kahneman1981) introduction of the Asian Disease Problem was among the earliest examples of the malleability of human decision making. At the heart of this problem is the choice between a riskless option and a risky option of equal expected value. Because the current study will dissect the components of the prototypical risky-choice paradigm as exemplified by the Asian Disease Problem, we now describe these components. The Sure-Thing option offers a fixed (riskless) outcome. In the Positive framing condition it is “save 200 (out of 600) lives” whereas in the Negative condition it is “400 will die.” The Risky option offers a “one-third chance of saving all the lives and a two-thirds chance of saving no lives” in the Positive condition and a “one-third chance that no one will die and a two-thirds chance that all will die” in the Negative condition.
In response to this choice problem, the majority of decision makers choose the riskless or “Sure-Thing” option over the Risky option when potential outcomes are framed as gains (lives saved) but choose the Risky option over the Sure-Thing option when the exact same objective outcomes are framed as losses (deaths). Later attempts to replicate this phenomenon and extend it to other domains such as money gained or lost rather than lives did not always duplicate the literal preference reversal, but a general preference shift of more risky choices to avoid losses than to achieve gains is one of the most solid findings in judgment and decision making research (see reviews by Kühberger, Reference Kühberger1998; Levin et al., Reference Levin, Schneider and Gaeth1998). Later research uncovered task characteristics and individual difference factors that moderated the reliability and magnitude of the risky-choice framing effect (Fagley & Miller, 1997; Highhouse & Paese, 1996: Levin et al., Reference Levin, Gaeth, Schreiber and Lauriola2002; Wang, Reference Wang1996). The present study focuses on one such individual-difference factor.
The aim of the current study is to dissect the risky-choice framing effect into its component parts and to examine the moderating effect of an important individual-difference variable, numeracy, defined as the ability to understand probabilistic and mathematical concepts. We asked participants in each framing condition to judge the full scenario and also to separately judge both the Sure-Thing component and the Risky component. In that way, we can assess the extent to which the Full Scenario framing effect is driven by framing of the separate components, and we can compare this for individuals differing on a variable known to be associated with more superficial vs. more complex processing of numeric information in decisions.
1.1 Numeracy moderates framing effects
Numeracy refers to the ability to understand and use mathematical and probabilistic concepts. Based on the National Adult Literacy Survey, almost half of the general U.S. population has difficulty with relatively simple numeric tasks such as calculating the difference between a regular price and sales price using a calculator or estimating the cost per ounce of a grocery item. These individuals do not necessarily perceive themselves as “at risk” in their lives due to limited skills; however, the research reviewed below demonstrates that having inadequate numeric skills is associated with lower comprehension and use of numeric information in health and financial domains.
Not surprisingly, greater ability with numbers leads to more comprehension of numeric information in important decisions (e.g., mammograms; Schwartz et al., Reference Schwartz, Woloshin and Welch1997). Numeracy relates in somewhat less intuitive ways to a variety of cognitive and affective biases in decision making (Peters et al., Reference Peters, Dieckmann, Västfjäll, Mertz, Slovic and Hibbard2006). For example, Dehaene (Reference Dehaene1997) suggests that, while children spend a lot of time learning the mechanics of math, they may not really understand how to apply those mechanics even in adulthood. We propose that those high in numeracy will be more likely to do so. As a result, they should, for example, find alternative frames of the same number more accessible and more influential in decisions.
Peters et al. (Reference Peters, Dieckmann, Västfjäll, Mertz, Slovic and Hibbard2006) examined numeracy’s effect on framing of a single attribute by presenting participants with the exam scores of five psychology students and asking them to rate the performance of each student on a 7-point scale from –3 (very poor) to +3 (very good). The framing of the exam scores was manipulated as either percent correct or percent incorrect so that “Emily,” for example, was described as having received either 74% correct on her exam or 26% incorrect. In a repeated-measures analysis of variance of the rated performance, the usual framing effect was shown such that the more positive frame elicited more positive ratings. Furthermore, the interaction of numeracy with the frame was also significant, with the less numerate participants showing a stronger framing effect. These findings are consistent with high-numerate participants being more likely to retrieve and use appropriate numerical principles and transform numbers presented in one frame into a different frame, and the less numerate responding more to the affect communicated by the single given frame of the information. We believe that less numerate decision makers are left with information that is less complete and lacks the complexity and richness available to the more numerate. Controlling for a proxy measure of intelligence (self-reported SAT scores) did not alter the results. Actual number ability appears to matter to judgments and decisions in important ways not captured by other measures of achievement or ability.
Although Peters et al. (Reference Peters, Dieckmann, Västfjäll, Mertz, Slovic and Hibbard2006) did not examine risky-choice frames, an unpublished Master’s Thesis by Garcia (Reference Garcia2006, supervised by Peters), using a risky-choice paradigm, found no effect of numeracy on risky-choice framing problems. We were curious about this lack of finding given the robust nature of numeracy’s influence on attribute framing, and our speculation that risky choices in such problems were based on evaluations of the two options comprising the choice: the Sure-Thing option and the Risky option. In prior studies of numeracy, highly numerate individuals have demonstrated deeper processing of numeric information by showing smaller framing effects (presumably caused by transforming the given numeric frame to its normative equivalent) and by being more likely to draw meaning from number comparisons in judgments (Peters et al., Reference Peters, Dieckmann, Västfjäll, Mertz, Slovic and Hibbard2006). The highly numerate appeared to integrate more sources of information than the less numerate. In a separate study, the highly numerate were more likely to be sensitive to numeric information in judgments of the attractiveness of a hospital whereas the less numerate were insensitive to provided numeric information and appeared to misattribute their current mood to the judgment instead (Peters et al., under review). Thus, it was curious in Garcia (Reference Garcia2006) that numeracy did not influence risky-choice framing effects in a similar manner with greater effects of the provided frame on the less numerate. However, as pointed out by Levin et al. (Reference Levin, Schneider and Gaeth1998), the risky-choice framing paradigm is more complex than the attribute-framing paradigm which has been the source of previous work on the influence of numeracy. In attribute framing, a single attribute of an object is alternatively labeled in positive or negative terms (e.g., success rate versus failure rate of a medical treatment) and its effect on the evaluation of that object is assessed. No manipulation of risk is involved. In risky-choice framing, the labeling of outcomes is manipulated and the element of risk is added by creating choice options of varying risk level.
We developed the following hypotheses:
-
1. In order to replicate the basic Risky-Choice Framing effect, we expect that the Risky option will be preferred more than the Sure-Thing option in the negative framing condition than in the positive framing condition.
-
2. Based on Garcia’s (Reference Garcia2006) findings, individuals high and low in numeracy will demonstrate similar framing effects in risky choices.
-
3. Because the Sure-Thing option is similar to an attribute-framing problem (i.e., a single attribute is manipulated such as “400 of 600 lives will be lost”), we expect the frame to influence evaluations of the Sure-Thing option more for the less numerate than the highly numerate.
-
4. Because the less numerate appear to integrate fewer pieces of information and to respond more than the highly numerate to non numeric sources of information such as mood states, they would be expected to focus on a single favorable statement such as the sure gain provided by the Sure-Thing option in the Positive frame or the possibility of no loss provided by the Risky option in the Negative frame. By contrast, the highly numerate who use numeric information more completely are expected to be more capable of integrating all the information from both options in their choices. Thus, choices of the highly numerate should be more influenced by their evaluations of the separate options.
2 Method
2.1 Participants
Participants were 108 students (42% female) fulfilling a research participation component of an introductory marketing course at the University of Iowa.
2.2 Design
Participants were randomly assigned to a Positive frame group (N = 53) or a Negative frame group (N = 55).Footnote 1 Within each group, participants rated their degree of preference between the options in the Full Scenario task and then provided separate ratings of the attractiveness of the Sure-Thing and Risky options. They did this for each of five scenarios. Further procedural variations are described below.
2.3 Materials
Five scenarios were constructed, each patterned after the Asian Disease Problem but different in content domain and in the expected value of the options. The Positive and Negative frame versions of the scenarios are reproduced in Appendix A. Briefly, one is an exact replication of the Asian Disease Problem except that it was simply called an “unusual disease” from Sweden, one involves animals endangered by wildfires, one involves crop destruction from a severe drought in another country, one involves loss of medical benefits in another country, and one involves investment losses. The introduction to the full scenario was repeated each time a response was required for either the full risky-choice problem or one of its components.
2.4 Procedure
Participants rated the five Full Scenarios, the five Sure-Thing options in two formats, and the five Risky options in two formats, each presented in separate blocks in their booklet to ensure that the separate ratings for each part of the same scenario were spaced far enough apart to reduce memory effects. Participants made four other responses (the other four scenarios) before revisiting the same scenario. Each response took about one minute. Furthermore, the response scales were varied between the full risky-choice problem and the components.
Each participant received the same frame throughout the experiment. The Full Scenarios were always presented first. Participants were not allowed to look back at earlier responses. Each participant then responded to both the Sure-Thing and Risky options in two separate formats in different blocks of trials. The Sure-Thing option was presented in one block as a numerical count (e.g., 200 people will be saved) and in another block as a fraction (1/3 of the 600 people will be saved) in order to examine whether different effects of frame were produced; the Risky option was presented once with the better outcome (e.g., 1/3 chance of saving all lives) first and again with the worse option (2/3 chance of saving no lives) presented first. Four different orders of presentation of these four blocks were constructed and counterbalanced across participants.
In the Full Scenario, participants were asked to check one of seven boxes labeled from “Much prefer A” (the Sure-Thing option) to “Much prefer B” (the Risky option) with a midpoint of “A and B are equal.” This expansion of the usual dichotomous choice was done in order to provide continuous numerical data for the statistical (regression) analyses (see Levin et al., Reference Levin, Gaeth, Schreiber and Lauriola2002). Responses were scored such that higher numbers represent greater preferences for the Risky option.
To evaluate the Sure-Thing option and the Risky option separately, participants were asked to circle a number between –3 (Very bad) and +3 (Very good) with a midpoint of 0 (Neither bad nor good) to indicate their evaluation of that particular option.
2.5 Individual difference measures
After completing the ratings tasks, participants were asked to complete the following: a demographic information sheet including age, gender, GPA, and ACT scores; the 18-item Need for Cognition scale (Cacioppo et al., Reference Cacioppo, Petty and Kao1984); and the 11-item Numeracy scale shown in Appendix B (Lipkus et al., Reference Lipkus, Samsa and Rimer2001).Footnote 2
All inferential statistics used mean-deviated continuous scores (Irwin & McClelland, Reference Irwin and McClelland2001). A median split on numeracy was used for descriptive statistics and to identify low and high scorers so that inferential analyses could be conducted separately within each group.
3 Results
In contrast to some previous studies, men and women scored about the same on numeracy (scores = 9.5 and 9.2, respectively, t(106) = 1.0, p = .32). Higher numeracy was associated with higher self-reported GPA and higher ACT scores (r = .16, p < .10 and .28, p < .01). Numeracy and Need for Cognition were not significantly related (r = .10, ns).
3.1 Analysis of the dual formats for the sure-thing and risky options
We first examined whether the two formats of the Sure-Thing options (counts versus proportions) and, separately, of the Risky option (the two orders) produced different framing effects on evaluations. A repeated-measures analysis of variance (repeated-measures ANOVA) was conducted of the attractiveness ratings for the Sure-Thing options in the five scenarios with format, frame, numeracy (continuous, mean-deviated), and their interactions as predictors. A similar analysis was conducted of attractiveness ratings of the Risky options. Format did not significantly influence the attractiveness ratings as a main effect or in interaction with frame or numeracy for either the Sure-Thing or Risky options.
Correlations between responses to the two formats were similar for the low and high numerate (average r = .58 and .60 between the two Sure-Thing formats, respectively, for individuals low and high in numeracy across the five scenarios and average r=.41 and .53, respectively, between the two Risky formats). This consistency might be considered puzzling from the standpoint that individuals lower in numeracy presumably have more difficulty using numbers in judgments and decisions and therefore should perhaps be less consistent. The consistency is not puzzling, however, from the standpoint that the less numerate may process different information than the highly numerate, with the less numerate processing numeric information more superficially. Our expectation is that the less numerate will respond more to the given frame of information (which was the same across the formats for a given participant) rather than the numbers. We retained only the usual formats (the count format for the Sure-Thing option and the better outcome first for the Risky option) in further analyses.
3.2 Separate analyses of Full Scenarios and components
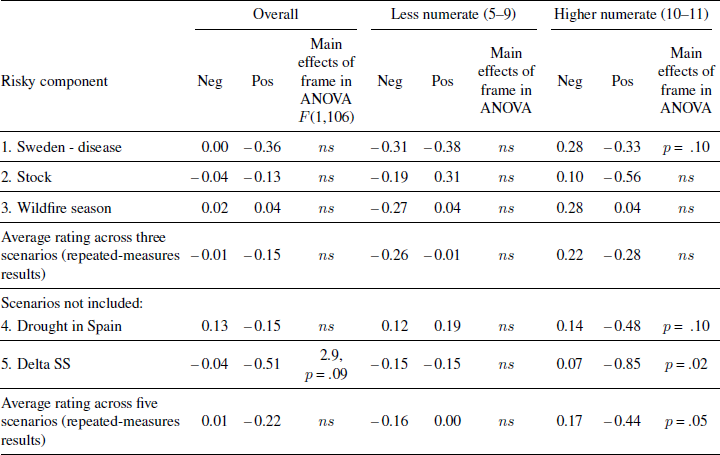
We next examined the Full Scenarios to test for the usual risky-choice framing effect and to verify that numeracy again did not moderate the effects of framing at this level. A repeated-measures ANOVA of choice preferences was conducted with the five problems as the repeated measures and frame (–1, 1), numeracy (continuous and mean-deviated), and their interactions as the predictors. Consistent with Hypothesis 1, an overall effect of frame was found, F(1, 104) = 18.9, p < .001, with individuals preferring the sure-thing option in the domain of gains — the positive frame — and the risky option in the domain of losses — the negative frame (average choice preferences = 3.51 and 4.31, respectively, where a response of 4 indicates no preference between the two options and lower numbers indicate a preference for the sure option). Numeracy and its interaction with frame were non-significant (F(1, 104) = .04, p = .85 and F(1, 104) = 1.8, p = .28, respectively). The effects of frame differed by scenario, F(4, 416) = 2.9, p < .05, with framing effects being nonsignificant in the scenarios in which the risky option had a higher expected value than the sure-thing option (the Spanish drought and Delta’s medical-benefit crisis). In the positive frame of both scenarios (where decision makers are generally risk-averse), preferences for the risky option were noticeably stronger for both high- and low-numerate participants. See Table 1 for preference means by frame and numeracy.
As a result of this initial analysis, we dropped the two non-significant framing problems and focused further data analysis on the three scenarios that showed significant effects of frame on risky choices (but see the tables for results with the two dropped scenarios). A repeated-measures ANOVA of those three scenarios revealed a stronger overall effect of frame, F(1, 104) = 30.5, p < .001, with average choice preferences of 3.0 and 4.2, in the positive and negative frames, respectively. In this analysis, the main effect of numeracy remained nonsignificant, but the highly numerate demonstrated a marginal tendency towards smaller framing effects than the less numerate, F(1, 104) = 3.3, p = .07.
Table 1: Preference means by frame and numeracy

Note: Higher numbers represent greater preference for the risky option.
N = 108; n = 52 and 56 for less and higher numerate, respectively.
As suggested in Hypothesis 2, the effects of frame by numeracy were not conventionally significant in the risky-choice frame (the Full-Scenario decision), and the effects of frame were significant in separate analyses of low and high numerate groups. Previous studies, however, have shown that more and less numerate decision makers appear to use different sources of information in decisions, setting the stage for our hypotheses concerning different information-processing mechanisms underlying risky-choice framing effects for those low and high in numeracy. Thus, we turn to an analysis of framing in evaluations of the separate options next.
A repeated-measures ANOVA was conducted of the attractiveness ratings of the remaining three Sure-Thing options with frame, numeracy (mean-deviated and continuous) and their interaction as predictors. Previous research has demonstrated that individuals lower in numeracy show stronger attribute-framing effects than those higher in numeracy. As stated in Hypothesis 3, we expected that ratings of the Sure-Thing option would be similar to an attribute frame. The overall effect of frame was significant with Sure-Thing options in the positive frame rated as more attractive than those in the negative frame (attractiveness means = .53 and –.28, respectively, F(1, 104) = 10.8, p < .01). As hypothesized, less numerate individuals showed stronger framing effects than did the highly numerate, interaction F(1, 104) = 3.9, p = .05.
Examination of the means by frame separately within low and high numerate groups (based on a median split, the highly numerate scored 10 or 11 correct out of 11 possible, whereas the low-numerate group scored between 5 and 9 correctFootnote 3) revealed a significant framing effect among the less numerate (attractiveness means in the positive and negative frame were .73 and -.54, respectively, p < .001) and a non-significant effect for the highly numerate (means = .35 and –.05, respectively, ns). In no case was the framing effect for a scenario greater for the highly numerate than for the less numerate. See Table 2 for attractiveness means by frame and numeracy.
Table 2: Attractiveness means of the Sure-Thing options by frame and numeracy

We conducted a similar repeated-measures ANOVA with attractiveness ratings of the Risky option. In this case, we were not sure what to expect because two diametrically opposite effects are theoretically possible. First, negative frames could lead to the gamble being perceived as more attractive, consistent with Prospect Theory’s psychological shift towards risk seeking in this frame compared to the positive frame. Second, negative frames could lead to poorer evaluations of the gamble compared to positive frames, consistent with an attribute-framing effect. Results of the analysis demonstrated no overall effects of frame or its interaction with numeracy. However, an analysis by scenario shown in Table 3 indicated a nonsignificant tendency for the highly numerate to rate the attractiveness of the Risky component as higher in the negative frame than the positive frame condition in every scenario, whereas the less numerate tended to show the opposite pattern. This pattern was significant for the highly numerate when all five scenarios were considered.
Table 3: Attractiveness means of the Risky options by frame and numeracy
3.3 Full-Scenario risky-choice framing effects as a function of evaluations of the separate options
Thus far, we have found different effects of frame for the more and less numerate in evaluations of the separate options. This result may explain the overall lack of effect of numeracy on risky-choice framing. Specifically, the less numerate showed stronger framing effects in their evaluations of the Sure-Thing option; the highly numerate were not influenced by frame in their evaluations of the Sure-Thing option but appeared to be somewhat influenced by a framing effect consistent with Prospect Theory in their evaluations of the Risky option. Thus, we turn to an examination of the extent to which the frame, the evaluations of both options, and their interactions with numeracy influenced the full risky-choice framing effect. Hypothesis 4 stated that the frame would have a direct influence on choice preferences of the less numerate with little influence from their evaluations of the separate options, suggesting a more superficial reaction to the verbal cues identifying the positive and negative frames. For the highly numerate, however, we expected that the separate evaluations of the Sure-Thing and Risky options would guide their choice preferences, indicating their more analytical, componential approach to decisions involving numeric information.
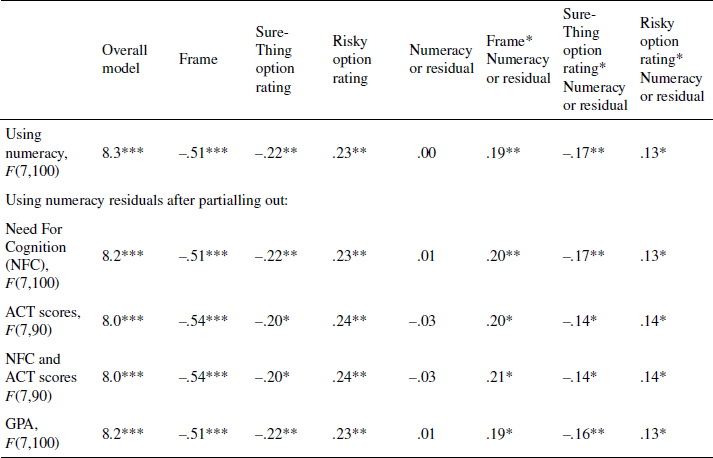
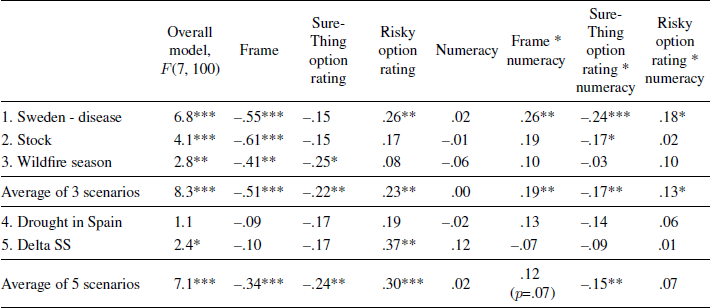
To simplify this analysis, we constructed average ratings across the three problems for evaluations of the Sure-Thing option and the Risky option, as well as average choice preferences for the Full-Scenario risky choices. A regression analysis was conducted of the average choice preference in the Full-Scenario risky choices; independent variables were the direct effects of frame, the average mean-deviated Sure-Thing attractiveness rating, the average mean-deviated Risky attractiveness rating, numeracy (mean-deviated and continuous), and the three two-way interactions with numeracy (model F(7, 100) = 8.3, p < .001, R-squared = .37). Although the frame was associated with the component ratings, correlations among the predictors were small enough that multicollinearity did not appear to be a problem (the tolerances were acceptable; range = .72-.96).
The results indicated a main effect of frame such that individuals in the positive-frame condition tended to prefer the Sure-Thing option more than those in the negative-frame condition (b = –.51, t(100) = –4.9, p < .001). In addition, individuals who rated the Sure-Thing option as more attractive were more likely to prefer it (b = –.22, t(100) = –2.6, p = .01) and those who rated the Risky option as more attractive were more likely to prefer the Risky option (b = .23, t(100) = 2.7, p < .01). Numeracy did not have a direct influence on risky-choice preferences. However, the main effects were qualified by three interactions. Individuals lower in numeracy were influenced more than those higher in numeracy by the frame in the risky-choice scenarios (interaction b = .19, t(100) = 2.6, p = .01). Choice preferences of individuals high in numeracy were influenced more than those low in numeracy by the attractiveness of the Sure-Thing option as well as the Risky option (interaction b = –.17, t(100) = –3.1, p < .01 and b = .13, t(100) = 2.1, p < .05, respectively). A similar pattern of results was shown in each of the three scenarios with strongest effects in the Swedish disease problem (see Table 4).
Table 4: Regression results (b-values) predicting the Full-Scenario risky-choice preferences by scenario, on average across the three scenarios, and on average across the five scenarios
Note:
* p < .05;
** p < .01;
*** p < .001.
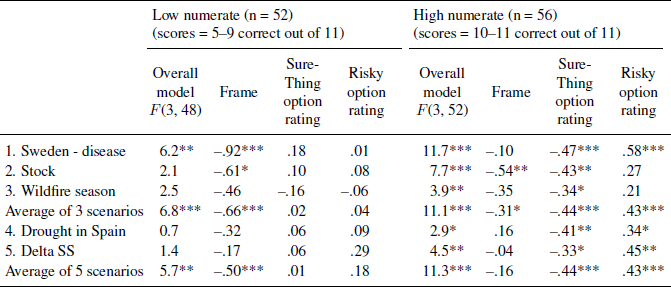
In order to examine these numeracy interactions in more detail, a median split was performed on numeracy. Regression analyses of the average choice preference were conducted with frame, the average Sure-Thing attractiveness rating, and the average Risky attractiveness rating as predictor variables, separately within each median split of numeracy (see Table 5 for detailed results). For individuals high in numeracy, the model strongly predicted their preferences (model F(3, 52) = 11.1, p < .001, R-squared = .39). Frame was the smallest influence on their preferences compared to the ratings of the separate options; the average attractiveness ratings of the Sure-Thing and Risky options were both highly predictive. Among the less numerate, the model was less predictive of their preferences but still highly significant (model F(3, 48) = 6.8, p < .001, R-squared = .30). Frame was the strongest predictor by far of their preferences; average attractiveness ratings of the Sure-Thing and Risky options did not predict their choice preferences.
Table 5: Regression results (b-values) predicting the risky-choice preferences in low and high numeracy groups
Note:
* p < .05;
** p < .01;
*** p < .001.
We partialled out the effects of ACT scores and Need For Cognition (NFC) from numeracy scores using regression and then used the resulting numeracy residuals to conduct again the analyses of the Full-Scenario risky-choice problems above. The results did not change in any substantial way. A second analysis, after partialling out the effects of GPA from numeracy instead, also showed no substantial changes from the original analysis. Numeracy appears to influence framing effects over and above these proxy measures of intelligence and preference for thinking harder (see Appendix C for more detailed results). A similar set of analyses was conducted using NFC scores in place of numeracy (with and without partialling out the effects of numeracy, ACT scores, and GFA). Neither NFC nor its interactions with frame or ratings of the component options significantly predicted choices in any analysis.
Another way to examine the extent to which participants were consistent in their evaluations is to compare the inferred choice preference calculated from the attractiveness ratings of the separate options and the actual choice preference made when the two options were presented jointly. To do this, for each pair of ratings, we subtracted the rating for the Sure-Thing option from the rating for the Risky option. Thus, higher values meant greater inferred preference for the Risky option over the Sure-Thing option, just as it does for the actual choice preference. Correlations by scenario were then calculated between the choices inferred from these differences and the actual choice responses, separately within the low- and high-numerate groups. Finally, the average correlation (computed across the five scenarios) was calculated within each group.
The results demonstrated greater consistency of inferred and actual preferences among the high numerate than among the less numerate. Specifically, the average correlation between inferred and actual choice preferences across the five scenarios was .45 and .09 for the high and low numerate, respectively (the respective ranges of correlations were .36 to .63 and .01 to .15).Footnote 4
4 Discussion
These results help us understand both the risky-choice framing phenomenon and the role of numeracy in decision making. Risky-choice framing effects appear robust (with the highly numerate demonstrating a tendency towards a smaller effect of frame compared to the less numerate). These effects, however, do not appear to be a singular effect as previously thought, but rather have different underlying mechanisms for different people.
In particular, in analyses of the less numerate, they demonstrated a direct effect of frame on their choices and no significant effects of how attractive they found the separate options. This lack of influence may be due to the less numerate attending more superficially to the individual options and attempting less to evaluate them; they may focus, for example, on the sure gain in the Sure-Thing option when choosing in the positive frame and the possibility of no loss provided by the Risky option in the negative frame. It may also be, however, that the less numerate are less able to translate information about a given option into an attractiveness rating. If this is the case, then the ratings of the less numerate should be less reliable (more variable) than those of the highly numerate. There was some evidence consistent with this hypothesis, with the standard deviation of responses to the five Sure-Thing components, five Risky components, and five Full scenarios being higher for the less numerate compared to the highly numerate in 11 of the 15 responses (p = .059, based on a sign test using the binomial distribution), but the size of the difference was small with standard deviations of responses ranging from 1.38 to 1.75 for the less numerate and 1.32 to 1.68 for the highly numerate. Finally, the less numerate may attend to the individual-option information in the risky choice and may translate it appropriately, but fail to integrate the information in their choices, suggesting that choices are not always based on integrating judgments of provided options. This suggestion is supported by the lower observed consistency among the less numerate between inferred preferences based on component ratings and actual preferences.
The less numerate also demonstrated a larger framing effect on their evaluations of the Sure-Thing options. These results are consistent with previous numeracy results with attribute framing (Peters et al., 2006). In the analysis of the Full-Scenario framing effect, these Sure-Thing evaluations influenced their choice preferences less relative to the preferences of those higher in numeracy. At face value, this result was somewhat inconsistent with the robust numeracy effect in attribute-framing studies; it was, however, consistent overall with Peters et al.’s (Reference Peters2006) interpretation of their attribute-framing results. Specifically, they argued that the less numerate respond more to the given frame of information whereas the highly numerate demonstrated more complex processing of the same information.
Consistent with this argument, the model was more predictive of preferences of the highly numerate than the less numerate. The highly numerate showed only a small direct effect of frame over and above their evaluations of the individual options. Evaluations of both options influenced their choice preferences as if the highly numerate were able to keep on-line both pieces of information during the choice process whereas the less numerate may not be able to keep as much numeric information on-line; pilot data suggest that the highly numerate have somewhat greater working-memory capacity compared to the less numerate (Peters, Reference Peters2006) which could exacerbate this effect. Overall, the highly numerate nonetheless appear to consider both the possibility of ensuring some saving of lives (their evaluations of sure-thing options) and the possibility of avoiding loss of life (evaluations of risky options). One caveat on this argument is the correlational nature of the design combined with all participants responding to the Full Scenarios first and the component options second. Given this, it is possible that participants simply attempted to be consistent from the first choice response to the later attractiveness ratings, and the highly numerate were more successful at this consistency. Further studies should explore both these working-memory and order issues.
These results provide additional evidence that the highly numerate not only understand numbers better, as shown in past studies, but they use them more frequently as well. This is important for two reasons. First, it again highlights the distinction between comprehension and use of information. Decision makers all may know that 200 is one-third of 600, but bringing this information (e.g., evaluations of the Sure-Thing option) to bear on decisions is another matter. Compared to the less numerate, the highly numerate appeared to use more complex processing of given numeric information in the construction of their preferences. Second, the results are a reminder that information providers can, and perhaps should, provide additional assistance to decision makers by paying careful attention to how numeric information is provided in order to help the less numerate make better use of numerical information (e.g., Fagerlin et al., Reference Fagerlin, Ubel, Smith and Zikmund-Fisher2007). Testing formats may be critical, as the intuitions of information providers concerning best ways to present information may not be adequate. As Fischhoff (in press) argued, “One should no more release untested communications than untested pharmaceuticals.”
These results demonstrate that the well-known risky-choice framing effect is more than one effect. Debiasing these effects, therefore, may require different methods for different people. For the less numerate, providing numeric information in formats that are easier to evaluate (and allow them access into the meaning of the information that can then be used in decisions; Peters et al., Reference Peters, Hibbard, Slovic and Dieckmann2007) may be best. The highly numerate may already access the meaning of the information, and debiasing may involve encouragement to think harder about the individual options.
At a broader level, we feel that the paradigm introduced here can be applied to other phenomena in human judgment and decision making. In a number of choice situations with options varying on dimensions such as complexity, there are opposing models for the decision-making process that pit an algebraic comparison of the integrated values of the choice options against a heuristic solution based on which option “feels” better. For example, performance on ambiguity-probability tradeoff tasks originating with Ellsberg’s (1961) two-color problem has been explained as either a process where the unknown probability for an ambiguous option is estimated and then compared to the known probability of the unambiguous option or as a process where the option with the most information is preferred (see Lauriola et al., Reference Lauriola, Levin and Hart2007). By having each respondent rate both ambiguous and unambiguous options separately as well as making a forced choice, and by including individual-difference measures such as those used by Lauriola et al., comparisons can be made between those individuals who are more apt to be influenced by component evaluations and those who are more apt to use simplifying heuristics in forced-choice situations. As another example, the well-known “decoy” or “asymmetric dominance effect” in consumer behavior involves a change in preference between two options when a third option is introduced which is inferior to one option on all attributes but is superior to the other option on one attribute. The result is an increase in preference for the dominating option (Reference Huber, Payne and PutoHuber et al., 1982). Using the present approach to unravel the processes used by different consumers, respondents would rate each of the separate options as well as make both the two-option choice and the three-option choice. In other words, the approach described in the current paper can be used to categorize individuals in terms of whether choices are based on the separate evaluations of choice options or whether new, usually simplifying, factors emerge in head-to-head forced choices.
Appendix A. Risky-choice scenarios
Positive frames
Options have equal expected value:
1. Sweden is preparing for the outbreak of an unusual disease, which is expected to kill 600 people. The following alternative programs have been proposed to limit the spreading of the disease: If Program A is adopted, 200 people will be saved. If Program B is adopted, there is a 1/3 probability that 600 people will be saved, and a 2/3 probability that no people will be saved.
2. Suppose that you have invested $60,000 in the stock of a company that just filed for bankruptcy. They have proposed two alternatives in order to save some of the invested money: If Program A is adopted, $20,000 will be saved. If Program B is adopted, there is a 1/3 probability that $60,000 will be saved, and a 2/3 probability that no money will be saved.
Sure-thing option A has a higher expected value than risky option B:
3. The wildfire season is about to start and an old growth forest in the Northwest of the US will be affected. This forest is home to 3,600 animals that are endangered by the fire. Two programs have been proposed to protect the animals. If Program A is adopted, 1,560 animals will be saved. If Program B is adopted, there is a 1/3 probability that 3,600 animals will be saved, and a 2/3 probability that none will be saved.
Risky option B has a higher expected value than sure-thing option A:
4. A severe drought is foreseen to hit the South of Spain this summer. The drought will cause the destruction of 24,000 acres of crops. Two programs of water supply have been proposed: If Program A is adopted, 5,600 acres of crops will be saved. If Program B is adopted, there is a 1/3 probability that 24,000 acres of crops will be saved, and a 2/3 probability that none will be saved.
5. The country of Delta’s Social Security System is undergoing a crisis. Economists believe that 12 million seniors will lose their medical benefits next year. Two alternative programs have been proposed to mitigate this problem. If Program A is adopted, 2.8 million senior citizens will keep their medical benefits. If Program B is adopted, there is a 1/3 probability that 12 million seniors will keep their medical benefits, and a 2/3 probability that no senior citizens will keep their medical benefits.
Negative frames
Options have equal expected value:
1. Sweden is preparing for the outbreak of an unusual disease, which is expected to kill 600 people. The following alternative programs have been proposed to limit the spreading of the disease: If Program A is adopted, 400 people will die. If Program B is adopted, there is a 1/3 probability that nobody will die, and a 2/3 probability that 600 people will die.
2. Suppose that you have invested $60,000 in the stock of a company that just filed for bankruptcy. They have proposed two alternatives in order to save some of the invested money: If Program A is adopted, $40,000 will be lost. If Program B is adopted, there is a 1/3 probability that no money will be lost, and a 2/3 probability that $60,000 will be lost.
Sure-thing option A has a higher expected value than risky option B:
3. The wildfire season is about to start and an old growth forest in the Northwest of the US will be affected. This forest is home to 3,600 animals that are endangered by the fire. Two programs have been proposed to protect the animals. If Program A is adopted, 2,040 animals will perish. If Program B is adopted, there is a 1/3 probability that no animals will perish, and a 2/3 probability that 3,600 animals will perish.
Risky option B has a higher expected value than sure-thing option A:
4. A severe drought is foreseen to hit the South of Spain this summer. The drought will cause the destruction of 24,000 acres of crops. Two programs of water supply have been proposed: If Program A is adopted, 18,400 acres of crops will be lost. If Program B is adopted, there is a 1/3 probability that no crops will be lost, and a 2/3 probability that 24,000 acres of crops will be lost.
5. The country of Delta’s Social Security System is undergoing a crisis. Economists believe that 12 million seniors will lose their medical benefits next year. Two alternative programs have been proposed to mitigate this problem. If Program A is adopted, 9.2 million senior citizens will lose their medical benefits. If Program B is adopted, there is a 1/3 probability that zero senior citizens will lose their medical benefits, and a 2/3 probability that 12 million senior citizens will lose their medical benefits.
Appendix B. Numeracy items (Lipkus, Samsa, & Rimer, 2001) with percent correct per item in this sample

Appendix C. Regression results (b-values) predicting the average risky-choice preference across the three scenarios using numeracy and numeracy residuals