1 Recalibration
There has long been interest in bridging the gap between the subjective and objective interpretations of probability. The subjective view, championed by Reference DeFinetti, Kyburg and SmoklerDeFinetti (1937/1964) and Reference SavageSavage (1954), takes statements of probability to indicate the beliefs of the person providing them, as would be reflected in their willingness to bet on fair gambles using those values. The objective view holds that probability is a function of the external world and, hence, that a subjective (or personal) probability can be wrong in some objective sense.
Both views agree, however, on the following laws of probability:
-
(i) for all events A, P{A}≥ 0
-
(ii) if S is the sure event, P{S} = 1
-
(iii) if A and B are disjoint events (i.e., they can’t both happen), then

where
 is the event that
either A or B occurs. If
P assigns numbers to events in such a way that
these assumptions are satisfied, P is said to be
coherent.
is the event that
either A or B occurs. If
P assigns numbers to events in such a way that
these assumptions are satisfied, P is said to be
coherent.
One point of intersection of subjective and objective views is in studies of calibration. As expressed by Reference Lichtenstein, Fischhoff, Phillips, Kahneman, Slovic and TverskyLichtenstein, Fischhoff and Phillips (1982, p. 307), “A judge is calibrated if, over the long run, for all propositions assigned a given probability, the proportion that is true equals the probability assigned. Judges’ calibration can be empirically evaluated by observing their probability assessments, verifying the associated propositions, and then observing the proportion true in each response category.”
They go on to propose that “calibration may be reported by a calibration curve. Such a curve is derived as follows:
-
1. Collect many probability assessments for items whose correct answer is known or will shortly be known to the experimenter.
-
2. Group similar assessments, usually within ranges (e.g. all assessments between .60 and .69 are placed in the same category).
-
3. Within each category, compute the proportion correct (i.e. the proportion of items for which the proposition is true or the alternative is correct).
-
4. For each category, plot the mean response (on the abscissa) against the proportion correct (on the ordinate).”
Empirical studies typically find that the calibration curve deviates, often substantially, from the identity line. In such studies, the subjective probability judgments are evaluated by an objective standard, the observed proportions of correct answers. (For research into the behavioral and measurement properties of these curves, see Reference O’Hagan, Buck, Daneshkhah and EiserO’Hagan, Buck, Daneshkhah, Eiser, et al. 2006; Reference Brenner, Griffin and KoehlerBrenner, Griffin & Koehler, 2005; Reference Budescu and JohnsonBudescu & Johnson, 2011; and the articles in the special issue of the Journal of Behavioral Decision Making [Reference Budescu, Erev and WallstenBudescu, Erev & Wallsten, 1997].) Observing such miscalibration, a natural reaction is to propose a global recalibration of such probability judgments to more accurate ones. According to this logic, if I know my calibration curve, f, and I was about to give p as my probability of an event, I should instead give my recalibrated probability f(p), adjusting for the expected miscalibration. This suggestion runs into a fundamental mathematical difficulty:
Proposition 1
-
a) Suppose recalibration depends only on the subjective probability of the event. That is, every event judged before recalibration to have probability p is recalibrated to f(p). Suppose, in addition, the following are true:
-
b) the subjective probabilities obey the rules of probability given above
-
c) the recalibrated probabilities obey the rules of probability
-
d) there are n exhaustive and mutually exclusive events I regard as equally likely.
Then
Proof of Proposition 1:
By a) I assign equal probability to the events in d), namely 1/n. Recalibrated, I assign f(1/n) to each. Because of c), I must have
i.e.
![]() .
.
Now consider an event that is the union of k ≤
n of the original events. By b), I assign this
event probability k/n. Recalibrated, it now has
probability ![]() . But by c), using
(2), I have that
. But by c), using
(2), I have that
□
Proposition 2:
Suppose e) that I regard some random variable X as having a continuous distribution. Then for every positive integer n, there are events satisfying d) above. Proof of Proposition 2:
Let the cumulative distribution function of X be F. Choose n ≥ 2. Let
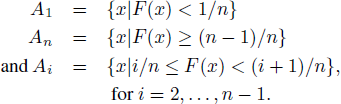
By construction, the sets A i are disjoint (meaning that an x can be in only one), exhaustive (meaning that every x is in one of them), and have (uncalibrated) probability
□
Corollary: If e) holds and if assumptions a), b), and c) of Proposition 1 hold, then
Proof:
Under e), Proposition 1 shows that assumption d) of Proposition 1 holds for all n ≥ 1. The conclusion then follows from Proposition 1. □
Equation (6) shows that under these assumptions, the only possible recalibration curve f is the identity function from the rational numbers to the rational numbers in [0,1].
To explain the import of the conclusion of the corollary, note that:
-
(i) The identity function is a function such that for each value of the input, the output equals the input.
-
(ii) The consequence of the corollary is that the only calibration curve that satisfies assumptions a), b), c) and e) is a straight line from (0,0) to (1,1).
Thus, assuming e) holds, if recalibration depends only on the number originally assigned to the event and if the original judgment and the recalibrated one both satisfy the laws of probability, then they are also the same, meaning that no recalibration can occur. Preliminary versions of this result are given in Reference Kadane and LichtensteinKadane and Lichtenstein (1982), Reference SeidenfeldSeidenfeld (1985) and Reference Garthwaite, Kadane and O’HaganGarthwaite, Kadane and O’Hagen (2005).
There are four assumptions for this result. The first is that recalibration depends only on the probability assigned. It would not hold say for a weather forecaster who over-predicts rain and, hence, under-predicts not-rain. In such cases, knowing the event (rain or not-rain) may allow recalibration. For example, a forecaster might give rain on a particular day a probability of 80% and, hence, not-rain a probability of 20%. Recalibrating these as 70% and 30% might yield more useful forecasts. What cannot be done, according to the Proposition, is to recalibrate every event given probability 80% to be probability 70%. Similarly, an overconfident person might propose an interquartile range that is characteristically too narrow. This means that the overconfident person assigns 25 th and 75 th percentiles to some unknown quantity that are too close to each other. Then the set outside that range would be characteristically too broad, but both sets would have subjective probability 1/2. Both the over-prediction of rain and the over-confident, too-narrow interquartile range are barred by assumption a).
A second assumption, c) above, is that the recalibration results in assessments that obey the laws of probability. Because the recalibrated probabilities are frequencies, this must be the case. The role of assumption d) is to ensure that there are enough events to work with. Proposition 2 is one way to ensure this. A second is to imagine decomposing large lumps of probability into smaller units. For example, an event of probability .2 could be thought of as 1 out of five equally likely events, but it can also be thought of as 200 of 1000 equally likely events. Proposition 2 applies if I am willing to agree to some random variable having a normal distribution, or a uniform distribution, or a chi-square distribution, or any other continuous distribution imaginable. Hence, attention must be focused on the fourth assumption, b) above, examined in the next section.
2 Discussion of assumption b)
Probability judgments can be miscalibrated when individuals have coherent, but misinformed beliefs. In such cases (as just shown), their judgments cannot be recalibrated and still be probabilities. Recalibration might, however, be possible if the flawed judgments were not, in fact, probabilities, but just numeric responses elicited on probability-like scales. Knowing whether judgments are probabilities requires evaluating their internal consistency (or coherence). Such tests are, however, rare in calibration studies. When consistency checks are performed, they are typically modest, conducted with the hope of getting a hearing from skeptics poised to dismiss any numeric expression of uncertainty (e.g. Bruine de Reference Bruine de Bruin, Fischhoff, Brilliant and CarusoBruin, Fischhoff, Brilliant & Caruso, 2006; Reference Fischhoff, Parker, Bruine de Bruin, Downs, Palmgren, Dawes and ManskiFischhoff, Parker, Bruine de Bruin, Downs, Palmgren, Dawes & Manski, 2000).
Those numeric judgments might be made more useful by recalibration, so that “when someone says X%, treat it as Y%.” Unfortunately for such simple solutions, experimental psychologists have long known that translating internal states into observable behavior involves complex psychological processes, subject to sometimes subtle details of how judgments are elicited (e.g., Reference Woodworth and SchlosbergWoodworth & Schlosberg (1954)). For example, numeric judgments can be affected by whether response scales use integral or decimal values, where the first judgment falls in the range of possibilities, and what range respondents expect to use (Poulton, 1989, 1994). That can be true even with familiar response modes, such that beliefs may differ when elicited in terms of probabilities and odds (Reference vonWinterfeldt and EdwardsvonWinterfeldt & Edwards, 1986). As a result, there is no unique Y% for each X%.
Such sensitivity to procedural detail also limits the generalizability of the studies used to support recalibration proposals. For example, one common task in those studies asks respondents to choose the more likely of two alternatives (e.g., absinthe is (a) a liqueur or (b) a precious stone), and then assign a probability (on the 0.5-1.0 range). Those judgments tend to be too high (indicating overconfidence) with relatively hard questions (e.g., 60% correct) and too low (indicating underconfidence) with relatively easy ones (e.g., 80% correct). A plausible explanation is that respondents enter the tasks expecting some difficulty level (e.g., getting 70% correct) and then anchor on that expectation, leaving their judgments too high for hard tasks and too low for easy ones (Reference Lichtenstein, Fischhoff, Phillips, Kahneman, Slovic and TverskyLichtenstein et al., 1982). If asked how many they got right after answering the questions, people often provide an answer that differs from their mean response (Reference Sniezek and BuckleySniezek & Buckley, 1991).
Because numeric responses are sensitive to procedural detail, recalibration could make matters worse, rather than better, for example, increasing judgments that should be decreased, depending on whether the task was easy or hard, relative to respondents’ expectations. As a result, recalibration requires matching the conditions of an elicitation session to those in studies in which miscalibration has been observed.
A better strategy, though, is to get better-calibrated responses in the first place. The best way to do that is to provide the conditions needed for any learning: prompt, unambiguous feedback, with clearly understood incentives for candid expressions of uncertainty, augmented by whatever insight the research can provide regarding the psychological processes involved in evaluating evidence (Reference Lichtenstein, Fischhoff, Phillips, Kahneman, Slovic and TverskyLichtenstein et al., 1982). The consistency checks that are part of formal expert elicitations (Reference Morgan and HenrionMorgan & Henrion, 1990; Reference O’Hagan, Buck, Daneshkhah and EiserO’Hagan et al., 2006) should help people to check their work. The success of those efforts, however, is an empirical question, obligating those who elicit judgments to evaluate their coherence and calibration. In the best case, those responses will prove to be probability judgments needing no recalibration. Reference Shlomi and WallstenShlomi and Wallsten (2010) provide a nice example, with observers able to see how and how well judges use probability numbers.
3 Conclusion
Many studies have found probability judgments to be miscalibrated, in the sense that they deviate from observed probabilities of being correct. Seeing that, it might be tempting to recalibrate the probabilities that people give to more realistic ones. This note identifies a limit to the kinds of recalibration that make sense. If one accepts our argument that the requirement that recalibrated probabilities be coherent (assumption c) and assumption e)) are benign, then global recalibration (other than the identity function) entails that the original elicited numbers do not obey the laws of probability. While this is not a surprise, given the results of the huge literature following the path of Kahneman and Tversky, it does mean that global recalibration is not a remedy for miscalibration of subjective probabilities.


