Hogg and Klugman use the truncated Pareto distribution with probability density function

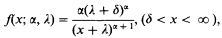
where δ≥0 is specified and α > 0 and λ > 0 are unknown parameters, to describe insurance claims. This is fitted first of all by the method of moments, using the estimators

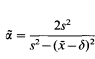
and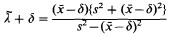

where 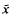is the mean of a simple random sample, and the (biased) variance

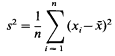
The authors then suggest, on pp. 113–16, that these estimates be used as starting values in a Newton iteration to get the maximum likelihood estimates of the parameters, but this technique can fail as a result of convergence problems. The object of this note is to show that this has led Hogg and Klugman to underestimate seriously the area in the tail of a fitted loss distribution, and to discuss a method of circumventing this difficulty.