No CrossRef data available.
Article contents
Sheppard's correction to the variance
Published online by Cambridge University Press: 11 August 2014
Extract
The variance of a continuous frequency distribution is often calculated by concentrating the frequencies in intervals of width h at the mid-points (vide Kendall, Advanced Theory of Statistics, Vol. 1, §3.16). Under certain conditions this approximation can be corrected by subtracting 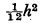 from the calculated variance. This note gives an interpretation in elementary terms of the ‘reason’ for such a correction.
from the calculated variance. This note gives an interpretation in elementary terms of the ‘reason’ for such a correction.
We consider three distributions, all having the same frequency in any one of the intervals of width h (Fig. 1):
C the original continuous distribution;
H where the frequency density is uniform within any one interval;
P where the frequency in an interval is concentrated at the mid-point.
- Type
- Research Article
- Information
- Copyright
- Copyright © Institute of Actuaries Students' Society 1948
References
* This assumption is justified in the last paragraph.


