Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-22T16:12:14.815Z Has data issue: false hasContentIssue false
  • English
  • Français

VARIATIONS OF BPS STRUCTURE AND A LARGE RANK LIMIT

Part of: Projective and enumerative geometry Equations of mathematical physics and other areas of application Symplectic geometry, contact geometry

Published online by Cambridge University Press:  12 March 2019

Jacopo Scalise  and
Jacopo Stoppa
Jacopo Scalise
Affiliation:
SISSA, via Bonomea 265, 34136Trieste, Italy ([email protected]; [email protected])
Jacopo Stoppa
Affiliation:
SISSA, via Bonomea 265, 34136Trieste, Italy ([email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We study a class of flat bundles, of finite rank 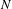$N$, which arise naturally from the Donaldson–Thomas theory of a Calabi–Yau threefold 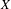$X$ via the notion of a variation of BPS structure. We prove that in a large 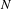$N$ limit their flat sections converge to the solutions to certain infinite-dimensional Riemann–Hilbert problems recently found by Bridgeland. In particular this implies an expression for the positive degree, genus 0 Gopakumar–Vafa contribution to the Gromov–Witten partition function of 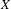$X$ in terms of solutions to confluent hypergeometric differential equations.

Keywords

Donaldson–Thomas theoryRiemann–Hilbert problemsGromov–Witten theory

MSC classification

Primary: 14N35: Gromov-Witten invariants, quantum cohomology, Gopakumar-Vafa invariants, Donaldson-Thomas invariants 35Q15: Riemann-Hilbert problems 53D45: Gromov-Witten invariants, quantum cohomology, Frobenius manifolds
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 1 , January 2021 , pp. 103 - 135
Check for updates
Copyright
© Cambridge University Press 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barbieri, A. and Stoppa, J., Frobenius type and CV-structures for Donaldson–Thomas theory and a convergence property, Comm. Anal. Geom. 27(3) (2019), to appear, arXiv:1512.01176 [math.AG].10.4310/CAG.2019.v27.n2.a2CrossRefGoogle Scholar
Barbieri, A., Stoppa, J. and Sutherland, T., A construction of Frobenius manifolds from stability conditions, Proc. Lond. Math. Soc. (2018), 1–39, doi:10.1112/plms.12217.Google Scholar
Bayer, A., Macrì, E. and Stellari, P., The space of stability conditions on abelian threefolds, and on some Calabi–Yau threefolds, Invent. Math. 206 (2016), 869–933.CrossRefGoogle Scholar
Bridgeland, T., Scattering diagrams, Hall algebras and stability conditions, Algebr. Geom. 4(5) (2017), 523–561.CrossRefGoogle Scholar
Bridgeland, T., Riemann–Hilbert problems from Donaldson–Thomas theory, Invent. Math., to appear, arXiv:1611.03697 [math.AG].Google Scholar
Bridgeland, T., Riemann–Hilbert problems for the resolved conifold, J. Differential Geom., to appear, arXiv:1703.02776 [math.AG].Google Scholar
Bridgeland, T. and Toledano-Laredo, V., Stokes factors and multilogarithms, J. Reine Angew. Math. 682 (2012), 89–128.Google Scholar
Chan, K., The Ooguri–Vafa metric, holomorphic discs and wall-crossing, Math. Res. Lett. 17(3) (2010), 401–414.10.4310/MRL.2010.v17.n3.a3CrossRefGoogle Scholar
Dubrovin, B., Geometry and integrability of topological–antitopological fusion, Commun. Math. Phys. 152(3) (1993), 539–564.10.1007/BF02096618CrossRefGoogle Scholar
Dubrovin, B., Geometry of 2D topological field theories, in Integrable Systems and Quantum Groups, Montecatini, Terme 1993, (ed. Francaviglia, M. and Greco, S.), Lecture Notes in Mathematics, Volume 1620, pp. 120–348 (Springer, Berlin, 1996).Google Scholar
Erdélyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F. G., Higher Transcendental Functions, Volume 1 (Krieger, New York, 1981).Google Scholar
Filippini, S., Garcia Fernandez, M. and Stoppa, J., Stability data, irregular connections and tropical curves, Sel. Math. New Ser. 23 (2017), 1355–1418.CrossRefGoogle Scholar
Fokas, A., Its, A., Kapaev, A. and Novokshenov, V., Painlevé Transcendents: the Riemann–Hilbert Approach, Mathematical Surveys and Monographs of the AMS, (American Mathematical Society, Providence, RI, 2006).CrossRefGoogle Scholar
Gaiotto, D., Opers and TBA, arXiv:1403.6137 [hep-th].Google Scholar
Gaiotto, D., Moore, G. and Neitzke, A., Four dimensional wall-crossing via three-dimensional field theory, Comm. Math. Phys. 299(1) (2010), 163–224.10.1007/s00220-010-1071-2CrossRefGoogle Scholar
Goncharov, A. B., Multiple polylogarithms and mixed Tate motives, arXiv:math/0103059 [math.AG].Google Scholar
Gross, M., Mirror Symmetry and the Strominger–Yau–Zaslow Conjecture, Current Developments in Mathematics, Volume 2012, pp. 133–191 (Int. Press, Somerville, MA, 2013).Google Scholar
Gross, M., Pandharipande, R. and Siebert, B., The tropical vertex, Duke Math. J. 153(2) (2010), 297–362.CrossRefGoogle Scholar
Hertling, C., tt ∗ geometry, Frobenius manifolds, their connections, and the construction for singularities, J. Reine Angew. Math. 555 (2003), 77–161.Google Scholar
Iwaki, K. and Nakanishi, T., Exact WKB analysis and cluster algebras, J. Phys. A: Math. Theor. 47 (2014), 474009.CrossRefGoogle Scholar
Joyce, D., Holomorphic generating functions for invariants counting coherent sheaves on Calabi–Yau 3-folds, Geom. Topol. 11 (2007), 667–725.CrossRefGoogle Scholar
Joyce, D. and Song, Y., A theory of generalized Donaldson–Thomas invariants, Mem. Amer. Math. Soc. 217(1020) (2012), iv + 199 pp. ISBN: 978-0-8218-5279-8.Google Scholar
Kontsevich, M. and Soibelman, Y., Stability structures, motivic Donaldson–Thomas invariants and cluster transformations, arXiv:0811.2435 [math.AG].Google Scholar
Kontsevich, M. and Soibelman, Y., Wall-crossing structures in Donaldson–Thomas invariants, integrable systems and mirror symmetry, in Homological Mirror Symmetry and Tropical Geometry, Lect. Notes Unione Mat. Ital., Volume 15, pp. 197–308 (Springer, Cham, 2014).CrossRefGoogle Scholar
Lin, Y.-S., Correspondence theorem between holomorphic discs and tropical discs on K3 surfaces, J. Differ. Geom., to appear, arXiv:1703.00411 [math.SG].Google Scholar
Mariño, M., Chern–Simons Theory, Matrix Models and Topological Strings, International Series of Monographs on Physics, Volume 131, (The Clarendon Press, Oxford University Press, Oxford, 2005), xii + 197 pp.CrossRefGoogle Scholar
Pirayatne, D. and Toda, Y., Moduli of Bridgeland semistable objects on 3-folds and Donaldson–Thomas invariants, J. Reine Angew. Math. 747 (2019), 175–220.CrossRefGoogle Scholar
Whittaker, E. T. and Watson, G. N., A Course of Modern Analysis, 4th edition (Cambridge University Press).10.1017/CBO9780511608759CrossRefGoogle Scholar