No CrossRef data available.
Published online by Cambridge University Press: 01 September 2022
We prove stronger variants of a multiplier theorem of Kislyakov. The key ingredients are based on ideas of Kislyakov and the Kahane–Salem–Zygmund inequality. As a by-product, we show various multiplier theorems for spaces of trigonometric polynomials on the n-dimensional torus 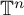 $\mathbb {T}^n$ or Boolean cubes
$\mathbb {T}^n$ or Boolean cubes 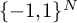 $\{-1,1\}^N$. Our more abstract approach based on local Banach space theory has the advantage that it allows to consider more general compact abelian groups instead of only the multidimensional torus. As an application, we show that various recent
$\{-1,1\}^N$. Our more abstract approach based on local Banach space theory has the advantage that it allows to consider more general compact abelian groups instead of only the multidimensional torus. As an application, we show that various recent 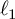 $\ell _1$-multiplier theorems for trigonometric polynomials in several variables or ordinary Dirichlet series may be proved without the Kahane–Salem–Zygmund inequality.
$\ell _1$-multiplier theorems for trigonometric polynomials in several variables or ordinary Dirichlet series may be proved without the Kahane–Salem–Zygmund inequality.