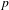Hostname: page-component-6bf8c574d5-gr6zb Total loading time: 0 Render date: 2025-02-16T16:55:27.580Z Has data issue: false hasContentIssue false
  • English
  • Français

UNRAMIFIEDNESS OF GALOIS REPRESENTATIONS ATTACHED TO HILBERT MODULAR FORMS MOD $p$ OF WEIGHT 1

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  23 April 2018

Mladen Dimitrov  and
Gabor Wiese
Mladen Dimitrov
Affiliation:
University of Lille, CNRS, UMR 8524 – Laboratoire Paul Painlevé, 59000 Lille, France ([email protected])
Gabor Wiese
Affiliation:
University of Luxembourg, Mathematics Research Unit, 6, avenue de la Fonte, L-4364 Esch-sur-Alzette, Luxembourg ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

The main result of this article states that the Galois representation attached to a Hilbert modular eigenform defined over 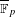$\overline{\mathbb{F}}_{p}$ of parallel weight 1 and level prime to 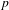$p$ is unramified above 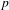$p$. This includes the important case of eigenforms that do not lift to Hilbert modular forms in characteristic 0 of parallel weight 1. The proof is based on the observation that parallel weight 1 forms in characteristic 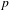$p$ embed into the ordinary part of parallel weight 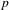$p$ forms in two different ways per prime dividing 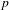$p$, namely via ‘partial’ Frobenius operators.

Keywords

Hilbert modular forms modulo pweight oneGalois representations

MSC classification

Primary: 11F80: Galois representations
Secondary: 11F41: Automorphic forms on $(2)$; Hilbert and Hilbert-Siegel modular groups and their modular and automorphic forms; Hilbert modular surfaces 11F33: Congruences for modular and $p$-adic modular forms
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 2 , March 2020 , pp. 281 - 306
Copyright
© Cambridge University Press 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andreatta, F. and Goren, E. Z., Hilbert modular forms: mod p and p-adic aspects, Mem. Amer. Math. Soc. 173(819) (2005), vi+100.Google Scholar
Buzzard, K., Diamond, F. and Jarvis, F., On Serre’s conjecture for mod ℓ Galois representations over totally real fields, Duke Math. J. 55 (2010), 105–161.Google Scholar
Buzzard, K. and Taylor, R., Companion forms and weight 1 forms, Ann. of Math. (2) 149 (1999), 905–919.Google Scholar
Calegari, F. and Geraghty, D., Modularity lifting theorems beyond the Taylor–Wiles method, Invent. Math. 211 (2018), 297–433.Google Scholar
Carayol, H., Formes modulaires et représentations galoisiennes à valeurs dans un anneau local complet, in p-adic Monodromy and the Birch and Swinnerton-Dyer Conjecture (Boston, MA, 1991), Contemp. Math., Volume 165, pp. 213–237. (1994).Google Scholar
Chai, C.-L., Arithmetic minimal compactification of the Hilbert–Blumenthal moduli space, Ann. of Math. (2) 131 (1990), 541–554.Google Scholar
Coleman, R. F. and Voloch, J. F., Companion forms and Kodaira–Spencer theory, Invent. Math. 110 (1992), 263–281.Google Scholar
Dasgupta, S., Darmon, H. and Pollack, R., Hilbert modular forms and the Gross–Stark conjecture, Ann. of Math. (2) 174 (2011), 439–484.Google Scholar
Deligne, P. and Pappas, G., Singularités des espaces de modules de Hilbert, en les caractéristiques divisant le discriminant, Compos. Math. 90 (1994), 59–79.Google Scholar
Deligne, P. and Serre, J.-P., Formes modulaires de poids 1, Ann. Sci. Éc. Norm. Supér. (4) 74 (1974), 507–530.Google Scholar
Dimitrov, M., Galois representations modulo p and cohomology of Hilbert modular varieties, Ann. Sci. Éc. Norm. Supér. (4) 38 (2005), 505–551.Google Scholar
Dimitrov, M., On Ihara’s lemma for Hilbert modular varieties, Compos. Math. 145 (2009), 1114–1146.Google Scholar
Dimitrov, M., Compactifications arithmétiques des variétés de Hilbert et formes modulaires de Hilbert pour 𝛤1(c, n), in Geometric Aspects of Dwork Theory, pp. 527–554 (Walter de Gruyter, Berlin, 2004).Google Scholar
Dimitrov, M. and Tilouine, J., Variétés et formes modulaires de Hilbert arithmétiques pour 𝛤1(c, n), in Geometric Aspects of Dwork Theory, pp. 555–614 (Walter de Gruyter, Berlin, 2004).Google Scholar
Edixhoven, S. J., The weight in Serre’s conjectures on modular forms, Invent. Math. 109 (1992), 563–594.Google Scholar
Emerton, M., Reduzzi, D. A. and Xiao, L., Unramifiedness of Galois representations arising from Hilbert modular surfaces, Forum Math. (2017), to appear.Google Scholar
Faltings, G. and Chai, C.-L., Degeneration of Abelian Varieties, Ergebnisse der Mathematik und ihrer Grenzgebiete (3), Volume 22 (Springer, Berlin, 1990). With an appendix by David Mumford, xii+316 pp.Google Scholar
Gee, T. and Kassaei, P., Companion forms in parallel weight 1, Compos. Math. 149 (2013), 903–913.Google Scholar
Gee, T., Liu, T. and Savitt, D., The weight part of Serre’s conjecture for GL(2), Forum Math. 3(e2) (2015), 52 pages.Google Scholar
Goren, E. and Kassaei, P., Canonical subgroups over Hilbert modular varieties, J. Reine Angew. Math. 670 (2012), 1–63.Google Scholar
Gross, B. H., A tameness criterion for Galois representations associated to modular forms (mod p), Duke Math. J. 61 (1990), 445–517.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique, Publ. Math. Hautes Etudes Sci., 4, 8, 11, 17, 20, 24, 28, 32 (1961).Google Scholar
Hida, H., p-adic Automorphic Forms on Shimura Varieties, Springer Monographs in Mathematics (Springer, New York, 2004).Google Scholar
Katz, N., p-adic L-functions for CM fields, Invent. Math. 49 (1978), 199–297.Google Scholar
Khare, C. and Wintenberger, J.-P., Serre’s modularity conjecture (I), Invent. Math. 178 (2009), 485–504.Google Scholar
Kisin, M. and Lai, K., Overconvergent Hilbert modular forms, Amer. J. Math. 127 (2005), 735–783.Google Scholar
Lan, K.-W. and Suh, J., Liftability of mod p cusp forms of parallel weights, Int. Math. Res. Not. IMRN 8 (2011), 1870–1879.Google Scholar
Ohta, M., Hilbert modular forms of weight 1 and Galois representations, in Automorphic Forms of Several Variables (Katata, 1983), Progress in Mathematics, Volume 46, pp. 333–352 (Birkhäuser Boston, Boston, MA, 1984).Google Scholar
Pappas, G., Arithmetic models for Hilbert modular varieties, Compos. Math. 98 (1995), 43–76.Google Scholar
Rogawski, J. D. and Tunnell, J. B., On Artin L-functions associated to Hilbert modular forms of weight 1, Invent. Math. 74 (1983), 1–42.Google Scholar
Rapoport, M., Compactification de l’espace de modules de Hilbert–Blumenthal, Compos. Math. 36 (1978), 255–335.Google Scholar
Raynaud, M., Faisceaux amples sur les schémas en groupes et les espaces homogènes, Lecture Notes in Mathematics, Volume 119 (Springer, Berlin-New York, 1970),ii+218 pp.Google Scholar
Serre, J.-P., Sur les représentations modulaires de degré 2 de Gal(ℚ/ℚ), Duke Math. J. 54 (1987), 179–230.Google Scholar
Shimura, G., The special values of the zeta functions associated with Hilbert modular forms, Duke Math. J. 45 (1978), 637–679.Google Scholar
The Stacks Project Authors, Stacks project, http://stacks.math.columbia.edu, 2016.Google Scholar
Taylor, R., On Galois representations associated to Hilbert modular forms, Invent. Math. 98 (1989), 265–280.Google Scholar
Van Hirtum, J., Explicit methods for Hilbert modular forms of weight 1, Preprint, 2017, arXiv:1710.02287.Google Scholar
Wiese, G., On Galois representations of weight one, Doc. Math. 19 (2014), 689–707.Google Scholar
Wiles, A., On p-adic representations for totally real fields, Ann. of Math. (2) 123 (1986), 407–456.Google Scholar
Wiles, A., On ordinary 𝜆-adic representations associated to modular forms, Invent. Math. 94 (1988), 529–573.Google Scholar