1.1 Charges, multipartitions and tableaux

Fix $e\in \mathbb {Z}_{\geq 2}$ throughout this paper.

We define a composition $\lambda $ of n to be a finite sequence of nonnegative integers $ (\lambda _1,\lambda _2, \ldots )$ whose sum $|\lambda | = \lambda _1+\lambda _2 + \dots $ equals n. We say that $\lambda $ is a partition if, in addition, this sequence is weakly decreasing. We let $\lambda ^t$ denote the transpose partition. An $\ell $ -multicomposition (respectively $\ell $ -multipartition or simply $\ell $ -partition) ${\boldsymbol {\lambda }}=(\lambda ^1,\lambda ^2,\ldots ,\lambda ^{\ell })$ of n is an $\ell $ -tuple of compositions (respectively partitions) such that $|{\boldsymbol {\lambda }}| := |\lambda ^1|+|\lambda ^2|+\ldots + |\lambda ^{\ell }|=n$ . We will denote the set of $\ell $ -multicompositions (respectively $\ell $ -partitions) of n by $\mathscr {C}_{\ell }(n)$ (respectively by $\mathscr {P}_{\ell }(n)$ ). Given ${\boldsymbol {\lambda }}=(\lambda ^1,\lambda ^2,\ldots ,\lambda ^{\ell }) \in \mathscr {P}_{\ell }(n)$ , the Young diagram of ${\boldsymbol {\lambda }}$ is defined to be the set of boxes (or nodes),

$$\begin{align*}\{(r,c,m) \mid 1\leq c\leq \lambda^m_r,\;1 \leq m \leq \ell \}. \end{align*}$$

We do not distinguish between the multipartition and its Young diagram. We draw the Young diagram of a partition by letting c increase from left to right and r increase from top to bottom. We refer to a box $(r,c,m)$ as being in the rth row and cth column of the mth component of ${\boldsymbol {\lambda }}$ . We draw the Young diagram of a multipartition by placing the Young diagrams of $\lambda ^1,\ldots ,\lambda ^{\ell }$ side by side from left to right as m runs from $1$ to $\ell $ . Finally, a tableau $\mathsf {T}$ on a multipartition ${\boldsymbol {\lambda }}$ is a bijection from the set of boxes of ${\boldsymbol {\lambda }}$ to $\{1, 2, \dots , |{\boldsymbol {\lambda }}|\}$ . The tableau $\mathsf {T}$ is called standard if it is increasing along the rows and columns of each component. We let $\mathrm { Std}({\boldsymbol {\lambda }})$ denote the set of all standard tableaux on ${\boldsymbol {\lambda }}$ . If $\mathsf {T} \in \mathrm { Std}({\boldsymbol {\lambda }})$ is a standard tableau, then $\operatorname {Shape}(\mathsf {T}{\downarrow }_{\{1,\dots ,k\}})$ is the multipartition whose Young diagram consists of all the boxes with labels $\leq k$ . Finally, we denote by $\varnothing $ the empty multipartition.

Example 1.2. Let $\ell =3$ and ${\boldsymbol {\lambda }}=(\lambda ^1,\lambda ^2,\lambda ^3)=((2,1),(4,2,1),(5))$ . We draw the Young diagram of ${\boldsymbol {\lambda }}$ as follows:

Note that the residue of a box in ${\boldsymbol {\lambda }}$ depends on the choice of the charge $\mathbf {s}\in \mathbb Z^{\ell }$ . For a tableau $\mathsf {T}$ on ${\boldsymbol {\lambda }}$ , we let ${\mathrm {res} (\mathsf {T})}$ denote the residue sequence consisting of $\mathrm {res} (\mathsf {T}^{-1}(k))$ for $k=1,\dots , n$ in order.

Example 1.4. Let $\ell =3$ and ${\boldsymbol {\lambda }}=(\lambda ^1,\lambda ^2,\lambda ^3)=((2,1),(4,2,1),(5))$ . Let $\mathbf {s}=(-1,2,0)\in \mathbb {Z}^3$ . The Young diagram of ${\boldsymbol {\lambda }}$ with its boxes labelled by their charged contents looks as follows:

Now, take $e=4$ , then labelling the boxes of the Young diagram of ${\boldsymbol {\lambda }}$ their residues, we have:

and we have that $ \mathrm {res}(\mathsf {T}_{{\boldsymbol {\lambda }}})= (0,2,1,0,3,2,1,3,2,0,2,0,3,1,0) \in ( \mathbb Z / e \mathbb Z)^{15},$ where $\mathsf {T}_{{\boldsymbol {\lambda }}}$ is the reverse column-reading tableau on ${\boldsymbol {\lambda }}$ ; see Example 1.10 below.

Example 1.10. Definition 1.9 is best illustrated via an example. Let $\mathbf {s} =(0,3,4 )$ with $e=7$ . We have that $\lambda =((2,1),(4,2,1),(5))\in \mathscr {P}_{(2,3,1)}(15)$ and that $h_1=2<7+0-4=e+s_1-s_{\ell }$ and so $m=1$ is a step change (one can check that this step change is unique). The reverse reading column reading tableau $\mathsf {T}_{1,{\boldsymbol {\lambda }}}$ is given by filling the first columns of the third component, second component, first component and then the second columns of these components…hence obtaining

Given ${\boldsymbol {\lambda }} \in \mathscr {P}_{\underline {h}}(n)$ , we let $\mathrm {Add}_{\underline {h}}({\boldsymbol {\lambda }})$ (respectively $\mathrm {Rem}_{\underline {h}}({\boldsymbol {\lambda }})$ ) denote the set of all addable (respectively removable) boxes of the Young diagram so that the resulting Young diagram is the Young diagram of a multipartition belonging to $\mathscr {P}_{\underline {h}}(n+1)$ (respectively $\mathscr {P}_{\underline {h}}(n-1)$ ). We let $\mathrm {Add}^i_{\underline {h}}({\boldsymbol {\lambda }})$ (respectively $\mathrm {Rem}^i_{\underline {h}}({\boldsymbol {\lambda }})$ ) denote the subset of nodes of residue equal to $i\in {\mathbb {Z}}/e{\mathbb {Z}}$ . Dropping the subscript ${\underline {h}}$ , we obtain the usual sets of addable and removable i-nodes of a multipartition.

Definition 1.11. Given $1\leq k\leq n$ and a standard tableau $\mathsf {T}$ on a multipartition ${\boldsymbol {\lambda }}$ , we let ${\mathcal A} _{\mathsf {T}}(k)$ (respectively ${\mathcal R} _{\mathsf {T}}(k)$ ) denote the set of all addable $\mathrm {res} (\mathsf {T}^{-1}(k))$ -boxes (respectively all removable $\mathrm {res} (\mathsf {T}^{-1}(k))$ -boxes) of the multipartition $\operatorname {Shape}(\mathsf {T}{\downarrow }_{\{1,\dots ,k\}})$ which are more dominant than $\mathsf {T}^{-1}(k)$ . We define the degree of $\mathsf {T}\in \mathrm {Std}({\boldsymbol {\lambda }})$ for ${\boldsymbol {\lambda }} \in \mathscr {P} (n)$ as follows:

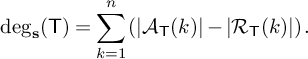$$ \begin{align*} \deg_{\mathbf{s} } (\mathsf{T}) = \sum_{k=1}^n \left( |{\mathcal A} _{\mathsf{T}}(k)|-|{\mathcal R} _{\mathsf{T}}(k)| \right). \end{align*} $$

1.2 The $\widehat {\mathfrak {sl}}_e$ -crystal

Ariki proved that the $\widehat {\mathfrak {sl}}_e$ -crystal explicitly realises the modular branching rule of the cyclotomic Hecke algebra [Reference Ariki3]. We now recall the combinatorics of this construction. Fix $e\geq 2$ and a charge $\mathbf {s} \in \mathbb {Z}^{\ell }$ . The $\widehat {\mathfrak {sl}}_e$ -crystal is a simply directed graph on the set of vertices consisting of all $\ell $ -partitions. Its arrows are given by a rule for adding at most one box of each residue $i\in \mathbb {Z}/e\mathbb {Z}$ to a given $\ell $ -partition. We define the crystal operators $\tilde {e}_i$ and $\tilde {f}_i$ , which remove and add (respectively) at most one box of residue i.

The $\widehat {\mathfrak {sl}}_e$ -crystal is in general disconnected, and we will be interested in its connected component containing the empty multipartition $\varnothing $ . The vertices in this connected component of the $\widehat {\mathfrak {sl}}_e$ -crystal do not, in general, admit closed formulas (one must instead search for a sequence of good nodes by repeated use of Definition 1.13). However, for our choice of cylindric charge $\mathbf {s} \in {\mathbb {Z}}^{\ell }$ (as in Definition 1.1), we have the following combinatorial description from [Reference Foda, Leclerc, Okado, Thibon and Welsh27].

2.1 The affine Hecke algebra

Let us recall that the (extended) affine braid group, $B^{ea}_{n}$ has generators $T_{1}, \dots , T_{n-1}, x_{1}, \dots , x_{n}$ subject to the following relations:

1. (a) $T_{i}T_{i+1}T_{i} = T_{i+1}T_{i}T_{i+1}$ and $T_{i}T_{j} = T_{j}T_{i}$ if $|i - j|> 1$ .

2. (b) $x_{i}x_{j} = x_{j}x_{i}$ for every $i, j = 1, \dots , n$ .

3. (c) $T_{i}x_{i}T_{i} = x_{i+1}$ , $T_{i}x_{j} = x_{j}T_{i}$ if $j \neq i, i+1$ .

We may think of $B^{ea}_{n}$ as the braid group on the cylinder. The element $T_{i}$ corresponds to the usual braid generator that crosses two adjacent strands, and the element $x_{i}$ corresponds to looping the ith strand around the cylinder so that it comes back to the ith position; see Figure 1 below.

Figure 1 The braid generators $x_{i}$ and $T_{i}$ . We remark that these are braids on a cylinder, so the left and right sides of the rectangles are to be identified.

The affine Hecke algebra is the quotient of the group algebra of $B^{ea}_{n}$ by a skein-type relation.

Definition 2.1. Let $\mathsf {R}$ be a domain and $q \in \mathsf {R}^{\times }$ , $q \neq \pm 1$ . The (extended) affine Hecke algebra $\mathcal {H}^{\mathsf {aff}}_{q}(n, \mathsf {R})$ is the quotient of the group algebra $\mathsf {R}B^{ea}_{n}$ by the relations

$$ \begin{align*}(T_{i} + 1)(T_{i} - q) = 0 \end{align*} $$

for $i = 1, \dots , n-1$ . When the domain $\mathsf {R}$ is clear from the outset, we will simply denote the affine Hecke algebra by $\mathcal {H}^{\mathsf {aff}}_{q}(n)$ .

When $\mathsf {R}$ is a domain of characteristic zero it is known (see, for example, [Reference Chriss and Ginzburg20, Proposition 7.1.14]) that the center of $\mathcal {H}^{\mathsf {aff}}_{q}(n)$ is $Z(\mathcal {H}^{\mathsf {aff}}_{q}(n)) = \mathbb {A}^{S_{n}}$ , the algebra of symmetric Laurent polynomials in the Jucys–Murphy elements. Thus, $\mathcal {H}^{\mathsf {aff}}_{q}(n)$ is finite over its center, and, when $\mathsf {R}$ is a field $\mathsf {F}$ of characteristic zero, every irreducible representation of $\mathcal {H}^{\mathsf {aff}}_{q}(n)$ is finite-dimensional. If moreover $\mathsf {F}$ is algebraically closed it follows, looking at the eigenvalues of $X_{1}$ , that every irreducible representation of $\mathcal {H}^{\mathsf {aff}}_{q}(n)$ factors through an algebra of the form

$$ \begin{align*}\mathcal{H}_{q, Q_1, \dots, Q_{\ell}}(n) := \frac{\mathcal{H}^{\mathsf{aff}}_{q}(n)}{\left(\prod_{i}^{\ell}(X_{1} - Q_{i})\right).} \end{align*} $$

This is known as the cyclotomic Hecke algebra, or the Ariki–Koike algebra. It is a finite-dimensional $\mathsf {F}$ -algebra, of dimension precisely $n!\ell ^{n}$ , [Reference Ariki and Koike1].

2.2 Unitary representations

For this subsection, we let $\mathsf {R} = \mathbb {C}$ , the complex field. We make the convention that a Hermitian form on a finite-dimensional complex vector space is linear on the first variable and conjugate-linear on the second. Recall that we have defined the affine Hecke algebra $\mathcal {H}^{\mathsf {aff}}_{q}(n)$ as a quotient of the group algebra $\mathbb {C}B^{ea}_{n}$ , so the following notion makes sense.

Note that all affine Hecke algebras admit a one-dimensional unitary representation, where all elements $T_{i}$ act by $-1$ . However, unless q is a root of unity this may be the only unitary representation, as the following result shows.

Proof. Let $m \in M$ and i be as in the statement of the lemma. Then,

$$ \begin{align*}0 \neq q\langle m, m \rangle = \langle T_{i}m, m \rangle = \langle m, T_{i}^{-1}m\rangle = \overline{q^{-1}}\langle m, m\rangle \end{align*} $$

so that $q = \overline {q^{-1}}$ . Thus, q is in the unit circle.

Since every cyclotomic Hecke algebra $\mathcal {H}_{q, Q_1, \dots , Q_{\ell }}(n)$ is a quotient of the affine Hecke algebra, it makes sense to speak about unitary representations of $\mathcal {H}_{q, Q_1, \dots , Q_{\ell }}(n)$ . Just as in Lemma 2.6, we have that if $\mathcal {H}_{q, Q_1, \dots , Q_{\ell }}(n)$ admits a unitary representation, then all complex numbers $q, Q_1, \dots , Q_{\ell } \in \mathbb {C}^{\times }$ must lie in the unit circle.

Let us remark that the cyclotomic Hecke algebra $\mathcal {H}_{q, Q_1, \dots , Q_{\ell }}(n)$ is a quotient of the group algebra of a different braid group: the braid group $B(\ell , 1, n)$ , which is defined as follows. Let $G(\ell , 1, n) := S_{n} \ltimes (\mathbb {Z}/\ell \mathbb {Z})^{n}$ be the cyclotomic group. If we think of this group as the group of $n \times n$ permutation matrices whose nonzero entries are $\ell $ -roots of unity, we get an action of $G(\ell , 1, n)$ on $\mathfrak {h} := \mathbb {C}^{n}$ . Let $\mathfrak {h}^{reg}$ be the locus where this action is free. It can be shown that this is the complement of a hyperplane arrangement in $\mathbb {C}^n$ . Then,

$$ \begin{align*} B(\ell, 1, n) := \pi_{1}(\mathfrak{h}^{reg}/G(\ell, 1, n)). \end{align*} $$

For example, when $\ell = 1$ , the group $B(1, 1, n)$ is the usual Artin braid group on n strands. It is clear from the definitions (see, e.g., [Reference Broué, Malle and Rouquier16]) that a $\mathcal {H}_{q, Q_1, \dots , Q_{\ell }}(n)$ -representation is unitary if and only if it admits a positive-definite $B(\ell , 1, n)$ -invariant Hermitian form. On the other hand, Rouquier has shown using the representation theory of rational Cherednik algebras, [Reference Shelley-Abrahamson51, Proposition 4.5.4], that every irreducible $\mathcal {H}_{q, Q_1, \dots , Q_{\ell }}(n)$ -representation admits a (unique up to $\mathbb {R}^{\times }$ -scalars) nondegenerate $B(\ell , 1, n)$ -invariant Hermitian form. Thus, the question of unitarity is that of positive-definiteness of this form.

2.3 Unitary representations via $*$ -operations

In [Reference Barbasch and Ciubotaru6], Barbasch and Ciubotaru define a class of representations that are closely related to the unitary representations we study in this paper. The goal of this section is to explore this relation. In order to do so, throughout this subsection $\mathsf {R} = \mathbb {C}[\mathsf {q}, \mathsf {q}^{-1}]$ and $\mathcal {H}^{\mathsf {aff}}_{\mathsf {q}}(n) := \mathcal {H}^{\mathsf {aff}}_{\mathsf {q}}(n, \mathsf {R})$ .

Definition 2.8. A $*$ -operation on $\mathcal {H}^{\mathsf {aff}}_{\mathsf {q}}(n)$ is a conjugate-linear, involutive antiautomorphism of $\mathcal {H}^{\mathsf {aff}}_{\mathsf {q}}(n)$ . Given a $*$ -operation on $\mathcal {H}^{\mathsf {aff}}_{\mathsf {q}}(n)$ , a representation M of $\mathcal {H}^{\mathsf {aff}}_{\mathsf {q}}(n)$ is called $*$ -unitary if it admits a positive-definite Hermitian form which is $\mathcal {H}^{\mathsf {aff}}_{\mathsf {q}}(n)$ -invariant in the sense that

$$ \begin{align*}\langle am, m'\rangle = \langle m, a^{*}m'\rangle \end{align*} $$

for every $m, m' \in M$ , $a \in \mathcal {H}^{\mathsf {aff}}_{\mathsf {q}}(n)$ .

In [Reference Barbasch and Ciubotaru6], the authors define $*$ -operations on $\mathcal {H}^{\mathsf {aff}}_{\mathsf {q}}(n)$ and study the notion of unitary representations for these $*$ -operations. These are the first two $*$ -operations of the following proposition.

Proof. For $\bullet $ and $\star $ , see [Reference Barbasch and Ciubotaru6, Definition 2.3.1]. For $\dagger $ , note that the relation $(T_{i}+1)(T_{i}-\mathsf {q}) = 0$ is equivalent to $(T_{i}^{-1} + 1)(T_{i}^{-1} - \mathsf {q}^{-1}) = 0$ , so this is preserved under $\dagger $ . It is also clear that $\dagger $ preserves the relations among the $X_{i}$ , as well as the braid relations among the $T_{i}$ . Finally, we have

$$ \begin{align*}(T_{i}X_{i}T_{i})^{\dagger} = T_{i}^{\dagger}X_{i}^{\dagger}T_{i}^{\dagger} = T_{i}^{-1}X_{i}^{-1}T_{i}^{-1} = (T_{i}X_{i}T_{i})^{-1} = \mathsf{q}^{-1}X_{i+1}^{-1} = (\mathsf{q} X_{i+1})^{\dagger} \end{align*} $$

which finishes the proof.

It is clear that a representation M of $\mathcal {H}^{\mathsf {aff}}_{\mathsf {q}}(n)$ is unitary in the sense of Definition 2.5 if and only if it is $\dagger $ -unitary in the sense of [Reference Barbasch and Ciubotaru6]. Representations that are $\star $ -unitary and $\bullet $ -unitary have been studied in loc. cit., where they are shown to be related to unitary representations of general linear groups over p-adic fields. Note that both $\bullet $ and $\star $ commute with the action of $\mathsf {q}$ , while $\dagger $ does not. Nevertheless, the $*$ -operations $\bullet $ and $\dagger $ are closely related, as witnessed by the following result.

Proof. That $\iota $ defines a $\mathbb {C}$ -linear involutive algebra automorphism is easy to check from the relations on $\mathcal {H}^{\mathsf {aff}}_{\mathsf {q}}(n)$ . Since $\iota $ is $\mathbb {C}$ -linear while $\dagger $ is conjugate linear, both compositions $\iota \circ \dagger $ and $\dagger \circ \iota $ are conjugate linear. Also, since $\iota $ is an automorphism while $\dagger $ is an antiautomorphism, both $\iota \circ \dagger $ and $\dagger \circ \iota $ are antiautomorphisms. Thus, it suffices to check the equality $\iota \circ \dagger = \bullet = \dagger \circ \iota $ on generators $T_{i}, X_{i}$ and $\mathsf {q}$ .

$$ \begin{align*}\iota(T_{i}^{\dagger}) = \iota(T_{i}^{-1}) = T_{i} = T_{i}^{\bullet}, \iota(X_{i}^{\dagger}) = \iota(X_{i}^{-1}) = X_{i} = X_{i}^{\bullet}, \iota(\mathsf{q}^{\dagger}) = \iota(\mathsf{q}^{-1}) = \mathsf{q} = \mathsf{q}^{\bullet} \end{align*} $$

$$ \begin{align*}\iota(T_{i})^{\dagger} = (T_{i}^{-1})^{\dagger} = T_{i} = T_{i}^{\bullet}, \iota(X_i)^{\dagger} = (X_i^{-1})^{\dagger} = X_i = X_i^{\bullet}, \iota(\mathsf{q})^{\dagger} = (\mathsf{q}^{-1})^{\dagger} = \mathsf{q} = \mathsf{q}^{\bullet}, \end{align*} $$

and the result follows.

We remark, however, that we do not obtain an equivalence between categories of $\dagger $ -unitary and $\bullet $ -unitary representations. To do this, we must find an automorphism $\varphi $ of $\mathcal {H}^{\mathsf {aff}}_{\mathsf {q}}(n)$ satisfying $\varphi \circ \dagger \circ \varphi ^{-1} = \bullet $ . It is unlikely that such an automorphism exists, at least in the algebraic setting. Roughly speaking, if an irreducible representation is $\dagger $ -unitary, then we must have that $\mathsf {q}$ acts by a complex number of norm $1$ while, if a representation is $\bullet $ -unitary then $\mathsf {q}$ must act by a real number. It is possible that one may obtain equivalences between $\dagger $ -unitary and $\bullet $ -unitary representations by working with representations of the formal affine Hecke algebra [Reference Hoffnung, Malagón-López, Savage and Zainoulline35] so that we can take exponential and logarithms of the variable $\hbar $ (that should be thought of as $\log (\mathsf {q})$ ), but we do not do it here.

2.4 Unitary representations are calibrated

We go back to the setting of $\mathsf {R} = \mathbb {C}$ . Moreover, throughout this section, we let $q \in \mathbb {C}^{\times }$ be in the unit circle. Let us recall the following important notion from the representation theory of affine Hecke algebras [Reference Ram46].

For a $\mathcal {H}^{\mathsf {aff}}_{q}(n)$ -module and a vector $\mathbf {a} = (a_1, \dots , a_n) \in (\mathbb {C}^{\times })^n$ , we define the $\mathbf {a}$ -weight space to be

$$ \begin{align*} M_{\mathbf{a}} := \{m \in M \mid X_{i}m = a_{i}m \; \text{for every} \; i = 1, \dots, n\}. \end{align*} $$

Thus, every unitary $\mathcal {H}^{\mathsf {aff}}_q(n)$ -module is the direct sum of its weight spaces.

Proof. Statement (1) is clear; see, for example, Remark 2.7. To prove (2), assume that both $M_{\mathbf {a}}$ and $M_{\mathbf {b}}$ are both nonzero; let $m_1 \in M_{\mathbf {a}}$ , $m_2 \in M_{\mathbf {b}}$ and i such that $a_{i} \neq b_{i}$ . Then,

$$ \begin{align*} a_i\langle m_1, m_2\rangle = \langle X_{i}m_1, m_2\rangle = \langle m_1, X_{i}^{-1}m_2\rangle = \overline{b_{i}^{-1}}\langle m_1, m_2\rangle. \end{align*} $$

Since $a_{i} \neq b_{i}$ and, by (1), $|a_i| = |b_i| = 1$ , we obtain $\overline {a_i} \neq b_{i}^{-1}$ . Thus, we have $\langle m_1, m_2\rangle = 0$ , as required.

2.5 When are calibrated representations unitary?

The purpose of this section is to obtain necessary and sufficient conditions for a calibrated representation to be unitary. We have seen one condition a calibrated representation must satisfy in order to be unitary: All the weights appearing in it must have values in the unit circle. This necessary condition is, however, not sufficient. To obtain a complete answer, we must first recall the classification of irreducible calibrated representations in terms of the weights that appear in them. This is from [Reference Ram46], and we follow loc. cit closely.

Definition 2.16 [Reference Ram46]

We say that a weight $\mathbf {a} = (a_{1}, \dots , a_{n}) \in (\mathbb {C}^{\times })^{n}$ is calibrated if the following condition holds:

$$ \begin{align*} \mathrm{For \ every} \ i < j \ \mathrm{such \ that} \ a_{i} = a_{j}, qa_{i}, q^{-1}a_{i} \in \{a_{i+1}, \dots, a_{j-1}\}. \end{align*} $$

Since we are assuming that $q \neq \pm 1$ note, in particular, that if $\mathbf {a}$ is a calibrated weight, then $a_{i} \neq a_{i+1}$ , $a_{i} \neq a_{i+2}$ for every i. We denote by $\mathfrak {C}^{\operatorname {\mathrm {aff}}} \subseteq (\mathbb {C}^{\times })^{n}$ the set of all calibrated weights.

For a calibrated weight $\mathbf {a} \in \mathfrak {C}^{\operatorname {\mathrm {aff}}}$ , we say that $s_{i} = (i, i+1) \in S_{n}$ is an admissible transposition if $a_{i+1} \neq q^{\pm 1}a_{i}$ . Note that, if $s_{i}$ is an admissible transposition, then $s_{i}\mathbf {a} \in \mathfrak {C}^{\operatorname {\mathrm {aff}}}$ .

The following result is due to Ram, [Reference Ram46]. It can be thought of as asserting the existence of a Young seminormal form for calibrated representations.

Theorem 2.18. Let $[\mathbf {a}] \in \mathfrak {C}^{\operatorname {\mathrm {aff}}}/\sim $ be an equivalence class. Then, there exists an irreducible calibrated module $M_{[\mathbf {a}]}$ whose weights are precisely $[\mathbf {a}]$ . More precisely, M has a basis $w_{\mathbf {b}}$ , $\mathbf {b} \in [\mathbf {a}]$ , and the action of $\mathcal {H}^{\mathsf {aff}}_{q}(n)$ is given as follows:

$$ \begin{align*}X_{i}w_{\mathbf{b}} = b_{i}w_{\mathbf{b}}, \hspace{1cm} T_{i}w_{\mathbf{b}} &= \frac{b_{i+1}(q-1)}{b_{i+1} - b_{i}}w_{\mathbf{b}} \\ &\quad + (1 - \delta_{qb_{i}, b_{i+1}})(1 - \delta_{q^{-1}b_{i}, b_{i+1}})\left[-q + \frac{b_{i+1}(q-1)}{b_{i+1}-b_{i}}\right]w_{s_{i}\mathbf{b}}, \end{align*} $$

where we define $w_{s_{i}\mathbf {b}} = 0$ if $s_{i}$ is not an admissible transposition for $\mathbf {b}$ . Moreover, every irreducible calibrated module is of the form $M_{[\mathbf {a}]}$ for a unique equivalence class $[\mathbf {a}] \in \mathfrak {C}^{\operatorname {\mathrm {aff}}}/\sim $ .

We will characterize the calibrated weights $\mathbf {a}$ for which $M_{[\mathbf {a}]}$ is indeed unitary. Since every unitary representation is semisimple, this would give us all the unitary representations of $\mathcal {H}^{\mathsf {aff}}_{q}(n)$ . First, we have seen in Lemma 2.15 that a necessary condition is that $\mathbf {a} \in (S^1)^{n}$ , where $S^1 \subseteq \mathbb {C}$ is the unit circle. Note that Theorem 2.18 tells us that every weight space in $M_{[\mathbf {a}]}$ is one-dimensional and, as we have seen in Lemma 2.15, different weight spaces must be orthogonal under an invariant, positive-definite Hermitian form.

So let $\langle \cdot , \cdot \rangle $ be an invariant, nondegenerate Hermitian form on $M_{[\mathbf {a}]}$ , and assume that $\mathbf {a} \in (S^1)^n$ . By [Reference Shelley-Abrahamson51, Proposition 4.5.4], such a form exists. By our discussion in the previous paragraph, there exist numbers $A_{\mathbf {b}} \in \mathbb {R}$ , $\mathbf {b} \in [\mathbf {a}]$ such that

(2.19) $$ \begin{align} \langle w_{\mathbf{b}}, w_{\mathbf{b}'}\rangle = A_{\mathbf{b}}\delta_{\mathbf{b}, \mathbf{b}',} \end{align} $$

and our job is to find conditions on $[\mathbf {a}]$ guaranteeing that all numbers $A_{\mathbf {b}}$ can be chosen to have the same sign. We separate in several cases, and we make heavy use of the Young seminormal form of Theorem 2.18.

Case 1. $\mathbf {b}' \neq \mathbf {b}, s_{i}\mathbf {b}$ . In this case, we have $\langle T_{i}w_{\mathbf {b}}, w_{\mathbf {b}'}\rangle = \langle w_{\mathbf {b}}, T_{i}^{-1}w_{\mathbf {b}'}\rangle = 0$ .

Case 2. $\mathbf {b}' = \mathbf {b}$ . In which case,

$$ \begin{align*} \langle T_{i}w_{\mathbf{b}}, w_{\mathbf{b}}\rangle = A_{\mathbf{b}}\displaystyle{\tfrac{b_{i+1}(q-1)}{b_{i+1} - b_{i}}}. \end{align*} $$

On the other hand, since $T_{i}^{-1} = q^{-1}(T_{i} + 1-q)$ then, using the fact that $\overline {q} = q^{-1}$ , $\overline {b_{i+1}} = b_{i+1}^{-1}$ and $\overline {b_{i}} = b_{i}^{-1}$ , we have that

$$ \begin{align*} \langle w_{\mathbf{b}}, T_{i}^{-1}w_{bb}\rangle & = q\langle w_{\mathbf{b}}, (T_{i} + 1-q)w_{\mathbf{b}}\rangle\\ &= qA_{\mathbf{b}}\overline{\left[\tfrac{b_{i+1}(q-1)}{b_{i+1} - b_{i}} + (1-q)\right]} \\ & = qA_{\mathbf{b}}\overline{\left[\tfrac{b_{i}(q-1)}{b_{i+1} - b_{i}}\right]} \\ &= A_{\mathbf{b}}\tfrac{b_{i+1}(1-q)}{b_{i} - b_{i+1}} \\ &= \langle T_{i}w_{\mathbf{b}}, w_{\mathbf{b}}\rangle. \end{align*} $$

Case 3. $\mathbf {b}' = s_{i}\mathbf {b}$ . Since in this case $s_{i}\mathbf {b}$ is defined, we have that $b_{i+1} \neq q^{\pm 1}b_{i}$ , so

$$ \begin{align*} \langle T_{i}w_{\mathbf{b}}, w_{s_{i}\mathbf{b}}\rangle = A_{s_{i}\mathbf{b}}\left(-q + \tfrac{b_{i+1}(q-1)}{b_{i+1}-b_{i}}\right) = A_{s_{i}\mathbf{b}} \left(\tfrac{qb_{i} - b_{i+1}}{b_{i+1} - b_{i}} \right). \end{align*} $$

On the other hand,

$$ \begin{align*} \langle w_{\mathbf{b}}, T_{i}^{-1}w_{s_{i}\mathbf{b}}\rangle & = q\langle w_{\mathbf{b}}, T_{i}w_{s_{i}\mathbf{b}}\rangle \\ & = qA_{\mathbf{b}}\left[\overline{-q + \left(\tfrac{b_{i}(q - 1)}{b_{i} - b_{i+1}}\right)}\right] \\ & = qA_{\mathbf{b}}\left[\tfrac{\overline{q}\overline{b_{i+1}} - \overline{b_{i}}}{\overline{b_{i}} - \overline{b_{i+1}}}\right] \\ & = A_{\mathbf{b}}\left[\tfrac{\overline{b_{i+1}} - q\overline{b_{i}}}{\overline{b_{i}} - \overline{b_{i+1}}} \right] \\ & = A_{\mathbf{b}}\left( \tfrac{b_{i} - qb_{i+1}}{b_{i+1} - b_{i}}\right). \end{align*} $$

And we see that, if the form $\langle \cdot , \cdot \rangle $ is to be $\mathcal {H}^{\mathsf {aff}}_{q}(n)$ -invariant, we must have

(2.20) $$ \begin{align} \frac{A_{s_{i}\mathbf{b}}}{A_{\mathbf{b}}} = \frac{b_{i} - qb_{i+1}}{qb_{i} - qb_{i+1}} = \frac{q - (b_{i}/b_{i+1})}{1 - q(b_{i}/b_{i+1})}, \end{align} $$

and, if the form $\langle \cdot , \cdot \rangle $ is to be positive-definite, we must have $A_{s_{i}\mathbf {b}}/A_{\mathbf {b}}> 0$ (note that manifestly $A_{s_{i}\mathbf {b}}/A_{\mathbf {b}} \in \mathbb {R}$ , as needed). Set $x = b_{i}/b_{i+1}$ . Now,

$$ \begin{align*} \frac{q - x}{1 - qx} = \frac{(q-x)(1 - \overline{qx})}{|1 - qx|^2} = 2\frac{\Re(q) - \Re(x)}{|1 - qx|^2}, \end{align*} $$

so $A_{s_{i}\mathbf {b}}/A_{\mathbf {b}}> 0$ if and only if $\Re (b_{i}/b_{i+1}) < \Re (q)$ , where $\Re (z)$ denotes the real part of $z\in \mathbb C$ .

So, assume that every $\mathbf {b} \in [\mathbf {a}]$ satisfies that $\Re (b_{i+1}/b_{i}) < \Re (q)$ for every pair $b_{i}, b_{i+1}$ with $b_{i}/b_{i+1} \neq 1, q^{\pm 1}$ . Start with any $\mathbf {b} \in [\mathbf {a}]$ . Any other $\mathbf {b}' \in [\mathbf {a}]$ is reachable from $\mathbf {b}$ by a sequence of admissible transpositions. We declare $\langle w_{\mathbf {b}}, w_{\mathbf {b}}\rangle = 1$ . By [Reference Shelley-Abrahamson51, Proposition 4.5.4], there is an invariant Hermitian form on $M_{[\mathbf {a}]}$ satisfying this, and we can see that we have:

$$ \begin{align*}\langle w_{s_{i_{t}}\dots s_{i_{1}}\mathbf{b}}, w_{s_{i_{t}}\dots s_{i_{1}}\mathbf{b}}\rangle = \frac{q(s_{i_{t-1}}\dots s_{i_{1}}\mathbf{b})_{i_{t} + 1} - (s_{i_{t-1}}\dots s_{i_{1}}\mathbf{b})_{i_{t}}}{(s_{i_{t-1}}\dots s_{i_{1}}\mathbf{b})_{i_{t} + 1} - q(s_{i_{t-1}}\dots s_{i_{1}}\mathbf{b})_{i_{t}}}\langle w_{s_{i_{t-1}}\dots s_{i_{1}}\mathbf{b}}, w_{s_{i_{t-1}}\dots s_{i_{1}}\mathbf{b}}\rangle. \end{align*} $$

We have arrived at the following result.

The following easy lemma will be useful in the future.

We now focus on representations that factor through a fixed cyclotomic quotient of $\mathcal {H}^{\mathsf {aff}}_q(n)$ .

2.6 Unitary modules for the cyclotomic Hecke algebra

Now, we seek to classify unitary representations of the cyclotomic Hecke algebra:

$$ \begin{align*} \mathcal{H}_{q, Q_1, \dots, Q_{\ell}}(n) = \frac{\mathcal{H}_{q}^{\operatorname{\mathrm{aff}}}(n)}{(\prod_{i = 1}^{\ell}X_{1} - Q_{i})}. \end{align*} $$

We may and will assume that all complex numbers $q, Q_1, \dots , Q_{\ell }$ live in the unit circle. Similarly to the case of the finite Hecke algebra $H_{q}(n)$ , we can see that if M is a calibrated representation of $\mathcal {H}_{q, Q_1, \dots , Q_{\ell }}(n)$ and $\mathbf {a}$ is a weight of M, then, for every $i = 1, \dots , n$ there exist $j \in 1, \dots , \ell $ and $m_{i} \in \mathbb {Z}$ such that $a_{i} = Q_{j}q^{m_{i}}$ . This implies the following result, which is Theorem A from the introduction.

The parameters $q, Q_1, \dots , Q_{\ell }$ of the form appearing in Lemma 2.23 are the most interesting ones from a representation-theoretic point of view. They are those for which the representation theory of the algebra $\mathcal {H}_{q, Q_1, \dots , Q_{\ell }}(n)$ cannot be broken up into smaller pieces. More precisely, let us define an equivalence relation on the set of parameters $Q_1, \dots , Q_{\ell }$ by declaring $Q_{i} \sim Q_{j}$ if $Q_{i}/Q_{j}$ is an integral power of q. Let $\mathcal {E}_{1}, \dots , \mathcal {E}_{k}$ be the different equivalence classes. Thanks to work of Dipper and Mathas (see, e.g., [Reference Ariki2, Theorem 13.30]), we have a category equivalence

(2.24) $$ \begin{align} \mathcal{H}_{q, Q_{1}, \dots, Q_{\ell}}(n)\operatorname{-mod} \cong \bigoplus_{n_1 + \dots + n_{k} = n} \bigotimes_{i = 1}^{k}\mathcal{H}_{q, \mathcal{E}_{i}}(n_{i})\operatorname{-mod}, \end{align} $$

where $\mathcal {H}_{q, \mathcal {E}_{i}} = \mathcal {H}_{q, Q_{a_{1}}, \dots , Q_{a_{j}}}$ if $\mathcal {E}_{i} = \{Q_{a_{1}}, \dots , Q_{a_{j}}\}$ . Since we are interested in irreducible, unitary representations, it is enough to restrict to a single direct summand on the right-hand side of equation (2.24).

It follows from the crystal-theoretic characterization of calibrated representations (see Theorem 4.4 below) that a representation $\bigotimes _{i = 1}^{k} M_{i}$ of $\bigotimes _{i = 1}^{k}\mathcal {H}_{q, \mathcal {E}_{i}}(n_{i})$ is calibrated if and only if each tensor factor $M_{i}$ is a calibrated representation of $\mathcal {H}_{q, \mathcal {E}_{i}}(n_{i})$ . Similarly, if $\bigotimes _{i = 1}^{k} M_{i}$ is unitary, then $M_{i}$ is a unitary representation of $\mathcal {H}_{q, \mathcal {E}_{i}}(n_{i})$ for every i. The converse, however, is not true. For example, in the most generic case when each equivalence class $\mathcal {E}_{i}$ consists of a single element, a representation

$$ \begin{align*}\bigotimes_{i = 1}^{k}D(\lambda_{i}) \in \bigotimes_{i = 1}^{k}\mathcal{H}_{q, Q_{i}}(n_{i})\operatorname{-mod} \end{align*} $$

is unitary if and only if $D(\lambda _{i})$ is a unitary representation of $\mathcal {H}_{q, Q_{i}}(n_{i}) \cong H_{q}(n_{i})$ and, for $i \neq j$ , $\Re (Q_{i}Q_{j}^{-1}q^{a-b}) \leq \Re (q)$ , where a ranges over the contents of all boxes in the partition $\lambda _{i}$ , and b ranges over the contents of all boxes in the partition $\lambda _{j}$ .

Since checking the condition on Remark 2.25 quickly becomes unwieldy when there are many pages, we will restrict our attention to cyclotomic Hecke algebras of the form stated in Lemma 2.23. We remark, however, that, thanks to the decomposition (2.24), many of the results we prove for unitary representations, including the construction of BGG resolutions, can be extended to the general setting. For a fixed parameter $q, Q_1, \dots , Q_{\ell }$ of the cyclotomic Hecke algebra, we will find all the $\ell $ -partitions labelling unitary representations. We define this set in Section 3 and prove that it indeed labels the unitary representations in Section 4.

3.1 The right border multiset of an $\ell $ -partition with respect to an $\ell $ -charge

We define the right border multiset $\mathsf {B}^{\mathbf {s}}({\boldsymbol {\lambda }})$ of ${\boldsymbol {\lambda }}$ with respect to the charge $\mathbf {s}$ to be the collection of integers $\mathsf {co}^{\mathbf {s}}(b)$ for each b the last box of a row of ${\boldsymbol {\lambda }}$ , with multiplicities. As in writing partitions, we will record right border multisets using exponential notation, that is, if ${\boldsymbol {\lambda }}$ has m rows whose last boxes b satisfy $\mathsf {co}^{\mathbf {s}}(b)=a$ , then we will write $\mathsf {B}^{\mathbf {s}}({\boldsymbol {\lambda }})=\{\ldots ,a^m,\ldots \}$ .

Example 3.1. Let $\ell =3$ , ${\boldsymbol {\lambda }}=((2^2),(2),(3,2))$ , and $\mathbf {s}=(0,1,4)$ . Then $\mathsf {B}^{\mathbf {s}}({\boldsymbol {\lambda }})=\{6,4,2,1,0\}$ (see Figure 2 for a visualisation). In this example, $\mathsf {B}^{\mathbf {s}}({\boldsymbol {\lambda }})$ is multiplicity-free.

Figure 2 The $3$ -partitions from Examples 3.1 and 3.2 together with their contents. We have highlighted the boxes at the end of each row in the Young diagram of ${\boldsymbol {\lambda }}$ .

If $\ell =1$ so that ${\boldsymbol {\lambda }}$ is a single partition $\lambda $ and $s\in \mathbb {Z}$ , then $\mathsf {B}^s(\lambda )$ is always multiplicity-free. However, for $\ell $ -partitions with $\ell>1$ this need not be the case as the next example shows.

We define the reading word of $\mathsf {B}^{\mathbf {s}}({\boldsymbol {\lambda }})$ to be the sequence of integers given by listing the elements of $\mathsf {B}^{s_1}(\lambda ^1)$ in increasing order, then the elements of $\mathsf {B}^{s_2}(\lambda ^2)$ in increasing order and so on. Thus, the reading word is a preferred order of listing the elements of $\mathsf {B}^{\mathbf {s}}({\boldsymbol {\lambda }})$ . Let $w=(a_1,a_2,\ldots ,a_h)$ be the reading word of $\mathsf {B}^{\mathbf {s}}({\boldsymbol {\lambda }})$ (here, h is the number of rows of ${\boldsymbol {\lambda }}$ ). We say that w is increasing if $a_1<a_2<\ldots <a_h$ . In Example 3.1, the reading word is $(0,1,2,4,6)$ and is increasing. In Example 3.2, the reading word is $(0,1,-1,1,2,2,4,6)$ and is not increasing.

3.2 The set $\mathsf {Cali}^{\mathbf {s}}(\ell )$

We now define a set of multipartitions that, as we will see below in Theorem 4.5, provides a combinatorial description of the calibrated irreducible representations of an appropriate cyclotomic Hecke algebra.

It is immediate that ${\boldsymbol {\lambda }}\in \mathsf {Cali}^{\mathbf {s}}(\ell )$ implies that ${\boldsymbol {\lambda }}$ is FLOTW; see Definition 1.16.

In the case that ${\boldsymbol {\lambda }}$ satisfies Definition 3.3(1), it is easy to check whether ${\boldsymbol {\lambda }}$ is cylindrical. Given ${\boldsymbol {\lambda }}=(\lambda ^1,\lambda ^2,\ldots ,\lambda ^{\ell })$ , if $\lambda ^j\neq \emptyset $ , then define $b^j_{\mathrm {min}}$ to be the box of smallest content in $\lambda ^j$ . That is, $b^j_{\mathrm {min}}$ is the leftmost box of the bottom row of $\lambda ^j$ . For each $j=1,\ldots ,\ell $ such that $\lambda ^j\neq \emptyset $ , let $h_j$ be the number of nonzero rows of $\lambda ^j$ . For $\lambda ^j\neq \emptyset $ , we have $\mathsf {co}^{\mathbf {s}}(b^j_{\mathrm {min}})=-h_j+1+s_j$ .

Proof. First, we show that any ${\boldsymbol {\lambda }}$ satisfying (1) and (2) is cylindrical. We have that (1) holds if and only if $-s_j>-\mathsf {co}^{\mathbf {s}}(b^{j+1}_{\mathrm {min}})=h_{j+1}-1-s_{j+1}$ , if and only if $s_{j+1}-s_j>h_{j+1}-1$ . Thus, (1) holds if and only if for all $k\geq 1$ we have $\lambda ^{j+1}_{k+s_{j+1}-s_j}=0$ , which is 1.16(2)(a). If $\lambda ^1=\emptyset $ , then it automatically holds that $\lambda _k^{\ell }\geq \lambda ^1_{k+e+s_1-s_{\ell }}$ for all $k\geq 1$ , that is, 1.16(2)(b) holds. So assume $\lambda ^1\neq \emptyset $ . Then (2) holds if and only if $s_{\ell }<-h_1+1+s_1+e$ if and only if $h_1<e+s_1-s_{\ell }$ , implying that $\lambda ^1_{k+e+s_1-s_{\ell }}=0$ for all $k\geq 1$ . Thus, 1.16(2)(b) holds.

For the converse, suppose that ${\boldsymbol {\lambda }} $ is cylindrical. Suppose $j\in \{1,\ldots ,\ell -1\}$ such that $\lambda ^{j+1}\neq \emptyset $ . To verify condition (1), we need to show that $h_{j+1}\leq s_{j+1}-s_j$ . Suppose not, then there exists $k\geq 1$ such that $h_{j+1}=s_{j+1}-s_j+k$ . Definition 1.16(2)(a) tells us that

$$ \begin{align*} \lambda_{h_{j+1}}^{j+1}=\lambda_{s_{j+1}-s_j+k}\leq \lambda_k^j\leq \lambda_1^j. \end{align*} $$

Since $\mathsf {B}^{\mathbf {s}}({\boldsymbol {\lambda }})$ is increasing, the charged content of the rightmost box of the bottom row of $\lambda ^{j+1}$ is greater than the charged content of the rightmost box of the top row of $\lambda ^j$ . This yields the inequality:

$$ \begin{align*} \lambda^j_1+s_j-1<\lambda^{j+1}_{h_{j+1}}+s_{j+1}-h_{j+1}=\lambda^{j+1}_{h_{j+1}}+s_{j+1}-(s_{j+1}-s_j+k)\leq \lambda^{j+1}_{h_{j+1}}+s_j-1 \end{align*} $$

giving $\lambda _1^j<\lambda _{h_{j+1}}^{j+1}$ , a contradiction.

Next, we verify condition (2) by a similar argument. If $\lambda ^1=\emptyset $ , then using that $\mathbf {s}$ is cylindrical together with condition (1) that was just proved, we have $s_{\ell }<s_1+e\leq s_{j-1}+e<\mathsf {co}^{\mathbf {s}}(b^j_{\mathrm {min}})+e$ , where $j\geq 2$ is minimal such that $\lambda ^j\neq \emptyset $ . So we can assume $j=1$ , that is, $\lambda ^1\neq \emptyset $ . We want to show that $s_{\ell }<\mathsf {co}^{\mathbf {s}}(b^1_{\mathrm {min}})$ . We have $\mathsf {co}^{\mathbf {s}}(b^1_{\mathrm {min}})=-h_1+1+s_1+e$ , so we need to show that $h_1\leq s_1-s_{\ell }+e$ . Suppose not, then we can write $h_1=s_1-s_{\ell }+e+k$ for some $k\geq 1$ . By the assumption that ${\boldsymbol {\lambda }}$ is FLOTW, we have $\lambda ^{\ell }_1\geq \lambda ^1_{1+e+s_1-s_{\ell }}\geq \lambda ^1_{h_1}>0$ . Thus, $\lambda ^{\ell }\neq \emptyset $ . On the other hand, by the assumption that ${\boldsymbol {\lambda }}$ satisfies Definition 3.3(1), it holds that the largest element of $\mathsf {B}^{\mathbf {s}}({\boldsymbol {\lambda }})$ is less than the smallest element of $\mathsf {B}^{\mathbf {s}}({\boldsymbol {\lambda }})$ plus e. Thus, $\lambda ^{\ell }_1+s_{\ell }-1<\lambda ^1_{h_1}-h_1+s_1+e$ . But $\lambda ^1_{h_1}-h_1+s_1+e=\lambda ^1_{h_1}-(s_1-s_{\ell }+e+k)+s_1+e=\lambda ^1_{h_1}+s_{\ell }-k\leq \lambda ^1_{h_1}+s_{\ell }-1$ . So we get $\lambda ^{\ell }_1<\lambda ^1_{h_1}$ , a contradiction with $\lambda ^{\ell }_1\geq \lambda ^1_{h_1}$ that followed above from ${\boldsymbol {\lambda }}$ being FLOTW. This concludes the proof.

3.3 Multiplicity-free right border sets and semi-infinite Young diagrams

Let $\mathcal {I}\subset \mathbb {Z}$ be a finite subset of the integers. Write $\mathcal {I}=\{i_h<i_{h-1}<\ldots <i_2<i_1\}$ . We define the semi-infinite Young diagram with right border set $\mathcal {I}$ to be the set of boxes $b=(x,y)$ , $1\leq x\leq h$ and $y \leq i_{x}+x$ , and we denote it by $\widetilde {Y}(\mathcal {I})$ . We will think of x as the row and y as the column and will draw the rows as descending as in our convention for ordinary Young diagrams. The content of a box $b=(x,y)\in \widetilde {Y}(\mathcal {I})$ is $\mathsf {co}^{\mathcal {I}}(b):=y-x$ .

Example 3.7. Suppose $\mathcal {I}=\{0,1,2,4,6\} $ . This determines $\widetilde {Y}(\mathcal {I})$ as in the leftmost diagram in Figure 3. Truncating at the column whose topmost box has content $0$ , we obtain the Young diagram of $\lambda =(7,6,5^3)$ with charge $0$ as depicted in the rightmost diagram in Figure 3.

Figure 3 The diagram $\widetilde {Y}(\mathcal {I})$ as in Example 3.7 and its truncation at the column whose topmost box has content $0$ to obtain the Young diagram of $\lambda =(7,6,5^3)$ .

Fix $\mathcal {I}=\{i_1,\ldots ,i_h\}\subset \mathbb {Z}$ and some $e\in \mathbb {N}$ such that $e>i_1-i_h$ and $e>h$ . In Example 3.7, we may take any $e\geq 7$ . For any $\ell \geq 1$ , we will construct a particular set of charged $\ell $ -partitions ${\boldsymbol {\lambda }}$ with cylindrical charge $\mathbf {s}$ and such that $\mathsf {B}^{\mathbf {s}}({\boldsymbol {\lambda }})=\mathcal {I}$ . First, we choose $s_1\in \mathbb {Z}$ such that $s_1\leq i_h$ . Then, we choose a box $b_1=(x_1,y_1)\in \widetilde {Y}(\mathcal {I})$ such that $\mathsf {co}^{\mathcal {I}}(b)=s_1$ . Thus, $b_1$ lies on or to the left of the northwest-southeast diagonal ending at the bottom-right box of the diagram $\widetilde {Y}(\mathcal {I})$ . The box $b_1$ will be the top left corner of $\lambda ^1$ . We then take $\lambda ^1$ to be the partition consisting of all boxes in $\widetilde {Y}(\mathcal {I})$ below and to the right of $b_1$ . That is:

$$ \begin{align*} \lambda^1=\{b=(x,y)\in\widetilde{Y}(\mathcal{I})\mid x\geq x_1,\;y\geq y_1\}. \end{align*} $$

We then mark the boxes in $\widetilde {Y}(\mathcal {I})$ of content $\alpha $ , where $\alpha =\mathsf {co}^{s_1}(b^1_{\mathrm {min}})$ . Here, $b^1_{\mathrm {min}}$ is the bottom-leftmost box of $\lambda ^1$ , its box of smallest content. A choice of $s_1$ and $b_1$ is illustrated schematically in Figure 4 below, with $i_h$ and $\alpha $ also indicated.

Figure 4 Illustration of the first step of producing a calibrated multipartition from a semi-infinite Young diagram.

If $b_1$ is in the top row of $\widetilde {Y}(\mathcal {I})$ , then we stop here: We have constructed a charged $1$ -partition with right border $\mathcal {I}$ as above. Otherwise, we go to the next step. We choose some $s_2$ such that $s_1<s_2<\alpha +e$ . Observe that since $\widetilde {Y}(\mathcal {I})$ has less than e rows, this is always possible. On the diagonal of boxes with content $s_2$ , we pick a box $b_2=(x_2,y_2)$ such that $\mathsf {co}(b_2)=s_2$ , $x_2<x_1$ , and $y_2\geq y_1$ . If $s_2=\alpha +e-1$ , then we require that $x_2=1$ , that is, that $b_2$ is in the top row. We then take the partition $\lambda ^2$ to consist of those boxes of $\widetilde {Y}(\mathcal {I})$ lying below and right of $b_2$ and strictly above $\lambda ^1$ :

$$ \begin{align*} \lambda^2=\{b=(x,y)\in\widetilde{Y}(\mathcal{I})\mid x_2\leq x<x_1,\;y\geq y_2\}. \end{align*} $$

If $x_2\neq 1$ , that is, if $b_2$ is not in the top row of the diagram, then we continue the process with step 3 choosing $s_3$ and $\lambda ^3$ …At step i of this process, which occurs if $b_{i-1}$ is not in the top row of $\widetilde {Y}(\mathcal {I})$ , we choose $s_i$ such that $s_{i-1}<s_i<\alpha +e$ , and we choose $b_i=(x_i,y_i)\in \widetilde {Y}(\mathcal {I})$ satisfying $\mathsf {co}(b_i)=s_i$ , $x_i<x_{i-1}$ , and $y_i\geq y_{i-1}$ . We require that $x_i=1$ if $s_i=\alpha +e-1$ . We then define $\lambda ^i$ as

$$ \begin{align*} \lambda^i=\{b=(x,y)\in\widetilde{Y}(\mathcal{I})\mid x_i\leq x<x_{i-1},\;y\geq y_i\}. \end{align*} $$

The process terminates after $\ell \leq h$ steps since $\widetilde {Y}(\mathcal {I})$ has h rows, and each step chooses a box $b_i$ in a row above the row containing $b_{i-1}$ . We take ${\boldsymbol {\lambda }}=(\lambda ^1,\lambda ^2,\ldots ,\lambda ^{\ell })$ and $\mathbf {s}=(s_1,s_2,\ldots ,s_{\ell })$ . Then $\mathbf {s}$ satisfies $s_1<s_2<\ldots <s_{\ell }<\alpha +e \leq s_1+e$ so is cylindric, and each $\lambda ^j$ is nonempty, $1\leq j\leq \ell $ .

The result of constructing $({\color {SpringGreen}\lambda ^1},{\color {Melon}\lambda ^2},{\color {Thistle}\lambda ^3},\ldots ,{\color {SkyBlue}\lambda ^{\ell }}),({\color {SpringGreen}s_1},{\color {Melon}s_2},{\color {Thistle}s_3},\ldots ,{\color {SkyBlue}s_{\ell }})$ for $\ell =4$ from the semi-infinite Young diagram of some $\mathcal {I}=\{i_1,\ldots ,i_h\}\subset \mathbb {Z}$ is depicted schematically in Figure 5 below. The partitions must be stacked in such a way that they make a staircase shape.

Figure 5 Constructing a charged $4$ -partition in $\mathsf {Cali}^{\mathbf {s}}(4)$ with a given border set $\{i_1,i_2,i_3,\ldots ,i_h\}$ .

For ${\boldsymbol {\lambda }}\in \mathsf {Cali}^{\mathbf {s}}(\ell )$ , removing all empty components $\lambda ^j=\emptyset $ yields a charged m-partition obtained from $\widetilde {Y}(\mathcal {I})$ by the procedure of Section 3.3 with $\mathcal {I}=\mathsf {B}^{\mathbf {s}}({\boldsymbol {\lambda }})$ and where $m=\ell -\#\{\lambda ^j=\emptyset \}$ . Conversely, for a given $\mathcal {I}\subset \mathbb {Z}$ such that $\mathcal {I}\subset [z,z+e-1]$ for some z and $|\mathcal {I}|<e$ , we can start from some ${\boldsymbol {\lambda }}\in \mathsf {Cali}^{\mathbf {s}}(\ell )$ produced from $\widetilde {Y}(\mathcal {I})$ , then insert empty components to obtain some $\boldsymbol {\mu }\in \mathsf {Cali}^{\mathbf {s}'}(\ell ')$ , $\ell '>\ell $ , with cylindrical charge $\mathbf {s}'\in \mathbb {Z}^{\ell '}$ such that $\{s_1,\ldots ,s_{\ell }\}\subset \{s_{1^{\prime }},\ldots ,s_{{\ell }^{\prime \prime }}\}$ . The components of the charge for the empty components must be chosen so that the $\ell '$ -partition remains cylindrical, that is, by respecting the conditions in Lemma 3.4.

Example 3.8. Let $\ell =3$ , $\mathbf {s}=(0,1,4)$ and ${\boldsymbol {\lambda }}=((2^2),(2),(3,2))$ as in Example 3.1. Suppose $e\geq 7$ . Then ${\boldsymbol {\lambda }}\in \mathsf {Cali}^{\mathbf {s}}(3)$ , as was shown in Example 3.6. We can construct ${\boldsymbol {\lambda }}$ with charge $\mathbf {s}$ from $\widetilde {Y}(\{0,1,2,4,6\})$ as depicted in Figure 6. Then by inserting empty components following the conditions of Lemma 3.4 on their charges, we can, for example, obtain a $6$ -partition $\boldsymbol {\mu }\in \mathsf {Cali}^{\mathbf {s}'}(6)$ having three nonempty components by taking $\mathbf {s}'=(-2,0,1,2,2,4)$ and $\boldsymbol {\mu }=(\emptyset , (2^2),(2),\emptyset ,\emptyset ,(3,2))$ .

Figure 6 Realizing ${\boldsymbol {\lambda }}=((2^2),(2),(3,2))\in \mathsf {Cali}^{(0,1,4)}(3)$ inside the semi-infinite Young diagram associated to its border set $\{0,1,2,4,6\}$ .

More generally, suppose that, upon removing all empty components from a charged $\ell $ -partition ${\boldsymbol {\lambda }}$ with some $\ell $ -charge $\mathbf {s}$ for some $\ell \geq 3$ , we get the $3$ -partition $((2^2),(2),(3,2))$ with charge $(0,1,4)$ as pictured above. Then ${\boldsymbol {\lambda }}\in \mathsf {Cali}^{\mathbf {s}}(\ell )$ if and only if ${\boldsymbol {\lambda }}=(\emptyset ^{a_{-2}},(2^2),\emptyset ^{a_0},(2),\emptyset ^{a_1+a_2},(3,2),\emptyset ^{a_4},\emptyset ^{a_5})$ and $\mathbf {s}=(-2^{a_{-2}},0^{1+a_0},1^{1+a_1},2^{a_2},4^{1+a_4},5^{a_5})$ for some $a_{-2},a_0,a_1,a_2,a_4,a_5\in \mathbb {Z}_{\geq 0}$ , where $a_5$ and $a_{-2}$ cannot both be nonzero. Here, we have used exponential notation. For example, taking $a_0=a_1=a_2=1$ , $a_5=2$ , and $a_4=a_{-2}=0$ we get that ${\boldsymbol {\lambda }}=((2^2),\emptyset ,(2),\emptyset ,\emptyset ,(3,2),\emptyset ,\emptyset )\in \mathsf {Cali}^{\mathbf {s}}(8)$ for $\mathbf {s}=(0,0,1,1,2,4,5,5)$ .

3.4 Skew shapes

From now on, when we talk about the Young diagram of ${\boldsymbol {\lambda }}\in \mathsf {Cali}^{\mathbf {s}}(\ell )$ , we will mean the embedding of the Young diagram of ${\boldsymbol {\lambda }}$ in $\widetilde {Y}(\mathsf {B}^{\mathbf {s}}({\boldsymbol {\lambda }}))$ given by stacking the $\lambda ^j$ ’s so that their right borders make up the right border of $\widetilde {Y}(\mathsf {B}^{\mathbf {s}}({\boldsymbol {\lambda }}))$ . We now jettison the semi-infinite blank region to the left of the $\lambda ^j$ ’s to obtain a diagram as in the leftmost depicted in Figure 7.

Figure 7 The diagram for ${\boldsymbol {\lambda }}=((2^2),(2),(3,2))$ for $\mathbf {s} = (0,1,4)$ and the skew-shape obtained by ‘forgetting components’.

Suppose ${\boldsymbol {\lambda }}\in \mathsf {Cali}^{\mathbf {s}}(\ell )$ . If we ‘forget components’ in its Young diagram $\mathsf {Y}^{\mathbf {s}}({\boldsymbol {\lambda }})$ , we get a skew partition. In the picture of the Young diagram of the charged $3$ -partition above, simply forget the different colors. In Example 3.8, the skew partition associated to $\mathsf {Y}^{\mathbf {s}}({\boldsymbol {\lambda }})$ has a Young diagram given by the region shown in the rightmost diagram in Figure 7 (remembering the contents of the boxes).

Suppose that every component $\lambda ^j$ of ${\boldsymbol {\lambda }}$ is nonempty. Then we may interpret Definition 3.3 as saying that when we express $\mathsf {Y}^{\mathbf {s}}({\boldsymbol {\lambda }})$ as $\mu \setminus \nu $ for some partitions $\mu $ and $\nu $ , then $\mu $ and $\nu $ both belong to $\mathsf {Cali}(1)$ . By [Reference Ruff50], $\mu \in \mathsf {Cali}(1)$ if and only if the irreducible representation $S_{\mu }$ of the finite Hecke algebra $H_q(S_n)$ for $q=\exp (2\pi i/e)$ is calibrated. By [Reference Ram45], the calibrated representations of the affine Hecke algebra $\widetilde {H}_q(S_n)$ for generic values of q are labelled by skew Young diagrams $\mu \setminus \nu $ . The condition for an $\ell $ -partition to be in ${\boldsymbol {\lambda }}\in \mathsf {Cali}^{\mathbf {s}}(\ell )$ thus arises as the intersection of two combinatorial conditions: on the one hand, the skew shape condition identifying calibrated representations of the affine type A Hecke algebra for q not a root of unity; and on the other hand, the condition identifying calibrated representations of the finite type A Hecke algebra for $q=\exp (2\pi i/e)$ , applied to the left and right borders of the skew shape. Now, if we further allow ${\boldsymbol {\lambda }}$ to contain empty components $\lambda ^j=\emptyset $ , then we just need to fine tune this description by the conditions on the charges of these empty components given by Definition 1.16 and Lemma 3.4. These extra conditions on where the empty components may occur and with what charge make sure that the resulting charge $\mathbf {s}$ and $\ell $ -partition ${\boldsymbol {\lambda }}$ remain cylindrical.

Remark 3.10. We remark that a single skew diagram can often be broken into many different charged multipartitions in an intuitive fashion. This is illustrated in Figure 8.

Figure 8 The eight possible ways of breaking a fixed skew shape into charged multipartitions with cylindric charge. The first two are ${\boldsymbol {\lambda }}=( (2^3),(3,2))$ for $\mathbf {s} = (1,4)$ and ${\boldsymbol {\lambda }}=( (2^2),(2), (3,2))$ for $\mathbf {s} = (0,1,4)$ . The rest are left for the reader. Notice that the multipartitions all have $2\leq \ell \leq 5$ components.

To finish this section, we relate our constructions to the crystal operators $\tilde {e}_{i}$ of Section 1.2.

4.1 Irreducible representations of cyclotomic Hecke algebras at roots of unity

Recall that the cyclotomic Hecke algebra (or Ariki–Koike algebra) is the following quotient of the affine Hecke algebra:

$$ \begin{align*}\mathcal{H}_{q, Q_1, \dots, Q_{\ell}}(n) = \frac{\mathcal{H}_{q}^{\operatorname{\mathrm{aff}}}(n)}{(\prod_{i = 1}^{\ell}X_{1} - Q_{i})}. \end{align*} $$

Fix $e\geq 2$ , $\ell \geq 1$ , and $\mathbf {s}\in \mathbb {Z}^{\ell }$ . Set $q=\exp (2\pi i/e)$ and $Q_i=q^{s_i}$ . For such a choice of parameters (sometimes called ‘integral parameters’ in the literature), we will denote $\mathcal {H}_{q, Q_1, \dots , Q_{\ell }}(n)$ by $\mathcal {H}_{e,\mathbf {s}}(n)$ .

In the case that $\mathbf {s}$ is a cylindrical charge (see Definition 1.1), Foda, Leclerc, Okado, Thibon and Welsh gave a closed-form description of these $\ell $ -partitions. Recall the definition of the set of FLOTW $\ell $ -partitions (Definition 1.16).

The goal of this section is to give the analogous closed-form description of the $\ell $ -partitions labelling the irreducible calibrated representations of $\mathcal {H}_{e,\mathbf {s}}(n) $ by the set of $\ell $ -partitions $\mathsf {Cali}^{\mathbf {s}}(\ell )$ (see Definition 3.3). First, we will need the following lemma, which uses Theorem 4.2.

The analogue of Theorem 4.1 for the irreducible calibrated representations of $\mathcal {H}_{e,\mathbf {s}}(n) $ identifies the $\ell $ -partitions labelling them in terms of certain paths in the $\widehat {\mathfrak {sl}}_e$ -crystal.

That is, we consider all possible ways to build up a FLOTW $\ell $ -partition ${\boldsymbol {\lambda }}$ from the empty $\ell $ -partition $\varnothing $ by adding one box at a time such that, at each step, the box we add is the good addable box for its residue. The theorem says that if ${\boldsymbol {\lambda }}$ labels an irreducible calibrated representation, then in all such sequences building up ${\boldsymbol {\lambda }}$ one box at a time, we never add an i-box immediately followed by another i-box.

We now arrive at the main result of this section, which is the analog of Theorem 4.2 for calibrated representations.

Proof. We will prove the statement by induction on n. The base case is $n=1$ . By Theorem 4.4, if $|{\boldsymbol {\lambda }}|=1$ , then ${\boldsymbol {\lambda }}$ labels an irreducible calibrated representation if and only if ${\boldsymbol {\lambda }}$ is FLOTW. By Definition 1.16 and Lemma 3.4, if $|{\boldsymbol {\lambda }}|=1$ , then ${\boldsymbol {\lambda }}\in \mathsf {Cali}^{\mathbf {s}}(\ell )$ if and only if ${\boldsymbol {\lambda }}$ is FLOTW.

Now, suppose by induction that, for all FLOTW $\ell $ -partitions ${\boldsymbol {\lambda }}$ of n, it holds that ${\boldsymbol {\lambda }}$ labels an irreducible calibrated representation of $\mathcal {H}_{e,\mathbf {s}}(n)$ if and only if ${\boldsymbol {\lambda }}\in \mathsf {Cali}^{\mathbf {s}}(\ell )$ .

First, we will show that any $\ell $ -partition of size $n+1$ in $\mathsf {Cali}^{\mathbf {s}}(\ell )$ labels an irreducible calibrated representation of $\mathcal {H}_{e,\mathbf {s}}(n+1)$ . Suppose that $\boldsymbol {\mu }\in \mathsf {Cali}^{\mathbf {s}}(\ell )$ and $|\boldsymbol {\mu }|=n+1$ . Then $\boldsymbol {\mu }$ is FLOTW, so by Theorems 4.1 and 4.2, $\boldsymbol {\mu }=\tilde {f}_{i_{n+1}}\tilde {f}_{i_n}\ldots \tilde {f}_{i_2}\tilde {f}_{i_1}\varnothing $ for some $i_1,\ldots ,i_{n+1}\in \mathbb {Z}/e\mathbb {Z}$ . We must show that every such expression satisfies $i_k\neq i_{k+1}$ for each $k=1,\ldots , n$ . Let $i\in \mathbb {Z}/e\mathbb {Z}$ such that $\tilde {e}_i(\boldsymbol {\mu })\neq 0$ . By Lemma 4.3, $\tilde {e}_i\boldsymbol {\mu }\in \mathsf {Cali}^{\mathbf {s}}(\ell )$ . By induction, every expression $\tilde {e}_i\boldsymbol {\mu }=\tilde {f}_{i_{n}}\ldots \tilde {f}_{i_2}\tilde {f}_{i_1}\varnothing $ satisfies $i_k\neq i_{k+1}$ for all $k=1,\ldots ,n-1$ . It thus suffices to check that $i_n\neq i$ . The charged contents of removable boxes of $\boldsymbol {\mu }$ belong to $\mathsf {B}^{\mathbf {s}}(\boldsymbol {\mu })$ . By Definition 3.3, $\mathsf {B}^{\mathbf {s}}(\boldsymbol {\mu })$ contains at most one element of residue i mod e, so $\boldsymbol {\mu }$ has at most one removable i-box. It follows that $\tilde {e}_i\boldsymbol {\mu }$ has no removable i-box. Therefore, $\tilde {e}_i\tilde {e}_i\boldsymbol {\mu }=0$ , implying $i_n\neq i$ . We conclude using Theorem 4.4 that $\boldsymbol {\mu }$ labels an irreducible calibrated representation of $\mathcal {H}_{e,\mathbf {s}}(n+1)$ .

The remainder of the proof is dedicated to showing that if ${\boldsymbol {\lambda }}$ is a FLOTW $\ell $ -partition of size $n+1$ that labels an irreducible calibrated representation of $\mathcal {H}_{e,\mathbf {s}}(n+1)$ , then ${\boldsymbol {\lambda }}\in \mathsf {Cali}^{\mathbf {s}}(\ell )$ . Suppose that $\boldsymbol {\mu }$ is FLOTW, $|\boldsymbol {\mu }|=n+1$ , and $\boldsymbol {\mu }$ labels an irreducible calibrated representation. By Theorem 4.4, for every expression $\boldsymbol {\mu }=\tilde {f}_{i_{n+1}}\tilde {f}_{i_n}\ldots \tilde {f}_{i_2}\tilde {f}_{i_1}\varnothing $ it holds that $i_{k+1}\neq i_k$ for all $k=1,\ldots ,n$ . We need to show that $\boldsymbol {\mu }$ satisfies Definition 3.3(1). By induction, $\boldsymbol {\mu }=\tilde {f}_i{\boldsymbol {\lambda }}$ for some ${\boldsymbol {\lambda }}\in \mathsf {Cali}^{\mathbf {s}}(\ell )$ and some $i\in \mathbb {Z}/e\mathbb {Z}$ . Either $\tilde {f}_i$ adds a box to a nonzero row of ${\boldsymbol {\lambda }}$ , or $\tilde {f}_i$ creates a new row. In the case that $\tilde {f}_i$ adds a box to an already existing row, the result is forced by the induction hypothesis that ${\boldsymbol {\lambda }}\in \mathsf {Cali}^{\mathbf {s}}(\ell )$ using arguments similar to those in the proof of Lemma 3.11. This is straightforward to check. The work consists in dealing with the case that $\tilde {f}_i$ adds the good i-box in a new row of ${\boldsymbol {\lambda }}$ . Thus, we suppose from now on that $\tilde {f}_i$ adds a new row to ${\boldsymbol {\lambda }}$ , that is, that $|\mathsf {B}^{\mathbf {s}}(\boldsymbol {\mu })|=|\mathsf {B}^{\mathbf {s}}({\boldsymbol {\lambda }})|+1$ . We will show that if Definition 3.3(1)(a) or Definition 3.3(1)(b) fails for $\tilde {f}_i{\boldsymbol {\lambda }}=\boldsymbol {\mu }$ , then there exists an expression $\tilde {f}_{i_{n+1}}\tilde {f}_{i_n}\ldots \tilde {f}_{i_2}\tilde {f}_{i_1}\varnothing =\boldsymbol {\mu }$ with $i_k=i=i_{k+1}$ for some $k\in \{1,\ldots ,n\}$ .

First, suppose Definition 3.3(1)(a) fails, so suppose $\mathsf {B}^{\mathbf {s}}(\boldsymbol {\mu })\not \subset [z,z+e-1]$ for all $z\in \mathbb {Z}$ . Let b be the i-box added by $\tilde {f}_i$ to ${\boldsymbol {\lambda }}$ , that is, $\boldsymbol {\mu }=\tilde {f}_i{\boldsymbol {\lambda }}\cup \{b\}$ , and let $j(b)\in \{1,\ldots ,\ell \}$ be such that b is a box in $\mu ^{j(b)}$ . First, we show that $\mathsf {co}^{\mathbf {s}}(b)$ must be the smallest element of $\mathsf {B}^{\mathbf {s}}(\boldsymbol {\mu })$ . Suppose that $\mathsf {co}^{\mathbf {s}}(b)$ is neither the smallest nor the largest element of $\mathsf {B}^{\mathbf {s}}(\boldsymbol {\mu })$ . Since $\mathsf {B}^{\mathbf {s}}({\boldsymbol {\lambda }})\subset [z,z+e-1]$ for some $z\in \mathbb {Z}$ , this implies that $\mathsf {B}^{\mathbf {s}}(\boldsymbol {\mu })=[z,z+e-1]$ for some $z\in \mathbb {Z}$ , and thus $\mathsf {co}^{\mathbf {s}}(b)-1\in \mathsf {B}^{\mathbf {s}}({\boldsymbol {\lambda }})$ . Then $\mathsf {co}^{\mathbf {s}}(b)-1$ is the content of the box of largest content in $\mu ^k$ for some $k<j(b)$ . But then $\mu ^k$ has an addable box of content $\mathsf {co}^{\mathbf {s}}(b)$ . It follows that the good addable box of ${\boldsymbol {\lambda }}$ is then in $\mu ^k$ , not in $\mu ^{j(b)}$ , contradicting the assumption. Next, since ${\boldsymbol {\lambda }}\in \mathsf {Cali}^{\mathbf {s}}(\ell )$ , then by Lemma 3.4 we have $s_{j(b)}-\mathsf {co}^{\mathbf {s}}(b_{\mathrm {min}})< e$ , where $b_{\mathrm {min}}$ is the box of smallest charged content in ${\boldsymbol {\lambda }}$ . Thus, if $\mathsf {co}^{\mathbf {s}}(b)$ is the largest element of $\mathsf {B}^{\mathbf {s}}(\boldsymbol {\mu })$ , then $\mathsf {B}^{\mathbf {s}}(\boldsymbol {\mu })\subseteq [z,z+e-1]$ and we repeat the argument above to get a contradiction. We conclude that $\mathsf {co}^{\mathbf {s}}(b)$ the smallest element of $\mathsf {B}^{\mathbf {s}}(\boldsymbol {\mu })$ , and moreover (again by the same argument), $\mathsf {co}^{\mathbf {s}}(b)\neq \mathsf {co}^{\mathbf {s}}(b_{\mathrm {max}})-e+1$ .

It follows that there exists a unique $w\in \mathbb {Z}$ such that $w=\mathsf {co}^{\mathbf {s}}(b)+qe$ for some positive integer q, $w-e<x<w+e$ for all $x\in \mathsf {B}^{\mathbf {s}}({\boldsymbol {\lambda }})=\mathsf {B}^{\mathbf {s}}(\boldsymbol {\mu })\setminus \{\mathsf {co}^{\mathbf {s}}(b)\}$ , and there is some $x\in \mathsf {B}^{\mathbf {s}}({\boldsymbol {\lambda }})$ with $x\geq w$ . We observe that ${\boldsymbol {\lambda }}$ cannot have an addable box of content w in one of its nonzero rows, for if it did, then $\tilde {e}_i$ would have added this box rather than b. Thus, if $w-1\in \mathsf {B}^{\mathbf {s}}(\boldsymbol {\mu })$ , it must also hold that $w\in \mathsf {B}^{\mathbf {s}}(\boldsymbol {\mu })$ .

Step 1. Case (i). Suppose $w-1\notin \mathsf {B}^{\mathbf {s}}(\boldsymbol {\mu })$ . Consider $\mathsf {B}^{\mathbf {s}}(\boldsymbol {\mu })\cap \mathbb {Z}_{\geq w}$ , and the corresponding boxes in the right border of $\boldsymbol {\mu }$ that are of charged content at least w. Let $r=|\mathsf {B}^{\mathbf {s}}(\boldsymbol {\mu })\cap \mathbb {Z}_{\geq w}|$ . Since the reading word of $\mathsf {B}^{\mathbf {s}}({\boldsymbol {\lambda }})$ is increasing, these boxes belong to the top r rows of $\mathsf {Y}^{\mathbf {s}}({\boldsymbol {\lambda }})$ . We have $0<r\leq e-1$ . If $\mathsf {B}^{\mathbf {s}}(\boldsymbol {\mu })\cap \mathbb {Z}_{\geq w}=[w,w+r-1]$ , proceed to step 2. Otherwise, let y be the minimal element of $\mathsf {B}^{\mathbf {s}}(\boldsymbol {\mu })\cap \mathbb {Z}_{\geq w}$ . Apply $\tilde {e}:=\tilde {e}_{i+1}\tilde {e}_{i+2}\ldots \tilde {e}_{y-1}\tilde {e}_y$ to $\boldsymbol {\mu }$ . This removes a horizontal strip of $y-w+1$ boxes from the r’th row of $\mathsf {Y}^{\mathbf {s}}(\boldsymbol {\mu })$ because $\boldsymbol {\mu }={\boldsymbol {\lambda }}\cup \{b\}$ has no addable boxes of these residues with charged content w or greater nor does it have any (other) removable boxes of these residues. Applying $\tilde {e}_i\tilde {e}_i$ to $\tilde {e}\boldsymbol {\mu }$ now removes b and the removable i-box in row r yielding $\boldsymbol {\nu }$ such that $\boldsymbol {\mu }=\tilde {f}_y\tilde {f}_{y-1}\ldots \tilde {f}_{i+2}\tilde {f}_{i+1}\tilde {f}_i\tilde {f}_i\boldsymbol {\nu }$ , a contradiction. This step of the proof is illustrated in Figure 9.

Figure 9 Illustration of the proof of Theorem 4.5, induction step verifying that failure of Definition 3.3(1)(a) implies failure to be calibrated. Step 1, case (i).

Step 1. Case (ii). Suppose $w-1\in \mathsf {B}^{\mathbf {s}}(\boldsymbol {\mu })$ . Let $w-e<x_t<\ldots <x_2<x_1<w$ be the elements of $\mathsf {B}^{\mathbf {s}}({\boldsymbol {\lambda }})\cap \mathbb {Z}_{<w}$ . If $x_1<w-1$ , proceed to step 2. Otherwise, let $h\in \{1,\ldots ,t\}$ be minimal such that $x_h-1\notin \mathsf {B}^{\mathbf {s}}({\boldsymbol {\lambda }})$ . If $x_h-1+e\notin \mathsf {B}^{\mathbf {s}}({\boldsymbol {\lambda }})$ , then set $\boldsymbol {\nu }=\tilde {e}_{i-1}\ldots \tilde {e}_{i-h}\boldsymbol {\mu }$ . In $\mathsf {Y}^{\mathbf {s}}({\boldsymbol {\lambda }})$ , this corresponds to removing a vertical strip consisting of the boxes lying in the same column and strictly below the box in row r of content w. If $x_h-1+e\in \mathsf {B}^{\mathbf {s}}({\boldsymbol {\lambda }})$ (which can only happen if $x_h$ is the minimal element of $\mathsf {B}^{\mathbf {s}}({\boldsymbol {\lambda }})$ and $x_h-1+e$ is the maximal element of $\mathsf {B}^{\mathbf {s}}({\boldsymbol {\lambda }})$ ), apply the procedure in case (i) to obtain $\boldsymbol {\nu }_1$ from $\boldsymbol {\mu }$ such that $\mathsf {B}^{\mathbf {s}}(\boldsymbol {\nu }_1)\cap \mathbb {Z}_{\geq w}=[w,w+r-1]$ , and then set $\boldsymbol {\nu }=\tilde {e}_{i-1}\ldots \tilde {e}_{i-h}\boldsymbol {\nu }_1$ . Since $w-1\in \mathsf {B}^{\mathbf {s}}(\boldsymbol {\mu })$ forced $w\in \mathsf {B}^{\mathbf {s}}(\boldsymbol {\mu })$ as well, we obtain $\boldsymbol {\nu }$ with $w\in \mathsf {B}^{\mathbf {s}}(\boldsymbol {\nu })$ and $w-1\notin \mathsf {B}^{\mathbf {s}}(\boldsymbol {\nu })$ .

Step 2. Recall that $w\cong \mathsf {co}^{\mathbf {s}}(b)\cong i \mod e$ . The $\ell $ -partition $\boldsymbol {\nu }$ has no addable i-box in any of its nonzero rows. It has two removable i-boxes: b and the box of content w in its border. Since $\tilde {f}_i$ added the box $\mathsf {co}^{\mathbf {s}}(b)$ to ${\boldsymbol {\lambda }}$ , $\boldsymbol {\nu }$ has no addable i-box bigger than b in an empty row. The i-word for $\boldsymbol {\nu }$ is thus some number of plusses followed by $--$ . It follows that $\tilde {e}_i\tilde {e}_i$ removes the boxes of charged contents w and $\mathsf {co}^{\mathbf {s}}(b)$ from $\boldsymbol {\nu }$ . This shows that $\boldsymbol {\mu }= \tilde {f}_i\tilde {f}_i(\tilde {e}_i\tilde {e}_i\boldsymbol {\nu })$ , a contradiction with the assumption that $\boldsymbol {\mu }=\tilde {f}_i{\boldsymbol {\lambda }}$ labels a calibrated representation. Therefore, Definition 3.3(1)(a) must hold if $\tilde {f}_i{\boldsymbol {\lambda }}$ satisfies the condition of Theorem 4.4.

Finally, we suppose that $\tilde {f}_i{\boldsymbol {\lambda }}\neq 0$ satisfies the condition of Theorem 4.4 but that Definition 3.3(1)(b) fails for $\tilde {f}_i{\boldsymbol {\lambda }}$ . The argument by contradiction is similar to the one checking Definition 3.3(1)(a). Define b and $j(b)$ be as above. By assumption, the reading word of $\mathsf {B}^{\mathbf {s}}(\boldsymbol {\mu })$ is not increasing, but the reading word of $\mathsf {B}^{\mathbf {s}}({\boldsymbol {\lambda }})$ is. By the previous step of the proof, we know that the elements of $\mathsf {B}^{\mathbf {s}}(\boldsymbol {\mu })$ all belong to an interval $[z,z+e-1]$ for some $z\in \mathbb {Z}$ . Since we are in the case that adding b creates a new row in component $j(b)$ and $h({\boldsymbol {\lambda }})$ is $\mathbf {s}$ -admissible by Lemma 3.5, we have $\mathsf {co}^{\mathbf {s}}(b)<\mathsf {co}^{\mathbf {s}}(b')$ for all $\mathsf {co}^{\mathbf {s}}(b')\in \mathsf {B}^{s_k}(\mu ^k)$ , $k\geq j(b)$ . Thus, there must exist a box $b'\in \mu ^m=\lambda ^m$ for some $m<j(b)$ such that $b'$ is the last box in its row and $\mathsf {co}^{\mathbf {s}}(b)\leq \mathsf {co}^{\mathbf {s}}(b')$ , and we take m to be minimal such that this happens. Now, we remove either a horizontal strip, a vertical strip or a combination of such from $\lambda ^m$ by crystal operators in order to arrive at a situation where $\tilde {e}_i$ can be applied twice in a row to get a nonzero $\ell $ -partition, as in the previous part of the proof. We arrive at that situation in the following ways depending on how the diagonal of charged content $\mathsf {co}^{\mathbf {s}}(b)$ intersects the Young diagram of $\lambda ^m$ in $\mathsf {Y}^{\mathbf {s}}({\boldsymbol {\lambda }})$ .

First, if $\mathsf {co}^{\mathbf {s}}(b)\leq \mathsf {co}^{\mathbf {s}}(b')$ for all boxes $b'$ the last in their rows in $\lambda ^m$ , then we remove all boxes of content larger than $\mathsf {co}^{\mathbf {s}}(b)$ from the bottom row of $\lambda ^m$ . We then have two removable boxes of residue i. These are successively good removable unless the largest element of $\mathsf {B}^{\mathbf {s}}({\boldsymbol {\lambda }})$ has residue $i-1$ . If the latter is the case, then we remove the topmost vertical strip in the border of $\mathsf {Y}^{\mathbf {s}}({\boldsymbol {\lambda }})$ . Then we may remove the two boxes of residue i by applying $\tilde {e}_i$ twice in a row.

Otherwise, i is the residue of a box in the right border ribbon of $\lambda ^m$ . We consider whether it occurs in an arm, a leg or a corner of this ribbon. We then remove, respectively, the arm to its right, the leg below it or the arm and the leg below it and to its right. In case the bottom box of the leg below it is the minimal element z of $\mathsf {B}^{\mathbf {s}}({\boldsymbol {\lambda }})$ and both $z,z+e-1\in \mathsf {B}^{\mathbf {s}}({\boldsymbol {\lambda }})$ , then again we have to remove the topmost vertical strip in the border of $\mathsf {Y}^{\mathbf {s}}({\boldsymbol {\lambda }})$ before we can remove that leg via crystal operators $\tilde {e}_j$ . We then arrive again at the situation that we may apply $\tilde {e}_i$ twice in a row to remove two boxes of residue i. Therefore, the irreducible representation labelled by $\boldsymbol {\mu }$ is not calibrated.