Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-09T16:19:10.778Z Has data issue: false hasContentIssue false
  • English
  • Français

THE UNIT MAP OF THE ALGEBRAIC SPECIAL LINEAR COBORDISM SPECTRUM

Part of: (Co)homology theory

Published online by Cambridge University Press:  24 December 2019

Maria Yakerson Open the ORCID record for Maria Yakerson [Opens in a new window]
Maria Yakerson*
Affiliation:
Fakultät für Mathematik, Universität Regensburg, Universitätstr. 31, 93040Regensburg, Germany ([email protected]) URL: https://www.muramatik.com
Get access Rights & Permissions [Opens in a new window]

Abstract

In the joint work with Elmanto, Hoyois, Khan and Sosnilo, we computed infinite 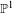$\mathbb{P}^{1}$-loop spaces of motivic Thom spectra using the technique of framed correspondences. This result allows us to express non-negative $\mathbb{G}_{m}$-homotopy groups of motivic Thom spectra in terms of geometric generators and relations. Using this explicit description, we show that the unit map of the algebraic special linear cobordism spectrum induces an isomorphism on 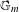$\mathbb{G}_{m}$-homotopy sheaves.

Keywords

framed correspondencesmotivic homotopy groups

MSC classification

Primary: 14F42: Motivic cohomology; motivic homotopy theory
Secondary: 14F99: None of the above, but in this section
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 6 , November 2021 , pp. 1905 - 1930
Check for updates
Copyright
© Cambridge University Press 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author was supported by SFB/TR 45 ‘Periods, moduli spaces and arithmetic of algebraic varieties’.

References

Ananyevskiy, A., Garkusha, G. and Panin, I., Cancellation theorem for framed motives of algebraic varieties, Preprint, 2018, arXiv:1601.06642v2.Google Scholar
Asok, A. and Haesemeyer, C., The 0-th stable $\mathbb{A}^{1}$ -homotopy sheaf and quadratic zero cycles, Preprint, 2011, arXiv:1108.3854v1.Google Scholar
Asok, A. and Morel, F., Smooth varieties up to 𝔸1 -homotopy and algebraic h-cobordisms, Adv. Math. 5(227) (2011), 1990–2058.Google Scholar
Bachmann, T., The generalized slices of Hermitian K-theory, J. Topol. 10(4) (2017), 1124–1144.Google Scholar
Bachmann, T. and Fasel, J., On the effectivity of spectra representing motivic cohomology theories, Preprint, 2018, arXiv:1710.00594v3.Google Scholar
Bachmann, T. and Hoyois, M., Norms in motivic homotopy theory, Preprint, 2018, arXiv:1711.03061v4.Google Scholar
Bachmann, T. and Hahn, J., Nilpotence in normed $\operatorname{MGL}$ -modules, Preprint, 2019, arXiv:1906.01306.Google Scholar
Calmès, B. and Fasel, J., The category of finite MW-correspondences, Preprint, 2017, arXiv:1412.2989v2.Google Scholar
Calmès, B. and Fasel, J., A comparison theorem for MW-motivic cohomology, Preprint, 2017, arXiv:1708.06100.Google Scholar
Déglise, F., Orientation theory in arithmetic geometry, Preprint, 2018, arXiv:1111.4203v3.Google Scholar
Déglise, F. and Fasel, J., $MW$ -motivic complexes, Preprint, 2017, arXiv:1708.06095.Google Scholar
Druzhinin, A. and Kylling, J., Framed correspondences and the zeroth stable motivic homotopy group in odd characteristic, Preprint, 2018, arXiv:1809.03238v2.Google Scholar
Druzhinin, A. and Panin, I., Surjectivity of the etale excision map for homotopy invariant framed presheaves, Preprint, 2018, arXiv:1808.07765v1.Google Scholar
Elmanto, E., Hoyois, M., Khan, A. A., Sosnilo, V. and Yakerson, M., Framed transfers and motivic fundamental classes, J. Topol. (2019), to appear in arXiv:1809.10666.Google Scholar
Elmanto, E., Hoyois, M., Khan, A. A., Sosnilo, V. and Yakerson, M., Modules over algebraic cobordism, Preprint, 2019, arXiv:1908.02162.Google Scholar
Elmanto, E., Hoyois, M., Khan, A. A., Sosnilo, V. and Yakerson, M., Motivic infinite loop spaces, Preprint, 2019, arXiv:1711.05248v5.Google Scholar
Gepner, D., Groth, M. and Nikolaus, T., Universality of multiplicative infinite loop space machines, Algebr. Geom. Topol. 15(6) (2015), 3107–3153.Google Scholar
Garkusha, G., Neshitov, A. and Panin, I., Framed motives of relative motivic spheres, Preprint, 2018, arXiv:1604.02732v3.Google Scholar
Garkusha, G. and Panin, I., Framed motives of algebraic varieties (after V. Voevodsky), Preprint, 2018, arXiv:1409.4372v4.Google Scholar
Garkusha, G. and Panin, I., Homotopy invariant presheaves with framed transfers, Preprint, 2018, arXiv:1504.00884v3.Google Scholar
Görtz, U. and Wedhorn, T., Algebraic Geometry I (Vieweg + Teubner, Wiesbaden, 2010).Google Scholar
Hoyois, M., From algebraic cobordism to motivic cohomology, J. Reine Angew. Math. 702 (2015), 173–226.Google Scholar
Hoyois, M., Cdh descent in equivariant homotopy $K$ -theory, Preprint, 2017, arXiv:1604.06410v3.Google Scholar
Levine, M., Toward an enumerative geometry with quadratic forms, Preprint, 2018, arXiv:1703.03049v3.Google Scholar
Morel, F., An introduction to 𝔸1 -homotopy theory, ICTP Trieste Lecture Note Ser. 15 (2003), 357–441.Google Scholar
Morel, F., 𝔸1 -Algebraic Topology over a Field, Lecture Notes in Mathematics, (Springer, Berlin Heidelberg, 2012).Google Scholar
Mazza, C., Voevodsky, V. and Weibel, C., Lecture Notes on Motivic Cohomology, Clay Mathematics Monographs, Volume 2 (American Mathematical Society, Providence, RI; Clay Mathematics Institute, Cambridge, MA, 2006).Google Scholar
Neshitov, A., Framed correspondences and the Milnor–Witt K-theory, J. Inst. Math. Jussieu 17(4) (2018), 823–852.Google Scholar
Panin, I. and Walter, C., On the algebraic cobordism spectra MSL and MSp, Preprint, 2010, arXiv:1011.0651.Google Scholar
Voevodsky, V., 𝔸1 -homotopy theory, Doc. Math., Extra Volume: Proceedings of the ICM I (1998), 579–604.Google Scholar
Voevodsky, V., Notes on framed correspondences, unpublished, 2001, http://www.math.ias.edu/vladimir/files/framed.pdf.Google Scholar
Yakerson, M., Motivic stable homotopy groups via framed correspondences, Ph.D. thesis, University of Duisburg-Essen, 2019, available at https://duepublico2.uni-due.de/receive/duepublico_mods_00070044?q=iakerson.Google Scholar