Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T09:38:07.000Z Has data issue: false hasContentIssue false
  • English
  • Français

Twisted geometric Satake equivalence

Part of: Lie groups Families, fibrations

Published online by Cambridge University Press:  24 March 2010

Michael Finkelberg  and
Sergey Lysenko
Michael Finkelberg
Affiliation:
Independent Moscow University, Institute for Information Transmission Problems and State University Higher School of Economy, Department of Mathematics, 20 Myasnitskaya Street, Moscow 101000, Russia ([email protected])
Sergey Lysenko
Affiliation:
Institut Élie Cartan Nancy (Mathématiques), Université Henri Poincaré Nancy 1, BP 70239, 54506 Vandoeuvre-lés-Nancy Cedex, France ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

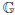Let k be an algebraically closed field and O = k[[t]] ⊂ F = k((t)). For an almost simple algebraic group G we classify central extensions 1 → m → E → G(F) → 1; any such extension splits canonically over G(O). Fix a positive integer N and a primitive character ζ : μN(K) → 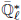(under some assumption on the characteristic of k). Consider the category of G(O)-bi-invariant perverse sheaves on E with 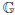m-monodromy ζ. We show that this is a tensor category, which is tensor equivalent to the category of representations of a reductive group ǦE,N. We compute the root datum of ǦE,N.

Keywords

geometric Langlands programSatake isomorphismmonodromic perverse sheaves

MSC classification

Secondary: 14D24: Geometric Langlands program 22E57: Geometric Langlands program
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 9 , Issue 4 , October 2010 , pp. 719 - 739
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Beilinson, A. and Drinfeld, V., Quantization of Hitchin's Hamiltonians and Hecke eigen-sheaves, preprint (available at www.math.uchicago.edu/~mitya/langlands.html).Google Scholar
2.Bourbaki, N., Groupes et algèbres de Lie, Chapter 6 (Hermann, Paris, 1968).Google Scholar
3.Brylinski, J.-L. and Deligne, P., Central extensions of reductive groups by K 2, Publ. Math. IHES 94 (2001), 5–85.CrossRefGoogle Scholar
4.Deligne, P. and Milne, J., Tannakian categories, in Hodge cycles, motives and Shimura varieties, Lecture Notes in Mathematics, Volume 900, pp. 101–228 (Springer, 1982).Google Scholar
5.Faltings, G., Algebraic loop groups and moduli spaces of bundles, J. Eur. Math. Soc. 5 (2003), 41–68.CrossRefGoogle Scholar
6.Gaitsgory, D., Twisted Whittaker model and factorizable sheaves, Selecta Math. 13 (2008), 617–659.CrossRefGoogle Scholar
7.Kapustin, A. and Witten, E., Electric–magnetic duality and the geometric Langlands program, Commun. Num. Theory Phys. 1 (2007), 1–236.CrossRefGoogle Scholar
8.Lusztig, G., Monodromic systems on affine flag manifolds, Proc. R. Soc. Lond. A 445 (1994), 231–246 (erratum: Proc. R. Soc. Lond. A 450 (1995), 731).Google Scholar
9.Lysenko, S., Moduli of metaplectic bundles on curves and theta-sheaves, Annales Scient. Éc. Norm. Sup. 39 (2006), 415–466.CrossRefGoogle Scholar
10.Mirković, I. and Vilonen, K., Geometric Langlands duality and representations of algebraic groups over commutative rings, Annals Math. (2) 166 (2007), 95–143.CrossRefGoogle Scholar
11.Savin, G., Local Shimura correspondence, Math. Annalen 280 (1988), 185–190.CrossRefGoogle Scholar