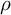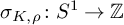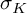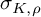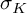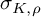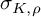1 Introduction
For a knot K, several invariants such as the Alexander polynomial
![]() $\Delta _K$
, the Levine–Tristram signature
$\Delta _K$
, the Levine–Tristram signature
![]() $\sigma _K \colon S^1 \to \mathbb {Z}$
and the Blanchfield form
$\sigma _K \colon S^1 \to \mathbb {Z}$
and the Blanchfield form
![]() $\operatorname {\mathrm {Bl}}(K)$
can be computed from homological data of the infinite cyclic cover of the knot complement
$\operatorname {\mathrm {Bl}}(K)$
can be computed from homological data of the infinite cyclic cover of the knot complement
![]() $S^3\setminus K$
. To access information about K beyond the abelian covers of
$S^3\setminus K$
. To access information about K beyond the abelian covers of
![]() $S^3\setminus K$
, the idea of twisted invariants is to additionally keep track of a representation of the group
$S^3\setminus K$
, the idea of twisted invariants is to additionally keep track of a representation of the group
![]() $\pi _1(S^3 \setminus K).$
$\pi _1(S^3 \setminus K).$
In the case of polynomial invariants, the resulting theory of twisted Alexander polynomials, originally due to X. S. Lin [Reference Lin36] has been thoroughly developed, and we refer to [Reference Friedl and Vidussi24] for a survey of the vast literature on the subject. The present article aims to further develop the theory of twisted signatures and twisted Blanchfield forms. Before delving into the theory, we provide some motivation from knot concordance.
1.1 Knot concordance
A knot K is called slice if it bounds a locally flat embedded disc in
![]() $D^4$
[Reference Fox and Milnor17]. The first obstructions to sliceness date back to Fox and Milnor’s original paper on the subject and involve the Alexander polynomial
$D^4$
[Reference Fox and Milnor17]. The first obstructions to sliceness date back to Fox and Milnor’s original paper on the subject and involve the Alexander polynomial
![]() $\Delta _K$
. Later work of Levine [Reference Levine33] describes the algebraic concordance group, which, roughly speaking, encapsulates the obstructions to sliceness that come from the Seifert matrix, including
$\Delta _K$
. Later work of Levine [Reference Levine33] describes the algebraic concordance group, which, roughly speaking, encapsulates the obstructions to sliceness that come from the Seifert matrix, including
![]() $\Delta _K$
and the piecewise constant Levine-Tristram signature
$\Delta _K$
and the piecewise constant Levine-Tristram signature
Both
![]() $\Delta _K$
and
$\Delta _K$
and
![]() $\sigma _K$
(and, in fact, the entire algebraic concordance class of K) can be recovered from the so-called Blanchfield form, a non-singular, sesquilinear, Hermitian form on the Alexander module
$\sigma _K$
(and, in fact, the entire algebraic concordance class of K) can be recovered from the so-called Blanchfield form, a non-singular, sesquilinear, Hermitian form on the Alexander module
![]() $H_1(X_K;\mathbb {Z}[t^{\pm 1}])$
of K:
$H_1(X_K;\mathbb {Z}[t^{\pm 1}])$
of K:
A dozen years after Levine’s work, Casson and Gordon developed further signature invariants to obstruct certain algebraically slice knots from being slice [Reference Casson and Gordon6]. To a knot K and a prime power order character
![]() $\chi \colon H_1(\Sigma _n(K)) \to \mathbb {C}^\times $
(here,
$\chi \colon H_1(\Sigma _n(K)) \to \mathbb {C}^\times $
(here,
![]() $\Sigma _n(K)$
denotes the n-fold branched cover of K), their invariant takes the form of a Witt class
$\Sigma _n(K)$
denotes the n-fold branched cover of K), their invariant takes the form of a Witt class
Due to its 4-dimensional nature, this invariant is notoriously difficult to compute. In fact, for
![]() $\omega \in S^1$
, even the signatures
$\omega \in S^1$
, even the signatures
![]() $\operatorname {sign}_\omega ^{av}(\tau (K,\chi ))$
, obtained by taking the (averaged) signature at
$\operatorname {sign}_\omega ^{av}(\tau (K,\chi ))$
, obtained by taking the (averaged) signature at
![]() $t=\omega $
of a matrix representative of
$t=\omega $
of a matrix representative of
![]() $\tau (K,\chi )$
, remain difficult to approach in general. For instance, while
$\tau (K,\chi )$
, remain difficult to approach in general. For instance, while
![]() $\operatorname {sign}_1^{av}(\tau (K,\chi ))$
can be computed for genus one knots [Reference Gilmer26, Theorem 3.5], in general it can only be estimated in terms of simpler invariants; see, for example, [Reference Casson and Gordon6, Theorem 3] and [Reference Gilmer26, Theorem 3.4]. While applications of Casson-Gordon theory are numerous, our aim is to develop new methods to calculate
$\operatorname {sign}_1^{av}(\tau (K,\chi ))$
can be computed for genus one knots [Reference Gilmer26, Theorem 3.5], in general it can only be estimated in terms of simpler invariants; see, for example, [Reference Casson and Gordon6, Theorem 3] and [Reference Gilmer26, Theorem 3.4]. While applications of Casson-Gordon theory are numerous, our aim is to develop new methods to calculate
![]() $\operatorname {sign}_\omega ^{av}(\tau (K,\chi ))$
and, following [Reference Hedden, Kirk and Livingston27], to apply them to study the linear independence of algebraic knots in the knot concordance [Reference Conway, Kim and Politarczyk15].
$\operatorname {sign}_\omega ^{av}(\tau (K,\chi ))$
and, following [Reference Hedden, Kirk and Livingston27], to apply them to study the linear independence of algebraic knots in the knot concordance [Reference Conway, Kim and Politarczyk15].
Returning to the broader picture, additional information from the Witt class
![]() $\tau (K,\chi )$
was later made accessible by Kirk and Livingston by means of twisted Alexander polynomials [Reference Kirk and Livingston30]. As in the abelian setting, efforts to encompass both signature and polynomial obstructions then led Miller and Powell [Reference Miller and Powell40] to define a metabelian Blanchfield form
$\tau (K,\chi )$
was later made accessible by Kirk and Livingston by means of twisted Alexander polynomials [Reference Kirk and Livingston30]. As in the abelian setting, efforts to encompass both signature and polynomial obstructions then led Miller and Powell [Reference Miller and Powell40] to define a metabelian Blanchfield form
in order to efficiently detect knots in the quotient
![]() $\mathcal {F}_2/\mathcal {F}_{2.5}$
of the solvable filtration of [Reference Cochran, Orr and Teichner9]. Here,
$\mathcal {F}_2/\mathcal {F}_{2.5}$
of the solvable filtration of [Reference Cochran, Orr and Teichner9]. Here,
![]() $M_K$
denotes the
$M_K$
denotes the
![]() $3$
-manifold obtained by
$3$
-manifold obtained by
![]() $0$
-framed surgery on K.
$0$
-framed surgery on K.
Our goal is to use twisted Blanchfield pairings to define an algorithmically computable twisted signature function that generalizes both the Levine-Tristram signature
![]() $\sigma _K$
and the Casson-Gordon signatures
$\sigma _K$
and the Casson-Gordon signatures
![]() $\operatorname {sign}_\omega ^{av}(\tau (K,\chi ))$
; the algorithm is described in [Reference Borodzik, Conway and Politarczyk2, Subsection 1.4] and can be implemented in a computer for any knot K, as long as the complex roots of the twisted Alexander polynomial
$\operatorname {sign}_\omega ^{av}(\tau (K,\chi ))$
; the algorithm is described in [Reference Borodzik, Conway and Politarczyk2, Subsection 1.4] and can be implemented in a computer for any knot K, as long as the complex roots of the twisted Alexander polynomial
![]() $\Delta _K^{\alpha (K,\chi )}(t)$
that have modulus one can be determined exactly. The analogy we have in mind being that the Levine-Tristram signature
$\Delta _K^{\alpha (K,\chi )}(t)$
that have modulus one can be determined exactly. The analogy we have in mind being that the Levine-Tristram signature
![]() $\sigma _K$
can be recovered from the Blanchfield form
$\sigma _K$
can be recovered from the Blanchfield form
![]() $\operatorname {\mathrm {Bl}}(K)$
. This goal can be formulated more broadly in the context of twisted knot invariants.
$\operatorname {\mathrm {Bl}}(K)$
. This goal can be formulated more broadly in the context of twisted knot invariants.
1.2 The twisted signature function of a knot
We now recall the setup that goes into defining twisted invariants and discuss the properties of our twisted signature function. Given a field
![]() $\mathbb {F}$
and a space X, a representation
$\mathbb {F}$
and a space X, a representation
![]() $\alpha \colon \pi _1(X) \to GL_n({\mathbb {F}}[t^{\pm 1}])$
is called acyclic if the twisted homology groups
$\alpha \colon \pi _1(X) \to GL_n({\mathbb {F}}[t^{\pm 1}])$
is called acyclic if the twisted homology groups
![]() $H_k(X;{\mathbb {F}}[t^{\pm 1}]^n_\alpha )$
are
$H_k(X;{\mathbb {F}}[t^{\pm 1}]^n_\alpha )$
are
![]() ${\mathbb {F}}[t^{\pm 1}]$
-torsion for all k. Write
${\mathbb {F}}[t^{\pm 1}]$
-torsion for all k. Write
![]() $M_K$
for the 3-manifold obtained by 0-framed surgery on the knot K, and fix a unitary acyclic representation
$M_K$
for the 3-manifold obtained by 0-framed surgery on the knot K, and fix a unitary acyclic representation
![]() $\alpha \colon \pi _1(M_K) \to GL_n({\mathbb {F}}[t^{\pm 1}])$
. Here, a matrix
$\alpha \colon \pi _1(M_K) \to GL_n({\mathbb {F}}[t^{\pm 1}])$
. Here, a matrix
![]() $A \in GL_n({\mathbb {F}}[t^{\pm 1}])$
is called unitary if
$A \in GL_n({\mathbb {F}}[t^{\pm 1}])$
is called unitary if
![]() $A(A^\#)^T=\operatorname {id}$
, where
$A(A^\#)^T=\operatorname {id}$
, where
![]() $\#$
denotes the involution whose componentwise effect is
$\#$
denotes the involution whose componentwise effect is
![]() $\sum a_it^i \mapsto \sum \overline {a}_it^{-i}$
(we write
$\sum a_it^i \mapsto \sum \overline {a}_it^{-i}$
(we write
![]() $\overline {a}$
for the complex conjugate of
$\overline {a}$
for the complex conjugate of
![]() $a \in \mathbb {F}$
), and a representation
$a \in \mathbb {F}$
), and a representation
![]() $\alpha $
is unitary if
$\alpha $
is unitary if
![]() $\alpha (g)$
is a unitary matrix, for any
$\alpha (g)$
is a unitary matrix, for any
![]() $g \in \pi _{1}(M_{K})$
.
$g \in \pi _{1}(M_{K})$
.
Associated to this data, there is a twisted Alexander polynomial
![]() $\Delta ^\alpha _{K}(t)$
[Reference Lin36, Reference Wada44, Reference Kirk and Livingston30] and a twisted Blanchfield form
$\Delta ^\alpha _{K}(t)$
[Reference Lin36, Reference Wada44, Reference Kirk and Livingston30] and a twisted Blanchfield form
![]() $\operatorname {\mathrm {Bl}}_\alpha (K)$
[Reference Powell42, Reference Miller and Powell40]. When
$\operatorname {\mathrm {Bl}}_\alpha (K)$
[Reference Powell42, Reference Miller and Powell40]. When
![]() $\alpha $
is induced by the abelianization
$\alpha $
is induced by the abelianization
![]() $ab$
, these invariants respectively coincide with the classical Alexander polynomial
$ab$
, these invariants respectively coincide with the classical Alexander polynomial
![]() $\Delta _K(t)$
and Blanchfield form
$\Delta _K(t)$
and Blanchfield form
![]() $\operatorname {\mathrm {Bl}}(K)$
, while metabelian invariants, such as the Casson-Gordon invariants, are recovered by considering a representation
$\operatorname {\mathrm {Bl}}(K)$
, while metabelian invariants, such as the Casson-Gordon invariants, are recovered by considering a representation
whose precise definition will be recalled in Subsection 4.1.
This paper develops a corresponding theory of twisted signature functions and further studies twisted Blanchfield forms. The following theorem, which combines the results of Proposition 3.4, Remark 3.3, Proposition 3.9 and Corollary 3.16, summarizes some of the properties of our twisted signatures.
Theorem 1.1. Suppose
![]() $\mathbb {F}$
is either
$\mathbb {F}$
is either
![]() $\mathbb {R}$
or
$\mathbb {R}$
or
![]() $\mathbb {C}$
. Given a knot K and a unitary acyclic representation
$\mathbb {C}$
. Given a knot K and a unitary acyclic representation
![]() $\alpha \colon \pi _1(M_K) \to GL_d({\mathbb {F}}[t^{\pm 1}])$
, there is a function
$\alpha \colon \pi _1(M_K) \to GL_d({\mathbb {F}}[t^{\pm 1}])$
, there is a function
![]() $\sigma _{K,\alpha }\colon S^1 \to \mathbb {Z}$
with the following properties:
$\sigma _{K,\alpha }\colon S^1 \to \mathbb {Z}$
with the following properties:
-
(1) Piecewise continuity. The twisted signature function
 $\sigma _{K,\alpha }$
is locally constant on the complement of the zeroes of the twisted Alexander polynomial
$\sigma _{K,\alpha }$
is locally constant on the complement of the zeroes of the twisted Alexander polynomial
 $\Delta _K^\alpha (t)$
.
$\Delta _K^\alpha (t)$
. -
(2) Obstruction to sliceness. The averaged signature function
(1.2)provides an obstruction to sliceness: if K is sliced by a disc $$ \begin{align} \sigma^{av}_{(K,\alpha)}(\omega)=\frac12\left(\lim_{\theta\to 0^+}\sigma_{(K,\alpha)}(e^{i\theta}\omega)+\lim_{\theta\to 0^-}\sigma_{(K,\alpha)}(e^{i\theta}\omega)\right) \end{align} $$
$$ \begin{align} \sigma^{av}_{(K,\alpha)}(\omega)=\frac12\left(\lim_{\theta\to 0^+}\sigma_{(K,\alpha)}(e^{i\theta}\omega)+\lim_{\theta\to 0^-}\sigma_{(K,\alpha)}(e^{i\theta}\omega)\right) \end{align} $$
 $D \subset D^4$
and if
$D \subset D^4$
and if
 $\alpha $
extends to a unitary acyclic representation
$\alpha $
extends to a unitary acyclic representation
 $\pi _1(D^4 \setminus \mathcal {N}(D)) \to GL_d({\mathbb {F}}[t^{\pm 1}])$
, then
$\pi _1(D^4 \setminus \mathcal {N}(D)) \to GL_d({\mathbb {F}}[t^{\pm 1}])$
, then
 $\sigma _{K,\alpha }^{av} \equiv 0$
.
$\sigma _{K,\alpha }^{av} \equiv 0$
.
-
(3) Behavior under satellite operations. Let
 $P,J$
be knots and let
$P,J$
be knots and let
 $\eta \subset S^3\setminus P \subset M_P$
be a simple closed curve. Assume that
$\eta \subset S^3\setminus P \subset M_P$
be a simple closed curve. Assume that
 $\gamma \colon \pi _1(M_{P(J,\eta )}) \to GL_d({\mathbb {F}}[t^{\pm 1}])$
is a unitary acyclic representation such that
$\gamma \colon \pi _1(M_{P(J,\eta )}) \to GL_d({\mathbb {F}}[t^{\pm 1}])$
is a unitary acyclic representation such that
 $\det (\operatorname {id} -\gamma (\eta )) \neq 0$
and
$\det (\operatorname {id} -\gamma (\eta )) \neq 0$
and
 $\gamma (\mu _\eta )=\operatorname {id}$
, where
$\gamma (\mu _\eta )=\operatorname {id}$
, where
 $\mu _\eta $
denotes the meridian of
$\mu _\eta $
denotes the meridian of
 $\eta $
. Then, for every
$\eta $
. Then, for every
 $\omega \in S^1$
, the averaged twisted signature satisfies
$\omega \in S^1$
, the averaged twisted signature satisfies  $$ \begin{align*}\sigma^{av}_{P(K,\eta),\gamma}(\omega)= \sigma^{av}_{P,\gamma_P}(\omega)+\sigma^{av}_{K,\gamma_K}(\omega).\end{align*} $$
$$ \begin{align*}\sigma^{av}_{P(K,\eta),\gamma}(\omega)= \sigma^{av}_{P,\gamma_P}(\omega)+\sigma^{av}_{K,\gamma_K}(\omega).\end{align*} $$
-
(4) Relationship with the Levine-Tristram signature: if the representation
 $\alpha $
is induced by the abelianization, then
$\alpha $
is induced by the abelianization, then
 $\sigma _{K,\alpha }(\omega )$
coincides with
$\sigma _{K,\alpha }(\omega )$
coincides with
 $\sigma _K(\omega )$
for all
$\sigma _K(\omega )$
for all
 $\omega \in S^1$
.
$\omega \in S^1$
.
Theorem 1.1 shows that the twisted signature function is related to the twisted Alexander polynomial in the same way as the Levine-Tristram signature is related to the Alexander polynomial. We refer to Proposition 3.4 for some elementary properties of the twisted signature function but now describe how the Casson-Gordon signatures can be recovered from our signature function.
Theorem 1.2. Fix a prime power order character
![]() $\chi \colon H_1(\Sigma _n(K)) \to \mathbb {Z}_m$
and
$\chi \colon H_1(\Sigma _n(K)) \to \mathbb {Z}_m$
and
![]() $\omega \in S^1$
. When
$\omega \in S^1$
. When
![]() $\alpha =\alpha (n,\chi )$
is the metabelian representation mentioned in (1.1), the averaged twisted signature function is related to the Casson-Gordon signature
$\alpha =\alpha (n,\chi )$
is the metabelian representation mentioned in (1.1), the averaged twisted signature function is related to the Casson-Gordon signature
![]() $\operatorname {sign}_\omega ^{av}(\tau (K,\chi ))$
in the following way:
$\operatorname {sign}_\omega ^{av}(\tau (K,\chi ))$
in the following way:
Theorem 1.2 leads to what appears to be the first algorithm to explicitly compute the difference
![]() $-\operatorname {sign}_\omega ^{av}(\tau (K,\chi ))+\operatorname {sign}_1^{av}(\tau (K,\chi ))$
of Casson-Gordon signatures from a knot diagram; the algorithm is described and implemented in [Reference Borodzik, Conway and Politarczyk2]. In particular, while both
$-\operatorname {sign}_\omega ^{av}(\tau (K,\chi ))+\operatorname {sign}_1^{av}(\tau (K,\chi ))$
of Casson-Gordon signatures from a knot diagram; the algorithm is described and implemented in [Reference Borodzik, Conway and Politarczyk2]. In particular, while both
![]() $\operatorname {sign}_\omega ^{av}(\tau (K,\chi ))$
and
$\operatorname {sign}_\omega ^{av}(\tau (K,\chi ))$
and
![]() $\operatorname {sign}_1^{av}(\tau (K,\chi ))$
are rational numbers (as we recall in Definition 4.12), Theorem 1.2 implies that their difference is in fact an integer.
$\operatorname {sign}_1^{av}(\tau (K,\chi ))$
are rational numbers (as we recall in Definition 4.12), Theorem 1.2 implies that their difference is in fact an integer.
Summarizing, the twisted signature function
![]() $\sigma _K \colon S^1 \to \mathbb {Z}$
satisfies properties analogous to the Levine-Tristram signature
$\sigma _K \colon S^1 \to \mathbb {Z}$
satisfies properties analogous to the Levine-Tristram signature
![]() $\sigma _K$
, recovers it when
$\sigma _K$
, recovers it when
![]() $\alpha $
is induced by the abelianization, and is related to Casson-Gordon signatures for
$\alpha $
is induced by the abelianization, and is related to Casson-Gordon signatures for
![]() $\alpha =\alpha (K,\chi )$
.
$\alpha =\alpha (K,\chi )$
.
Remark 1.3. In the abelian setting, the Levine-Tristram signature
![]() $\sigma _K(\omega )$
of a knot K at
$\sigma _K(\omega )$
of a knot K at
![]() $\omega \in S^1$
is defined as
$\omega \in S^1$
is defined as
where V is any Seifert matrix for K. In the twisted setting, the lack of a Seifert matrix means that there is no straightforward way of defining a twisted analogue of
![]() $\sigma _K$
by 3-dimensional means.
$\sigma _K$
by 3-dimensional means.
However, while
![]() $4$
-dimensional approaches based on the eta invariant [Reference Atiyah, Patodi and Singer1] have been studied [Reference Levine35, Reference Friedl19], the resulting signature invariants are unwieldly and, as far as we can tell, their relation to other twisted invariants is less apparent.
$4$
-dimensional approaches based on the eta invariant [Reference Atiyah, Patodi and Singer1] have been studied [Reference Levine35, Reference Friedl19], the resulting signature invariants are unwieldly and, as far as we can tell, their relation to other twisted invariants is less apparent.
As the signatures of Theorem 1.1 are defined using twisted Blanchfield forms, we briefly review the setup underlying these linking forms and our results concerning them.
1.3 The twisted Blanchfield forms
Given a closed, connected, oriented 3-manifold N and a unitary acyclic representation
![]() $\alpha \colon \pi _1(N) \to GL_n({\mathbb {F}}[t^{\pm 1}])$
, the twisted Blanchfield form is a Hermitian, non-singular sesqulinear form
$\alpha \colon \pi _1(N) \to GL_n({\mathbb {F}}[t^{\pm 1}])$
, the twisted Blanchfield form is a Hermitian, non-singular sesqulinear form
While this pairing was first studied systematically by Powell [Reference Powell42] and, for
![]() $\alpha =\alpha (n,\chi )$
, by Miller and Powell [Reference Miller and Powell40], its roots are to be found in the earlier work of Cochran-Orr-Teichner [Reference Cochran, Orr and Teichner9] in the non-commutative setting.
$\alpha =\alpha (n,\chi )$
, by Miller and Powell [Reference Miller and Powell40], its roots are to be found in the earlier work of Cochran-Orr-Teichner [Reference Cochran, Orr and Teichner9] in the non-commutative setting.
The work of Powell laid the technical groundwork to the study of
![]() $\operatorname {\mathrm {Bl}}_\alpha (N)$
and proved that the pairing is Hermitian and non-singular. On the whole however, few general properties of
$\operatorname {\mathrm {Bl}}_\alpha (N)$
and proved that the pairing is Hermitian and non-singular. On the whole however, few general properties of
![]() $\operatorname {\mathrm {Bl}}_\alpha (N)$
have been established so far. A second aim of this paper is to prove further properties of
$\operatorname {\mathrm {Bl}}_\alpha (N)$
have been established so far. A second aim of this paper is to prove further properties of
![]() $\operatorname {\mathrm {Bl}}_\alpha (N)$
, when
$\operatorname {\mathrm {Bl}}_\alpha (N)$
, when
![]() $N=M_K$
is the
$N=M_K$
is the
![]() $0$
-framed surgery along K, in which case we write
$0$
-framed surgery along K, in which case we write
When
![]() $\alpha $
is induced by abelianization,
$\alpha $
is induced by abelianization,
![]() $\operatorname {\mathrm {Bl}}_\alpha (K)=\operatorname {\mathrm {Bl}}(K)$
is the ‘classical’ Blanchfield pairing of K.
$\operatorname {\mathrm {Bl}}_\alpha (K)=\operatorname {\mathrm {Bl}}(K)$
is the ‘classical’ Blanchfield pairing of K.
Our first result about twisted Blanchfield forms (which is similar to the work of Miller and Powell in the metabelian setting) describes how
![]() $\operatorname {\mathrm {Bl}}_\alpha (K)$
leads to sliceness obstructions.
$\operatorname {\mathrm {Bl}}_\alpha (K)$
leads to sliceness obstructions.
Proposition 1.4 (see Proposition 3.9)
Let K be a slice knot and let
![]() $\beta \colon \pi _{1}(M_K) \to GL_d(\mathbb {F}[t^{\pm 1}])$
be a unitary acyclic representation. If
$\beta \colon \pi _{1}(M_K) \to GL_d(\mathbb {F}[t^{\pm 1}])$
be a unitary acyclic representation. If
![]() $D\subset D^4 $
is a slice disk for K and there is a unitary acyclic representation
$D\subset D^4 $
is a slice disk for K and there is a unitary acyclic representation
![]() $\gamma \colon \pi _{1}(D^4 \setminus \mathcal {N}(D)) \to GL_d(\mathbb {F}[t^{\pm 1}])$
extending
$\gamma \colon \pi _{1}(D^4 \setminus \mathcal {N}(D)) \to GL_d(\mathbb {F}[t^{\pm 1}])$
extending
![]() $\beta $
, then the twisted Blanchfield pairing
$\beta $
, then the twisted Blanchfield pairing
![]() $\operatorname {\mathrm {Bl}}_{\beta }(K)$
is metabolic.Footnote 1
$\operatorname {\mathrm {Bl}}_{\beta }(K)$
is metabolic.Footnote 1
One result we wish to emphasize concerns the behaviour of the twisted Blanchfield form under satellite operations. For the classical Blanchfield form, a satellite formula was proved by Livingston-Melvin [Reference Livingston and Melvin39]: given a winding number n satellite operator
![]() $P \subset S^1 \times D^2$
, this formula reads as
$P \subset S^1 \times D^2$
, this formula reads as
and can be seen as a generalization of the satellite formula for the Levine-Tristram signature [Reference Litherland37, Reference Shinohara43]. In the metabelian case, a satellite formula for the Casson-Gordon invariants was proved by Litherland [Reference Litherland38], while satellite formulas for higher order signatures can be found in [Reference Cochran, Orr and Teichner10]. Building on the algebraic machinery from [Reference Borodzik, Conway and Politarczyk3] and on work of Friedl-Leidy-Nagel-Powell [Reference Friedl, Leidy, Nagel and Powell21], Theorem 3.11 provides a satellite formula for twisted Blanchfield forms. A particular case of this theorem reads as follows.
Theorem 1.5. Let
![]() $J,P$
be knots and let
$J,P$
be knots and let
![]() $\eta \subset S^3\setminus P \subset M_P$
be a simple closed curve. Assume that
$\eta \subset S^3\setminus P \subset M_P$
be a simple closed curve. Assume that
![]() $\gamma \colon \pi _1(M_{P(J,\eta )}) \to GL_d({\mathbb {F}}[t^{\pm 1}])$
is a unitary acyclic representation such that
$\gamma \colon \pi _1(M_{P(J,\eta )}) \to GL_d({\mathbb {F}}[t^{\pm 1}])$
is a unitary acyclic representation such that
![]() $\det (\operatorname {id} -\gamma (\eta )) \neq ~0$
and
$\det (\operatorname {id} -\gamma (\eta )) \neq ~0$
and
![]() $\gamma (\mu _\eta )=\operatorname {id}$
, where
$\gamma (\mu _\eta )=\operatorname {id}$
, where
![]() $\mu _\eta $
denotes the meridian of
$\mu _\eta $
denotes the meridian of
![]() $\eta $
. Then the twisted Blanchfield form
$\eta $
. Then the twisted Blanchfield form
![]() $Bl_\gamma (P(J,\eta ))$
is Witt equivalent to
$Bl_\gamma (P(J,\eta ))$
is Witt equivalent to
![]() $\operatorname {\mathrm {Bl}}_{\gamma _P}(P) \oplus \operatorname {\mathrm {Bl}}_{\gamma _J}(J).$
$\operatorname {\mathrm {Bl}}_{\gamma _P}(P) \oplus \operatorname {\mathrm {Bl}}_{\gamma _J}(J).$
Here, two linking forms
![]() $(M_1,\lambda _1)$
and
$(M_1,\lambda _1)$
and
![]() $(M_2,\lambda _2)$
are Witt equivalent if
$(M_2,\lambda _2)$
are Witt equivalent if
![]() $(M_{1} \oplus M_{2}, \lambda _{1} \oplus -\lambda _{2})$
is metabolic. In particular, Theorem 1.5 implies the third item of Theorem 1.1 because, as we recall in Proposition 1.6 below, Witt equivalent linking forms have identical averaged signature functions.
$(M_{1} \oplus M_{2}, \lambda _{1} \oplus -\lambda _{2})$
is metabolic. In particular, Theorem 1.5 implies the third item of Theorem 1.1 because, as we recall in Proposition 1.6 below, Witt equivalent linking forms have identical averaged signature functions.
In Theorem 4.19, we prove a satellite formula for the metabelian Blanchfield form
![]() $\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(K)$
; the proof uses Theorem 1.5 and some representation theory. This result then underpines further work of the second and third author with Min Hoon Kim concerning applications of our theory to the study of linear independence of algebraic knots in knot concordance [Reference Conway, Kim and Politarczyk15].
$\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(K)$
; the proof uses Theorem 1.5 and some representation theory. This result then underpines further work of the second and third author with Min Hoon Kim concerning applications of our theory to the study of linear independence of algebraic knots in knot concordance [Reference Conway, Kim and Politarczyk15].
1.4 Linking forms and their signature functions
In order to outline the construction of the twisted signature
![]() $\sigma _{K,\alpha }$
, we recall some properties of the signature function of a linking form from [Reference Borodzik, Conway and Politarczyk3]. First, recall that given a PID R with involution
$\sigma _{K,\alpha }$
, we recall some properties of the signature function of a linking form from [Reference Borodzik, Conway and Politarczyk3]. First, recall that given a PID R with involution
![]() $x \mapsto x^\#$
and field of fractions Q, a linking form refers to a sesquilinear, Hermitian form
$x \mapsto x^\#$
and field of fractions Q, a linking form refers to a sesquilinear, Hermitian form
on a torsion R-module M. Such a linking form is metabolic if there exists a submodule
![]() $P \subset M$
with
$P \subset M$
with
![]() $P=P^\perp $
, while
$P=P^\perp $
, while
![]() $(M,\lambda )$
is represented by an
$(M,\lambda )$
is represented by an
![]() $(n\times n)$
-non-degenerate Hermitian matrix
$(n\times n)$
-non-degenerate Hermitian matrix
![]() $A(t)$
if it is isometric to the linking form
$A(t)$
if it is isometric to the linking form
 $$ \begin{align*} \lambda_{A(t)} \colon {\mathbb{F}}[t^{\pm 1}]^n/A(t) \times {\mathbb{F}}[t^{\pm 1}]^n/A(t) &\to \mathbb{F}(t)/{\mathbb{F}}[t^{\pm 1}] \\ (x,y) &\mapsto x^TA(t)^{-1}y^\#. \end{align*} $$
$$ \begin{align*} \lambda_{A(t)} \colon {\mathbb{F}}[t^{\pm 1}]^n/A(t) \times {\mathbb{F}}[t^{\pm 1}]^n/A(t) &\to \mathbb{F}(t)/{\mathbb{F}}[t^{\pm 1}] \\ (x,y) &\mapsto x^TA(t)^{-1}y^\#. \end{align*} $$
The next proposition summarizes several properties of the signature functions built in [Reference Borodzik, Conway and Politarczyk3].
Proposition 1.6. Given a non-singular linking form
![]() $(M,\lambda )$
over
$(M,\lambda )$
over
![]() ${\mathbb {F}}[t^{\pm 1}]$
, where
${\mathbb {F}}[t^{\pm 1}]$
, where
![]() $\mathbb {F} = \mathbb {R}$
or
$\mathbb {F} = \mathbb {R}$
or
![]() $\mathbb {C}$
, there exists a signature function
$\mathbb {C}$
, there exists a signature function
![]() $\sigma _{(M,\lambda )} \colon S^1 \to \mathbb {Z}$
that satisfies the following properties:
$\sigma _{(M,\lambda )} \colon S^1 \to \mathbb {Z}$
that satisfies the following properties:
-
(S-1) The signature function is locally constant on
 $S^1 \setminus \lbrace \xi \in S^1 \ | \ \Delta _M(\xi )=0 \rbrace $
, where
$S^1 \setminus \lbrace \xi \in S^1 \ | \ \Delta _M(\xi )=0 \rbrace $
, where
 $\Delta _M$
denotes the order of the
$\Delta _M$
denotes the order of the
 ${\mathbb {F}}[t^{\pm 1}]$
-module M.
${\mathbb {F}}[t^{\pm 1}]$
-module M. -
(S-2) If
 $\mathbb {F} = \mathbb {R}$
, then we have
$\mathbb {F} = \mathbb {R}$
, then we have  $$ \begin{align*}\sigma_{(M,\lambda)}(\overline{\xi})=\sigma_{(M,\lambda)}(\xi).\end{align*} $$
$$ \begin{align*}\sigma_{(M,\lambda)}(\overline{\xi})=\sigma_{(M,\lambda)}(\xi).\end{align*} $$
-
(S-3) The signature function is additive:
 $$ \begin{align*}\sigma_{(M_1,\lambda_1) \oplus (M_2,\lambda_2)}(\xi)=\sigma_{(M_1,\lambda_1)}(\xi)+\sigma_{(M_2,\lambda_2)}(\xi).\end{align*} $$
$$ \begin{align*}\sigma_{(M_1,\lambda_1) \oplus (M_2,\lambda_2)}(\xi)=\sigma_{(M_1,\lambda_1)}(\xi)+\sigma_{(M_2,\lambda_2)}(\xi).\end{align*} $$
-
(S-4) The averaged signature function
is locally constant and additive, and vanishes if $$ \begin{align*}\sigma^{av}_{(M,\lambda)}(\xi)=\frac12\left(\lim_{\theta\to 0^+}\sigma_{(M,\lambda)}(e^{i\theta}\xi)+\lim_{\theta\to 0^-}\sigma_{(M,\lambda)}(e^{i\theta}\xi)\right) \end{align*} $$
$$ \begin{align*}\sigma^{av}_{(M,\lambda)}(\xi)=\frac12\left(\lim_{\theta\to 0^+}\sigma_{(M,\lambda)}(e^{i\theta}\xi)+\lim_{\theta\to 0^-}\sigma_{(M,\lambda)}(e^{i\theta}\xi)\right) \end{align*} $$
 $(M,\lambda )$
is metabolic.
$(M,\lambda )$
is metabolic.
-
(S-5) If
 $(M,\lambda )$
is represented by a matrix
$(M,\lambda )$
is represented by a matrix
 $A(t)$
, then the averaged signature function satisfies
$A(t)$
, then the averaged signature function satisfies  $$ \begin{align*}\sigma^{av}_{(M,\lambda)}(\xi) =\operatorname{sign}^{av} A(\xi)-\operatorname{sign}^{av}A(1).\end{align*} $$
$$ \begin{align*}\sigma^{av}_{(M,\lambda)}(\xi) =\operatorname{sign}^{av} A(\xi)-\operatorname{sign}^{av}A(1).\end{align*} $$
-
(S-6) A linking form
 $(M,\lambda )$
over
$(M,\lambda )$
over
 ${\mathbb {C}}[t^{\pm 1}]$
is representable if and only if
${\mathbb {C}}[t^{\pm 1}]$
is representable if and only if
 $\sigma ^{av}_{(M,\lambda )}(1)=0$
.
$\sigma ^{av}_{(M,\lambda )}(1)=0$
.
Proof. The five first properties are in listed in [Reference Borodzik, Conway and Politarczyk3, Subsection 1.5]. Item (S-6) is proved in [Reference Borodzik, Conway and Politarczyk3, Proposition 5.7 and Corollary 5.15].
The twisted signature function of Theorem 1.1 is defined as the signature function of the non-singular linking form
![]() $(H_1(M_K;{\mathbb {F}}[t^{\pm 1}]_\alpha ^n),\operatorname {\mathrm {Bl}}_\alpha (K))$
. As a consequence, properties of the twisted signature (such as those listed in Theorem 1.1) are established by studying the behavior of the twisted Blanchfield form and then applying Proposition 1.6.
$(H_1(M_K;{\mathbb {F}}[t^{\pm 1}]_\alpha ^n),\operatorname {\mathrm {Bl}}_\alpha (K))$
. As a consequence, properties of the twisted signature (such as those listed in Theorem 1.1) are established by studying the behavior of the twisted Blanchfield form and then applying Proposition 1.6.
Organization
In Section 2, we recall some background on twisted homology and twisted Blanchfield forms; we also relate twisted Blanchfield forms to their non-commutative analogues. In Section 3, we define our twisted signature invariants and prove several of the properties stated in Theorem 1.1; additionally in Theorem 3.11, we prove our satellite formula for the twisted Blanchfield form. In Section 4, we focus on metabelian representations, relate our invariants to Casson-Gordon signatures (Theorem 4.14) and prove the satellite formulas for the metabelian Blanchfield form (Theorem 4.19). The Appendix contains further details on twisted homology as well as the proof of Corollary 4.6.
Conventions
If R is a commutative ring and
![]() $f,g\in R$
, we write
$f,g\in R$
, we write
![]() $f\doteq g$
if there exists a unit
$f\doteq g$
if there exists a unit
![]() $u\in R$
such that
$u\in R$
such that
![]() $f=ug$
. For a ring R with involution, we denote this involution by
$f=ug$
. For a ring R with involution, we denote this involution by
![]() $x\mapsto x^\#$
; the symbol
$x\mapsto x^\#$
; the symbol
![]() $\overline {x}$
is reserved for the complex conjugation. In particular, for
$\overline {x}$
is reserved for the complex conjugation. In particular, for
![]() $R={\mathbb {C}}[t^{\pm 1}]$
, the involution
$R={\mathbb {C}}[t^{\pm 1}]$
, the involution
![]() $(-)^\#$
is the composition of the complex conjugation with the map
$(-)^\#$
is the composition of the complex conjugation with the map
![]() $t\mapsto t^{-1}$
. Given an R-module M, we denote by
$t\mapsto t^{-1}$
. Given an R-module M, we denote by
![]() $M^\#$
the R-module that has the same underlying additive group as M, but for which the action by R on M is precomposed with the involution on R. For a matrix A over R, we write
$M^\#$
the R-module that has the same underlying additive group as M, but for which the action by R on M is precomposed with the involution on R. For a matrix A over R, we write
![]() ${A}^{\#T}$
for the transpose followed by the involution.
${A}^{\#T}$
for the transpose followed by the involution.
We work in the topological category unless otherwise stated. All manifolds are assumed to be compact, connected, based and oriented; if a manifold has a nonempty boundary, then the basepoint is assumed to be in the boundary. Maps between based spaces are understood to be basepoint preserving.
2 Twisted homology and twisted Blanchfield pairings
This section is organized as follows: in Subection 2.1, we review twisted (co)homology, in Subsection 2.2, we discuss twisted Blanchfield forms, and in Subsection 2.3, we relate twisted Blanchfield forms to their non-commutative counterparts.
2.1 Twisted homology and cohomology
In this subsection, we briefly review twisted (co)homology and twisted intersection forms. While standard references include [Reference Kirk and Livingston30, Reference Friedl and Kim20], we also refer the reader to [Reference Cha, Miller and Powell7, Section 3] for a thorough discussion of the twisted homology of disconnected manifolds and the resulting long exact sequence of pairs. Additionally, for ease of exposition, we will focus on CW complexes. This is not cause a cause for concern, when working with 3-manifolds and smooth 4-manifolds, both of which admit the structure of finite CW complexes of the appropriate dimension; we refer to [Reference Friedl, Nagel, Orson and Powell25, Section 4] for the precise statements and references. However, while (topological)
![]() $4$
-manifolds need not admit CW structures, arguments involving twisted homology and Poincaré duality can nevertheless be carried out as in the smooth category (using singular chain complexes instead of cellular chain complexes): this is nontrivial, and we refer the interested reader to (Reference Friedl, Nagel, Orson and Powell25, Appendix A) for many more details and references.Footnote 2
$4$
-manifolds need not admit CW structures, arguments involving twisted homology and Poincaré duality can nevertheless be carried out as in the smooth category (using singular chain complexes instead of cellular chain complexes): this is nontrivial, and we refer the interested reader to (Reference Friedl, Nagel, Orson and Powell25, Appendix A) for many more details and references.Footnote 2
Let X be a path connected CW complex and let
![]() $Y \subset X$
be a possibly empty subcomplex. Use
$Y \subset X$
be a possibly empty subcomplex. Use
![]() $p \colon \widetilde {X} \to X$
to denote the universal cover of X and set
$p \colon \widetilde {X} \to X$
to denote the universal cover of X and set
![]() $\widetilde {Y}:=p^{-1}(Y)$
. The left action of
$\widetilde {Y}:=p^{-1}(Y)$
. The left action of
![]() $\pi _1(X)$
on
$\pi _1(X)$
on
![]() $\widetilde {X}$
endows the chain complex
$\widetilde {X}$
endows the chain complex
![]() $C_*(\widetilde {X},\widetilde {Y})$
with the structure of a left
$C_*(\widetilde {X},\widetilde {Y})$
with the structure of a left
![]() $\mathbb {Z}[\pi _1(X)]$
-module. Moreover, let R be a ring and let M be a
$\mathbb {Z}[\pi _1(X)]$
-module. Moreover, let R be a ring and let M be a
![]() $(R,\mathbb {Z}[\pi _1(X)])$
-module. The chain complexes
$(R,\mathbb {Z}[\pi _1(X)])$
-module. The chain complexes
 $$ \begin{align*} & C_*(X,Y;M):=M \otimes_{\mathbb{Z}[\pi_1(X)]}C_*(\widetilde{X},\widetilde{Y}) \\ & C^*(X,Y;M):=\operatorname{Hom}_{\text{right-}\mathbb{Z}[\pi_1(X)]}(C_*(\widetilde{X}, \widetilde{Y} )^\#,M) \end{align*} $$
$$ \begin{align*} & C_*(X,Y;M):=M \otimes_{\mathbb{Z}[\pi_1(X)]}C_*(\widetilde{X},\widetilde{Y}) \\ & C^*(X,Y;M):=\operatorname{Hom}_{\text{right-}\mathbb{Z}[\pi_1(X)]}(C_*(\widetilde{X}, \widetilde{Y} )^\#,M) \end{align*} $$
of left R-modules will be called the twisted (co)chain complex of
![]() $(X,Y)$
with coefficients in M. The corresponding homology left R-modules
$(X,Y)$
with coefficients in M. The corresponding homology left R-modules
![]() $H_*(X,Y;M)$
and
$H_*(X,Y;M)$
and
![]() $H^*(X,Y;M)$
will be called the twisted (co)homology modules of
$H^*(X,Y;M)$
will be called the twisted (co)homology modules of
![]() $(X,Y)$
with coefficients in M.
$(X,Y)$
with coefficients in M.
Assume that R is endowed with an involution
![]() $x \mapsto x^\#$
. Let
$x \mapsto x^\#$
. Let
![]() $M,M'$
be
$M,M'$
be
![]() $(R,\mathbb {Z}[\pi _1(X)])$
-bimodules and let S be a
$(R,\mathbb {Z}[\pi _1(X)])$
-bimodules and let S be a
![]() $(R,R)$
-bimodule. Furthermore, let
$(R,R)$
-bimodule. Furthermore, let
![]() $\langle -,-\rangle \colon M' \times M \to S$
be a non-singular
$\langle -,-\rangle \colon M' \times M \to S$
be a non-singular
![]() $\pi _1(X)$
-invariant sesquilinear pairing, in the sense that
$\pi _1(X)$
-invariant sesquilinear pairing, in the sense that
![]() $\langle m\gamma , n\gamma \rangle =\langle m,n\rangle $
and
$\langle m\gamma , n\gamma \rangle =\langle m,n\rangle $
and
![]() $\langle rm,sn \rangle =r \langle m,n \rangle s^\#$
for all
$\langle rm,sn \rangle =r \langle m,n \rangle s^\#$
for all
![]() $\gamma \in \pi _1(X)$
, all
$\gamma \in \pi _1(X)$
, all
![]() $r,s \in R$
and all
$r,s \in R$
and all
![]() $m\in M, n \in M'$
. Non-singularity means that the induced map
$m\in M, n \in M'$
. Non-singularity means that the induced map
![]() $M\to \operatorname {\mathrm {Hom}}_{\text {left-}R}(M',S)^\#$
is an isomorphism. In this setting, as recalled in the appendix (specifically Construction A.3), there is an evaluation map
$M\to \operatorname {\mathrm {Hom}}_{\text {left-}R}(M',S)^\#$
is an isomorphism. In this setting, as recalled in the appendix (specifically Construction A.3), there is an evaluation map
The evaluation map need not be an isomorphism. If R is a principal ideal domain, then the universal coefficient theorem implies that the cohomology group
![]() $H^i(X,Y;M)$
decomposes as the direct sum of
$H^i(X,Y;M)$
decomposes as the direct sum of
![]() $\operatorname {Hom}_{\text {left-}R}(H_i(X,Y;M'),S)^\#$
and
$\operatorname {Hom}_{\text {left-}R}(H_i(X,Y;M'),S)^\#$
and
![]() $\operatorname {Ext}^1_{\text {left-}R}(H_i(X,Y;M'),S)^\#$
. In general, the evaluation map can be studied using the universal coefficient spectral sequence [Reference Levine34, Theorem 2.3]. Returning to
$\operatorname {Ext}^1_{\text {left-}R}(H_i(X,Y;M'),S)^\#$
. In general, the evaluation map can be studied using the universal coefficient spectral sequence [Reference Levine34, Theorem 2.3]. Returning to
![]() $\pi _1(X)$
-invariant pairings, we now discuss two examples which we shall use throughout this section.
$\pi _1(X)$
-invariant pairings, we now discuss two examples which we shall use throughout this section.
Example 2.1. Let R be an integral domain with field of fractions Q. Given a positive integer d, let
![]() $\beta \colon \pi _1(X) \to GL_d(R)$
be a representation and use
$\beta \colon \pi _1(X) \to GL_d(R)$
be a representation and use
![]() $R^d_\beta $
to denote the
$R^d_\beta $
to denote the
![]() $(R,\mathbb {Z}[\pi _1(X)])$
-module whose right
$(R,\mathbb {Z}[\pi _1(X)])$
-module whose right
![]() $\mathbb {Z}[\pi _1(X)]$
-module structure is given by right multiplication by
$\mathbb {Z}[\pi _1(X)]$
-module structure is given by right multiplication by
![]() $\beta (\gamma )$
on row vectors for
$\beta (\gamma )$
on row vectors for
![]() $\gamma \in \pi _1(X)$
. Use
$\gamma \in \pi _1(X)$
. Use ![]() to denote the representation defined by
to denote the representation defined by ![]() and consider the pairings
and consider the pairings

Note that the use of the representation ![]() guarantees that these pairings are indeed
guarantees that these pairings are indeed
![]() $\pi _1(X)$
-invariant. In particular, if
$\pi _1(X)$
-invariant. In particular, if
![]() $\beta $
is a unitary representation (so that
$\beta $
is a unitary representation (so that ![]() ), then the two pairings displayed above give rise to evaluation maps
), then the two pairings displayed above give rise to evaluation maps
![]() $H^i(X,Y;Q/R \otimes _R R_\beta ^d) \to \operatorname {Hom}_{\text {left-}R}(H_i(X,Y;R_{\beta }^d),Q/R)^\#$
and
$H^i(X,Y;Q/R \otimes _R R_\beta ^d) \to \operatorname {Hom}_{\text {left-}R}(H_i(X,Y;R_{\beta }^d),Q/R)^\#$
and
![]() $H^i(X,Y; R_\beta ^d) \to \operatorname {Hom}_{\text {left-}R}(H_i(X,Y; R_{\beta }^d),R)^\#$
.
$H^i(X,Y; R_\beta ^d) \to \operatorname {Hom}_{\text {left-}R}(H_i(X,Y; R_{\beta }^d),R)^\#$
.
Next, we briefly review the definition of twisted intersection forms. Let W be a compact oriented n-manifold and let M be a
![]() $(R,\mathbb {Z}[\pi _1(W)])$
-bimodule. As we mentioned above, if W does not admit a CW structure, we can use singular homology; see (Reference Friedl, Nagel, Orson and Powell25, Appendix A). The cap product with the fundamental class
$(R,\mathbb {Z}[\pi _1(W)])$
-bimodule. As we mentioned above, if W does not admit a CW structure, we can use singular homology; see (Reference Friedl, Nagel, Orson and Powell25, Appendix A). The cap product with the fundamental class
![]() $[W, \partial W] \in H_{4}(W, \partial W)$
induces twisted Poincaré duality isomorphisms
$[W, \partial W] \in H_{4}(W, \partial W)$
induces twisted Poincaré duality isomorphisms
both of which we denote by
![]() $\text {PD}$
; for more details, we refer to (Reference Friedl, Nagel, Orson and Powell25, Appendix A).
$\text {PD}$
; for more details, we refer to (Reference Friedl, Nagel, Orson and Powell25, Appendix A).
In order to describe twisted intersection pairings, fix an
![]() $(R,R)$
-bimodule S and a non-singular
$(R,R)$
-bimodule S and a non-singular
![]() $\pi _1(W)$
-invariant sesquilinear pairing
$\pi _1(W)$
-invariant sesquilinear pairing
![]() $M \times M \to S$
. Compose the homomorphism induced by the inclusion
$M \times M \to S$
. Compose the homomorphism induced by the inclusion
![]() $(W,\emptyset ) \to (W,\partial W)$
with Poincaré duality and the evaluation homomorphism described above. The result is the following homomorphism of left R-modules:
$(W,\emptyset ) \to (W,\partial W)$
with Poincaré duality and the evaluation homomorphism described above. The result is the following homomorphism of left R-modules:
Restricting to the case where W is
![]() $2n$
-dimensional, the twisted intersection pairing
$2n$
-dimensional, the twisted intersection pairing
is defined by
![]() $\lambda _{M,W}(x,y)=\Phi (y)(x)$
. Note that while
$\lambda _{M,W}(x,y)=\Phi (y)(x)$
. Note that while
![]() $\lambda _{M,W}$
is
$\lambda _{M,W}$
is
![]() $(-1)^n$
-Hermitian, it may be singular: the submodule
$(-1)^n$
-Hermitian, it may be singular: the submodule
![]() $\operatorname {im} (H_{n}(\partial W;M) \to H_{n}(W;M)) $
is annihilated by
$\operatorname {im} (H_{n}(\partial W;M) \to H_{n}(W;M)) $
is annihilated by
![]() $\lambda _{M,W}$
, and the evaluation map need not be an isomorphism.
$\lambda _{M,W}$
, and the evaluation map need not be an isomorphism.
2.2 The twisted Blanchfield pairing
In this subsection, we review twisted Blanchfield pairings. While the construction can be performed over non-commutative rings [Reference Powell42, Reference Cochran, Orr and Teichner9, Reference Cochran8], we focus first on the case
![]() $R=\mathbb {F}[t^{\pm 1}]$
. References on twisted Blanchfield pairings include [Reference Miller and Powell40, Reference Powell42].
$R=\mathbb {F}[t^{\pm 1}]$
. References on twisted Blanchfield pairings include [Reference Miller and Powell40, Reference Powell42].
Let N be a closed
![]() $3$
-manifold. Just as in Example 2.1, let
$3$
-manifold. Just as in Example 2.1, let
![]() $\beta \colon \pi _1(N) \to GL_d({\mathbb {F}}[t^{\pm 1}])$
be a unitary representation and use
$\beta \colon \pi _1(N) \to GL_d({\mathbb {F}}[t^{\pm 1}])$
be a unitary representation and use
![]() $\mathbb {F}[t^{\pm 1}]^d_\beta $
to denote the
$\mathbb {F}[t^{\pm 1}]^d_\beta $
to denote the
![]() $({\mathbb {F}}[t^{\pm 1}],\mathbb {Z}[\pi _1(X)])$
-bimodule whose right
$({\mathbb {F}}[t^{\pm 1}],\mathbb {Z}[\pi _1(X)])$
-bimodule whose right
![]() $\mathbb {Z}[\pi _1(N)]$
-module structure is given by right multiplication by
$\mathbb {Z}[\pi _1(N)]$
-module structure is given by right multiplication by
![]() $\beta (\gamma )$
on row vectors. In what follows, we shall think of
$\beta (\gamma )$
on row vectors. In what follows, we shall think of
![]() $\mathbb {F}[t^{\pm 1}], \mathbb {F}(t)$
and
$\mathbb {F}[t^{\pm 1}], \mathbb {F}(t)$
and
![]() $\mathbb {F}(t)/\mathbb {F}[t^{\pm 1}]$
as
$\mathbb {F}(t)/\mathbb {F}[t^{\pm 1}]$
as
![]() $(\mathbb {F}[t^{\pm 1}],\mathbb {F}[t^{\pm 1}])$
-bimodules. Since
$(\mathbb {F}[t^{\pm 1}],\mathbb {F}[t^{\pm 1}])$
-bimodules. Since
are
![]() $(\mathbb {F}[t^{\pm 1}],\mathbb {Z}[\pi _1(N)])$
-bimodules, there is a short exact sequence
$(\mathbb {F}[t^{\pm 1}],\mathbb {Z}[\pi _1(N)])$
-bimodules, there is a short exact sequence
of cochain complexes of left
![]() $\mathbb {F}[t^{\pm 1}]$
-modules, where we identified
$\mathbb {F}[t^{\pm 1}]$
-modules, where we identified
![]() $\mathbb {F}[t^{\pm 1}]^d_\beta $
with
$\mathbb {F}[t^{\pm 1}]^d_\beta $
with
![]() $\mathbb {F}[t^{\pm 1}] \otimes _{{\mathbb {F}}[t^{\pm 1}]} \mathbb {F}[t^{\pm 1}]^d_\beta $
. Passing to cohomology, we obtain a long exact sequence in which the connecting map
$\mathbb {F}[t^{\pm 1}] \otimes _{{\mathbb {F}}[t^{\pm 1}]} \mathbb {F}[t^{\pm 1}]^d_\beta $
. Passing to cohomology, we obtain a long exact sequence in which the connecting map
is called the Bockstein homomorphism. We say that
![]() $\beta $
is
$\beta $
is
![]() $H_1$
-null if
$H_1$
-null if
![]() $H_1(N;\mathbb {F}(t)^{d}_{\beta })$
vanishes (i.e., if the
$H_1(N;\mathbb {F}(t)^{d}_{\beta })$
vanishes (i.e., if the
![]() ${\mathbb {F}}[t^{\pm 1}]$
-module
${\mathbb {F}}[t^{\pm 1}]$
-module
![]() $H_1(N;{\mathbb {F}}[t^{\pm 1}]_\beta ^d)$
is torsion). Observe that if
$H_1(N;{\mathbb {F}}[t^{\pm 1}]_\beta ^d)$
is torsion). Observe that if
![]() $\beta $
is
$\beta $
is
![]() $H_1$
-null, then the corresponding Bockstein homomorphism is an isomorphim: indeed, Poincaré duality and the universal coefficient theorem respectively imply that
$H_1$
-null, then the corresponding Bockstein homomorphism is an isomorphim: indeed, Poincaré duality and the universal coefficient theorem respectively imply that
![]() $H^2(N;\mathbb {F}(t)^d_\beta )$
and
$H^2(N;\mathbb {F}(t)^d_\beta )$
and
![]() $H^1(N;(\mathbb {F}(t) /\mathbb {F}[t^{\pm 1}])^d_\beta )$
vanish.
$H^1(N;(\mathbb {F}(t) /\mathbb {F}[t^{\pm 1}])^d_\beta )$
vanish.
Consider the composition
 $$ \begin{align*} \Theta \colon H_1(N;\mathbb{F}[t^{\pm 1}]^d_\beta) \, & \xrightarrow{PD}\, H^2(N;\mathbb{F}[t^{\pm 1}]^d_\beta) \\ & \xrightarrow{BS^{-1}} H^1(N;(\mathbb{F}(t)/\mathbb{F}[t^{\pm 1}])^d_\beta) \\ & \xrightarrow{\text{ev}} \operatorname{\mathrm{Hom}}_{\mathbb{F}[t^{\pm 1}]}(H_1(N;\mathbb{F}[t^{\pm 1}]^d_\beta),\mathbb{F}(t)/\mathbb{F}[t^{\pm 1}])^\# \end{align*} $$
$$ \begin{align*} \Theta \colon H_1(N;\mathbb{F}[t^{\pm 1}]^d_\beta) \, & \xrightarrow{PD}\, H^2(N;\mathbb{F}[t^{\pm 1}]^d_\beta) \\ & \xrightarrow{BS^{-1}} H^1(N;(\mathbb{F}(t)/\mathbb{F}[t^{\pm 1}])^d_\beta) \\ & \xrightarrow{\text{ev}} \operatorname{\mathrm{Hom}}_{\mathbb{F}[t^{\pm 1}]}(H_1(N;\mathbb{F}[t^{\pm 1}]^d_\beta),\mathbb{F}(t)/\mathbb{F}[t^{\pm 1}])^\# \end{align*} $$
of the three following
![]() $\mathbb {F}[t^{\pm 1}]$
-homomorphisms: Poincaré duality, the inverse Bocktein and the evaluation map described in Example 2.1. The main definition of this section is the following.
$\mathbb {F}[t^{\pm 1}]$
-homomorphisms: Poincaré duality, the inverse Bocktein and the evaluation map described in Example 2.1. The main definition of this section is the following.
Definition 2.2. Let N be a closed oriented
![]() $3$
-manifold and let
$3$
-manifold and let
![]() $\beta \colon \pi _1(N) \to GL_d(\mathbb {F}[t^{\pm 1}])$
be a unitary
$\beta \colon \pi _1(N) \to GL_d(\mathbb {F}[t^{\pm 1}])$
be a unitary
![]() $H_1$
-null representation. The twisted Blanchfield pairing associated to
$H_1$
-null representation. The twisted Blanchfield pairing associated to
![]() $\beta $
$\beta $
is defined as
![]() $\operatorname {\mathrm {Bl}}_\beta (N)(x,y)=\Theta (y)(x)$
. If
$\operatorname {\mathrm {Bl}}_\beta (N)(x,y)=\Theta (y)(x)$
. If
![]() $N=M_K$
is the
$N=M_K$
is the
![]() $0$
-framed surgery along a knot K, then we write
$0$
-framed surgery along a knot K, then we write
![]() $\operatorname {\mathrm {Bl}}_\beta (K)$
instead of
$\operatorname {\mathrm {Bl}}_\beta (K)$
instead of
![]() $\operatorname {\mathrm {Bl}}_\beta (M_K)$
.
$\operatorname {\mathrm {Bl}}_\beta (M_K)$
.
We refer to [Reference Powell42] for a more general treatment of twisted Blanchfield pairings but make two remarks nonetheless. First, Powell proved that
![]() $\operatorname {\mathrm {Bl}}_\beta (N)$
is Hermitian [Reference Powell42]. Second, since
$\operatorname {\mathrm {Bl}}_\beta (N)$
is Hermitian [Reference Powell42]. Second, since
![]() $\mathbb {F}[t^{\pm 1}]$
is a PID, it follows that
$\mathbb {F}[t^{\pm 1}]$
is a PID, it follows that
![]() $\operatorname {\mathrm {Bl}}_\beta (N)$
is non-singular: indeed,
$\operatorname {\mathrm {Bl}}_\beta (N)$
is non-singular: indeed,
![]() $\mathbb {F}(t)/\mathbb {F}[t^{\pm 1}]$
is an injective
$\mathbb {F}(t)/\mathbb {F}[t^{\pm 1}]$
is an injective
![]() $\mathbb {F}[t^{\pm 1}]$
-module, and thus, the evaluation map is an isomorphism.
$\mathbb {F}[t^{\pm 1}]$
-module, and thus, the evaluation map is an isomorphism.
Finally, although we mostly focus on closed 3-manifolds, we conclude this subsection with a remark on manifolds with boundary. To describe this case, we say that a representation
![]() $\beta \colon \pi _1(N) \to ~GL_d({\mathbb {F}}[t^{\pm 1}])$
is acyclic if
$\beta \colon \pi _1(N) \to ~GL_d({\mathbb {F}}[t^{\pm 1}])$
is acyclic if
![]() $H_i(N;\mathbb {F}[t^{\pm 1}]_\beta ^d)$
is a torsion
$H_i(N;\mathbb {F}[t^{\pm 1}]_\beta ^d)$
is a torsion
![]() $\mathbb {F}[t^{\pm 1}]$
-module for each i.
$\mathbb {F}[t^{\pm 1}]$
-module for each i.
Remark 2.3. If N is a 3-manifold with boundary and
![]() $\beta \colon \pi _1(N) \to GL_d({\mathbb {F}}[t^{\pm 1}])$
is a unitary acyclic representation, then one also obtains a twisted Blanchfield pairing
$\beta \colon \pi _1(N) \to GL_d({\mathbb {F}}[t^{\pm 1}])$
is a unitary acyclic representation, then one also obtains a twisted Blanchfield pairing
![]() $\operatorname {Bl}_\beta (N)$
. Indeed, one starts from the map
$\operatorname {Bl}_\beta (N)$
. Indeed, one starts from the map
![]() $i \colon H_1(N;{\mathbb {F}}[t^{\pm 1}]_\beta ^d) \to H_1(N,\partial N;{\mathbb {F}}[t^{\pm 1}]_\beta ^d)$
induced by the inclusion
$i \colon H_1(N;{\mathbb {F}}[t^{\pm 1}]_\beta ^d) \to H_1(N,\partial N;{\mathbb {F}}[t^{\pm 1}]_\beta ^d)$
induced by the inclusion
![]() $(N,\emptyset ) \to ~(N,\partial N)$
and then proceeds as in the closed case, using duality, the inverse of the Bockstein homorphism and evaluation. The acyclicity assumption is used to guarantee that the Bockstein homomorphism is an isomorphism:
$(N,\emptyset ) \to ~(N,\partial N)$
and then proceeds as in the closed case, using duality, the inverse of the Bockstein homorphism and evaluation. The acyclicity assumption is used to guarantee that the Bockstein homomorphism is an isomorphism:
![]() $H_1$
-nullity is not enough when the boundary is nonempty, although an alternative is to work on the torsion submodule of
$H_1$
-nullity is not enough when the boundary is nonempty, although an alternative is to work on the torsion submodule of
![]() $H_1(N;{\mathbb {F}}[t^{\pm 1}]_\beta ^d)$
and to proceed as in [Reference Hillman29, Reference Powell42] or [Reference Conway12, Subsection 2.2]. Finally, note that when
$H_1(N;{\mathbb {F}}[t^{\pm 1}]_\beta ^d)$
and to proceed as in [Reference Hillman29, Reference Powell42] or [Reference Conway12, Subsection 2.2]. Finally, note that when
![]() $\partial N$
is nonempty,
$\partial N$
is nonempty,
![]() $\operatorname {Bl}_\beta (N)$
may be singular: the map i need not be an isomorphism.
$\operatorname {Bl}_\beta (N)$
may be singular: the map i need not be an isomorphism.
2.3 Relation to Blanchfield pairings over noncommutative rings
Twisted Blanchfield pairing are also defined in the non-commutative setting, using Ore rings [Reference Cochran, Orr and Teichner9, Reference Friedl, Leidy, Nagel and Powell21, Reference Powell42]. In this subsection, after briefly reviewing some basics on these rings, we relate the resulting non-commutative Blanchfield pairings to the twisted Blanchfield pairings of Subsection 2.2. The reason for this incursion into the non-commutative setting is that the proof of Theorem 3.11 requires that we import a result from [Reference Friedl, Leidy, Nagel and Powell21] (which uses non-commutative Blanchfield forms) into the setting of twisted Blanchfield forms.
We start with some brief recollections on Ore rings, referring to [Reference Lam31, Chapter 4, Section 10] for further details. Let
![]() $\mathcal {R}$
be a ring. A multiplicative subset
$\mathcal {R}$
be a ring. A multiplicative subset
![]() $S \subset \mathcal {R}$
is right permutable if, for any
$S \subset \mathcal {R}$
is right permutable if, for any
![]() $r \in \mathcal {R}$
and
$r \in \mathcal {R}$
and
![]() $s \in S$
, we have
$s \in S$
, we have
![]() $r S \cap s\mathcal {R} \neq \emptyset $
. An element
$r S \cap s\mathcal {R} \neq \emptyset $
. An element
![]() $r \in \mathcal {R}$
is regular if it is neither a left zero divisor nor a right zero divisor. We say that
$r \in \mathcal {R}$
is regular if it is neither a left zero divisor nor a right zero divisor. We say that
![]() $\mathcal {R}$
is a right Ore ring if the set S of regular elements is right permutable. In this case,
$\mathcal {R}$
is a right Ore ring if the set S of regular elements is right permutable. In this case,
![]() $\mathcal {R}$
can be localized at S, and
$\mathcal {R}$
can be localized at S, and
![]() $\mathcal {R}S^{-1}$
is called the right ring of quotients of
$\mathcal {R}S^{-1}$
is called the right ring of quotients of
![]() $\mathcal {R}$
. The left analogues of these notions are defined similarly. If
$\mathcal {R}$
. The left analogues of these notions are defined similarly. If
![]() $\mathcal {R}$
is both a left Ore ring and a right Ore ring, then
$\mathcal {R}$
is both a left Ore ring and a right Ore ring, then
![]() $\mathcal {R}$
is called an Ore ring. In this case, the right and left rings of quotients agree, and we simply write
$\mathcal {R}$
is called an Ore ring. In this case, the right and left rings of quotients agree, and we simply write
![]() $\mathcal {Q}$
.
$\mathcal {Q}$
.
Commutative rings are Ore rings [Reference Lam31, Chapter 4, Section 10, 10.18]. In what follows, however, we shall mostly be concerned with rings of matrices.
Example 2.4. If R is a commutative ring, then the matrix ring
![]() $\mathcal {M}_{d}(R)$
is an Ore ring [Reference Lam31, Example 11.21(1)]. For concreteness, we focus on the case where
$\mathcal {M}_{d}(R)$
is an Ore ring [Reference Lam31, Example 11.21(1)]. For concreteness, we focus on the case where
![]() $R={\mathbb {F}}[t^{\pm 1}]$
. In this case, by [Reference Lam31, Example 11.21(1)] and [Reference Lam31, Proposition 10.21], the ring of quotients of
$R={\mathbb {F}}[t^{\pm 1}]$
. In this case, by [Reference Lam31, Example 11.21(1)] and [Reference Lam31, Proposition 10.21], the ring of quotients of
![]() $\mathcal {M}_{d}(\mathbb {F}[t^{\pm 1}])$
is isomorphic to
$\mathcal {M}_{d}(\mathbb {F}[t^{\pm 1}])$
is isomorphic to
![]() $\mathcal {M}_{d}(\mathbb {F}(t))$
.
$\mathcal {M}_{d}(\mathbb {F}(t))$
.
Next, suppose that R is a commutative ring with unit. Right multiplication on row vectors endows
![]() $R^{d}$
with a right
$R^{d}$
with a right
![]() $\mathcal {M}_{d}(R)$
-module structure. We write
$\mathcal {M}_{d}(R)$
-module structure. We write
![]() $R^{d}_{\mathcal {M}}$
for emphasis. An alternate description of
$R^{d}_{\mathcal {M}}$
for emphasis. An alternate description of
![]() $R^{d}_{\mathcal {M}}$
is obtained by considering the elementary matrix
$R^{d}_{\mathcal {M}}$
is obtained by considering the elementary matrix
![]() $E_{i,j}$
whose only nonzero coefficient is a
$E_{i,j}$
whose only nonzero coefficient is a
![]() $1$
in its
$1$
in its
![]() $(i,j)$
-entry. Indeed, one has the isomorphim
$(i,j)$
-entry. Indeed, one has the isomorphim
![]() $ E_{i,i}\mathcal {M}_d(R) \cong R^{d}_{\mathcal {M}}$
of right
$ E_{i,i}\mathcal {M}_d(R) \cong R^{d}_{\mathcal {M}}$
of right
![]() $\mathcal {M}_d(R)$
-modules.
$\mathcal {M}_d(R)$
-modules.
The next lemma shows that
![]() $\mathcal {M}_d(R)$
decomposes as a direct sum of d copies of
$\mathcal {M}_d(R)$
decomposes as a direct sum of d copies of
![]() $R^{d}_{\mathcal {M}}$
.
$R^{d}_{\mathcal {M}}$
.
Lemma 2.5. If R is a commutative ring with unit, then
![]() $R^{d}_{\mathcal {M}}$
is a projective right
$R^{d}_{\mathcal {M}}$
is a projective right
![]() $\mathcal {M}_{d}(R)$
-module. In fact, we have the following isomorphism of right
$\mathcal {M}_{d}(R)$
-module. In fact, we have the following isomorphism of right
![]() $\mathcal {M}_{d}(R)$
-modules:
$\mathcal {M}_{d}(R)$
-modules:
 $$ \begin{align} \mathcal{M}_{d}(R) \cong \bigoplus_{i=1}^d E_{i,i}\mathcal{M}_{d}(R) \cong \bigoplus_{i=1}^d R^{d}_{\mathcal{M}}. \end{align} $$
$$ \begin{align} \mathcal{M}_{d}(R) \cong \bigoplus_{i=1}^d E_{i,i}\mathcal{M}_{d}(R) \cong \bigoplus_{i=1}^d R^{d}_{\mathcal{M}}. \end{align} $$
Proof. First, notice that the
![]() $E_{i,i}$
are orthogonal idempotents: one has
$E_{i,i}$
are orthogonal idempotents: one has
![]() $E_{i,i} E_{j,j}=\delta _{ij}E_{i,j}$
. The conclusion of the lemma now follows since
$E_{i,i} E_{j,j}=\delta _{ij}E_{i,j}$
. The conclusion of the lemma now follows since
![]() $\operatorname {id} = E_{1,1} + \cdots +E_{d,d}$
.
$\operatorname {id} = E_{1,1} + \cdots +E_{d,d}$
.
Next, assume that X is a CW complex together with a homomorphism
![]() $\gamma \colon \mathbb {Z}[\pi _1(X)] \to \mathcal {R}$
to an Ore ring
$\gamma \colon \mathbb {Z}[\pi _1(X)] \to \mathcal {R}$
to an Ore ring
![]() $\mathcal {R}$
. Just as in Subsection 2.1, this endows
$\mathcal {R}$
. Just as in Subsection 2.1, this endows
![]() $\mathcal {R}$
with a right
$\mathcal {R}$
with a right
![]() $\mathbb {Z}[\pi _1(X)]$
-module structure which we denote by
$\mathbb {Z}[\pi _1(X)]$
-module structure which we denote by
![]() $\mathcal {R}_\gamma $
for emphasis. Given a commutative ring R with unit, note that any representation
$\mathcal {R}_\gamma $
for emphasis. Given a commutative ring R with unit, note that any representation
![]() $\gamma \colon \pi _{1}(X) \to GL_d(R)$
canonically extends to a ring homomorphism
$\gamma \colon \pi _{1}(X) \to GL_d(R)$
canonically extends to a ring homomorphism
![]() $\gamma \colon \mathbb {Z}[\pi _{1}(X)] \to \mathcal {M}_{d}(R)$
. In particular,
$\gamma \colon \mathbb {Z}[\pi _{1}(X)] \to \mathcal {M}_{d}(R)$
. In particular,
![]() $\gamma $
endows
$\gamma $
endows
![]() $R^d$
and
$R^d$
and
![]() $\mathcal {R}=\mathcal {M}_d(R)$
with right
$\mathcal {R}=\mathcal {M}_d(R)$
with right
![]() $\mathbb {Z}[\pi _{1}(X)]$
-module structures.
$\mathbb {Z}[\pi _{1}(X)]$
-module structures.
The following proposition is a topological application of Lemma 2.5.
Proposition 2.6. Let R be a commutative ring with unit. If
![]() $\gamma \colon \pi _1(X) \to GL_d(R)$
is a representation, then we have the following chain isomorphisms of chain complexes of left R-modules:
$\gamma \colon \pi _1(X) \to GL_d(R)$
is a representation, then we have the following chain isomorphisms of chain complexes of left R-modules:
 $$ \begin{align*} & C_*(X;\mathcal{M}_d(R)_\gamma) \cong \bigoplus_{i=1}^d C_*(X;R_\gamma^d), \\ &C^*(X;\mathcal{M}_d(R)_\gamma) \cong \bigoplus_{i=1}^d C^*(X;R_\gamma^d). \end{align*} $$
$$ \begin{align*} & C_*(X;\mathcal{M}_d(R)_\gamma) \cong \bigoplus_{i=1}^d C_*(X;R_\gamma^d), \\ &C^*(X;\mathcal{M}_d(R)_\gamma) \cong \bigoplus_{i=1}^d C^*(X;R_\gamma^d). \end{align*} $$
Furthermore, one also has the following isomorphisms of left R-modules:
 $$ \begin{align*} & H_*(X;R_\gamma^d) \cong R^d_{\mathcal{M}} \otimes_{\mathcal{M}_d(R)} H_*(X;\mathcal{M}_d(R)_\gamma) , \\ & H^*(X;R_\gamma^d) \cong R^d_{\mathcal{M}} \otimes_{\mathcal{M}_d(R)} H^*(X;\mathcal{M}_d(R)_\gamma). \end{align*} $$
$$ \begin{align*} & H_*(X;R_\gamma^d) \cong R^d_{\mathcal{M}} \otimes_{\mathcal{M}_d(R)} H_*(X;\mathcal{M}_d(R)_\gamma) , \\ & H^*(X;R_\gamma^d) \cong R^d_{\mathcal{M}} \otimes_{\mathcal{M}_d(R)} H^*(X;\mathcal{M}_d(R)_\gamma). \end{align*} $$
Proof. The chain isomorphisms follow from the decomposition of
![]() $\mathcal {M}_d(R)$
displayed in (2.1). To deal with the second assertion, we once again use Lemma 2.5 to deduce that
$\mathcal {M}_d(R)$
displayed in (2.1). To deal with the second assertion, we once again use Lemma 2.5 to deduce that
![]() $\mathcal {M}_d(R)$
is a projective (and thus flat)
$\mathcal {M}_d(R)$
is a projective (and thus flat)
![]() $R_{\mathcal {M}}^d$
-module. We therefore obtain the following isomorphisms:
$R_{\mathcal {M}}^d$
-module. We therefore obtain the following isomorphisms:
The proof for cohomology is analogous. This concludes the proof of the lemma.
Next, we deal with non-commutative Blanchfield pairings. Let N be a closed oriented
![]() $3$
-manifold. Let
$3$
-manifold. Let
![]() $\mathcal {R}$
be an Ore ring with involution and use
$\mathcal {R}$
be an Ore ring with involution and use
![]() $\mathcal {Q}$
to denote its ring of quotients. Given a homomorphism
$\mathcal {Q}$
to denote its ring of quotients. Given a homomorphism
![]() $\gamma \colon \mathbb {Z}[\pi _1(N)] \to \mathcal {R}$
, we can view
$\gamma \colon \mathbb {Z}[\pi _1(N)] \to \mathcal {R}$
, we can view
![]() $\mathcal {R},\mathcal {Q}$
and
$\mathcal {R},\mathcal {Q}$
and
![]() $\mathcal {Q}/\mathcal {R}$
as right
$\mathcal {Q}/\mathcal {R}$
as right
![]() $\mathbb {Z}[\pi _1(N)]$
-modules. In particular, as in Subsections 2.1 and 2.2, there are Poincaré duality isomorphisms and a Bockstein homomorphism on cohomology. Thus, if
$\mathbb {Z}[\pi _1(N)]$
-modules. In particular, as in Subsections 2.1 and 2.2, there are Poincaré duality isomorphisms and a Bockstein homomorphism on cohomology. Thus, if
![]() $H_1(N;\mathcal {Q}_\gamma )=0$
, then one can consider the composition
$H_1(N;\mathcal {Q}_\gamma )=0$
, then one can consider the composition
We refer to [Reference Friedl, Leidy, Nagel and Powell21, Section 2] for further details, but the upshot is that there is a Blanchfield pairing in the non-commutative setting which is defined exactly as in Subsection 2.2.
Definition 2.7. Let N be a closed oriented
![]() $3$
-manifold together with a map
$3$
-manifold together with a map
![]() $\gamma \colon \mathbb {Z}[\pi _1(N)] \to \mathcal {R}$
to an Ore ring with involution. Assuming that
$\gamma \colon \mathbb {Z}[\pi _1(N)] \to \mathcal {R}$
to an Ore ring with involution. Assuming that
![]() $H_1(N;\mathcal {Q}_\gamma )=0$
, there is a non-commutative Blanchfield pairing
$H_1(N;\mathcal {Q}_\gamma )=0$
, there is a non-commutative Blanchfield pairing
which is defined by setting
![]() $\operatorname {\mathrm {Bl}}_{\mathcal {R},\gamma }(N)(x,y)=\Phi (y)(x)$
.
$\operatorname {\mathrm {Bl}}_{\mathcal {R},\gamma }(N)(x,y)=\Phi (y)(x)$
.
Note that in the literature
![]() $\mathcal {R}$
, is usually assumed to be an Ore domain; however, the definition extends verbatim to the case of Ore rings. The next proposition relates the non-commutative Blanchfield pairing to the twisted Blanchfield pairing.
$\mathcal {R}$
, is usually assumed to be an Ore domain; however, the definition extends verbatim to the case of Ore rings. The next proposition relates the non-commutative Blanchfield pairing to the twisted Blanchfield pairing.
Proposition 2.8. Let N be a closed oriented
![]() $3$
-manifold and let
$3$
-manifold and let
![]() $\gamma \colon \pi _{1}(N) \to GL_d({\mathbb {F}}[t^{\pm 1}])$
be a representation. The following assertions hold:
$\gamma \colon \pi _{1}(N) \to GL_d({\mathbb {F}}[t^{\pm 1}])$
be a representation. The following assertions hold:
-
(1) We have
 $H_*(N;\mathbb {F}(t)^d_\gamma )=0$
if and only if
$H_*(N;\mathbb {F}(t)^d_\gamma )=0$
if and only if
 $H_*(N;\mathcal {M}_{d}(\mathbb {F}(t))_\gamma )=0$
.
$H_*(N;\mathcal {M}_{d}(\mathbb {F}(t))_\gamma )=0$
. -
(2) The following
 ${\mathbb {F}}[t^{\pm 1}]$
-linking forms are canonically isometric:
${\mathbb {F}}[t^{\pm 1}]$
-linking forms are canonically isometric:  $$\begin{align*}\mathbb{F}[t^{\pm1}]^{d}_{\mathcal{M}} \otimes_{\mathcal{M}_{d}(\mathbb{F}[t^{\pm1}])} \operatorname{\mathrm{Bl}}_{\mathcal{M}_{d}(\mathbb{F}[t^{\pm1}]),\gamma}(N) \cong \operatorname{\mathrm{Bl}}_{\gamma}(N).\end{align*}$$
$$\begin{align*}\mathbb{F}[t^{\pm1}]^{d}_{\mathcal{M}} \otimes_{\mathcal{M}_{d}(\mathbb{F}[t^{\pm1}])} \operatorname{\mathrm{Bl}}_{\mathcal{M}_{d}(\mathbb{F}[t^{\pm1}]),\gamma}(N) \cong \operatorname{\mathrm{Bl}}_{\gamma}(N).\end{align*}$$
Proof. The first assertion follows immediately from the first assertion of Proposition 2.6. Next, we deal with the second assertion. Using once again the first assertion of Proposition 2.6, the linking form
![]() $\operatorname {\mathrm {Bl}}_{\mathcal {M}_d({\mathbb {F}}[t^{\pm 1}]),\gamma }(N)$
can canonically be thought of as a linking form
$\operatorname {\mathrm {Bl}}_{\mathcal {M}_d({\mathbb {F}}[t^{\pm 1}]),\gamma }(N)$
can canonically be thought of as a linking form
 $$ \begin{align*}\operatorname{\mathrm{Bl}}_{\mathcal{M}_d({\mathbb{F}}[t^{\pm 1}]),\gamma}(N) \colon \bigoplus_{i=1}^d H_1(N;{\mathbb{F}}[t^{\pm 1}]_\gamma^d) \times \bigoplus_{i=1}^d H_1(N;{\mathbb{F}}[t^{\pm 1}]_\gamma^d) \to \mathcal{M}_d(\mathbb{F}(t))/\mathcal{M}_d({\mathbb{F}}[t^{\pm 1}]),\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Bl}}_{\mathcal{M}_d({\mathbb{F}}[t^{\pm 1}]),\gamma}(N) \colon \bigoplus_{i=1}^d H_1(N;{\mathbb{F}}[t^{\pm 1}]_\gamma^d) \times \bigoplus_{i=1}^d H_1(N;{\mathbb{F}}[t^{\pm 1}]_\gamma^d) \to \mathcal{M}_d(\mathbb{F}(t))/\mathcal{M}_d({\mathbb{F}}[t^{\pm 1}]),\end{align*} $$
where the above decomposition is obtained by using the matrices
![]() $E_{i,i}$
, for
$E_{i,i}$
, for
![]() $1 \leq i \leq d$
. The result now follows by tensoring with
$1 \leq i \leq d$
. The result now follows by tensoring with
![]() ${\mathbb {F}}[t^{\pm 1}]_{\mathcal {M}}^d$
and using the second assertion of Proposition 2.6. Indeed, both Blanchfield pairings are defined by composing Poincaré duality isomorphisms, inverse Bockstein isomorphisms and evaluation maps. The first two maps preserve the direct sum decomposition displayed above. After applying the adjoint of evaluation map, and using the identification from Proposition 2.6,
${\mathbb {F}}[t^{\pm 1}]_{\mathcal {M}}^d$
and using the second assertion of Proposition 2.6. Indeed, both Blanchfield pairings are defined by composing Poincaré duality isomorphisms, inverse Bockstein isomorphisms and evaluation maps. The first two maps preserve the direct sum decomposition displayed above. After applying the adjoint of evaluation map, and using the identification from Proposition 2.6,
![]() $\operatorname {\mathrm {Bl}}_{\mathcal {M}_d({\mathbb {F}}[t^{\pm 1}])}$
is given by
$\operatorname {\mathrm {Bl}}_{\mathcal {M}_d({\mathbb {F}}[t^{\pm 1}])}$
is given by
for
![]() $x,y \in H_{1}(N;{\mathbb {F}}[t^{\pm 1}]^{d}_{\gamma })$
. This concludes the proof of the proposition.
$x,y \in H_{1}(N;{\mathbb {F}}[t^{\pm 1}]^{d}_{\gamma })$
. This concludes the proof of the proposition.
Informally, Proposition 2.8 implies that several statements that hold for non-commutative Blanchfield pairings also hold for twisted Blanchfield pairings. This will be used in Theorem 3.11.
3 Twisted signatures of 3-manifolds and knots
This section is organized as follows. In Subsection 3.1, we introduce our twisted signature function and describe its basic properties, in Subsection 3.2, we provide conditions for its bordism invariance and in Subsection 3.3, we investigate its behavior under satellite operations.
3.1 Definition of the twisted signatures
In this short subsection, we define our twisted signature invariants for knots and 3-manifolds. To this effect, recall that Proposition 1.6 associated to a linking form
![]() $(M,\lambda )$
a locally constant functions
$(M,\lambda )$
a locally constant functions
![]() $\sigma _{(M,\lambda )} \colon S^1 \to \mathbb {Z} $
and
$\sigma _{(M,\lambda )} \colon S^1 \to \mathbb {Z} $
and
![]() $\sigma _{(M,\lambda )}^{av} \colon S^1 \to \mathbb {Z}$
with desirable properties.
$\sigma _{(M,\lambda )}^{av} \colon S^1 \to \mathbb {Z}$
with desirable properties.
Definition 3.1. Let N be a closed connected oriented
![]() $3$
-manifold and let
$3$
-manifold and let
![]() $\beta \colon \pi _1(N) \to GL_d(\mathbb {F}[t^{\pm 1}])$
be a unitary
$\beta \colon \pi _1(N) \to GL_d(\mathbb {F}[t^{\pm 1}])$
be a unitary
![]() $H_1$
-null representation. The twisted signature function
$H_1$
-null representation. The twisted signature function
![]() $\sigma _{N,\beta } \colon S^1 \to \mathbb {Z}$
of the pair
$\sigma _{N,\beta } \colon S^1 \to \mathbb {Z}$
of the pair
![]() $(N,\beta )$
is the signature function of the non-singular linking form
$(N,\beta )$
is the signature function of the non-singular linking form
![]() $\operatorname {\mathrm {Bl}}_\beta (N)$
. The averaged signature function
$\operatorname {\mathrm {Bl}}_\beta (N)$
. The averaged signature function
![]() $\sigma _{N,\beta }^{\operatorname {av}}$
is the averaged signature function of
$\sigma _{N,\beta }^{\operatorname {av}}$
is the averaged signature function of
![]() $\operatorname {\mathrm {Bl}}_\beta (N)$
.
$\operatorname {\mathrm {Bl}}_\beta (N)$
.
The corresponding invariants for a knot K are obtained by applying Definition 3.1 to the 0-framed surgery
![]() $M_K$
.
$M_K$
.
Definition 3.2. Let K be an oriented knot and let
![]() $\beta \colon \pi _1(M_K) \to GL_d(\mathbb {F}[t^{\pm 1}])$
be a unitary
$\beta \colon \pi _1(M_K) \to GL_d(\mathbb {F}[t^{\pm 1}])$
be a unitary
![]() $H_1$
-null representation. The twisted signature function
$H_1$
-null representation. The twisted signature function
![]() $\sigma _{K,\beta }\colon S^1\to \mathbb {Z}$
of K is the twisted signature function of
$\sigma _{K,\beta }\colon S^1\to \mathbb {Z}$
of K is the twisted signature function of
![]() $M_K$
, and similarly for the averaged signature function
$M_K$
, and similarly for the averaged signature function
![]() $ \sigma _{K,\beta }^{\operatorname {av}}$
.
$ \sigma _{K,\beta }^{\operatorname {av}}$
.
Before proving properties, we show how Definition 3.2 recovers the Levine-Tristram signature. This establishes the fourth property of Theorem 1.1 from the introduction.
Remark 3.3. If
![]() $\beta $
is the abelianization map
$\beta $
is the abelianization map
![]() $\phi _K$
, then
$\phi _K$
, then
![]() $\operatorname {\mathrm {Bl}}_\beta (K)$
coincides with the untwisted Blanchfield pairing
$\operatorname {\mathrm {Bl}}_\beta (K)$
coincides with the untwisted Blanchfield pairing
![]() $\operatorname {Bl}(K)$
, and the corresponding signature function recovers the Levine-Tristram signature
$\operatorname {Bl}(K)$
, and the corresponding signature function recovers the Levine-Tristram signature
![]() $\sigma _K$
thanks to [Reference Borodzik and Friedl4, Lemma 3.2]. Note that
$\sigma _K$
thanks to [Reference Borodzik and Friedl4, Lemma 3.2]. Note that
![]() $\operatorname {Bl}(K)$
is usually defined on the Alexander module
$\operatorname {Bl}(K)$
is usually defined on the Alexander module
![]() $H_1(X_K;{\mathbb {F}}[t^{\pm 1}])$
, where
$H_1(X_K;{\mathbb {F}}[t^{\pm 1}])$
, where
![]() $X_K=S^3 \setminus \mathcal {N}(K)$
is the complement of a tubular neighborhood
$X_K=S^3 \setminus \mathcal {N}(K)$
is the complement of a tubular neighborhood
![]() $\mathcal {N}(K)$
of K in
$\mathcal {N}(K)$
of K in
![]() $S^3$
. It is, however, well known that the inclusion
$S^3$
. It is, however, well known that the inclusion
![]() $X_K \hookrightarrow M_K$
induces a Blanchfield form preserving isomorphism
$X_K \hookrightarrow M_K$
induces a Blanchfield form preserving isomorphism
![]() $H_1(X_K;{\mathbb {F}}[t^{\pm 1}]) \cong H_1(M_K;{\mathbb {F}}[t^{\pm 1}])$
.
$H_1(X_K;{\mathbb {F}}[t^{\pm 1}]) \cong H_1(M_K;{\mathbb {F}}[t^{\pm 1}])$
.
Contrarily to
![]() $\sigma _K$
, the twisted signature function
$\sigma _K$
, the twisted signature function
![]() $\sigma _{K,\beta }$
is not known to be symmetric (i.e.,
$\sigma _{K,\beta }$
is not known to be symmetric (i.e.,
![]() $\sigma _{K,\beta }(\overline {\omega })$
is not known to equal
$\sigma _{K,\beta }(\overline {\omega })$
is not known to equal
![]() $\sigma _{K,\beta }(\omega )$
). More precisely, in [Reference Borodzik, Conway and Politarczyk3], we show that signature functions associated to abstract linking forms over
$\sigma _{K,\beta }(\omega )$
). More precisely, in [Reference Borodzik, Conway and Politarczyk3], we show that signature functions associated to abstract linking forms over
![]() ${\mathbb {C}}[t^{\pm 1}]$
are not symmetric, but it remains unknown whether such linking forms can be realized as twisted Blanchfield forms. Despite this difference, the next proposition shows that the twisted signature shares several properties with its classical counterpart. This establishes the first item of Theorem 1.1 from the introduction.
${\mathbb {C}}[t^{\pm 1}]$
are not symmetric, but it remains unknown whether such linking forms can be realized as twisted Blanchfield forms. Despite this difference, the next proposition shows that the twisted signature shares several properties with its classical counterpart. This establishes the first item of Theorem 1.1 from the introduction.
Proposition 3.4. Let K be an oriented knot and let
![]() $\beta \colon \pi _1(M_K) \to GL_d(\mathbb {F}[t^{\pm 1}])$
be a unitary
$\beta \colon \pi _1(M_K) \to GL_d(\mathbb {F}[t^{\pm 1}])$
be a unitary
![]() $H_1$
-null representation.
$H_1$
-null representation.
-
(1) The twisted signature
 $\sigma _{K,\beta }$
is constant on the complement in
$\sigma _{K,\beta }$
is constant on the complement in
 $S^1$
of the zero set of the twisted Alexander polynomial
$S^1$
of the zero set of the twisted Alexander polynomial
 $\Delta _{M_K}^\beta (t):=\operatorname {Ord}(H_1(M_K;\mathbb {F}[t^{\pm 1}]_\beta ^d))$
.
$\Delta _{M_K}^\beta (t):=\operatorname {Ord}(H_1(M_K;\mathbb {F}[t^{\pm 1}]_\beta ^d))$
. -
(2) Let
 $\overline {K}$
denote the mirror image of K. The representation
$\overline {K}$
denote the mirror image of K. The representation
 $\beta $
canonically defines a representation on
$\beta $
canonically defines a representation on
 $\pi _1(M_{\overline {K}})$
(which we also denote by
$\pi _1(M_{\overline {K}})$
(which we also denote by
 $\beta $
) and, for all
$\beta $
) and, for all
 $\omega \in S^1$
, we have
$\omega \in S^1$
, we have  $$ \begin{align*} &\operatorname{\mathrm{Bl}}_\beta(\overline{K})=-\operatorname{\mathrm{Bl}}_\beta(K), \\ &\sigma_{\overline{K},\beta}=-\sigma_{K,\beta}. \end{align*} $$
$$ \begin{align*} &\operatorname{\mathrm{Bl}}_\beta(\overline{K})=-\operatorname{\mathrm{Bl}}_\beta(K), \\ &\sigma_{\overline{K},\beta}=-\sigma_{K,\beta}. \end{align*} $$
-
(3) Let
 $K^r$
denote K with its orientation reversed. Assume that
$K^r$
denote K with its orientation reversed. Assume that
 $\beta (g)=\phi _K(g)\rho (g)$
, where
$\beta (g)=\phi _K(g)\rho (g)$
, where
 $\rho \colon \pi _1(M_K) \to GL_n(\mathbb {F})$
is a unitary representation. The representation
$\rho \colon \pi _1(M_K) \to GL_n(\mathbb {F})$
is a unitary representation. The representation
 $\beta $
canonically defines a representation on
$\beta $
canonically defines a representation on
 $\pi _1(M_{K^r})$
(which we also denote by
$\pi _1(M_{K^r})$
(which we also denote by
 $\beta $
) and, for all
$\beta $
) and, for all
 $\omega \in S^1$
, we have
$\omega \in S^1$
, we have  $$ \begin{align*} & \operatorname{\mathrm{Bl}}_{\beta}(K^r)(t) =\operatorname{\mathrm{Bl}}_{\beta}(K^r)(t^{-1}) , \\ & \sigma_{K^r,\beta}(\omega) =\sigma_{K,\beta}(\overline{\omega}). \end{align*} $$
$$ \begin{align*} & \operatorname{\mathrm{Bl}}_{\beta}(K^r)(t) =\operatorname{\mathrm{Bl}}_{\beta}(K^r)(t^{-1}) , \\ & \sigma_{K^r,\beta}(\omega) =\sigma_{K,\beta}(\overline{\omega}). \end{align*} $$
Proof. The proof of the first property follows by applying item (S-1) of Proposition 1.6 to the twisted Blanchfield pairing. To prove the second assertion, let
![]() $h \colon S^3 \to S^3$
be an orientation reversing homeomorphism such that
$h \colon S^3 \to S^3$
be an orientation reversing homeomorphism such that
![]() $h(K)=\overline {K}$
. Note that h induces an orientation reversion homeomorphism
$h(K)=\overline {K}$
. Note that h induces an orientation reversion homeomorphism
![]() $h \colon M_K \to M_{\overline {K}}$
. A diagram chase involving the definition of the Blanchfield pairing now shows that h induces an isometry
$h \colon M_K \to M_{\overline {K}}$
. A diagram chase involving the definition of the Blanchfield pairing now shows that h induces an isometry
![]() $\operatorname {\mathrm {Bl}}_\beta (\overline {K})\cong -\operatorname {\mathrm {Bl}}_\beta (K)$
, the key point being that the square involving Poincaré duality anti-commutes thanks to the identity
$\operatorname {\mathrm {Bl}}_\beta (\overline {K})\cong -\operatorname {\mathrm {Bl}}_\beta (K)$
, the key point being that the square involving Poincaré duality anti-commutes thanks to the identity
![]() $h_*(h^*(\xi ) \cap [M_K])=\xi \cap h_*([M_K])=-\xi \cap [M_{\overline {K}}]$
for any
$h_*(h^*(\xi ) \cap [M_K])=\xi \cap h_*([M_K])=-\xi \cap [M_{\overline {K}}]$
for any
![]() $\xi \in H^2(M_K;{\mathbb {F}}[t^{\pm 1}]^n_\beta )$
. The result on the signature now follows from the definition. The third assertion is a consequence of the identity
$\xi \in H^2(M_K;{\mathbb {F}}[t^{\pm 1}]^n_\beta )$
. The result on the signature now follows from the definition. The third assertion is a consequence of the identity
![]() $\phi _K(\mu _{K^r})=\phi _K(\mu _K)^{-1}$
.
$\phi _K(\mu _{K^r})=\phi _K(\mu _K)^{-1}$
.
The order of
![]() $H_1(M_K;\mathbb {F}[t^{\pm 1}]_\beta ^d)$
can be related to the twisted Alexander polynomial of K which is usually defined on the exterior
$H_1(M_K;\mathbb {F}[t^{\pm 1}]_\beta ^d)$
can be related to the twisted Alexander polynomial of K which is usually defined on the exterior
![]() $X_K$
of K; see [Reference Kirk and Livingston30, Lemma 6.3] and [Reference Friedl and Vidussi24, Lemma 3]. In the abelian case, since
$X_K$
of K; see [Reference Kirk and Livingston30, Lemma 6.3] and [Reference Friedl and Vidussi24, Lemma 3]. In the abelian case, since
![]() $H_1(M_K;{\mathbb {F}}[t^{\pm 1}]) \cong H_1(X_K;{\mathbb {F}}[t^{\pm 1}])$
, the first item of Proposition 3.4 (and Remark 3.3) recovers the well-known fact that the Levine-Tristram signature function
$H_1(M_K;{\mathbb {F}}[t^{\pm 1}]) \cong H_1(X_K;{\mathbb {F}}[t^{\pm 1}])$
, the first item of Proposition 3.4 (and Remark 3.3) recovers the well-known fact that the Levine-Tristram signature function
![]() $\sigma _K$
is constant on the complement of the zero set of the Alexander polynomial
$\sigma _K$
is constant on the complement of the zero set of the Alexander polynomial
![]() $\Delta _K(t)$
. The second item of Proposition 3.4 is also a direct generalization of the corresponding property for the Levine-Tristram signature.
$\Delta _K(t)$
. The second item of Proposition 3.4 is also a direct generalization of the corresponding property for the Levine-Tristram signature.
Remark 3.5. Since the Levine-Tristram is symmetric, it satisfies
![]() $\sigma _{K^r}(\omega )=\sigma _{K}(\omega )$
. This does not appear to be the case in general since the signature function of a general complex linking form need not be symmetric.
$\sigma _{K^r}(\omega )=\sigma _{K}(\omega )$
. This does not appear to be the case in general since the signature function of a general complex linking form need not be symmetric.
Motivated by Remark 3.3 and Proposition 3.4, the next subsections investigate to what extent the properties of the Levine-Tristram signature generalize to our twisted signatures.
3.2 Bordism and concordance invariance
In this subsection, we give conditions under which the signatures of 3-manifolds (resp. knots) are bordism (resp. concordance) invariants.
The proof of the next lemma can be found in [Reference Letsche32, Proposition 2.8] or [Reference Cochran, Orr and Teichner9, Theorem 4.4].
Lemma 3.6. Let
![]() $N_{1},\ldots ,N_{k}$
be closed connected oriented
$N_{1},\ldots ,N_{k}$
be closed connected oriented
![]() $3$
-manifolds. Let
$3$
-manifolds. Let
![]() $\beta _{i} \colon \pi _{1}(N_{i}) \to GL_d({\mathbb {F}}[t^{\pm 1}])$
be a unitary acyclic representation for
$\beta _{i} \colon \pi _{1}(N_{i}) \to GL_d({\mathbb {F}}[t^{\pm 1}])$
be a unitary acyclic representation for
![]() $i=1,\ldots , k$
. Assume that W is a
$i=1,\ldots , k$
. Assume that W is a
![]() $4$
-manifold such that
$4$
-manifold such that
![]() $\partial W = N_{1} \sqcup \ldots \sqcup N_{k}$
and the two following conditions are satisfied:
$\partial W = N_{1} \sqcup \ldots \sqcup N_{k}$
and the two following conditions are satisfied:
-
(a) for
 $i=1,\ldots , k, $
there exists a unitary representation
$i=1,\ldots , k, $
there exists a unitary representation
 $\gamma \colon \pi _{1}(W) \to GL_d({\mathbb {F}}[t^{\pm 1}])$
extending the representations
$\gamma \colon \pi _{1}(W) \to GL_d({\mathbb {F}}[t^{\pm 1}])$
extending the representations
 $\beta _{i}$
;
$\beta _{i}$
; -
(b) the following sequence is exact:
(3.1) $$ \begin{align} TH_{2}(W, \partial W; \mathbb{F}[t^{\pm 1}]_{\gamma}^{d}) \xrightarrow{\partial} H_{1}(\partial W;\mathbb{F}[t^{\pm 1}]_{\gamma}^{d}) \xrightarrow{\iota_{\ast}} H_{1}(W; \mathbb{F}[t^{\pm 1}]_{\gamma}^{d}). \end{align} $$
$$ \begin{align} TH_{2}(W, \partial W; \mathbb{F}[t^{\pm 1}]_{\gamma}^{d}) \xrightarrow{\partial} H_{1}(\partial W;\mathbb{F}[t^{\pm 1}]_{\gamma}^{d}) \xrightarrow{\iota_{\ast}} H_{1}(W; \mathbb{F}[t^{\pm 1}]_{\gamma}^{d}). \end{align} $$
Then the linking form
![]() $\oplus _{i=1}^{k} \operatorname {\mathrm {Bl}}_{\beta _{i}}(N_{i})$
is metabolic.
$\oplus _{i=1}^{k} \operatorname {\mathrm {Bl}}_{\beta _{i}}(N_{i})$
is metabolic.
The following result uses Lemma 3.6 to provide (slightly less restrictive) assumptions under which the twisted Blanchfield pairing is metabolic.
Proposition 3.7. Let
![]() $N = N_{1} \sqcup \ldots \sqcup N_{k}$
be a disjoint union of closed
$N = N_{1} \sqcup \ldots \sqcup N_{k}$
be a disjoint union of closed
![]() $3$
-manifolds and let
$3$
-manifolds and let
![]() $\beta _{i} \colon \pi _{1}(N_{i}) \to ~GL_d({\mathbb {F}}[t^{\pm 1}])$
be a unitary acyclic representation for
$\beta _{i} \colon \pi _{1}(N_{i}) \to ~GL_d({\mathbb {F}}[t^{\pm 1}])$
be a unitary acyclic representation for
![]() $i=1,\ldots , k$
. If N bounds a compact
$i=1,\ldots , k$
. If N bounds a compact
![]() $4$
-manifold W and if the
$4$
-manifold W and if the
![]() $\beta _{i}$
extend to a unitary acyclic representation
$\beta _{i}$
extend to a unitary acyclic representation
![]() $\gamma \colon \pi _{1}(W) \to ~GL_d(\mathbb {F}[t^{\pm 1}])$
, then
$\gamma \colon \pi _{1}(W) \to ~GL_d(\mathbb {F}[t^{\pm 1}])$
, then
![]() $\oplus _{i=1}^{k}\operatorname {\mathrm {Bl}}_{\beta _{i}}(N_{i})$
is metabolic and, in particular, the sum
$\oplus _{i=1}^{k}\operatorname {\mathrm {Bl}}_{\beta _{i}}(N_{i})$
is metabolic and, in particular, the sum
![]() $\sum _{i=1}^{k}\sigma ^{\text {av}}_{N_i,\beta _{i}}$
of averaged signature functions is zero.
$\sum _{i=1}^{k}\sigma ^{\text {av}}_{N_i,\beta _{i}}$
of averaged signature functions is zero.
Proof. Since
![]() $\gamma $
is acyclic,
$\gamma $
is acyclic,
![]() $H_*(W;\mathbb {F}(t)_\gamma ^d)$
vanishes. Poincaré duality and the universal coefficient theorem (where the underlying ring is the PID
$H_*(W;\mathbb {F}(t)_\gamma ^d)$
vanishes. Poincaré duality and the universal coefficient theorem (where the underlying ring is the PID
![]() $R={\mathbb {F}}[t^{\pm 1}]$
) now imply that
$R={\mathbb {F}}[t^{\pm 1}]$
) now imply that
![]() $H_*(W,N;\mathbb {F}(t)_\gamma ^d)$
also vanishes. Since the
$H_*(W,N;\mathbb {F}(t)_\gamma ^d)$
also vanishes. Since the
![]() $\beta _i$
are acyclic, the homology
$\beta _i$
are acyclic, the homology
![]() $\mathbb {F}[t^{\pm 1}]$
-modules of
$\mathbb {F}[t^{\pm 1}]$
-modules of
![]() $N,W$
and
$N,W$
and
![]() $(W,N)$
are
$(W,N)$
are
![]() $\mathbb {F}[t^{\pm 1}]$
-torsion, and therefore, the sequence (3.1) is exact. The proposition now follows by applying Lemma 3.6 (to deduce that
$\mathbb {F}[t^{\pm 1}]$
-torsion, and therefore, the sequence (3.1) is exact. The proposition now follows by applying Lemma 3.6 (to deduce that
![]() $\oplus _{i=1}^{k}\operatorname {\mathrm {Bl}}_{\beta _{i}}(N_{i})$
is metabolic) and item (S-5) of Proposition 1.6 (to obtain that the sum of the signature functions is zero).
$\oplus _{i=1}^{k}\operatorname {\mathrm {Bl}}_{\beta _{i}}(N_{i})$
is metabolic) and item (S-5) of Proposition 1.6 (to obtain that the sum of the signature functions is zero).
Next, suppose that K and
![]() $K'$
are two concordant knots in
$K'$
are two concordant knots in
![]() $S^3$
and let
$S^3$
and let
![]() $M_K$
and
$M_K$
and
![]() $M_{K'}$
denote their respective
$M_{K'}$
denote their respective
![]() $0$
-framed surgeries. Given a locally flat concordance
$0$
-framed surgeries. Given a locally flat concordance
![]() $\Sigma \subset S^{3} \times I$
from K to
$\Sigma \subset S^{3} \times I$
from K to
![]() $K'$
, we can construct a cobordism
$K'$
, we can construct a cobordism
![]() $W_{\Sigma }$
from
$W_{\Sigma }$
from
![]() $M_{K}$
to
$M_{K}$
to
![]() $M_{K'}$
. Indeed, let
$M_{K'}$
. Indeed, let
![]() $\mathcal {N}(\Sigma )$
denote a tubular neighborhood of
$\mathcal {N}(\Sigma )$
denote a tubular neighborhood of
![]() $\Sigma $
(which can be identified with
$\Sigma $
(which can be identified with
![]() $\mathcal {N}(\Sigma ) \cong S^{1} \times D^{2} \times I$
).Footnote 3 The desired cobordism is then obtained by setting
$\mathcal {N}(\Sigma ) \cong S^{1} \times D^{2} \times I$
).Footnote 3 The desired cobordism is then obtained by setting
where
![]() $h \colon S^{1} \times S^{1} \times I \to S^{1} \times S^{1} \times I$
is the homeomorphism defined by
$h \colon S^{1} \times S^{1} \times I \to S^{1} \times S^{1} \times I$
is the homeomorphism defined by
![]() $h(x,y,z) = (y,x,z)$
. The next result shows that the averaged twisted signature is a concordance invariant as long as the corresponding representations extend through the complement of the concordance to an acyclic representation.
$h(x,y,z) = (y,x,z)$
. The next result shows that the averaged twisted signature is a concordance invariant as long as the corresponding representations extend through the complement of the concordance to an acyclic representation.
Proposition 3.8. Let
![]() $K_{1}, K_{2}$
be two concordant knots in
$K_{1}, K_{2}$
be two concordant knots in
![]() $S^3$
and let
$S^3$
and let
![]() $\beta _{i} \colon \pi _{1}(M_{K_{i}}) \to GL_d(\mathbb {F}[t^{\pm 1}])$
be a unitary acyclic representation for
$\beta _{i} \colon \pi _{1}(M_{K_{i}}) \to GL_d(\mathbb {F}[t^{\pm 1}])$
be a unitary acyclic representation for
![]() $i=1,2$
. Assume there is a concordance
$i=1,2$
. Assume there is a concordance
![]() $\Sigma \subset S^{3} \times I$
from
$\Sigma \subset S^{3} \times I$
from
![]() $K_{1}$
to
$K_{1}$
to
![]() $K_{2}$
and a unitary representation
$K_{2}$
and a unitary representation
![]() $\gamma \colon \pi _{1}(W_{\Sigma }) \to GL_d(\mathbb {F}[t^{\pm 1}])$
such that
$\gamma \colon \pi _{1}(W_{\Sigma }) \to GL_d(\mathbb {F}[t^{\pm 1}])$
such that
-
(a) the representations
 $\beta _{i}$
factor as
$\beta _{i}$
factor as
 $\gamma \circ (\iota _{i})_{\ast }$
, where
$\gamma \circ (\iota _{i})_{\ast }$
, where
 $\iota _{i} \colon M_{K_{i}} \hookrightarrow W_{\Sigma }$
is the inclusion for
$\iota _{i} \colon M_{K_{i}} \hookrightarrow W_{\Sigma }$
is the inclusion for
 $i=1,2$
;
$i=1,2$
; -
(b) the representation
 $\gamma $
is acyclic.
$\gamma $
is acyclic.
Then the twisted Blanchfield pairings
![]() $\operatorname {\mathrm {Bl}}_{\beta _{1}}(K_1)$
and
$\operatorname {\mathrm {Bl}}_{\beta _{1}}(K_1)$
and
![]() $\operatorname {\mathrm {Bl}}_{\beta _{2}}(K_2)$
are Witt equivalent and, in particular, the averaged signature functions
$\operatorname {\mathrm {Bl}}_{\beta _{2}}(K_2)$
are Witt equivalent and, in particular, the averaged signature functions
![]() $\sigma ^{av}_{K_{1},\beta _{1}}$
and
$\sigma ^{av}_{K_{1},\beta _{1}}$
and
![]() $\sigma ^{av}_{K_{2},\beta _{2}}$
agree.
$\sigma ^{av}_{K_{2},\beta _{2}}$
agree.
Proof. Set
![]() $N = M_{K_{1}} \sqcup -M_{K_{2}}$
. By our assumptions,
$N = M_{K_{1}} \sqcup -M_{K_{2}}$
. By our assumptions,
![]() $W_{\Sigma }$
is a null-bordism for N and satisfies the conditions of Proposition 3.7. Therefore,
$W_{\Sigma }$
is a null-bordism for N and satisfies the conditions of Proposition 3.7. Therefore,
![]() $\operatorname {\mathrm {Bl}}_{\beta _{1}}(M_{K_{1}}) \oplus \operatorname {\mathrm {Bl}}_{\beta _{2}}(-M_{K_{2}})$
is metabolic. Since
$\operatorname {\mathrm {Bl}}_{\beta _{1}}(M_{K_{1}}) \oplus \operatorname {\mathrm {Bl}}_{\beta _{2}}(-M_{K_{2}})$
is metabolic. Since
![]() $\operatorname {\mathrm {Bl}}_{\beta _{2}}(-M_{K_{2}}) = -\operatorname {\mathrm {Bl}}_{\beta _{2}}(M_{K_{2}})$
(use the same reasoning as in the proof of Proposition 3.4), it follows that
$\operatorname {\mathrm {Bl}}_{\beta _{2}}(-M_{K_{2}}) = -\operatorname {\mathrm {Bl}}_{\beta _{2}}(M_{K_{2}})$
(use the same reasoning as in the proof of Proposition 3.4), it follows that
![]() $\operatorname {\mathrm {Bl}}_{\beta _{1}}(K_1)$
and
$\operatorname {\mathrm {Bl}}_{\beta _{1}}(K_1)$
and
![]() $\operatorname {\mathrm {Bl}}_{\beta _{2}}(K_2)$
are Witt equivalent, and consequently, the averaged signature functions agree:
$\operatorname {\mathrm {Bl}}_{\beta _{2}}(K_2)$
are Witt equivalent, and consequently, the averaged signature functions agree:
![]() $\sigma ^{\operatorname {av}}_{K_{1},\beta _{1}}=\sigma ^{\operatorname {av}}_{K_{2},\beta _{2}}$
.
$\sigma ^{\operatorname {av}}_{K_{1},\beta _{1}}=\sigma ^{\operatorname {av}}_{K_{2},\beta _{2}}$
.
The same proof yields a result for slice knots with a representation which extends to an acylic representation over the slice disk exterior. We record this result for completeness, as it was mentioned in the second item of Theorem 1.1 from the introduction.
Proposition 3.9. Let K be a slice knot and let
![]() $\beta \colon \pi _{1}(M_K) \to GL_d(\mathbb {F}[t^{\pm 1}])$
be a unitary acyclic representation. If
$\beta \colon \pi _{1}(M_K) \to GL_d(\mathbb {F}[t^{\pm 1}])$
be a unitary acyclic representation. If
![]() $D\subset D^4 $
is a slice disk for K and there is a unitary acyclic representation
$D\subset D^4 $
is a slice disk for K and there is a unitary acyclic representation
![]() $\gamma \colon \pi _{1}(D^4 \setminus \mathcal {N}(D)) \to GL_d(\mathbb {F}[t^{\pm 1}])$
extending
$\gamma \colon \pi _{1}(D^4 \setminus \mathcal {N}(D)) \to GL_d(\mathbb {F}[t^{\pm 1}])$
extending
![]() $\beta $
, then the twisted Blanchfield pairings
$\beta $
, then the twisted Blanchfield pairings
![]() $\operatorname {\mathrm {Bl}}_{\beta }(K)$
is metabolic and, in particular, the averaged signature function
$\operatorname {\mathrm {Bl}}_{\beta }(K)$
is metabolic and, in particular, the averaged signature function
![]() $\sigma ^{av}_{K,\beta }$
is zero.
$\sigma ^{av}_{K,\beta }$
is zero.
3.3 Satellite formulas for twisted signatures
In this subsection, we use a result of Friedl-Leidy-Nagel-Powell [Reference Friedl, Leidy, Nagel and Powell21] to understand the behavior of the twisted Blanchfield pairings and signatures under various satellite operations. In particular, these results provide twisted generalizations of well-known theorems for the classical Blanchfield pairing and Levine-Tristram signature.
Let Y be a
![]() $3$
-manifold with empty or toroidal boundary. Suppose that we are given a simple closed curve
$3$
-manifold with empty or toroidal boundary. Suppose that we are given a simple closed curve
![]() $\eta $
in Y. If
$\eta $
in Y. If
![]() $K \subset S^{3}$
is a knot, then an infection of Y by K is a
$K \subset S^{3}$
is a knot, then an infection of Y by K is a
![]() $3$
-manifold
$3$
-manifold
![]() $Y_{K}$
obtained by gluing
$Y_{K}$
obtained by gluing
![]() $Y_{K} = (Y \setminus \mathcal {N}(\eta )) \cup _{\partial } S^{3} \setminus \mathcal {N}(K)$
, where we glue a zero-framed longitude of K to the meridian of
$Y_{K} = (Y \setminus \mathcal {N}(\eta )) \cup _{\partial } S^{3} \setminus \mathcal {N}(K)$
, where we glue a zero-framed longitude of K to the meridian of
![]() $\eta $
and some longitude of
$\eta $
and some longitude of
![]() $\eta $
to the meridian of K. Notice that the ambiguity in the choice of the longitude of
$\eta $
to the meridian of K. Notice that the ambiguity in the choice of the longitude of
![]() $\eta $
may lead to different outcomes; however, as pointed out in [Reference Friedl, Leidy, Nagel and Powell21], the resulting twisted Blanchfield pairing does not depend on this choice. Note that if Y has a boundary, then so does
$\eta $
may lead to different outcomes; however, as pointed out in [Reference Friedl, Leidy, Nagel and Powell21], the resulting twisted Blanchfield pairing does not depend on this choice. Note that if Y has a boundary, then so does
![]() $Y_K$
. In this case, we use Remark 2.3 which describes twisted Blanchfield pairings for
$Y_K$
. In this case, we use Remark 2.3 which describes twisted Blanchfield pairings for
![]() $3$
-manifolds with boundary.
$3$
-manifolds with boundary.
Let
![]() $P \subset S^{3}$
be a knot and let
$P \subset S^{3}$
be a knot and let
![]() $M_{P}$
be the zero-surgery on P. If
$M_{P}$
be the zero-surgery on P. If
![]() $K \subset S^{3}$
is another knot and
$K \subset S^{3}$
is another knot and
![]() $\eta $
is a simple closed curve in the complement of P, we can form the satellite knot
$\eta $
is a simple closed curve in the complement of P, we can form the satellite knot
![]() $P(K,\eta )$
with pattern P, companion C and infection curve
$P(K,\eta )$
with pattern P, companion C and infection curve
![]() $\eta $
by looking at the image of P under the diffeomorphism
$\eta $
by looking at the image of P under the diffeomorphism
![]() $(S^{3}\setminus \mathcal {N}(\eta )) \cup _{\partial } (S^{3} \setminus \mathcal {N}(K)) \cong S^{3}$
, where the gluing of the exteriors of
$(S^{3}\setminus \mathcal {N}(\eta )) \cup _{\partial } (S^{3} \setminus \mathcal {N}(K)) \cong S^{3}$
, where the gluing of the exteriors of
![]() $\eta $
and K identifies the meridian of
$\eta $
and K identifies the meridian of
![]() $\eta $
with the zero-framed longitude of K and vice versa.
$\eta $
with the zero-framed longitude of K and vice versa.
From this description, one can see that the zero-surgery on the satellite knot
![]() $P(K,\eta )$
can be obtained by infection of
$P(K,\eta )$
can be obtained by infection of
![]() $M_{P}$
by K along
$M_{P}$
by K along
![]() $\eta \subset S^{3} \setminus P \subset M_{P}$
:
$\eta \subset S^{3} \setminus P \subset M_{P}$
:
Let
![]() $\mu _{\eta }$
denote a meridian of
$\mu _{\eta }$
denote a meridian of
![]() $\eta $
. Our goal in this section is to express the Blanchfield form
$\eta $
. Our goal in this section is to express the Blanchfield form
![]() $\operatorname {\mathrm {Bl}}_\gamma (M_{P(K,\eta )})$
in terms of the twisted Blanchfield forms on
$\operatorname {\mathrm {Bl}}_\gamma (M_{P(K,\eta )})$
in terms of the twisted Blanchfield forms on
![]() $M_{P}$
and
$M_{P}$
and
![]() $M_{K}$
. Using (3.2), notice that given a representation
$M_{K}$
. Using (3.2), notice that given a representation
![]() $\gamma \colon \pi _{1}(M_{P(K,\eta )}) \to GL_d(\mathbb {F}[t^{\pm 1}])$
, there are induced representations
$\gamma \colon \pi _{1}(M_{P(K,\eta )}) \to GL_d(\mathbb {F}[t^{\pm 1}])$
, there are induced representations
In general, however, there is no guarantee that these representations can be extended to representations of the fundamental groups of
![]() $M_{P}$
and
$M_{P}$
and
![]() $M_{K}$
.
$M_{K}$
.
Remark 3.10. In fact,
![]() $\gamma _{P}$
and
$\gamma _{P}$
and
![]() $\gamma _{K}$
extend to representations of the respective zero-surgeries if and only if
$\gamma _{K}$
extend to representations of the respective zero-surgeries if and only if
![]() $\gamma (\mu _{\eta }) = 1$
. This follows from the following two observations. First,
$\gamma (\mu _{\eta }) = 1$
. This follows from the following two observations. First,
![]() $\mu _{\eta }$
is identified with the zero-framed longitude of K. Second, by van Kampen’s theorem, the inclusion
$\mu _{\eta }$
is identified with the zero-framed longitude of K. Second, by van Kampen’s theorem, the inclusion
![]() $M_{P} \setminus \mathcal {N}(\eta ) \hookrightarrow M_{P}$
induces a surjection
$M_{P} \setminus \mathcal {N}(\eta ) \hookrightarrow M_{P}$
induces a surjection
![]() $\pi _{1}(M_{P} \setminus \mathcal {N}(\eta )) \twoheadrightarrow \pi _{1}(M_{P})$
with kernel normally generated by
$\pi _{1}(M_{P} \setminus \mathcal {N}(\eta )) \twoheadrightarrow \pi _{1}(M_{P})$
with kernel normally generated by
![]() $\mu _{\eta }$
.
$\mu _{\eta }$
.
We say that a representation
![]() $\gamma \colon \pi _{1}(M_{P(K,\eta )}) \to GL_d(\mathbb {F}[t^{\pm 1}])$
is
$\gamma \colon \pi _{1}(M_{P(K,\eta )}) \to GL_d(\mathbb {F}[t^{\pm 1}])$
is
![]() $\eta $
-regular if
$\eta $
-regular if
![]() $\gamma (\mu _{\eta }) = \operatorname {id}$
and
$\gamma (\mu _{\eta }) = \operatorname {id}$
and
![]() $\det (\operatorname {id} - \gamma (\eta )) \neq 0$
. As explained in Remark 3.10, if
$\det (\operatorname {id} - \gamma (\eta )) \neq 0$
. As explained in Remark 3.10, if
![]() $\gamma $
is
$\gamma $
is
![]() $\eta $
-regular, then it induces well-defined representations
$\eta $
-regular, then it induces well-defined representations
![]() $\gamma _P$
and
$\gamma _P$
and
![]() $\gamma _K$
on
$\gamma _K$
on
![]() $\pi _1(M_P)$
and
$\pi _1(M_P)$
and
![]() $\pi _1(M_K)$
.
$\pi _1(M_K)$
.
Before proceeding to the next theorem, it is necessary to recall some terminology from [Reference Borodzik, Conway and Politarczyk3, Section 4.1]. If
![]() $(M,\lambda )$
is a linking form, then, for any submodule
$(M,\lambda )$
is a linking form, then, for any submodule
![]() $L \subset M$
, the orthogonal complement of L is defined as
$L \subset M$
, the orthogonal complement of L is defined as
![]() $L^{\perp } = \{x \in M \mid \ \lambda (x,y) = 0 \ \forall {y \in L} \}$
. We say that L is a sublagrangian (or isotropic) submodule if
$L^{\perp } = \{x \in M \mid \ \lambda (x,y) = 0 \ \forall {y \in L} \}$
. We say that L is a sublagrangian (or isotropic) submodule if
![]() $L \subset L^{\perp }$
. For a sublagrangian submodule
$L \subset L^{\perp }$
. For a sublagrangian submodule
![]() $L \subset M$
, the sublagrangian reduction of
$L \subset M$
, the sublagrangian reduction of
![]() $M $
by
$M $
by
![]() $ L $
is defined as
$ L $
is defined as
![]() $(L^{\perp }/L, \lambda _{L})$
, where
$(L^{\perp }/L, \lambda _{L})$
, where
![]() $\lambda _{L}(x+L,y+L) := \lambda (x,y)$
. Note that
$\lambda _{L}(x+L,y+L) := \lambda (x,y)$
. Note that
![]() $\lambda $
and
$\lambda $
and
![]() $\lambda _L$
are Witt equivalent, and therefore, by Proposition 1.6, the averaged signature functions of
$\lambda _L$
are Witt equivalent, and therefore, by Proposition 1.6, the averaged signature functions of
![]() $(M,\lambda )$
and its sublagrangian reduction are equal. The following theorem describes the twisted Blanchfield pairing of satellite knots and proves Theorem 1.5 from the introduction.
$(M,\lambda )$
and its sublagrangian reduction are equal. The following theorem describes the twisted Blanchfield pairing of satellite knots and proves Theorem 1.5 from the introduction.
Theorem 3.11. Let
![]() $K,P$
be knots and let
$K,P$
be knots and let
![]() $\eta $
be a simple closed curve in
$\eta $
be a simple closed curve in
![]() $S^3 \setminus P \subset M_P$
. Let
$S^3 \setminus P \subset M_P$
. Let
![]() $\gamma \colon \pi _{1}(M_{P(K,\eta )}) \to GL_d(\mathbb {F}[t^{\pm 1}])$
be a unitary acyclic
$\gamma \colon \pi _{1}(M_{P(K,\eta )}) \to GL_d(\mathbb {F}[t^{\pm 1}])$
be a unitary acyclic
![]() $\eta $
-regular representation. Let
$\eta $
-regular representation. Let
![]() $T \subset M_{P(K,\eta )}$
denote the common boundary of
$T \subset M_{P(K,\eta )}$
denote the common boundary of
![]() $M_{P}\setminus \mathcal {N}(\eta )$
and
$M_{P}\setminus \mathcal {N}(\eta )$
and
![]() $S^{3} \setminus \mathcal {N}(K)$
. Define
$S^{3} \setminus \mathcal {N}(K)$
. Define
The following assertions hold:
-
(1) The representations
 $\gamma _P$
and
$\gamma _P$
and
 $\gamma _K$
are unitary and acyclic.
$\gamma _K$
are unitary and acyclic. -
(2) The module L is isotropic and
 $\operatorname {\mathrm {ord}} L$
divides
$\operatorname {\mathrm {ord}} L$
divides
 $\det (1-\gamma (\eta ))$
.
$\det (1-\gamma (\eta ))$
. -
(3) The sublagrangian reduction of
 $\operatorname {\mathrm {Bl}}_\gamma (P(K,\eta ))$
with respect to L is isometric to the direct sum
$\operatorname {\mathrm {Bl}}_\gamma (P(K,\eta ))$
with respect to L is isometric to the direct sum
 $\operatorname {\mathrm {Bl}}_{\gamma _{P}}(P) \oplus \operatorname {\mathrm {Bl}}_{\gamma _K}(K)$
. In particular,
$\operatorname {\mathrm {Bl}}_{\gamma _{P}}(P) \oplus \operatorname {\mathrm {Bl}}_{\gamma _K}(K)$
. In particular,
 $\operatorname {\mathrm {Bl}}_\gamma (P(K,\eta ))$
is Witt equivalent to
$\operatorname {\mathrm {Bl}}_\gamma (P(K,\eta ))$
is Witt equivalent to
 $\operatorname {\mathrm {Bl}}_{\gamma _{P}}(P) \oplus \operatorname {\mathrm {Bl}}_{\gamma _K}(K)$
.
$\operatorname {\mathrm {Bl}}_{\gamma _{P}}(P) \oplus \operatorname {\mathrm {Bl}}_{\gamma _K}(K)$
.
The proof relies on the following result from [Reference Borodzik, Conway and Politarczyk3, Theorem 4.13] whose statement we recall for the reader’s convenience.
Theorem 3.12. Let
![]() $(M',\lambda ')$
and
$(M',\lambda ')$
and
![]() $(M",\lambda ")$
be two non-singular linking forms over
$(M",\lambda ")$
be two non-singular linking forms over
![]() ${\mathbb {F}}[t^{\pm 1}]$
, let M be a
${\mathbb {F}}[t^{\pm 1}]$
, let M be a
![]() ${\mathbb {F}}[t^{\pm 1}]$
-module and let
${\mathbb {F}}[t^{\pm 1}]$
-module and let
![]() $\iota \colon M\to M'$
be a monomorphism. Write
$\iota \colon M\to M'$
be a monomorphism. Write
![]() $\lambda $
for the form on M induced by
$\lambda $
for the form on M induced by
![]() $\iota $
. Suppose that
$\iota $
. Suppose that
![]() $\pi \colon (M,\lambda )\to (M",\lambda ")$
is a surjective morphism of linking forms and set
$\pi \colon (M,\lambda )\to (M",\lambda ")$
is a surjective morphism of linking forms and set
![]() $L:=\ker (\pi )$
and
$L:=\ker (\pi )$
and
![]() $L':=\iota (L)$
. Then
$L':=\iota (L)$
. Then
![]() $\operatorname {\mathrm {ord}}(M)\operatorname {\mathrm {ord}}(M)^\#$
divides
$\operatorname {\mathrm {ord}}(M)\operatorname {\mathrm {ord}}(M)^\#$
divides
![]() $\operatorname {\mathrm {ord}}(M')\operatorname {\mathrm {ord}}(M")$
. Moreover, if
$\operatorname {\mathrm {ord}}(M')\operatorname {\mathrm {ord}}(M")$
. Moreover, if
then the following statements hold:
-
(1)
 $\iota (M)={L'}^{\perp }$
;
$\iota (M)={L'}^{\perp }$
; -
(2) The linking form
 $(M",\lambda ")$
is isometric to the sublagrangian reduction of
$(M",\lambda ")$
is isometric to the sublagrangian reduction of
 $M'$
with respect to
$M'$
with respect to
 $L'$
. In particular,
$L'$
. In particular,
 $(M',\lambda ')$
and
$(M',\lambda ')$
and
 $(M",\lambda ")$
are Witt equivalent.
$(M",\lambda ")$
are Witt equivalent.
Proof of Theorem 3.11
During this proof, in order to simplify the notation, we will omit coefficients. As we mentioned in the statement, the torus T can be described either as
![]() $\partial (M_{P} \setminus \mathcal {N}(\eta ))$
or as
$\partial (M_{P} \setminus \mathcal {N}(\eta ))$
or as
![]() $ \partial (S^{3} \setminus \mathcal {N}(K))$
. As a consequence, we have
$ \partial (S^{3} \setminus \mathcal {N}(K))$
. As a consequence, we have
![]() $M_{P(K,\eta )} = (M_{P} \setminus \mathcal {N}(\eta ))\cup _{ T}(S^{3} \setminus \mathcal {N}(K))$
. Applying [Reference Friedl, Leidy, Nagel and Powell21, Theorem 1.1], we know that if
$M_{P(K,\eta )} = (M_{P} \setminus \mathcal {N}(\eta ))\cup _{ T}(S^{3} \setminus \mathcal {N}(K))$
. Applying [Reference Friedl, Leidy, Nagel and Powell21, Theorem 1.1], we know that if
![]() $H_*(T)$
and
$H_*(T)$
and
![]() $H_*(M_{P(K,\eta )})$
are
$H_*(M_{P(K,\eta )})$
are
![]() ${\mathbb {F}}[t^{\pm 1}]$
-torsion modules, then
${\mathbb {F}}[t^{\pm 1}]$
-torsion modules, then
![]() $H_*(M_{P} \setminus \mathcal {N}(\eta ))$
and
$H_*(M_{P} \setminus \mathcal {N}(\eta ))$
and
![]() $H_*(S^{3} \setminus \mathcal {N}(K))$
are also
$H_*(S^{3} \setminus \mathcal {N}(K))$
are also
![]() ${\mathbb {F}}[t^{\pm 1}]$
-torsion modules, and the direct sum of the canonical inclusions induces the following morphism of linking forms:
${\mathbb {F}}[t^{\pm 1}]$
-torsion modules, and the direct sum of the canonical inclusions induces the following morphism of linking forms:
Note that although [Reference Friedl, Leidy, Nagel and Powell21, Theorem 1.1] is stated for Ore domain coefficients, Proposition 2.8 implies that it also holds in the twisted setting. The next paragraph is devoted to checking that
![]() $H_*(M_{P(K,\eta )})$
and
$H_*(M_{P(K,\eta )})$
and
![]() $H_*(T)$
are indeed
$H_*(T)$
are indeed
![]() ${\mathbb {F}}[t^{\pm 1}]$
-torsion modules. Since the representation
${\mathbb {F}}[t^{\pm 1}]$
-torsion modules. Since the representation
![]() $\gamma $
was assumed to be acyclic,
$\gamma $
was assumed to be acyclic,
![]() $H_*(M_{P(K,\eta )})$
is indeed torsion. We must only show that
$H_*(M_{P(K,\eta )})$
is indeed torsion. We must only show that
![]() $H_*(T)$
is torsion. We assert that
$H_*(T)$
is torsion. We assert that
 $$ \begin{align} H_{i}(T) = \begin{cases} \mathbb{F}[t^{\pm1}]^{d} / (1-\gamma(\eta)) & i = 0,1, \\ 0 & \text{otherwise}. \end{cases} \end{align} $$
$$ \begin{align} H_{i}(T) = \begin{cases} \mathbb{F}[t^{\pm1}]^{d} / (1-\gamma(\eta)) & i = 0,1, \\ 0 & \text{otherwise}. \end{cases} \end{align} $$
Indeed, arguing as in [Reference Powell41, Proposition 3.11], we see that the twisted chain complex
![]() $C_{\ast }(T)$
is chain homotopy equivalent to
$C_{\ast }(T)$
is chain homotopy equivalent to
with a basis of
![]() $C_{1}(T) \cong \mathbb {F}[t^{\pm 1}]^{2d} $
given by the
$C_{1}(T) \cong \mathbb {F}[t^{\pm 1}]^{2d} $
given by the
![]() $\mu _{\eta } \otimes e_i $
and
$\mu _{\eta } \otimes e_i $
and
![]() $\eta \otimes e_i$
for
$\eta \otimes e_i$
for
![]() $i=1,\ldots ,d$
. Since
$i=1,\ldots ,d$
. Since
![]() $\gamma $
is
$\gamma $
is
![]() $\eta $
-regular,
$\eta $
-regular,
![]() $\gamma (\mu _{\eta })=1$
and the assertion follows. For later use, note that this argument also proves that the
$\gamma (\mu _{\eta })=1$
and the assertion follows. For later use, note that this argument also proves that the
![]() $\mathbb {F}[t^{\pm 1}]$
-module
$\mathbb {F}[t^{\pm 1}]$
-module
![]() $H_{1}(T)$
is generated by the homology classes
$H_{1}(T)$
is generated by the homology classes
![]() $[e_i \otimes \mu _{\eta }]$
for
$[e_i \otimes \mu _{\eta }]$
for
![]() $i=1,\ldots ,d$
. Since
$i=1,\ldots ,d$
. Since
![]() $\gamma $
is
$\gamma $
is
![]() $\eta $
-regular, (3.5) shows that
$\eta $
-regular, (3.5) shows that
![]() $H_*(T)$
is torsion, concluding our verification of the assumptions of [Reference Friedl, Leidy, Nagel and Powell21, Theorem 1.1] and thus establishing the existence of the morphism
$H_*(T)$
is torsion, concluding our verification of the assumptions of [Reference Friedl, Leidy, Nagel and Powell21, Theorem 1.1] and thus establishing the existence of the morphism
![]() $\psi $
in (3.4).
$\psi $
in (3.4).
Our goal is now to relate the Blanchfield pairings on
![]() $M_P,M_K$
and
$M_P,M_K$
and
![]() $M_{P(K,\eta )}$
. Observe that the
$M_{P(K,\eta )}$
. Observe that the
![]() ${\mathbb {F}}[t^{\pm 1}]$
-modules
${\mathbb {F}}[t^{\pm 1}]$
-modules
![]() $H_1(M_{P(K,\eta )}), H_1(M_{P} \setminus \mathcal {N}(\eta ),T)$
and
$H_1(M_{P(K,\eta )}), H_1(M_{P} \setminus \mathcal {N}(\eta ),T)$
and
![]() $H_1(S^{3} \setminus \mathcal {N}(K),T)$
are torsion: for
$H_1(S^{3} \setminus \mathcal {N}(K),T)$
are torsion: for
![]() $H_1(M_{P(K,\eta )})$
, this follows from the
$H_1(M_{P(K,\eta )})$
, this follows from the
![]() $\eta $
-regularity of
$\eta $
-regularity of
![]() $\gamma $
. For the two latter modules, this can be seen by looking at the long exact sequence of the pairs
$\gamma $
. For the two latter modules, this can be seen by looking at the long exact sequence of the pairs
![]() $(S^{3} \setminus \mathcal {N}(K),T)$
and
$(S^{3} \setminus \mathcal {N}(K),T)$
and
![]() $(M_{P} \setminus \mathcal {N}(\eta ),T)$
together with the fact that
$(M_{P} \setminus \mathcal {N}(\eta ),T)$
together with the fact that
![]() $H_1(M_{P} \setminus \mathcal {N}(\eta )),H_1(S^{3} \setminus \mathcal {N}(K))$
and
$H_1(M_{P} \setminus \mathcal {N}(\eta )),H_1(S^{3} \setminus \mathcal {N}(K))$
and
![]() $H_*(T)$
are all
$H_*(T)$
are all
![]() ${\mathbb {F}}[t^{\pm 1}]$
-torsion.
${\mathbb {F}}[t^{\pm 1}]$
-torsion.
Combining this observation with
![]() $ H_{0}(M_{P} \setminus \mathcal {N}(\eta ),T) = 0=H_{0}(M_{P} \setminus \mathcal {N}(\eta ),T)$
, Poincaré duality and the universal coefficient theorem (where the underlying ring is the PID
$ H_{0}(M_{P} \setminus \mathcal {N}(\eta ),T) = 0=H_{0}(M_{P} \setminus \mathcal {N}(\eta ),T)$
, Poincaré duality and the universal coefficient theorem (where the underlying ring is the PID
![]() ${\mathbb {F}}[t^{\pm 1}]$
), we obtain the following isomorphisms:
${\mathbb {F}}[t^{\pm 1}]$
), we obtain the following isomorphisms:
In more details, in each of the three lines, in our application of the universal coefficient theorem, we used our observation that the relevant first homology modules are
![]() ${\mathbb {F}}[t^{\pm 1}]$
-torsion. In the third isomorphism of (3.6), we also used the fact that for any torsion
${\mathbb {F}}[t^{\pm 1}]$
-torsion. In the third isomorphism of (3.6), we also used the fact that for any torsion
![]() ${\mathbb {F}}[t^{\pm 1}]$
-module T, we have
${\mathbb {F}}[t^{\pm 1}]$
-module T, we have
![]() $\operatorname {Ext}^{1}_{{\mathbb {F}}[t^{\pm 1}]}(T,{\mathbb {F}}[t^{\pm 1}]) \cong ~T$
.
$\operatorname {Ext}^{1}_{{\mathbb {F}}[t^{\pm 1}]}(T,{\mathbb {F}}[t^{\pm 1}]) \cong ~T$
.
Our strategy to relate the various Blanchfield pairings is to apply Theorem 3.12. We now introduce the notation necessary to its application as well as verify one of its key assumptions.
Lemma 3.13. The inclusions
![]() $\iota _{P} \colon M_{P} \setminus \mathcal {N}(\eta ) \hookrightarrow M_{P}$
and
$\iota _{P} \colon M_{P} \setminus \mathcal {N}(\eta ) \hookrightarrow M_{P}$
and
![]() $\iota _{K} \colon S^{3} \setminus \mathcal {N}(K) \hookrightarrow M_{K}$
induce isomorphisms on twisted homology in degree
$\iota _{K} \colon S^{3} \setminus \mathcal {N}(K) \hookrightarrow M_{K}$
induce isomorphisms on twisted homology in degree
![]() $j \neq 1,2$
and epimorphisms
$j \neq 1,2$
and epimorphisms
![]() $ (\iota _{P})_{\ast }, (\iota _{K})_{\ast }$
in degree one. Moreover,
$ (\iota _{P})_{\ast }, (\iota _{K})_{\ast }$
in degree one. Moreover,
![]() $\ker (\iota _{P})_{\ast }$
and
$\ker (\iota _{P})_{\ast }$
and
![]() $\ker (\iota _{K})_{\ast }$
are generated by the
$\ker (\iota _{K})_{\ast }$
are generated by the
![]() $[e_i \otimes \mu _{\eta }]$
for
$[e_i \otimes \mu _{\eta }]$
for
![]() $i=1,\ldots , d$
. Additionally, the modules
$i=1,\ldots , d$
. Additionally, the modules
![]() $H_1(M_K)$
and
$H_1(M_K)$
and
![]() $H_1(M_P)$
are
$H_1(M_P)$
are
![]() ${\mathbb {F}}[t^{\pm 1}]$
-torsion. Finally, we have the following equalities:
${\mathbb {F}}[t^{\pm 1}]$
-torsion. Finally, we have the following equalities:
 $$ \begin{align*} \operatorname{\mathrm{ord}} H_{1}(M_{P} \setminus \mathcal{N}(\eta)) &\doteq \frac{\operatorname{\mathrm{ord}}(H_{1}(M_{P})) \cdot \operatorname{\mathrm{ord}}(H_{1}(T))}{\operatorname{\mathrm{ord}}(H_{0}(M_{P}))^\#}, \\ \operatorname{\mathrm{ord}} H_{1}(S^{3} \setminus \mathcal{N}(K)) &\doteq \frac{\operatorname{\mathrm{ord}}(H_{1}(M_{K})) \cdot \operatorname{\mathrm{ord}}(H_{1}(T))}{\operatorname{\mathrm{ord}}(H_{0}(M_{K}))^\# }. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{ord}} H_{1}(M_{P} \setminus \mathcal{N}(\eta)) &\doteq \frac{\operatorname{\mathrm{ord}}(H_{1}(M_{P})) \cdot \operatorname{\mathrm{ord}}(H_{1}(T))}{\operatorname{\mathrm{ord}}(H_{0}(M_{P}))^\#}, \\ \operatorname{\mathrm{ord}} H_{1}(S^{3} \setminus \mathcal{N}(K)) &\doteq \frac{\operatorname{\mathrm{ord}}(H_{1}(M_{K})) \cdot \operatorname{\mathrm{ord}}(H_{1}(T))}{\operatorname{\mathrm{ord}}(H_{0}(M_{K}))^\# }. \end{align*} $$
Proof. We only prove the lemma for
![]() $M_{P} \setminus \mathcal {N}(\eta )$
: the proof for
$M_{P} \setminus \mathcal {N}(\eta )$
: the proof for
![]() $S^{3} \setminus \mathcal {N}(K)$
is completely analogous. Using (3.5) and the Mayer-Vietoris sequence of
$S^{3} \setminus \mathcal {N}(K)$
is completely analogous. Using (3.5) and the Mayer-Vietoris sequence of
![]() $M_{P} = (M_{P} \setminus \mathcal {N}(\eta )) \cup _T \mathcal {N}(\eta )$
, we deduce that
$M_{P} = (M_{P} \setminus \mathcal {N}(\eta )) \cup _T \mathcal {N}(\eta )$
, we deduce that
![]() $i_P$
does indeed induce an isomorphism on twisted homology in degree
$i_P$
does indeed induce an isomorphism on twisted homology in degree
![]() $j> 2$
. In degree zero, notice that the inclusion
$j> 2$
. In degree zero, notice that the inclusion
![]() $T \hookrightarrow \mathcal {N}(\eta )$
induces an isomorphism on
$T \hookrightarrow \mathcal {N}(\eta )$
induces an isomorphism on
![]() $H_{0}$
, and therefore, with the aid of the Mayer-Vietoris sequence, we obtain an isomorphism
$H_{0}$
, and therefore, with the aid of the Mayer-Vietoris sequence, we obtain an isomorphism
![]() $H_{0}(M_{P} \setminus \mathcal {N}(\eta )) \cong H_{0}(M_{P})$
.
$H_{0}(M_{P} \setminus \mathcal {N}(\eta )) \cong H_{0}(M_{P})$
.
To get the result in degrees
![]() $j=1,2$
, consider the relevant part of the Mayer-Vietoris sequence:
$j=1,2$
, consider the relevant part of the Mayer-Vietoris sequence:
Notice that the leftmost part of (3.9) is exact by (3.7). Since
![]() $H_1(M_P \setminus \mathcal {N}(\eta ))$
is
$H_1(M_P \setminus \mathcal {N}(\eta ))$
is
![]() ${\mathbb {F}}[t^{\pm 1}]$
-torsion, (3.9) implies that this is also the case for
${\mathbb {F}}[t^{\pm 1}]$
-torsion, (3.9) implies that this is also the case for
![]() $H_1(M_P)$
. Next, (3.9) also implies that the map
$H_1(M_P)$
. Next, (3.9) also implies that the map
![]() $(\iota _{P})_{\ast }$
is an epimorphism with kernel generated by the
$(\iota _{P})_{\ast }$
is an epimorphism with kernel generated by the
![]() $[e_i \otimes \mu _{\eta }]$
(or technically by
$[e_i \otimes \mu _{\eta }]$
(or technically by
![]() $ j_P([e_i \otimes \mu _{\eta }])$
, because
$ j_P([e_i \otimes \mu _{\eta }])$
, because
![]() $H_{1}(T)$
is generated by these elements. The last assertion of the lemma also follows from (3.9): we use the multiplicativity of the orders and the same isomorphisms as in (3.6) to establish the isomorphism
$H_{1}(T)$
is generated by these elements. The last assertion of the lemma also follows from (3.9): we use the multiplicativity of the orders and the same isomorphisms as in (3.6) to establish the isomorphism
![]() $H_{2}(M_{P}) \cong H_0(M_{P})^{\#}$
(this is possible since we now know that
$H_{2}(M_{P}) \cong H_0(M_{P})^{\#}$
(this is possible since we now know that
![]() $H_1(M_P)$
is torsion). This concludes the proof of the lemma.
$H_1(M_P)$
is torsion). This concludes the proof of the lemma.
We now prove the first assertion of the theorem – namely, that
![]() $\gamma _P$
and
$\gamma _P$
and
![]() $\gamma _K$
are acyclic. We only check this for
$\gamma _K$
are acyclic. We only check this for
![]() $\gamma _P$
: the proof for
$\gamma _P$
: the proof for
![]() $\gamma _K$
is identical. Since
$\gamma _K$
is identical. Since
![]() $H_*(M_P \setminus \mathcal {N}(\eta ))$
is
$H_*(M_P \setminus \mathcal {N}(\eta ))$
is
![]() ${\mathbb {F}}[t^{\pm 1}]$
-torsion, Lemma 3.13 implies that
${\mathbb {F}}[t^{\pm 1}]$
-torsion, Lemma 3.13 implies that
![]() $H_i(M_P)$
is
$H_i(M_P)$
is
![]() ${\mathbb {F}}[t^{\pm 1}]$
-torsion for
${\mathbb {F}}[t^{\pm 1}]$
-torsion for
![]() $i \neq 2$
. For
$i \neq 2$
. For
![]() $i=2$
, we use the isomorphism
$i=2$
, we use the isomorphism
![]() $H_2(M_P)\cong H_0(M_P)^\#$
(that we established in the proof of Lemma 3.13), and the conclusion follows. The first statement of Theorem 3.11 is now proved.
$H_2(M_P)\cong H_0(M_P)^\#$
(that we established in the proof of Lemma 3.13), and the conclusion follows. The first statement of Theorem 3.11 is now proved.
As a next step, consider the decomposition
![]() $M_{P(K,\eta )} = \left (M_{P}\setminus \mathcal {N}(\eta )\right ) \cup _T \left (S^{3} \setminus \mathcal {N}(K)\right )$
. The associated Mayer-Vietoris sequence can be decomposed into the following three exact sequences:
$M_{P(K,\eta )} = \left (M_{P}\setminus \mathcal {N}(\eta )\right ) \cup _T \left (S^{3} \setminus \mathcal {N}(K)\right )$
. The associated Mayer-Vietoris sequence can be decomposed into the following three exact sequences:
where
![]() $\mathcal {K}=\ker (\psi )$
and
$\mathcal {K}=\ker (\psi )$
and
![]() $\mathcal {C}=\operatorname {\mathrm {coker}}(\psi )$
. Therefore, applying the multiplicativity of the orders, the use of (3.10) and (3.12) (as well as (3.6)) implies that
$\mathcal {C}=\operatorname {\mathrm {coker}}(\psi )$
. Therefore, applying the multiplicativity of the orders, the use of (3.10) and (3.12) (as well as (3.6)) implies that
 $$ \begin{align*} \operatorname{\mathrm{ord}} (\mathcal{C}) &\doteq \frac{\operatorname{\mathrm{ord}}(H_{0}(T)) \cdot \operatorname{\mathrm{ord}}(H_{0}(M_{P(K,\eta)}))}{\operatorname{\mathrm{ord}}(H_{0}(M_{P}\setminus \mathcal{N}(\eta))) \cdot \operatorname{\mathrm{ord}}(H_{0}(S^{3} \setminus \mathcal{N}(K)))} \doteq \frac{\operatorname{\mathrm{ord}}(H_{0}(T)) \cdot \operatorname{\mathrm{ord}}(H_{0}(M_{P(K,\eta)}))}{\operatorname{\mathrm{ord}}(H_{0}(M_{P})) \cdot \operatorname{\mathrm{ord}}(H_{0}(M_{K}))}, \\ \operatorname{\mathrm{ord}} (\mathcal{K} )&\doteq \frac{\operatorname{\mathrm{ord}}(H_{1}(T))}{\operatorname{\mathrm{ord}}(H_{2}(M_{P(K,\eta)}))} \doteq \frac{\operatorname{\mathrm{ord}}(H_{1}(T))}{\operatorname{\mathrm{ord}}(H_{0}(M_{P(K,\eta)}))^\#}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{ord}} (\mathcal{C}) &\doteq \frac{\operatorname{\mathrm{ord}}(H_{0}(T)) \cdot \operatorname{\mathrm{ord}}(H_{0}(M_{P(K,\eta)}))}{\operatorname{\mathrm{ord}}(H_{0}(M_{P}\setminus \mathcal{N}(\eta))) \cdot \operatorname{\mathrm{ord}}(H_{0}(S^{3} \setminus \mathcal{N}(K)))} \doteq \frac{\operatorname{\mathrm{ord}}(H_{0}(T)) \cdot \operatorname{\mathrm{ord}}(H_{0}(M_{P(K,\eta)}))}{\operatorname{\mathrm{ord}}(H_{0}(M_{P})) \cdot \operatorname{\mathrm{ord}}(H_{0}(M_{K}))}, \\ \operatorname{\mathrm{ord}} (\mathcal{K} )&\doteq \frac{\operatorname{\mathrm{ord}}(H_{1}(T))}{\operatorname{\mathrm{ord}}(H_{2}(M_{P(K,\eta)}))} \doteq \frac{\operatorname{\mathrm{ord}}(H_{1}(T))}{\operatorname{\mathrm{ord}}(H_{0}(M_{P(K,\eta)}))^\#}. \end{align*} $$
The key
![]() ${\mathbb {F}}[t^{\pm 1}]$
-module required in this proof is defined as
${\mathbb {F}}[t^{\pm 1}]$
-module required in this proof is defined as
The module A will be used both in the proof of the second and third statements of Theorem 3.11. As a preliminary, however, we first compute
![]() $ \operatorname {\mathrm {ord}} (A) \operatorname {\mathrm {ord}} (A)^\# $
. Combining (3.11) with our computation of
$ \operatorname {\mathrm {ord}} (A) \operatorname {\mathrm {ord}} (A)^\# $
. Combining (3.11) with our computation of
![]() $\operatorname {\mathrm {ord}} (\mathcal {C})$
, we obtain
$\operatorname {\mathrm {ord}} (\mathcal {C})$
, we obtain
 $$\begin{align*}\operatorname{\mathrm{ord}} (A) \doteq \frac{\operatorname{\mathrm{ord}}(H_{1}(M_{P(K,\eta)}))}{\operatorname{\mathrm{ord}} (\mathcal{C})} \doteq \frac{\operatorname{\mathrm{ord}}(H_{1}(M_{P(K,\eta)})) \cdot \operatorname{\mathrm{ord}}(H_{0}(M_{P})) \cdot \operatorname{\mathrm{ord}} H_{0}(M_{K})}{\operatorname{\mathrm{ord}} (H_{0}(T)) \cdot \operatorname{\mathrm{ord}}(H_{0}(M_{P(K,\eta)}))}.\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{ord}} (A) \doteq \frac{\operatorname{\mathrm{ord}}(H_{1}(M_{P(K,\eta)}))}{\operatorname{\mathrm{ord}} (\mathcal{C})} \doteq \frac{\operatorname{\mathrm{ord}}(H_{1}(M_{P(K,\eta)})) \cdot \operatorname{\mathrm{ord}}(H_{0}(M_{P})) \cdot \operatorname{\mathrm{ord}} H_{0}(M_{K})}{\operatorname{\mathrm{ord}} (H_{0}(T)) \cdot \operatorname{\mathrm{ord}}(H_{0}(M_{P(K,\eta)}))}.\end{align*}$$
On the other hand, Lemma 3.13 and our computation of
![]() $\operatorname {\mathrm {ord}} (\mathcal {K})$
imply that
$\operatorname {\mathrm {ord}} (\mathcal {K})$
imply that
 $$ \begin{align*} \operatorname{\mathrm{ord}} (A) &\doteq \frac{\operatorname{\mathrm{ord}}(H_{1}(M_{P} \setminus \mathcal{N}(\eta))) \cdot \operatorname{\mathrm{ord}}(H_{1}(S^{3}\setminus \mathcal{N}(K)))}{\operatorname{\mathrm{ord}} (\mathcal{K})} \\ &\doteq \frac{\operatorname{\mathrm{ord}}(H_{1}(M_{P})) \cdot \operatorname{\mathrm{ord}}(H_{1}(M_{K})) \cdot \operatorname{\mathrm{ord}}(H_{1}(T))^{2} \cdot \operatorname{\mathrm{ord}}(H_{0}(M_{P(K,\eta)}))^\# }{\operatorname{\mathrm{ord}}(H_{0}(M_{P}))^\# \cdot \operatorname{\mathrm{ord}}(H_{0}(M_{K}))^\# \cdot \operatorname{\mathrm{ord}}(H_{1}(T))} \\ &\doteq \frac{\operatorname{\mathrm{ord}}(H_{1}(M_{P})) \cdot \operatorname{\mathrm{ord}}(H_{1}(M_{K})) \cdot \operatorname{\mathrm{ord}}(H_{1}(T)) \cdot \operatorname{\mathrm{ord}}(H_{0}(M_{P(K,\eta)}))^\# }{\operatorname{\mathrm{ord}}(H_{0}(M_{P}))^\# \cdot \operatorname{\mathrm{ord}}(H_{0}(M_{K}))^\# }. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{ord}} (A) &\doteq \frac{\operatorname{\mathrm{ord}}(H_{1}(M_{P} \setminus \mathcal{N}(\eta))) \cdot \operatorname{\mathrm{ord}}(H_{1}(S^{3}\setminus \mathcal{N}(K)))}{\operatorname{\mathrm{ord}} (\mathcal{K})} \\ &\doteq \frac{\operatorname{\mathrm{ord}}(H_{1}(M_{P})) \cdot \operatorname{\mathrm{ord}}(H_{1}(M_{K})) \cdot \operatorname{\mathrm{ord}}(H_{1}(T))^{2} \cdot \operatorname{\mathrm{ord}}(H_{0}(M_{P(K,\eta)}))^\# }{\operatorname{\mathrm{ord}}(H_{0}(M_{P}))^\# \cdot \operatorname{\mathrm{ord}}(H_{0}(M_{K}))^\# \cdot \operatorname{\mathrm{ord}}(H_{1}(T))} \\ &\doteq \frac{\operatorname{\mathrm{ord}}(H_{1}(M_{P})) \cdot \operatorname{\mathrm{ord}}(H_{1}(M_{K})) \cdot \operatorname{\mathrm{ord}}(H_{1}(T)) \cdot \operatorname{\mathrm{ord}}(H_{0}(M_{P(K,\eta)}))^\# }{\operatorname{\mathrm{ord}}(H_{0}(M_{P}))^\# \cdot \operatorname{\mathrm{ord}}(H_{0}(M_{K}))^\# }. \end{align*} $$
Additionally, observe that
![]() $\operatorname {\mathrm {ord}}(H_1(T))=\operatorname {\mathrm {ord}}(H_0(T))^\#$
(this follows by duality and the universal coefficient theorem) and
$\operatorname {\mathrm {ord}}(H_1(T))=\operatorname {\mathrm {ord}}(H_0(T))^\#$
(this follows by duality and the universal coefficient theorem) and
![]() $\operatorname {\mathrm {ord}}(H_1(M_{P(K,\eta )})=\operatorname {\mathrm {ord}}(H_1(M_{P(K,\eta )})^\#$
(since
$\operatorname {\mathrm {ord}}(H_1(M_{P(K,\eta )})=\operatorname {\mathrm {ord}}(H_1(M_{P(K,\eta )})^\#$
(since
![]() $H_1(M_{P(K,\eta )})$
supports a non-singular linking form). Combining these observations with the above formulas for
$H_1(M_{P(K,\eta )})$
supports a non-singular linking form). Combining these observations with the above formulas for
![]() $\operatorname {\mathrm {ord}} (A)$
, we obtain
$\operatorname {\mathrm {ord}} (A)$
, we obtain
We now prove the second statement of Theorem 3.11 which asserts that L is isotropic and that
![]() $\operatorname {\mathrm {ord}} (L)$
divides
$\operatorname {\mathrm {ord}} (L)$
divides
![]() $\det (1-\gamma (\eta ))$
. Observe that
$\det (1-\gamma (\eta ))$
. Observe that
![]() $(\iota _{P})_{\ast } \oplus (\iota _{K})_{\ast }$
and
$(\iota _{P})_{\ast } \oplus (\iota _{K})_{\ast }$
and
![]() $\psi $
vanish on
$\psi $
vanish on
![]() $\mathcal {K}$
. As a consequence, we let
$\mathcal {K}$
. As a consequence, we let
![]() $(\iota _{P})_{\ast } \oplus (\iota _{K})_{\ast } / \mathcal {K}$
and
$(\iota _{P})_{\ast } \oplus (\iota _{K})_{\ast } / \mathcal {K}$
and
![]() $\psi / \mathcal {K}$
denote the maps induced on A. Additionally, using
$\psi / \mathcal {K}$
denote the maps induced on A. Additionally, using
![]() $\widetilde {L}$
to denote the kernel of
$\widetilde {L}$
to denote the kernel of
![]() $(\iota _{P})_{\ast } \oplus (\iota _{K})_{\ast } / \mathcal {K}$
and
$(\iota _{P})_{\ast } \oplus (\iota _{K})_{\ast } / \mathcal {K}$
and
![]() $\operatorname {Cok}$
to denote the cokernel of
$\operatorname {Cok}$
to denote the cokernel of
![]() $\psi / \mathcal {K}$
, we obtain the following diagram of exact sequences:
$\psi / \mathcal {K}$
, we obtain the following diagram of exact sequences:

To check the second assertion of the theorem, we will show that
![]() $(\psi /\mathcal {K})(\widetilde {L}) = L$
, where L was defined as
$(\psi /\mathcal {K})(\widetilde {L}) = L$
, where L was defined as
![]() $\operatorname {im} (H_1(T) \to H_1(M_{P(K,\eta )}))$
. Use
$\operatorname {im} (H_1(T) \to H_1(M_{P(K,\eta )}))$
. Use
![]() $j_P$
(resp.
$j_P$
(resp.
![]() $j_K$
) to denote the map induced by the inclusion
$j_K$
) to denote the map induced by the inclusion
![]() $T \to M_P \setminus \mathcal {N}(\eta )$
(resp.
$T \to M_P \setminus \mathcal {N}(\eta )$
(resp.
![]() $T \to S^3 \setminus \mathcal {N}(K)$
). The exact sequence in (3.11) implies that
$T \to S^3 \setminus \mathcal {N}(K)$
). The exact sequence in (3.11) implies that
![]() $\mathcal {K}$
, treated as a submodule of
$\mathcal {K}$
, treated as a submodule of
![]() $H_{1}(M_{P}\setminus \mathcal {N}(\eta )) \oplus H_{1}(S^{3}\setminus \mathcal {N}(K))$
, is generated by
$H_{1}(M_{P}\setminus \mathcal {N}(\eta )) \oplus H_{1}(S^{3}\setminus \mathcal {N}(K))$
, is generated by
![]() $(j_{P}([e_{i} \otimes \mu _{\eta }]), -j_{K}([e_{i}\otimes \mu _{\eta }]))$
, for
$(j_{P}([e_{i} \otimes \mu _{\eta }]), -j_{K}([e_{i}\otimes \mu _{\eta }]))$
, for
![]() $i=1,\ldots , d$
. Therefore, for any i, we have
$i=1,\ldots , d$
. Therefore, for any i, we have
![]() $(j_{P}([e_{i} \otimes \mu _{\eta }]),0) = (0,j_{K}([e_{i} \otimes \mu _{\eta }]))$
in A. Moreover,
$(j_{P}([e_{i} \otimes \mu _{\eta }]),0) = (0,j_{K}([e_{i} \otimes \mu _{\eta }]))$
in A. Moreover,
and thus,
![]() $(\psi /\mathcal {K})(\widetilde {L}) = L$
. Since
$(\psi /\mathcal {K})(\widetilde {L}) = L$
. Since
![]() $\psi /\mathcal {K}$
is injective, it follows that L and
$\psi /\mathcal {K}$
is injective, it follows that L and
![]() $\widetilde {L}$
are isomorphic. In order to prove that L is isotropic, observe that the homology classes
$\widetilde {L}$
are isomorphic. In order to prove that L is isotropic, observe that the homology classes
![]() $[e_{i}\otimes \mu _{\eta }]$
belong to the radical of
$[e_{i}\otimes \mu _{\eta }]$
belong to the radical of
![]() $\operatorname {\mathrm {Bl}}_{\gamma _{P}}(M_{P} \setminus \mathcal {N}(\eta ))$
and
$\operatorname {\mathrm {Bl}}_{\gamma _{P}}(M_{P} \setminus \mathcal {N}(\eta ))$
and
![]() $\operatorname {\mathrm {Bl}}_{\gamma _{K}}(S^{3} \setminus \mathcal {N}(K))$
because they come from the boundary of the respective manifolds. Since
$\operatorname {\mathrm {Bl}}_{\gamma _{K}}(S^{3} \setminus \mathcal {N}(K))$
because they come from the boundary of the respective manifolds. Since
![]() $\psi $
and
$\psi $
and
![]() $\psi / \mathcal {K}$
are morphisms of linking forms, it follows that L is isotropic. The constraint on the order of L comes from the fact that L is a quotient of
$\psi / \mathcal {K}$
are morphisms of linking forms, it follows that L is isotropic. The constraint on the order of L comes from the fact that L is a quotient of
![]() $H_{1}(T)$
. This establishes the second statement of Theorem 3.11.
$H_{1}(T)$
. This establishes the second statement of Theorem 3.11.
We now move on to the third statement which describes the relation between
![]() $\operatorname {\mathrm {Bl}}_\gamma (P(K,\eta ))$
and
$\operatorname {\mathrm {Bl}}_\gamma (P(K,\eta ))$
and
![]() $\operatorname {\mathrm {Bl}}_{\gamma _P}(P) \oplus \operatorname {\mathrm {Bl}}_{\gamma _K}(K)$
. First observe that
$\operatorname {\mathrm {Bl}}_{\gamma _P}(P) \oplus \operatorname {\mathrm {Bl}}_{\gamma _K}(K)$
. First observe that
![]() $\operatorname {\mathrm {Bl}}_{\gamma _P}(M_P \setminus \mathcal {N}(\eta )) \oplus \operatorname {\mathrm {Bl}}_{\gamma _K}(S^3 \setminus \mathcal {N}(K)) $
vanishes on
$\operatorname {\mathrm {Bl}}_{\gamma _P}(M_P \setminus \mathcal {N}(\eta )) \oplus \operatorname {\mathrm {Bl}}_{\gamma _K}(S^3 \setminus \mathcal {N}(K)) $
vanishes on
![]() $\mathcal {K}$
: indeed,
$\mathcal {K}$
: indeed,
![]() $\mathcal {K}$
only contains homology classes which come from the boundary torus T. As a consequence,
$\mathcal {K}$
only contains homology classes which come from the boundary torus T. As a consequence,
![]() $\operatorname {\mathrm {Bl}}_{\gamma _P}(M_P \setminus \mathcal {N}(\eta )) \oplus \operatorname {\mathrm {Bl}}_{\gamma _K}(S^3 \setminus \mathcal {N}(K))$
descends to A.
$\operatorname {\mathrm {Bl}}_{\gamma _P}(M_P \setminus \mathcal {N}(\eta )) \oplus \operatorname {\mathrm {Bl}}_{\gamma _K}(S^3 \setminus \mathcal {N}(K))$
descends to A.
We wish to apply Theorem 3.12 to
![]() $(M",\lambda ")=\operatorname {\mathrm {Bl}}_\gamma (P(K,\eta )),(M',\lambda ')=\operatorname {\mathrm {Bl}}_{\gamma _P}(P) \oplus \operatorname {\mathrm {Bl}}_{\gamma _K}(K)$
with
$(M",\lambda ")=\operatorname {\mathrm {Bl}}_\gamma (P(K,\eta )),(M',\lambda ')=\operatorname {\mathrm {Bl}}_{\gamma _P}(P) \oplus \operatorname {\mathrm {Bl}}_{\gamma _K}(K)$
with
![]() $M=A,\iota =\psi /\mathcal {K}$
and
$M=A,\iota =\psi /\mathcal {K}$
and
![]() $\pi =(\iota _{P})_{\ast } \oplus (\iota _{K})_{\ast } / \mathcal {K}$
. First, it is clear that the maps
$\pi =(\iota _{P})_{\ast } \oplus (\iota _{K})_{\ast } / \mathcal {K}$
. First, it is clear that the maps
![]() $(\iota _{P})_{\ast } \oplus (\iota _{K})_{\ast } / \mathcal {K}$
and
$(\iota _{P})_{\ast } \oplus (\iota _{K})_{\ast } / \mathcal {K}$
and
![]() $\psi / \mathcal {K}$
are morphisms of linking forms. Next, by definition of
$\psi / \mathcal {K}$
are morphisms of linking forms. Next, by definition of
![]() $\mathcal {K}$
, the map
$\mathcal {K}$
, the map
![]() $\psi / \mathcal {K}$
is injective, while
$\psi / \mathcal {K}$
is injective, while
![]() $(\iota _{P})_{\ast } \oplus (\iota _{K})_{\ast } / \mathcal {K}$
is surjective thanks to (3.9). Since
$(\iota _{P})_{\ast } \oplus (\iota _{K})_{\ast } / \mathcal {K}$
is surjective thanks to (3.9). Since
![]() $M_P, M_K$
and
$M_P, M_K$
and
![]() $M_{P(K,\eta )}$
are closed manifolds, the corresponding Blanchfield forms are non-singular. Finally, we already showed in (3.13) that
$M_{P(K,\eta )}$
are closed manifolds, the corresponding Blanchfield forms are non-singular. Finally, we already showed in (3.13) that
![]() $\operatorname {\mathrm {ord}} (A) \cdot (\operatorname {\mathrm {ord}} (A))^\# \doteq \operatorname {\mathrm {ord}}(H_{1}(M_{P})) \cdot \operatorname {\mathrm {ord}}(H_{1}(M_{K})) \cdot \operatorname {\mathrm {ord}}(H_{1}(M_{P(K,\eta )}))$
. We can therefore apply Theorem 3.12 to the above diagram to obtain the third assertion of the theorem, concluding the proof.
$\operatorname {\mathrm {ord}} (A) \cdot (\operatorname {\mathrm {ord}} (A))^\# \doteq \operatorname {\mathrm {ord}}(H_{1}(M_{P})) \cdot \operatorname {\mathrm {ord}}(H_{1}(M_{K})) \cdot \operatorname {\mathrm {ord}}(H_{1}(M_{P(K,\eta )}))$
. We can therefore apply Theorem 3.12 to the above diagram to obtain the third assertion of the theorem, concluding the proof.
The next result shows that Blanchfield pairings need not be additive under satellite operations.
Corollary 3.14. Using the same assumptions as in Theorem 3.11, if
![]() $\operatorname {\mathrm {ord}} (L) $
is relatively prime to
$\operatorname {\mathrm {ord}} (L) $
is relatively prime to
![]() $\operatorname {\mathrm {ord}}(H_{1}(M_{P};{\mathbb {F}}[t^{\pm 1}]^{d}_{\gamma _{P}})) \cdot \operatorname {\mathrm {ord}}(H_{1}(M_{K};{\mathbb {F}}[t^{\pm 1}]^{d}_{\gamma _{K}}))$
, then there is an isometry of linking forms
$\operatorname {\mathrm {ord}}(H_{1}(M_{P};{\mathbb {F}}[t^{\pm 1}]^{d}_{\gamma _{P}})) \cdot \operatorname {\mathrm {ord}}(H_{1}(M_{K};{\mathbb {F}}[t^{\pm 1}]^{d}_{\gamma _{K}}))$
, then there is an isometry of linking forms
where
![]() $(X,\lambda _{X})$
is a metabolic linking form and
$(X,\lambda _{X})$
is a metabolic linking form and
![]() $L \subset X$
is a metabolizer for
$L \subset X$
is a metabolizer for
![]() $\lambda _{X}$
.
$\lambda _{X}$
.
In particular, if the map
![]() $H_{1}(T;{\mathbb {F}}[t^{\pm 1}]^{d}_{\gamma }) \to H_{1}(M_{P(K,\eta )};{\mathbb {F}}[t^{\pm 1}]^{d}_{\gamma })$
vanishes, then we obtain the following isometry of linking forms:
$H_{1}(T;{\mathbb {F}}[t^{\pm 1}]^{d}_{\gamma }) \to H_{1}(M_{P(K,\eta )};{\mathbb {F}}[t^{\pm 1}]^{d}_{\gamma })$
vanishes, then we obtain the following isometry of linking forms:
Proof. We first recall some notation from the proof of Theorem 3.11. Recall that we set
![]() $\mathcal {K}=~\ker (\psi )$
, where
$\mathcal {K}=~\ker (\psi )$
, where
![]() $\psi \colon \operatorname {\mathrm {Bl}}_{\gamma _P}(M_{P} \setminus \mathcal {N}(\eta )) \oplus \operatorname {\mathrm {Bl}}_{\gamma _K}(S^{3} \setminus \mathcal {N}(K)) \to \operatorname {\mathrm {Bl}}_\gamma (M_{P(K,\eta )})$
is the morphism of linking forms described in (3.4). We once again omit coefficients and recall that
$\psi \colon \operatorname {\mathrm {Bl}}_{\gamma _P}(M_{P} \setminus \mathcal {N}(\eta )) \oplus \operatorname {\mathrm {Bl}}_{\gamma _K}(S^{3} \setminus \mathcal {N}(K)) \to \operatorname {\mathrm {Bl}}_\gamma (M_{P(K,\eta )})$
is the morphism of linking forms described in (3.4). We once again omit coefficients and recall that
![]() $A:=(H_1(M_P \setminus \mathcal {N}(\eta ) )\oplus H_1(S^3 \setminus \mathcal {N}(K)))/\mathcal {K}$
. Since we saw that
$A:=(H_1(M_P \setminus \mathcal {N}(\eta ) )\oplus H_1(S^3 \setminus \mathcal {N}(K)))/\mathcal {K}$
. Since we saw that
![]() $\operatorname {\mathrm {Bl}}_{\gamma _P}(P) \oplus \operatorname {\mathrm {Bl}}_{\gamma _K}(K)$
descends to A; we let
$\operatorname {\mathrm {Bl}}_{\gamma _P}(P) \oplus \operatorname {\mathrm {Bl}}_{\gamma _K}(K)$
descends to A; we let
![]() $\operatorname {\mathrm {Bl}}_A$
denote the resulting pairing.
$\operatorname {\mathrm {Bl}}_A$
denote the resulting pairing.
Claim. There is a linking form
![]() $(X,\lambda _X)$
such that
$(X,\lambda _X)$
such that
![]() $ \operatorname {\mathrm {Bl}}_\gamma (P(K,\eta )) \cong \operatorname {\mathrm {Bl}}_{\gamma _{P}}(P) \oplus \operatorname {\mathrm {Bl}}_{\gamma _{K}}(K) \oplus (X,\lambda _X)$
.
$ \operatorname {\mathrm {Bl}}_\gamma (P(K,\eta )) \cong \operatorname {\mathrm {Bl}}_{\gamma _{P}}(P) \oplus \operatorname {\mathrm {Bl}}_{\gamma _{K}}(K) \oplus (X,\lambda _X)$
.
Proof. Using the multiplicativity of orders on the vertical exact sequence in (3.14), we see that
![]() $\operatorname {\mathrm {ord}} (A) = \operatorname {\mathrm {ord}}(\widetilde {L}) \cdot \operatorname {\mathrm {ord}}(H_{1}(M_{P})) \cdot \operatorname {\mathrm {ord}}(H_{1}(M_{K})).$
Using the primary decomposition theorem (since
$\operatorname {\mathrm {ord}} (A) = \operatorname {\mathrm {ord}}(\widetilde {L}) \cdot \operatorname {\mathrm {ord}}(H_{1}(M_{P})) \cdot \operatorname {\mathrm {ord}}(H_{1}(M_{K})).$
Using the primary decomposition theorem (since
![]() ${\mathbb {F}}[t^{\pm 1}]$
is a PID), the Chinese remainder theorem and
${\mathbb {F}}[t^{\pm 1}]$
is a PID), the Chinese remainder theorem and
![]() $\gcd (\operatorname {\mathrm {ord}} (\widetilde {L}), \operatorname {\mathrm {ord}}(H_{1}(M_{P})) \cdot \operatorname {\mathrm {ord}}(H_{1}(M_{K}))) = 1$
, we obtain an isomorphism
$\gcd (\operatorname {\mathrm {ord}} (\widetilde {L}), \operatorname {\mathrm {ord}}(H_{1}(M_{P})) \cdot \operatorname {\mathrm {ord}}(H_{1}(M_{K}))) = 1$
, we obtain an isomorphism
![]() $A \cong \widetilde {L} \oplus B,$
where B is isomorphic to
$A \cong \widetilde {L} \oplus B,$
where B is isomorphic to
![]() $H_{1}(M_{P}) \oplus H_{1}(M_{K})$
. Observe that the surjectivity of
$H_{1}(M_{P}) \oplus H_{1}(M_{K})$
. Observe that the surjectivity of
![]() $(\iota _{P})_{\ast } \oplus (\iota _{K})_{\ast }/\mathcal {K}$
implies that
$(\iota _{P})_{\ast } \oplus (\iota _{K})_{\ast }/\mathcal {K}$
implies that
Let
![]() $B' = (\psi /\mathcal {K})(B) \subset H_{1}(M_{P(K,\eta )})$
. Since
$B' = (\psi /\mathcal {K})(B) \subset H_{1}(M_{P(K,\eta )})$
. Since
![]() $\psi /\mathcal {K}$
is injective (recall (3.14)),
$\psi /\mathcal {K}$
is injective (recall (3.14)),
![]() $B \cong B'$
. By our assumptions,
$B \cong B'$
. By our assumptions,
![]() $\operatorname {\mathrm {ord}}(L)$
is relatively prime with
$\operatorname {\mathrm {ord}}(L)$
is relatively prime with
![]() $\operatorname {\mathrm {ord}}(B')$
. Furthermore, since
$\operatorname {\mathrm {ord}}(B')$
. Furthermore, since
![]() $\operatorname {\mathrm {ord}}(B')$
is symmetric, it follows that
$\operatorname {\mathrm {ord}}(B')$
is symmetric, it follows that
![]() $\gcd (\operatorname {\mathrm {ord}}(L)^{\#},\operatorname {\mathrm {ord}}(B')) = 1$
. Consequently,
$\gcd (\operatorname {\mathrm {ord}}(L)^{\#},\operatorname {\mathrm {ord}}(B')) = 1$
. Consequently,
where the first equality follows from the fact that
![]() $\operatorname {\mathrm {ord}}(H_{1}(M_{P(K,\eta )}) / B') = \operatorname {\mathrm {ord}}(L) \cdot \operatorname {\mathrm {ord}}(L)^{\#}$
. Hence, there exists a submodule
$\operatorname {\mathrm {ord}}(H_{1}(M_{P(K,\eta )}) / B') = \operatorname {\mathrm {ord}}(L) \cdot \operatorname {\mathrm {ord}}(L)^{\#}$
. Hence, there exists a submodule
![]() $X \subset H_{1}(M_{P(K,\eta )})$
, such that
$X \subset H_{1}(M_{P(K,\eta )})$
, such that
![]() $H_{1}(M_{P(K,\eta )}) = X \oplus B'$
. By [Reference Borodzik, Conway and Politarczyk3, Proposition 2.25], there is a corresponding splitting of linking forms
$H_{1}(M_{P(K,\eta )}) = X \oplus B'$
. By [Reference Borodzik, Conway and Politarczyk3, Proposition 2.25], there is a corresponding splitting of linking forms
![]() $\operatorname {\mathrm {Bl}}_{\gamma }(P(K,\eta )) = \operatorname {\mathrm {Bl}}_{\gamma }(P(K,\eta ))|_{X} \oplus \operatorname {\mathrm {Bl}}_{\gamma }(P(K,\eta ))|_{B'}$
. Since,
$\operatorname {\mathrm {Bl}}_{\gamma }(P(K,\eta )) = \operatorname {\mathrm {Bl}}_{\gamma }(P(K,\eta ))|_{X} \oplus \operatorname {\mathrm {Bl}}_{\gamma }(P(K,\eta ))|_{B'}$
. Since,
![]() $\psi /\mathcal {K} \colon A \to H_1(M_{P(K,\eta )})$
is an injective map of linking forms, we obtain identifications
$\psi /\mathcal {K} \colon A \to H_1(M_{P(K,\eta )})$
is an injective map of linking forms, we obtain identifications
where the first isomorphism is given by
![]() $(\psi / \mathcal {K})|_{B}$
and the last isomorphism follows from equation (3.15). Hence, we can take
$(\psi / \mathcal {K})|_{B}$
and the last isomorphism follows from equation (3.15). Hence, we can take
![]() $\lambda _{X} = \operatorname {\mathrm {Bl}}(P(K,\eta ))|_{X}$
, which is non-singular by [Reference Borodzik, Conway and Politarczyk3, Proposition 2.25]. This concludes the proof of the claim.
$\lambda _{X} = \operatorname {\mathrm {Bl}}(P(K,\eta ))|_{X}$
, which is non-singular by [Reference Borodzik, Conway and Politarczyk3, Proposition 2.25]. This concludes the proof of the claim.
Since Theorem 3.11 shows that
![]() $\operatorname {\mathrm {Bl}}_\gamma (M_{P(K,\eta )})$
is Witt equivalent to
$\operatorname {\mathrm {Bl}}_\gamma (M_{P(K,\eta )})$
is Witt equivalent to
![]() $\operatorname {\mathrm {Bl}}_{\gamma _P}(P) \oplus ~\operatorname {\mathrm {Bl}}_{\gamma _K}(K)$
, the claim implies that
$\operatorname {\mathrm {Bl}}_{\gamma _P}(P) \oplus ~\operatorname {\mathrm {Bl}}_{\gamma _K}(K)$
, the claim implies that
![]() $(X,\lambda _X)$
is metabolic. It remains to show that a metabolizer for
$(X,\lambda _X)$
is metabolic. It remains to show that a metabolizer for
![]() $(X,\lambda _X)$
is in fact given by
$(X,\lambda _X)$
is in fact given by
![]() $L:= (\psi /\mathcal {K})(\widetilde {L})$
. As
$L:= (\psi /\mathcal {K})(\widetilde {L})$
. As
![]() $(\psi /\mathcal {K}) \colon A \to H_1(M_{P(K,\eta )}) $
is an injective morphism of linking forms, the isomorphisms
$(\psi /\mathcal {K}) \colon A \to H_1(M_{P(K,\eta )}) $
is an injective morphism of linking forms, the isomorphisms
![]() $A \cong \widetilde {L} \oplus B$
and
$A \cong \widetilde {L} \oplus B$
and
![]() $H_1(M_{P(K,\eta )})~\cong \psi /\mathcal {K}(B) \oplus ~X$
imply that
$H_1(M_{P(K,\eta )})~\cong \psi /\mathcal {K}(B) \oplus ~X$
imply that
![]() $L = (\psi /\mathcal {K})(\widetilde {L})$
is an isotropic submodule of X. Since Theorem 3.11 shows that
$L = (\psi /\mathcal {K})(\widetilde {L})$
is an isotropic submodule of X. Since Theorem 3.11 shows that
![]() $\operatorname {\mathrm {Bl}}_{\gamma _P}(P) \oplus \operatorname {\mathrm {Bl}}_{\gamma _K}(K)$
is isometric to the isotropic reduction of
$\operatorname {\mathrm {Bl}}_{\gamma _P}(P) \oplus \operatorname {\mathrm {Bl}}_{\gamma _K}(K)$
is isometric to the isotropic reduction of
![]() $\operatorname {\mathrm {Bl}}_\gamma (M_{P(K,\eta )})$
with respect to L, the multiplicativity of orders implies that
$\operatorname {\mathrm {Bl}}_\gamma (M_{P(K,\eta )})$
with respect to L, the multiplicativity of orders implies that
![]() $\operatorname {\mathrm {ord}} (X)=\operatorname {\mathrm {ord}}(L)\operatorname {\mathrm {ord}}(L)^{\#}$
. As
$\operatorname {\mathrm {ord}} (X)=\operatorname {\mathrm {ord}}(L)\operatorname {\mathrm {ord}}(L)^{\#}$
. As
![]() ${\mathbb {F}}[t^{\pm 1}]$
is a PID, we deduce that L is a metabolizer in X, concluding the proof of the first assertion.
${\mathbb {F}}[t^{\pm 1}]$
is a PID, we deduce that L is a metabolizer in X, concluding the proof of the first assertion.
In order to prove the second assertion, notice that our hypothesis implies that the submodule L is trivial. Since L is a metabolizer of X, we deduce that X is itself trivial. The conclusion now follows from the first assertion.
The situation simplifies considerably when
![]() $\gamma _{K}$
is abelian (i.e., factors through the abelianization of
$\gamma _{K}$
is abelian (i.e., factors through the abelianization of
![]() $\pi _{1}(M_{K})$
). Let
$\pi _{1}(M_{K})$
). Let
![]() $\mathbb {F}[t_{K}^{\pm 1}]$
be the group algebra of the abelianization of
$\mathbb {F}[t_{K}^{\pm 1}]$
be the group algebra of the abelianization of
![]() $\pi _{1}(M_{K})$
with
$\pi _{1}(M_{K})$
with
![]() $t_{K}$
denoting the generator corresponding to the meridian identified with
$t_{K}$
denoting the generator corresponding to the meridian identified with
![]() $\eta $
. In this case,
$\eta $
. In this case,
![]() ${\mathbb {F}}[t^{\pm 1}]^{d}_{\gamma _{K}}$
becomes a module over
${\mathbb {F}}[t^{\pm 1}]^{d}_{\gamma _{K}}$
becomes a module over
![]() $\mathbb {F}[t_{K}^{\pm 1}]$
via the homomorphism
$\mathbb {F}[t_{K}^{\pm 1}]$
via the homomorphism
![]() $\gamma _{K} \colon \mathbb {F}[t_K^{\pm 1}] \to {\mathbb {F}}[t^{\pm 1}]^d_{\gamma _{K}} $
(i.e., via the action
$\gamma _{K} \colon \mathbb {F}[t_K^{\pm 1}] \to {\mathbb {F}}[t^{\pm 1}]^d_{\gamma _{K}} $
(i.e., via the action
![]() $t_{K} \cdot v = v\gamma _K(\eta ) $
with
$t_{K} \cdot v = v\gamma _K(\eta ) $
with
![]() $v \in {\mathbb {F}}[t^{\pm 1}]^{d}_{\gamma _{K}}$
).
$v \in {\mathbb {F}}[t^{\pm 1}]^{d}_{\gamma _{K}}$
).
In this setting, Theorem 3.11 takes the following form (compare with [Reference Friedl, Leidy, Nagel and Powell21, Theorem 1.3]).
Corollary 3.15. Using the same assumptions as in Theorem 3.11, if
![]() $\gamma _{K}$
is an abelian representation, then there exists an isometry of linking forms
$\gamma _{K}$
is an abelian representation, then there exists an isometry of linking forms
If we denote by
![]() $\mathbb {F}[\eta ] \subset \mathbb {F}[\pi (M_{P})]$
the subring generated by
$\mathbb {F}[\eta ] \subset \mathbb {F}[\pi (M_{P})]$
the subring generated by
![]() $\eta $
and we assume that
$\eta $
and we assume that
![]() $\det (\gamma _{P}(x)) \neq 0$
, for any
$\det (\gamma _{P}(x)) \neq 0$
, for any
![]() $x \in \mathbb {F}[\eta ] \setminus \{0\}$
, then
$x \in \mathbb {F}[\eta ] \setminus \{0\}$
, then
![]() $H_{1}(M_{K};{\mathbb {F}}[t^{\pm 1}]^{d}_{\gamma })$
is isomorphic to
$H_{1}(M_{K};{\mathbb {F}}[t^{\pm 1}]^{d}_{\gamma })$
is isomorphic to
![]() $H_{1}(M_{K};\mathbb {F}[t_{K}^{\pm 1}]) \otimes _{\mathbb {F}[t_{K}^{\pm 1}]} {\mathbb {F}}[t^{\pm 1}]^{d}_{\gamma _{K}},$
and there is an isometry
$H_{1}(M_{K};\mathbb {F}[t_{K}^{\pm 1}]) \otimes _{\mathbb {F}[t_{K}^{\pm 1}]} {\mathbb {F}}[t^{\pm 1}]^{d}_{\gamma _{K}},$
and there is an isometry
Proof. Let
![]() $\lambda $
denote the zero-framed longitude of K. If
$\lambda $
denote the zero-framed longitude of K. If
![]() $F \subset S^{3} \setminus \mathcal {N}(K)$
is a Seifert surface for K, then it follows that the image of
$F \subset S^{3} \setminus \mathcal {N}(K)$
is a Seifert surface for K, then it follows that the image of
![]() $\pi _{1}(F)$
is contained in the commutator subgroup of
$\pi _{1}(F)$
is contained in the commutator subgroup of
![]() $\pi _{1}(S^{3} \setminus \mathcal {N}(K))$
; therefore, the inclusion of F lifts to a map to the infinite cyclic cover of
$\pi _{1}(S^{3} \setminus \mathcal {N}(K))$
; therefore, the inclusion of F lifts to a map to the infinite cyclic cover of
![]() $S^{3} \setminus \mathcal {N}(K)$
. This means that for any
$S^{3} \setminus \mathcal {N}(K)$
. This means that for any
![]() $\mathbb {F}[t_{K}^{\pm 1}]$
-module M, the homology class of
$\mathbb {F}[t_{K}^{\pm 1}]$
-module M, the homology class of
![]() $\lambda $
is trivial in
$\lambda $
is trivial in
![]() $H_{1}(S^{3} \setminus \mathcal {N}(K);M)$
and
$H_{1}(S^{3} \setminus \mathcal {N}(K);M)$
and
![]() $H_{1}(M_{K};M)$
. Thus, the hypothesis of Corollary 3.14 is satisfied, and we therefore obtain the desired isometry of linking forms.
$H_{1}(M_{K};M)$
. Thus, the hypothesis of Corollary 3.14 is satisfied, and we therefore obtain the desired isometry of linking forms.
If we have
![]() $\det (\gamma (x))\neq 0$
for any
$\det (\gamma (x))\neq 0$
for any
![]() $x \in \mathbb {F}[\eta ] \setminus \{0\}$
, then
$x \in \mathbb {F}[\eta ] \setminus \{0\}$
, then
![]() ${\mathbb {F}}[t^{\pm 1}]^{d}_{\gamma _{K}}$
is a torsion-free
${\mathbb {F}}[t^{\pm 1}]^{d}_{\gamma _{K}}$
is a torsion-free
![]() $\mathbb {F}[t_{K}^{\pm 1}]$
-module, and hence, (since
$\mathbb {F}[t_{K}^{\pm 1}]$
-module, and hence, (since
![]() ${\mathbb {F}}[t^{\pm 1}]$
is a PID) flat
${\mathbb {F}}[t^{\pm 1}]$
is a PID) flat
![]() $\mathbb {F}[t_{K}^{\pm 1}]$
-module. The last two assertions follow easily from the flatness of
$\mathbb {F}[t_{K}^{\pm 1}]$
-module. The last two assertions follow easily from the flatness of
![]() ${\mathbb {F}}[t^{\pm 1}]^{d}_{\gamma _{K}}$
.
${\mathbb {F}}[t^{\pm 1}]^{d}_{\gamma _{K}}$
.
Next, we discuss the consequences of Theorem 3.11 on signatures of satellite knots.
Corollary 3.16. Let
![]() $P(K,\eta )$
be a satellite knot with pattern P, companion K and infection curve
$P(K,\eta )$
be a satellite knot with pattern P, companion K and infection curve
![]() $\eta $
. Let
$\eta $
. Let
![]() $\gamma \colon \pi _1(M_{P(K,\eta )}) \to GL_d({\mathbb {F}}[t^{\pm 1}])$
be a unitary acyclic
$\gamma \colon \pi _1(M_{P(K,\eta )}) \to GL_d({\mathbb {F}}[t^{\pm 1}])$
be a unitary acyclic
![]() $\eta $
-regular representation. If the assumptions of Theorem 3.11 hold, then for any
$\eta $
-regular representation. If the assumptions of Theorem 3.11 hold, then for any
![]() $\omega \in S^1$
, the averaged twisted signatures of
$\omega \in S^1$
, the averaged twisted signatures of
![]() $P(K,\eta ),P$
and K satisfy
$P(K,\eta ),P$
and K satisfy
In particular, under these assumptions, the averaged twisted signature is additive on connected sums:
Proof. Applying Theorem 3.11,
![]() $\operatorname {\mathrm {Bl}}_\gamma (P(K,\eta ))$
is Witt equivalent to
$\operatorname {\mathrm {Bl}}_\gamma (P(K,\eta ))$
is Witt equivalent to
![]() $\operatorname {\mathrm {Bl}}_{\gamma _{P}}(P) \oplus \operatorname {\mathrm {Bl}}_{\gamma _K}(K)$
. The first assertion now follows from the Witt invariance of the averaged signature; recall item (S-4) of Proposition 1.6 and compare also [Reference Borodzik, Conway and Politarczyk3, Proposition 5.7]. The second assertion is immediate since the connected sum is obtained by taking the infection curve
$\operatorname {\mathrm {Bl}}_{\gamma _{P}}(P) \oplus \operatorname {\mathrm {Bl}}_{\gamma _K}(K)$
. The first assertion now follows from the Witt invariance of the averaged signature; recall item (S-4) of Proposition 1.6 and compare also [Reference Borodzik, Conway and Politarczyk3, Proposition 5.7]. The second assertion is immediate since the connected sum is obtained by taking the infection curve
![]() $\eta $
to be the meridian of P.
$\eta $
to be the meridian of P.
Finally, in the abelian case, we recover results concerning the behavior of the Blanchfield pairing and Levine-Tristram signature under satellite operations (see [Reference Livingston and Melvin39] and [Reference Shinohara43, Reference Litherland37]).
Corollary 3.17. Let
![]() $P(K,\eta )$
be a satellite knot with pattern P, companion K, infection curve
$P(K,\eta )$
be a satellite knot with pattern P, companion K, infection curve
![]() $\eta $
and winding number
$\eta $
and winding number
![]() $w = \operatorname {\mathrm {lk}}(\eta ,P)$
. The Blanchfield pairing and Levine-Tristram signature sastify
$w = \operatorname {\mathrm {lk}}(\eta ,P)$
. The Blanchfield pairing and Levine-Tristram signature sastify
 $$ \begin{align*} \operatorname{\mathrm{Bl}}(P(K,\eta))(t)&=\operatorname{\mathrm{Bl}}(P)(t) \oplus \operatorname{\mathrm{Bl}}(K)(t^w), \\ \sigma_{P(K,\eta)}(\omega)&=\sigma_{P}(\omega)+\sigma_{K}(\omega^w). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Bl}}(P(K,\eta))(t)&=\operatorname{\mathrm{Bl}}(P)(t) \oplus \operatorname{\mathrm{Bl}}(K)(t^w), \\ \sigma_{P(K,\eta)}(\omega)&=\sigma_{P}(\omega)+\sigma_{K}(\omega^w). \end{align*} $$
4 Metabelian Representations and Casson-Gordon invariants
The aim of this section is to study signatures associated to metabelian representations. In Subsection 4.1, we recall two equivalent constructions of a ‘metabelian Blanchfield pairing’, in Subsection 4.2, we review a result due to Miller and Powell, in Subsection 4.3, we recall the definition of the Casson-Gordon
![]() $\tau $
-invariant and in Subsection 4.4, we relate it to our twisted signatures. Throughout this section, we use
$\tau $
-invariant and in Subsection 4.4, we relate it to our twisted signatures. Throughout this section, we use
![]() $\Sigma _n(K)$
to denote the n-fold cover of
$\Sigma _n(K)$
to denote the n-fold cover of
![]() $S^3$
branched along a knot K and fix a character
$S^3$
branched along a knot K and fix a character
![]() $\chi \colon H_1(\Sigma _n(K);\mathbb {Z}) \to \mathbb {Z}_m$
. We also set
$\chi \colon H_1(\Sigma _n(K);\mathbb {Z}) \to \mathbb {Z}_m$
. We also set
![]() $\xi _{m} = e^{\frac {2 \pi i}{m}}$
, and
$\xi _{m} = e^{\frac {2 \pi i}{m}}$
, and
![]() $M_K$
will always denote the 0-framed surgery along K.
$M_K$
will always denote the 0-framed surgery along K.
4.1 The metabelian Blanchfield pairing
In this subsection, we review two equivalent definitions of a particular twisted Blanchfield pairing associated to
![]() $M_K$
. The first makes use of a metabelian representation
$M_K$
. The first makes use of a metabelian representation
![]() $\alpha (n,\chi ) \colon \pi _1(M_K) \to GL_n({\mathbb {C}}[t^{\pm 1}])$
, while the second uses the n-fold cover
$\alpha (n,\chi ) \colon \pi _1(M_K) \to GL_n({\mathbb {C}}[t^{\pm 1}])$
, while the second uses the n-fold cover
![]() $M_n \to M_K$
. References for this subsection include [Reference Friedl19, Reference Herald, Kirk and Livingston28, Reference Miller and Powell40].
$M_n \to M_K$
. References for this subsection include [Reference Friedl19, Reference Herald, Kirk and Livingston28, Reference Miller and Powell40].
Use
![]() $\phi _K \colon \pi _1(M_K) \to H_1(M_K;\mathbb {Z})\cong \mathbb {Z}=\langle t_K \rangle $
to denote the abelianization homomorphism. Since
$\phi _K \colon \pi _1(M_K) \to H_1(M_K;\mathbb {Z})\cong \mathbb {Z}=\langle t_K \rangle $
to denote the abelianization homomorphism. Since
![]() $\phi _K$
endows
$\phi _K$
endows
![]() $\mathbb {Z}[t_K^{\pm 1}]$
with a right
$\mathbb {Z}[t_K^{\pm 1}]$
with a right
![]() $\pi _1(M_K)$
-module structure, it gives rise to the twisted homology
$\pi _1(M_K)$
-module structure, it gives rise to the twisted homology
![]() $\mathbb {Z}[t_K^{\pm 1}]$
-module
$\mathbb {Z}[t_K^{\pm 1}]$
-module
![]() $H_1(M_K;\mathbb {Z}[t_{K}^{\pm 1}])$
. This module is known to coincide with the Alexander module of K. In what follows, we shall frequently identify
$H_1(M_K;\mathbb {Z}[t_{K}^{\pm 1}])$
. This module is known to coincide with the Alexander module of K. In what follows, we shall frequently identify
![]() $H_1(\Sigma _n(K);\mathbb {Z})$
with
$H_1(\Sigma _n(K);\mathbb {Z})$
with
![]() $H_1(M_K;\mathbb {Z}[t_K^{\pm 1}])/(t_K^n-1)$
as in [Reference Friedl and Powell23, Corollary 2.4]. We now consider the semidirect product
$H_1(M_K;\mathbb {Z}[t_K^{\pm 1}])/(t_K^n-1)$
as in [Reference Friedl and Powell23, Corollary 2.4]. We now consider the semidirect product
![]() $\mathbb {Z} \ltimes H_1(\Sigma _n(K);\mathbb {Z})$
, where the group law is given by
$\mathbb {Z} \ltimes H_1(\Sigma _n(K);\mathbb {Z})$
, where the group law is given by
![]() $ (t_K^i,v)\cdot (t_K^j,w)=(t_K^{i+j},t_K^{-j}v+w)$
. Next, consider the representation
$ (t_K^i,v)\cdot (t_K^j,w)=(t_K^{i+j},t_K^{-j}v+w)$
. Next, consider the representation
 $$ \begin{align} \gamma_K(n,\chi) \colon \mathbb{Z} \ltimes H_1(\Sigma_n(K);\mathbb{Z}) &\to ~\operatorname{GL}_n({\mathbb{C}}[t^{\pm 1}]) \nonumber \\ (t_K^j,v) &\mapsto \begin{pmatrix} 0& 1 & \cdots &0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \\ t & 0 & \cdots & 0 \end{pmatrix}^j \begin{pmatrix} \xi_{m}^{\chi(v)} & 0 & \cdots &0 \\ 0 & \xi_{m}^{\chi(t_K \cdot v)} & \cdots &0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \xi_{m}^{\chi(t_K^{n-1} \cdot v)} \end{pmatrix}. \end{align} $$
$$ \begin{align} \gamma_K(n,\chi) \colon \mathbb{Z} \ltimes H_1(\Sigma_n(K);\mathbb{Z}) &\to ~\operatorname{GL}_n({\mathbb{C}}[t^{\pm 1}]) \nonumber \\ (t_K^j,v) &\mapsto \begin{pmatrix} 0& 1 & \cdots &0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \\ t & 0 & \cdots & 0 \end{pmatrix}^j \begin{pmatrix} \xi_{m}^{\chi(v)} & 0 & \cdots &0 \\ 0 & \xi_{m}^{\chi(t_K \cdot v)} & \cdots &0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \xi_{m}^{\chi(t_K^{n-1} \cdot v)} \end{pmatrix}. \end{align} $$
We will now use
![]() $\gamma _K(n,\chi )$
to obtain a representation of
$\gamma _K(n,\chi )$
to obtain a representation of
![]() $\pi _1(M_K)$
. To achieve this, we identify the Alexander module
$\pi _1(M_K)$
. To achieve this, we identify the Alexander module
![]() $H_1(M_K;\mathbb {Z}[t_{K}^{\pm 1}])$
with the derived quotient
$H_1(M_K;\mathbb {Z}[t_{K}^{\pm 1}])$
with the derived quotient
![]() $\pi _1(M_K)^{(1)}/\pi _1(M_K)^{(2)}$
and consider the following composition of canonical projections:
$\pi _1(M_K)^{(1)}/\pi _1(M_K)^{(2)}$
and consider the following composition of canonical projections:
Fix an element
![]() $\mu _{K}$
in
$\mu _{K}$
in
![]() $\pi _1(M_K)$
such that
$\pi _1(M_K)$
such that
![]() $\phi _K(\mu _{K})=t_K$
. Note that for every
$\phi _K(\mu _{K})=t_K$
. Note that for every
![]() $g \in \pi _1(M_K)$
, we have
$g \in \pi _1(M_K)$
, we have
![]() $\phi _K(\mu _K^{-\phi _K(g)}g)=1$
. Since
$\phi _K(\mu _K^{-\phi _K(g)}g)=1$
. Since
![]() $\phi _K$
is the abelianization map, we deduce that
$\phi _K$
is the abelianization map, we deduce that
![]() $\mu _K^{-\phi _K(g)}g$
belongs to
$\mu _K^{-\phi _K(g)}g$
belongs to
![]() $\pi _1(M_K)^{(1)}$
. As a consequence, we obtain the following map:
$\pi _1(M_K)^{(1)}$
. As a consequence, we obtain the following map:
 $$ \begin{align} \widetilde{\rho}_K \colon \pi_1(M_K) &\to \mathbb{Z} \ltimes H_1(\Sigma_n(K);\mathbb{Z}) \\ g &\mapsto (\phi_K(g),q_K(\mu_{K}^{-\phi_K(g)}g)). \nonumber \end{align} $$
$$ \begin{align} \widetilde{\rho}_K \colon \pi_1(M_K) &\to \mathbb{Z} \ltimes H_1(\Sigma_n(K);\mathbb{Z}) \\ g &\mapsto (\phi_K(g),q_K(\mu_{K}^{-\phi_K(g)}g)). \nonumber \end{align} $$
Precomposing the representation
![]() $\gamma _K(n,\chi )$
with
$\gamma _K(n,\chi )$
with
![]() $\widetilde {\rho }_K$
provides the unitary representation
$\widetilde {\rho }_K$
provides the unitary representation
If m is a prime power and
![]() $\chi \colon H_1(\Sigma _n(K);\mathbb {Z}) \to \mathbb {Z}_m$
is nontrivial, it is known that the unitary representation
$\chi \colon H_1(\Sigma _n(K);\mathbb {Z}) \to \mathbb {Z}_m$
is nontrivial, it is known that the unitary representation
![]() $\alpha (n,\chi )$
is acyclic [Reference Friedl and Powell22] (see also [Reference Miller and Powell40, Lemma 6.6] and [Reference Casson and Gordon6, Corollary following Lemma 4]). When the knot K is clear from the context, we drop it from the notation and simply write
$\alpha (n,\chi )$
is acyclic [Reference Friedl and Powell22] (see also [Reference Miller and Powell40, Lemma 6.6] and [Reference Casson and Gordon6, Corollary following Lemma 4]). When the knot K is clear from the context, we drop it from the notation and simply write
![]() $\alpha (n,\chi )$
instead of
$\alpha (n,\chi )$
instead of
![]() $\alpha _K(n,\chi )$
.
$\alpha _K(n,\chi )$
.
The next lemma illustrates this notation and will be used to ensure that the hypotheses of Theorem 3.11 hold.
Lemma 4.1. If
![]() $\chi \colon H_1(\Sigma _n(K);\mathbb {Z}) \to \mathbb {Z}_m$
is nontrivial, then
$\chi \colon H_1(\Sigma _n(K);\mathbb {Z}) \to \mathbb {Z}_m$
is nontrivial, then
![]() $H_0(M_K;{\mathbb {C}}[t^{\pm 1}]_{\alpha (n,\chi )}^n)=0$
.
$H_0(M_K;{\mathbb {C}}[t^{\pm 1}]_{\alpha (n,\chi )}^n)=0$
.
Proof. Let
![]() $e_{i} \in \mathbb {C}[t^{\pm 1}]^{n}$
, for
$e_{i} \in \mathbb {C}[t^{\pm 1}]^{n}$
, for
![]() $i=1,2,\ldots ,n$
, denote the vectors from the standard basis. By definition,
$i=1,2,\ldots ,n$
, denote the vectors from the standard basis. By definition,
![]() $H_0(M_K;{\mathbb {C}}[t^{\pm 1}]_{\alpha (n,\chi )}^n)={\mathbb {C}}[t^{\pm 1}]^n/V$
, with
$H_0(M_K;{\mathbb {C}}[t^{\pm 1}]_{\alpha (n,\chi )}^n)={\mathbb {C}}[t^{\pm 1}]^n/V$
, with
Therefore, it is sufficient to prove that for any
![]() $1 \leq i \leq n$
, there exists
$1 \leq i \leq n$
, there exists
![]() $g_{i} \in \pi _{1}(M_{K})$
and
$g_{i} \in \pi _{1}(M_{K})$
and
![]() $w_{i} \in \mathbb {C}[t^{\pm 1}]^{n}$
so that
$w_{i} \in \mathbb {C}[t^{\pm 1}]^{n}$
so that
![]() $e_{i} = \left (\alpha (n,\chi )(g_{i}) - \operatorname {id}\right ) \cdot w_{i}$
. Fix
$e_{i} = \left (\alpha (n,\chi )(g_{i}) - \operatorname {id}\right ) \cdot w_{i}$
. Fix
![]() $1 \leq i \leq n$
. Choose any
$1 \leq i \leq n$
. Choose any
![]() $h_{i} \in [\pi _{1}(M_{K}),\pi _{1}(M_{K})]$
so that
$h_{i} \in [\pi _{1}(M_{K}),\pi _{1}(M_{K})]$
so that
![]() $\chi (\widetilde {\rho }_K(h_{i})) \neq 1$
; such an
$\chi (\widetilde {\rho }_K(h_{i})) \neq 1$
; such an
![]() $h_i$
exists because
$h_i$
exists because
![]() $\chi $
is nontrivial and
$\chi $
is nontrivial and
![]() $\widetilde {\rho }_K$
is surjective. The definition of
$\widetilde {\rho }_K$
is surjective. The definition of
![]() $\alpha (n,\chi )$
then gives
$\alpha (n,\chi )$
then gives
Therefore, for
![]() $g_{i} := \mu _K^{-i+1} \cdot h_{i} \cdot \mu _K^{i-1}$
and
$g_{i} := \mu _K^{-i+1} \cdot h_{i} \cdot \mu _K^{i-1}$
and
![]() $w_{i} := \frac {1}{\chi (\widetilde {\rho }_K(h_{i}))-1} e_{i}$
, we have
$w_{i} := \frac {1}{\chi (\widetilde {\rho }_K(h_{i}))-1} e_{i}$
, we have
![]() $e_{i} = \left (\alpha (n,\chi )(g_{i}) - \operatorname {id}\right ) \cdot w_{i}$
.
$e_{i} = \left (\alpha (n,\chi )(g_{i}) - \operatorname {id}\right ) \cdot w_{i}$
.
We now use
![]() $\alpha (n,\chi )$
to endow
$\alpha (n,\chi )$
to endow
![]() $\mathbb {C}[t^{\pm 1}]^n$
with a right
$\mathbb {C}[t^{\pm 1}]^n$
with a right
![]() $\mathbb {Z}[\pi _1(M_K)]$
-module structure and apply Definition 2.2 to define a twisted Blanchfield pairing on
$\mathbb {Z}[\pi _1(M_K)]$
-module structure and apply Definition 2.2 to define a twisted Blanchfield pairing on
![]() $M_K$
.
$M_K$
.
Definition 4.2. Let K be an oriented knot, n be an integer and m be a prime power, and choose a nontrivial character
![]() $\chi \colon H_1(\Sigma _n(K);\mathbb {Z}) \to ~\mathbb {Z}_m$
. The metabelian Blanchfield pairing is the Blanchfield pairing twisted by the unitary acyclic representation
$\chi \colon H_1(\Sigma _n(K);\mathbb {Z}) \to ~\mathbb {Z}_m$
. The metabelian Blanchfield pairing is the Blanchfield pairing twisted by the unitary acyclic representation
![]() $\alpha (n,\chi )$
:
$\alpha (n,\chi )$
:
Next, we provide a description of
![]() $\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(K)$
in terms of the n-fold cyclic cover
$\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(K)$
in terms of the n-fold cyclic cover
![]() $p \colon M_n \to M_K$
. The first step is to consider the abelian subgroup
$p \colon M_n \to M_K$
. The first step is to consider the abelian subgroup
![]() $n\mathbb {Z} \times H_1(\Sigma _n(K);\mathbb {Z})$
of
$n\mathbb {Z} \times H_1(\Sigma _n(K);\mathbb {Z})$
of
![]() $\mathbb {Z} \ltimes H_1(\Sigma _n(K);\mathbb {Z})$
and the following
$\mathbb {Z} \ltimes H_1(\Sigma _n(K);\mathbb {Z})$
and the following
![]() $1$
-dimensional representation:
$1$
-dimensional representation:
 $$ \begin{align} \rho_K(n,\chi) \colon n \mathbb{Z} \times H_1(\Sigma_n(K);\mathbb{Z}) &\to {\mathbb{C}}[t^{\pm 1}] \\ (t_K^{nk},v) &\mapsto t^k \xi_{m}^{\chi(v)}. \nonumber \end{align} $$
$$ \begin{align} \rho_K(n,\chi) \colon n \mathbb{Z} \times H_1(\Sigma_n(K);\mathbb{Z}) &\to {\mathbb{C}}[t^{\pm 1}] \\ (t_K^{nk},v) &\mapsto t^k \xi_{m}^{\chi(v)}. \nonumber \end{align} $$
We now use
![]() $\rho _K(n,\chi )$
to obtain a representation of
$\rho _K(n,\chi )$
to obtain a representation of
![]() $\pi _1(M_n)$
. Consider the composition
$\pi _1(M_n)$
. Consider the composition
![]() $\pi _1(M_n) \stackrel {p_*}{\rightarrow } \pi _1(M_K) \to H_1(M_K;\mathbb {Z}) \cong \mathbb {Z}$
. Since the image of this map is isomorphic to
$\pi _1(M_n) \stackrel {p_*}{\rightarrow } \pi _1(M_K) \to H_1(M_K;\mathbb {Z}) \cong \mathbb {Z}$
. Since the image of this map is isomorphic to
![]() $n \mathbb {Z}$
, mapping to it produces a surjective map
$n \mathbb {Z}$
, mapping to it produces a surjective map
![]() $\alpha \colon \pi _1(M_n) \to n \mathbb {Z}$
. Using the decomposition
$\alpha \colon \pi _1(M_n) \to n \mathbb {Z}$
. Using the decomposition
![]() $H_1(M_n;\mathbb {Z}) \cong H_1(\Sigma _n(K);\mathbb {Z}) \oplus ~\mathbb {Z}$
additionally gives rise to a homomorphism
$H_1(M_n;\mathbb {Z}) \cong H_1(\Sigma _n(K);\mathbb {Z}) \oplus ~\mathbb {Z}$
additionally gives rise to a homomorphism
![]() $\rho \colon \pi _1(M_n) \to H_1(\Sigma _n(K);\mathbb {Z})$
. Consider the
$\rho \colon \pi _1(M_n) \to H_1(\Sigma _n(K);\mathbb {Z})$
. Consider the
![]() $\mathbb {Z}[\pi _1(M_n)]$
-module structure on
$\mathbb {Z}[\pi _1(M_n)]$
-module structure on
![]() $\mathbb {C}[t^{\pm 1}]$
given by the following composition:
$\mathbb {C}[t^{\pm 1}]$
given by the following composition:
Under the assumption that m is a prime power and that
![]() $\chi $
is a nontrivial character, Casson and Gordon show that
$\chi $
is a nontrivial character, Casson and Gordon show that
![]() $H_*(M_n;\mathbb {C}(t))$
vanishes [Reference Casson and Gordon6, Corollary after Lemma 4]. In other words, under these conditions, the unitary representation
$H_*(M_n;\mathbb {C}(t))$
vanishes [Reference Casson and Gordon6, Corollary after Lemma 4]. In other words, under these conditions, the unitary representation
![]() $\alpha \times \chi $
is acyclic.
$\alpha \times \chi $
is acyclic.
Definition 4.3. Let n be an integer, let m be a prime power and let
![]() $\chi \colon H_1(\Sigma _n(K);\mathbb {Z}) \to \mathbb {Z}_m$
be a nontrivial character. The Blanchfield pairing of the cover
$\chi \colon H_1(\Sigma _n(K);\mathbb {Z}) \to \mathbb {Z}_m$
be a nontrivial character. The Blanchfield pairing of the cover
![]() $\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(M_n)$
is the Blanchfield pairing corresponding to the unitary acyclic representation
$\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(M_n)$
is the Blanchfield pairing corresponding to the unitary acyclic representation
![]() $\alpha \times \chi :$
$\alpha \times \chi :$
Up to the end of this subsection, we shall use
![]() ${\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi }$
to denote the
${\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi }$
to denote the
![]() $\mathbb {Z}[\pi _1(M_n)]$
-module structure on
$\mathbb {Z}[\pi _1(M_n)]$
-module structure on
![]() ${\mathbb {C}}[t^{\pm 1}]$
given by (4.5) and by
${\mathbb {C}}[t^{\pm 1}]$
given by (4.5) and by
![]() ${\mathbb {C}}[t^{\pm 1}]^n_{\alpha (n,\chi )}$
the
${\mathbb {C}}[t^{\pm 1}]^n_{\alpha (n,\chi )}$
the
![]() $\mathbb {Z}[\pi _1(M_K)]$
-module structure on
$\mathbb {Z}[\pi _1(M_K)]$
-module structure on
![]() ${\mathbb {C}}[t^{\pm 1}]^n$
given by (4.3). The following result is due to Herald, Kirk and Livingston [Reference Herald, Kirk and Livingston28, Theorem 7.1].
${\mathbb {C}}[t^{\pm 1}]^n$
given by (4.3). The following result is due to Herald, Kirk and Livingston [Reference Herald, Kirk and Livingston28, Theorem 7.1].
Proposition 4.4. Let n be a positive integer. There is a canonical chain isomorphism of left
![]() ${\mathbb {C}}[t^{\pm 1}]$
-modules between
${\mathbb {C}}[t^{\pm 1}]$
-modules between
![]() $C_*(M_n;\mathbb {C}[t^{\pm 1}]_{\alpha \times \chi })$
and
$C_*(M_n;\mathbb {C}[t^{\pm 1}]_{\alpha \times \chi })$
and
![]() $C_*(M_K;\mathbb {C}[t^{\pm 1}]^n_{\alpha (n,\chi )})$
. In particular, one obtains a canonical isomorphism between the following homology left
$C_*(M_K;\mathbb {C}[t^{\pm 1}]^n_{\alpha (n,\chi )})$
. In particular, one obtains a canonical isomorphism between the following homology left
![]() ${\mathbb {C}}[t^{\pm 1}]$
-modules:
${\mathbb {C}}[t^{\pm 1}]$
-modules:
The proof of Proposition 4.4 relies on the relation between the representation
![]() $\gamma _K(n,\chi )$
of (4.1) and the representation
$\gamma _K(n,\chi )$
of (4.1) and the representation
![]() $\rho _K(n,\chi )$
of (4.4). Since we shall use this relation in Subsection 4.5, we give some further details.
$\rho _K(n,\chi )$
of (4.4). Since we shall use this relation in Subsection 4.5, we give some further details.
Remark 4.5. Let H be a subgroup of a group G and let
![]() $\rho $
be a representation of H. It is known that there is an induced representation
$\rho $
be a representation of H. It is known that there is an induced representation
![]() $\operatorname {ind}_H^G\rho $
of G; we refer to [Reference Herald, Kirk and Livingston28] for a construction and a discussion of its properties. Taking
$\operatorname {ind}_H^G\rho $
of G; we refer to [Reference Herald, Kirk and Livingston28] for a construction and a discussion of its properties. Taking
![]() $G=\mathbb {Z} \ltimes H_1(\Sigma _n(K);\mathbb {Z})$
and
$G=\mathbb {Z} \ltimes H_1(\Sigma _n(K);\mathbb {Z})$
and
![]() $H=n\mathbb {Z} \times H_1(\Sigma _n(K);\mathbb {Z})$
, the proof of Proposition 4.4 relies heavily on the isomorphism
$H=n\mathbb {Z} \times H_1(\Sigma _n(K);\mathbb {Z})$
, the proof of Proposition 4.4 relies heavily on the isomorphism
As the isomorphism described in (4.7) arises from a canonical chain isomorphism (essentially Shapiro’s lemma), we obtain the following result which appears to be implicit in [Reference Miller and Powell40]. However, since no proof has appeared in the literature, we will give a detailed argument in the appendix, and, in particular, this corollary will follow from the more general Proposition A.11.
Corollary 4.6. The isomorphism described in (4.7) gives rise to an isometry between the twisted Blanchfield pairings
![]() $\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(M_n)$
and
$\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(M_n)$
and
![]() $ \operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(K)$
.
$ \operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(K)$
.
Summarizing the content of this section, we can choose to work alternatively with
![]() $\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(K)$
or with
$\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(K)$
or with
![]() $\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(M_n)$
. The former is used in the paper of Miller-Powell [Reference Miller and Powell40] as well as in Subsections 4.2 and 4.5, and in [Reference Borodzik, Conway and Politarczyk2]. The latter is closer to the definition of the Casson-Gordon
$\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(M_n)$
. The former is used in the paper of Miller-Powell [Reference Miller and Powell40] as well as in Subsections 4.2 and 4.5, and in [Reference Borodzik, Conway and Politarczyk2]. The latter is closer to the definition of the Casson-Gordon
![]() $\tau $
invariant with which we shall work in Subsections 4.3 and 4.4.
$\tau $
invariant with which we shall work in Subsections 4.3 and 4.4.
4.2 A sliceness obstruction due to Miller and Powell
The aim of this subsection is to state an obstruction to sliceness which is due to Miller and Powell [Reference Miller and Powell40].
Given an integer n, we use
![]() $\lambda _n$
to denote the non-singular
$\lambda _n$
to denote the non-singular
![]() $\mathbb {Q}/\mathbb {Z}$
-valued linking form on the finite abelian group
$\mathbb {Q}/\mathbb {Z}$
-valued linking form on the finite abelian group
![]() $H_1(\Sigma _n(K);\mathbb {Z})$
. Note that
$H_1(\Sigma _n(K);\mathbb {Z})$
. Note that
![]() $H_1(\Sigma _n(K);\mathbb {Z})$
is also a
$H_1(\Sigma _n(K);\mathbb {Z})$
is also a
![]() $\mathbb {Z}[\mathbb {Z}_n]$
-module. A metabolizer of
$\mathbb {Z}[\mathbb {Z}_n]$
-module. A metabolizer of
![]() $\lambda _n$
is a
$\lambda _n$
is a
![]() $\mathbb {Z}[\mathbb {Z}_n]$
-submodule P of
$\mathbb {Z}[\mathbb {Z}_n]$
-submodule P of
![]() $H_1(\Sigma _n(K);\mathbb {Z})$
such that
$H_1(\Sigma _n(K);\mathbb {Z})$
such that
![]() $P=P^\perp $
, where the orthogonal complement is defined as
$P=P^\perp $
, where the orthogonal complement is defined as
![]() $P^\perp =\{y\in H_1(\Sigma _n(K);\mathbb {Z})\ | \ \forall x\in P,\ \lambda _n(x,y)=~0\}$
. Finally, given a prime q, integers
$P^\perp =\{y\in H_1(\Sigma _n(K);\mathbb {Z})\ | \ \forall x\in P,\ \lambda _n(x,y)=~0\}$
. Finally, given a prime q, integers
![]() $b \geq a$
and a character
$b \geq a$
and a character
![]() $\chi \colon H_1(\Sigma _n(K);\mathbb {Z}) \to ~\mathbb {Z}_{q^a}$
, we use
$\chi \colon H_1(\Sigma _n(K);\mathbb {Z}) \to ~\mathbb {Z}_{q^a}$
, we use
![]() $\chi _b$
to denote the composition of
$\chi _b$
to denote the composition of
![]() $\chi $
with the natural inclusion
$\chi $
with the natural inclusion
![]() $\mathbb {Z}_{q^a} \to \mathbb {Z}_{q^b}$
.
$\mathbb {Z}_{q^a} \to \mathbb {Z}_{q^b}$
.
The following obstruction to sliceness is due to Miller and Powell [Reference Miller and Powell40, Theorem 6.9].
Theorem 4.7. Let K be a slice knot. Then, for any prime power n, there exists a metabolizer P of
![]() $\lambda _n$
such that for any prime power
$\lambda _n$
such that for any prime power
![]() $q^a$
, and any nontrivial character
$q^a$
, and any nontrivial character
![]() $\chi \colon H_1(\Sigma _n(K);\mathbb {Z}) \to \mathbb {Z}_{q^a}$
vanishing on P, we have some
$\chi \colon H_1(\Sigma _n(K);\mathbb {Z}) \to \mathbb {Z}_{q^a}$
vanishing on P, we have some
![]() $b \geq a$
such that the metabelian Blanchfield pairing
$b \geq a$
such that the metabelian Blanchfield pairing
![]() $Bl_{\alpha (n,\chi _b)}(K)$
is metabolic.
$Bl_{\alpha (n,\chi _b)}(K)$
is metabolic.
Miller and Powell actually prove Theorem 4.7 under the weaker assumption that K is 2-solvable. We refer to Cochran-Orr-Teichner’s landmark paper [Reference Cochran, Orr and Teichner9] for the definition of n-solvability but do not delve deeper into this issue.
Combining Theorem 4.7 with the earlier sections, we obtain the following result.
Theorem 4.8. Let K be a slice knot. Then, for any prime power n, there exists a metabolizer P of
![]() $\lambda _n$
such that for any prime power
$\lambda _n$
such that for any prime power
![]() $q^a$
, and any nontrivial character
$q^a$
, and any nontrivial character
![]() $\chi \colon H_1(\Sigma _n(K);\mathbb {Z}) \to \mathbb {Z}_{q^a}$
vanishing on P, we have some
$\chi \colon H_1(\Sigma _n(K);\mathbb {Z}) \to \mathbb {Z}_{q^a}$
vanishing on P, we have some
![]() $b \geq a$
such that the signature function
$b \geq a$
such that the signature function
![]() $\sigma ^{av}_{K,\alpha (n,\chi _b)}$
is zero.
$\sigma ^{av}_{K,\alpha (n,\chi _b)}$
is zero.
Proof. Theorem 4.7 implies that
![]() $\operatorname {\mathrm {Bl}}_{\alpha (k,\chi _b)}(K)$
is metabolic. Consequently, item (S-4) of Proposition 1.6 implies that the averaged signature function of
$\operatorname {\mathrm {Bl}}_{\alpha (k,\chi _b)}(K)$
is metabolic. Consequently, item (S-4) of Proposition 1.6 implies that the averaged signature function of
![]() $\operatorname {\mathrm {Bl}}_{\alpha (n,\chi _b)}(K)$
vanishes.
$\operatorname {\mathrm {Bl}}_{\alpha (n,\chi _b)}(K)$
vanishes.
The obstruction of Theorem 4.7 is used in [Reference Borodzik, Conway and Politarczyk2] to prove that a certain algebraic knot is not slice, thus recovering a result of Hedden-Kirk-Livingston [Reference Hedden, Kirk and Livingston27].
4.3 The Casson-Gordon
 $\tau $
-invariant
$\tau $
-invariant
Given an oriented knot K and a prime power order character
![]() $\chi \colon H_1(\Sigma _n(K);\mathbb {Z}) \to \mathbb {Z}_m$
, we recall Casson-Gordon’s construction of the Witt class
$\chi \colon H_1(\Sigma _n(K);\mathbb {Z}) \to \mathbb {Z}_m$
, we recall Casson-Gordon’s construction of the Witt class
![]() $\tau (K,\chi )$
[Reference Casson and Gordon6].
$\tau (K,\chi )$
[Reference Casson and Gordon6].
Using the isomorphism
![]() $ H_1(M_n;\mathbb {Z}) \cong H_1(\Sigma _n(K);\mathbb {Z}) \oplus \mathbb {Z}$
, the character
$ H_1(M_n;\mathbb {Z}) \cong H_1(\Sigma _n(K);\mathbb {Z}) \oplus \mathbb {Z}$
, the character
![]() $\chi $
induces a character on
$\chi $
induces a character on
![]() $H_1(M_n;\mathbb {Z})$
for which we use the same notation. Recalling that the projection
$H_1(M_n;\mathbb {Z})$
for which we use the same notation. Recalling that the projection
![]() $p \colon M_n \to M_K$
gives rise to a surjection
$p \colon M_n \to M_K$
gives rise to a surjection
![]() $\alpha \colon \pi _1(M_n) \to n\mathbb {Z} \cong \mathbb {Z}$
, we obtain a homomorphism
$\alpha \colon \pi _1(M_n) \to n\mathbb {Z} \cong \mathbb {Z}$
, we obtain a homomorphism
Since the bordism group
![]() $\Omega _3(\mathbb {Z} \times \mathbb {Z}_m)$
is finite (this can be seen using the Atiyah-Hirzbruch spectral sequence; see, for example, [Reference Conner and Floyd11, Chapter 1, Section 7]), there is an integer r such that r copies of
$\Omega _3(\mathbb {Z} \times \mathbb {Z}_m)$
is finite (this can be seen using the Atiyah-Hirzbruch spectral sequence; see, for example, [Reference Conner and Floyd11, Chapter 1, Section 7]), there is an integer r such that r copies of
![]() $(M_n,\alpha \times \chi )$
bound
$(M_n,\alpha \times \chi )$
bound
![]() $(V_n,\psi )$
for some
$(V_n,\psi )$
for some
![]() $4$
-manifold
$4$
-manifold
![]() $V_n$
and for some homomorphism
$V_n$
and for some homomorphism
![]() $\psi \colon \pi _1(V_n) \to \mathbb {Z} \times \mathbb {Z}_m$
. Consider the map
$\psi \colon \pi _1(V_n) \to \mathbb {Z} \times \mathbb {Z}_m$
. Consider the map
![]() $\mathbb {C}[\mathbb {Z} \times \mathbb {Z}_m] \to \mathbb {C}[t^{\pm 1}]$
which sends the generator of
$\mathbb {C}[\mathbb {Z} \times \mathbb {Z}_m] \to \mathbb {C}[t^{\pm 1}]$
which sends the generator of
![]() $\mathbb {Z}_m$
to
$\mathbb {Z}_m$
to
![]() $\xi _{m} = e^{2\pi i/m}$
and the generator of
$\xi _{m} = e^{2\pi i/m}$
and the generator of
![]() $\mathbb {Z}$
to t. Endow
$\mathbb {Z}$
to t. Endow
![]() $\mathbb {C}(t)$
with the right
$\mathbb {C}(t)$
with the right
![]() $\mathbb {Z}[\pi _1(V_n)]$
-module structure which arises from the composition
$\mathbb {Z}[\pi _1(V_n)]$
-module structure which arises from the composition
We will denote by
![]() $\mathbb {C}(t)_{\alpha \times \chi }$
the module
$\mathbb {C}(t)_{\alpha \times \chi }$
the module
![]() $\mathbb {C}(t)$
equipped with the action of the group ring
$\mathbb {C}(t)$
equipped with the action of the group ring
![]() $\mathbb {Z}[\pi _1(V_n)]$
as described above. Observe that (4.9) also provides a right
$\mathbb {Z}[\pi _1(V_n)]$
as described above. Observe that (4.9) also provides a right
![]() $\mathbb {Z}[\pi _1(V_n)]$
-module structure on
$\mathbb {Z}[\pi _1(V_n)]$
-module structure on
![]() ${\mathbb {C}}[t^{\pm 1}]$
(we write
${\mathbb {C}}[t^{\pm 1}]$
(we write
![]() ${\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi }$
) which restricts to the one described in (4.5) on each boundary component of
${\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi }$
) which restricts to the one described in (4.5) on each boundary component of
![]() $V_n$
. We will denote the related
$V_n$
. We will denote the related
![]() $\mathbb {C}[\mathbb {Z}\times \mathbb {Z}_{m}]$
-module by
$\mathbb {C}[\mathbb {Z}\times \mathbb {Z}_{m}]$
-module by
![]() ${\mathbb {C}}[t^{\pm 1}]_{\mathbb {Z} \times \mathbb {Z}_m}$
. Next, consider the
${\mathbb {C}}[t^{\pm 1}]_{\mathbb {Z} \times \mathbb {Z}_m}$
. Next, consider the
![]() $\mathbb {C}(t)$
-valued intersection form
$\mathbb {C}(t)$
-valued intersection form
![]() $\lambda _{\mathbb {C}(t)_{\alpha \times \chi },V_n}$
on
$\lambda _{\mathbb {C}(t)_{\alpha \times \chi },V_n}$
on
![]() $H_2(V_n;\mathbb {C}(t)_{\alpha \times \chi })$
. Casson and Gordon show that if
$H_2(V_n;\mathbb {C}(t)_{\alpha \times \chi })$
. Casson and Gordon show that if
![]() $\chi $
is a character of prime power order, then this Hermitian form is non-singular [Reference Casson and Gordon6, Corollary following Lemma 4]. We record this result for later reference.
$\chi $
is a character of prime power order, then this Hermitian form is non-singular [Reference Casson and Gordon6, Corollary following Lemma 4]. We record this result for later reference.
Lemma 4.9. Let n be an integer and let m be a prime power. If
![]() $\chi $
is a nontrivial character, then
$\chi $
is a nontrivial character, then
![]() $H_*(M_n;\mathbb {C}(t)_{\alpha \times \chi })=0$
and the intersection pairing
$H_*(M_n;\mathbb {C}(t)_{\alpha \times \chi })=0$
and the intersection pairing
![]() $\lambda _{\mathbb {C}(t)_{\alpha \times \chi },V_n}$
is non-singular.
$\lambda _{\mathbb {C}(t)_{\alpha \times \chi },V_n}$
is non-singular.
Since
![]() $\lambda _{\mathbb {C}(t)_{\alpha \times \chi },V_n}$
is non-singular, it gives rise to a Witt class
$\lambda _{\mathbb {C}(t)_{\alpha \times \chi },V_n}$
is non-singular, it gives rise to a Witt class
![]() $[\lambda _{\mathbb {C}(t)_{\alpha \times \chi },V_n}]$
in
$[\lambda _{\mathbb {C}(t)_{\alpha \times \chi },V_n}]$
in
![]() $W(\mathbb {C}(t))$
. However, the standard intersection pairing
$W(\mathbb {C}(t))$
. However, the standard intersection pairing
![]() $\lambda _{\mathbb {Q},V_n}$
may very well be singular. Consequently, we use
$\lambda _{\mathbb {Q},V_n}$
may very well be singular. Consequently, we use
![]() $\lambda _{\mathbb {Q},V_n}^{\text {nonsing}}$
to denote the form obtained by moding out the radical. The Witt class of
$\lambda _{\mathbb {Q},V_n}^{\text {nonsing}}$
to denote the form obtained by moding out the radical. The Witt class of
![]() $\lambda _{\mathbb {Q},V_n}^{\text {nonsing}}$
provides an element in
$\lambda _{\mathbb {Q},V_n}^{\text {nonsing}}$
provides an element in
![]() $W(\mathbb {Q})$
. Since the inclusion map
$W(\mathbb {Q})$
. Since the inclusion map
![]() $\mathbb {Q} \to \mathbb {C}(t)$
induces a group homomorphism
$\mathbb {Q} \to \mathbb {C}(t)$
induces a group homomorphism
![]() $i \colon W(\mathbb {Q}) \to W(\mathbb {C}(t))$
, we therefore obtain an element
$i \colon W(\mathbb {Q}) \to W(\mathbb {C}(t))$
, we therefore obtain an element
![]() $i([\lambda _{\mathbb {Q},V_n}^{\text {nonsing}}])$
in
$i([\lambda _{\mathbb {Q},V_n}^{\text {nonsing}}])$
in
![]() $W(\mathbb {C}(t))$
.
$W(\mathbb {C}(t))$
.
Definition 4.10. Let K be an oriented knot, let n be an integer, let m be a prime power and let
![]() $\chi \colon H_1(\Sigma _n(K);\mathbb {Z}) \to \mathbb {Z}_m$
be a nontrivial character. The Casson-Gordon
$\chi \colon H_1(\Sigma _n(K);\mathbb {Z}) \to \mathbb {Z}_m$
be a nontrivial character. The Casson-Gordon
![]() $\tau $
-invariant is the Witt class
$\tau $
-invariant is the Witt class
Casson and Gordon show that
![]() $\tau (K,\chi )$
is independent both of the choice of the 4-manifold
$\tau (K,\chi )$
is independent both of the choice of the 4-manifold
![]() $V_n$
and of the extension
$V_n$
and of the extension
![]() $\psi $
of
$\psi $
of
![]() $\alpha \times \chi $
to
$\alpha \times \chi $
to
![]() $\pi _1(V_n)$
[Reference Casson and Gordon6]. Furthermore, as we shall recall later on,
$\pi _1(V_n)$
[Reference Casson and Gordon6]. Furthermore, as we shall recall later on,
![]() $\tau (K,\chi )$
provides an obstruction to sliceness.
$\tau (K,\chi )$
provides an obstruction to sliceness.
Remark 4.11. Casson and Gordon define their Witt class as an element of
![]() $W(\mathbb {Q}(\xi _m)(t))$
[Reference Casson and Gordon6]. Since the natural map
$W(\mathbb {Q}(\xi _m)(t))$
[Reference Casson and Gordon6]. Since the natural map
![]() $\mathbb {Q}(\xi _m)(t) \to \mathbb {C}(t)$
induces a map on Witt groups, we also obtain a Witt class in
$\mathbb {Q}(\xi _m)(t) \to \mathbb {C}(t)$
induces a map on Witt groups, we also obtain a Witt class in
![]() $W(\mathbb {C}(t))$
. Our reason for working with
$W(\mathbb {C}(t))$
. Our reason for working with
![]() $W(\mathbb {C}(t))$
instead of
$W(\mathbb {C}(t))$
instead of
![]() $W(\mathbb {Q}(\xi _m)(t))$
is the following: the former Witt group is much simpler than the latter, and, in particular, it is more amenable to the machinery we developed in [Reference Borodzik, Conway and Politarczyk3].
$W(\mathbb {Q}(\xi _m)(t))$
is the following: the former Witt group is much simpler than the latter, and, in particular, it is more amenable to the machinery we developed in [Reference Borodzik, Conway and Politarczyk3].
4.4 Casson-Gordon signatures and averaged Blanchfield signatures
In this section, we investigate the relation between the Casson-Gordon invariant
![]() $\tau (K,\chi )$
and the twisted Blanchfield pairing
$\tau (K,\chi )$
and the twisted Blanchfield pairing
![]() $\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(K)$
. In order to make both these invariants more tractable, we use averaged signatures.
$\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(K)$
. In order to make both these invariants more tractable, we use averaged signatures.
Let
![]() $A(t)$
be a matrix over
$A(t)$
be a matrix over
![]() $\mathbb {C}(t)$
. The function
$\mathbb {C}(t)$
. The function
![]() $\operatorname {sign}_\omega (A(t)):=\operatorname {sign}(A(\omega ))$
is a step-function with finitely many discontinuities, and at each discontinuity
$\operatorname {sign}_\omega (A(t)):=\operatorname {sign}(A(\omega ))$
is a step-function with finitely many discontinuities, and at each discontinuity
![]() $\omega $
, we can take the average of the one-sided limits in order to obtain a rational number
$\omega $
, we can take the average of the one-sided limits in order to obtain a rational number
![]() $\operatorname {sign}_\omega ^{\text {av}}(A(t))$
. As explained in [Reference Casson and Gordon6, discussion preceding Theorem 3], one now obtains a well-defined homomorphism
$\operatorname {sign}_\omega ^{\text {av}}(A(t))$
. As explained in [Reference Casson and Gordon6, discussion preceding Theorem 3], one now obtains a well-defined homomorphism
![]() $\operatorname {sign}^{\text {av}}_\omega \colon W(\mathbb {C}(t)) \to \mathbb {Q}$
by setting
$\operatorname {sign}^{\text {av}}_\omega \colon W(\mathbb {C}(t)) \to \mathbb {Q}$
by setting
This map also gives rise to a well-defined map on
![]() $W(\mathbb {C}(t)) \otimes \mathbb {Q}$
. We now apply this discussion to extract signatures from the Casson-Gordon invariant
$W(\mathbb {C}(t)) \otimes \mathbb {Q}$
. We now apply this discussion to extract signatures from the Casson-Gordon invariant
![]() $\tau (K,\chi )$
which is an element of
$\tau (K,\chi )$
which is an element of
![]() $W(\mathbb {C}(t)) \otimes \mathbb {Q}$
.
$W(\mathbb {C}(t)) \otimes \mathbb {Q}$
.
Definition 4.12. The Casson-Gordon signature associated to
![]() $\omega \in S^1$
is
$\omega \in S^1$
is
![]() $\operatorname {sign}_\omega ^{\text {av}}(\tau (K,\chi )) \in \mathbb {Q}$
.
$\operatorname {sign}_\omega ^{\text {av}}(\tau (K,\chi )) \in \mathbb {Q}$
.
Before returning to Blanchfield pairings, let us make Definition 4.12 somewhat more concrete.
Remark 4.13. Suppose
![]() $V_n$
is a
$V_n$
is a
![]() $4$
-manifold whose boundary consists of a disjoint union of r copies of
$4$
-manifold whose boundary consists of a disjoint union of r copies of
![]() $M_n$
and over which
$M_n$
and over which
![]() $\alpha \times \chi $
extends. In other words, we have
$\alpha \times \chi $
extends. In other words, we have
Since
![]() $\operatorname {sign}_\omega ^{\text {av}}$
is a homomorphism, we obtain
$\operatorname {sign}_\omega ^{\text {av}}$
is a homomorphism, we obtain
Clearly, the latter term is simply equal to
![]() $\operatorname {sign}(V_n)$
, the (untwisted) signature of
$\operatorname {sign}(V_n)$
, the (untwisted) signature of
![]() $V_n$
. Consequently, if
$V_n$
. Consequently, if
![]() $A(t)$
represents
$A(t)$
represents
![]() $\lambda _{\mathbb {C}(t)_{\alpha \times \chi },V_n}$
, then we deduce that
$\lambda _{\mathbb {C}(t)_{\alpha \times \chi },V_n}$
, then we deduce that
Note that
![]() $A(1)$
does not represent the standard intersection form
$A(1)$
does not represent the standard intersection form
![]() $\lambda _{\mathbb {Q},V_n}$
. It does, however, represent the twisted intersection form
$\lambda _{\mathbb {Q},V_n}$
. It does, however, represent the twisted intersection form
![]() $\lambda _{\mathbb {C}_{\xi _{m}},V_n}$
which arises from the coefficient system
$\lambda _{\mathbb {C}_{\xi _{m}},V_n}$
which arises from the coefficient system
![]() $\pi _1(V_n) \to \mathbb {Z}_m \to \mathbb {C}$
, where the latter map sends the generator of
$\pi _1(V_n) \to \mathbb {Z}_m \to \mathbb {C}$
, where the latter map sends the generator of
![]() $\mathbb {Z}_m$
to
$\mathbb {Z}_m$
to
![]() $\xi _m=\text {exp}(\frac {2\pi i}{m})$
.
$\xi _m=\text {exp}(\frac {2\pi i}{m})$
.
Returning to Blanchfield pairings, recall from Definition 4.2 that
![]() $\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(K)$
denotes the twisted Blanchfield pairing associated to the representation
$\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(K)$
denotes the twisted Blanchfield pairing associated to the representation
![]() $\alpha (n,\chi ) \colon \pi _1(M_K) \to GL_n({\mathbb {C}}[t^{\pm 1}])$
. Recall furthermore that
$\alpha (n,\chi ) \colon \pi _1(M_K) \to GL_n({\mathbb {C}}[t^{\pm 1}])$
. Recall furthermore that
![]() $\sigma _{K,\alpha (n,\chi )} \colon S^1 \to \mathbb {Z}$
denotes the associated twisted signature function.
$\sigma _{K,\alpha (n,\chi )} \colon S^1 \to \mathbb {Z}$
denotes the associated twisted signature function.
The following theorem relates our Blanchfield signatures to the Casson-Gordon signatures.
Theorem 4.14. Let K be an oriented knot and n be an integer. Let
![]() $\Sigma _n(K)$
be the n-fold cyclic cover of
$\Sigma _n(K)$
be the n-fold cyclic cover of
![]() $S^3$
branched along K and let
$S^3$
branched along K and let
![]() $M_n$
be the n-fold cyclic cover of
$M_n$
be the n-fold cyclic cover of
![]() $M_K$
. If
$M_K$
. If
![]() $\chi \colon H_1(\Sigma _n(K);\mathbb {Z}) \to ~\mathbb {Z}_m$
is a nontrivial character of prime power order m, then the following statements hold:
$\chi \colon H_1(\Sigma _n(K);\mathbb {Z}) \to ~\mathbb {Z}_m$
is a nontrivial character of prime power order m, then the following statements hold:
-
(a) The twisted Blanchfield pairing
 $\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(K)$
is representable.
$\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(K)$
is representable. -
(b) For each
 $\omega $
in
$\omega $
in
 $S^1$
, we have the equality
$S^1$
, we have the equality  $$ \begin{align*}-\sigma^{\text{av}}_{K,\alpha(n,\chi)}(\omega)=\operatorname{sign}_\omega^{\text{av}}(\tau(K,\chi))-\operatorname{sign}_1^{\text{av}}(\tau(K,\chi)).\end{align*} $$
$$ \begin{align*}-\sigma^{\text{av}}_{K,\alpha(n,\chi)}(\omega)=\operatorname{sign}_\omega^{\text{av}}(\tau(K,\chi))-\operatorname{sign}_1^{\text{av}}(\tau(K,\chi)).\end{align*} $$
Before moving toward the proof, we start with a remark and a corollary to Theorem 4.14.
Remark 4.15. Although we stated Theorem 4.14 using the metabelian Blanchfield pairing
![]() $\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(K)$
, the proof will use the Blanchfield pairing of the cover
$\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(K)$
, the proof will use the Blanchfield pairing of the cover
![]() $\operatorname {Bl}_{\alpha \times \chi }(M_n)$
. Indeed, since Corollary 4.6 states that
$\operatorname {Bl}_{\alpha \times \chi }(M_n)$
. Indeed, since Corollary 4.6 states that
![]() $\operatorname {Bl}_{\alpha (n,\chi )}(K)$
and
$\operatorname {Bl}_{\alpha (n,\chi )}(K)$
and
![]() $\operatorname {Bl}_{\alpha \times \chi }(M_n)$
are isometric, one linking form is representable if and only if the other one is, and for every
$\operatorname {Bl}_{\alpha \times \chi }(M_n)$
are isometric, one linking form is representable if and only if the other one is, and for every
![]() $\omega \in S^1$
, the second item of Theorem 4.14 could have been written using the signature function of
$\omega \in S^1$
, the second item of Theorem 4.14 could have been written using the signature function of
![]() $\operatorname {Bl}_{\alpha \times \chi }(M_n)$
, since the following equality holds:
$\operatorname {Bl}_{\alpha \times \chi }(M_n)$
, since the following equality holds:
Since
![]() $\tau (K,\chi )$
is known to provide an obstruction to sliceness [Reference Casson and Gordon6], a similar conclusion holds for
$\tau (K,\chi )$
is known to provide an obstruction to sliceness [Reference Casson and Gordon6], a similar conclusion holds for
![]() $\sigma _{K,\alpha (n,\chi )}$
, thus yielding a second proof of (a variation on) Theorem 4.8. Indeed, recalling that
$\sigma _{K,\alpha (n,\chi )}$
, thus yielding a second proof of (a variation on) Theorem 4.8. Indeed, recalling that
![]() $\lambda _n$
denotes the
$\lambda _n$
denotes the
![]() $\mathbb {Q}/\mathbb {Z}$
-valued linking form on
$\mathbb {Q}/\mathbb {Z}$
-valued linking form on
![]() $H_1(\Sigma _n(K);\mathbb {Z})$
, the following result is an immediate corollary of Theorem 4.14 and [Reference Casson and Gordon6, Theorem 2].
$H_1(\Sigma _n(K);\mathbb {Z})$
, the following result is an immediate corollary of Theorem 4.14 and [Reference Casson and Gordon6, Theorem 2].
Corollary 4.16. If K is slice, then there is a subgroup G of
![]() $H_1(\Sigma _n(K))$
such that
$H_1(\Sigma _n(K))$
such that
![]() $|G|^{2} = |H_{1}(\Sigma _{n}(K))|$
and
$|G|^{2} = |H_{1}(\Sigma _{n}(K))|$
and
![]() $\lambda _n$
vanishes on G, and, for every character
$\lambda _n$
vanishes on G, and, for every character
![]() $\chi $
vanishing on G, the signature function
$\chi $
vanishing on G, the signature function
![]() $ \sigma ^{\text {av}}_{K,\alpha (n,\chi )}(\omega )$
is zero.
$ \sigma ^{\text {av}}_{K,\alpha (n,\chi )}(\omega )$
is zero.
We now move toward the proof of Theorem 4.14. First of all, as we mentioned in Remark 4.15, we can work with the pairing
![]() $\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(M_n)$
instead of
$\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(M_n)$
instead of
![]() $\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(K)$
. Next, as in Subsection 4.3, we choose a smooth
$\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(K)$
. Next, as in Subsection 4.3, we choose a smooth
![]() $4$
-manifold
$4$
-manifold
![]() $V_n$
such that the boundary of
$V_n$
such that the boundary of
![]() $V_n$
consists of r copies of
$V_n$
consists of r copies of
![]() $M_n$
and such that the representation extends. Without loss of generality, we can assume that
$M_n$
and such that the representation extends. Without loss of generality, we can assume that
![]() $\pi _1(V_n)=\mathbb {Z}_m \times \mathbb {Z}$
: indeed, since
$\pi _1(V_n)=\mathbb {Z}_m \times \mathbb {Z}$
: indeed, since
![]() $\mathbb {Z}_m \times \mathbb {Z}$
is finitely normally presented, one can perform finitely many surgeries to obtain the desired fundamental group, while leaving the boundary fixed.
$\mathbb {Z}_m \times \mathbb {Z}$
is finitely normally presented, one can perform finitely many surgeries to obtain the desired fundamental group, while leaving the boundary fixed.
The following lemma collects some algebraic statements which we shall need later on.
Lemma 4.17. The following statements hold:
-
(a) The
 ${\mathbb {C}}[t^{\pm 1}]$
-module
${\mathbb {C}}[t^{\pm 1}]$
-module
 $H_1(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
vanishes.
$H_1(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
vanishes. -
(b) The map
 $\operatorname {\mathrm {ev}} \circ \kappa \colon H^2(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi }) \rightarrow \operatorname {\mathrm {Hom}}_{{\mathbb {C}}[t^{\pm 1}]}(H_2(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi }),{\mathbb {C}}[t^{\pm 1}])^\#$
is an isomorphism.
$\operatorname {\mathrm {ev}} \circ \kappa \colon H^2(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi }) \rightarrow \operatorname {\mathrm {Hom}}_{{\mathbb {C}}[t^{\pm 1}]}(H_2(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi }),{\mathbb {C}}[t^{\pm 1}])^\#$
is an isomorphism. -
(c) The
 ${\mathbb {C}}[t^{\pm 1}]$
-module
${\mathbb {C}}[t^{\pm 1}]$
-module
 $H_2(V_n,\partial V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
is free.
$H_2(V_n,\partial V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
is free. -
(d) The inclusion induced map
 $ H^2(V_n,\partial V_n;\mathbb {C}(t)_{\alpha \times \chi }) \to H^2(V_n;\mathbb {C}(t)_{\alpha \times \chi })$
is an isomorphism.
$ H^2(V_n,\partial V_n;\mathbb {C}(t)_{\alpha \times \chi }) \to H^2(V_n;\mathbb {C}(t)_{\alpha \times \chi })$
is an isomorphism.
Proof. We start by proving (a). Set
![]() $G:=\mathbb {Z}_m \times \mathbb {Z}$
for brevity. Recalling the notation introduced below (4.9), we claim that
$G:=\mathbb {Z}_m \times \mathbb {Z}$
for brevity. Recalling the notation introduced below (4.9), we claim that
![]() ${\mathbb {C}}[t^{\pm 1}]_{G}$
is a projective
${\mathbb {C}}[t^{\pm 1}]_{G}$
is a projective
![]() $\mathbb {C}[G]$
-module. To see this, first note that
$\mathbb {C}[G]$
-module. To see this, first note that
![]() $\mathbb {C}[G] = \mathbb {C}[t^{\pm 1}] \otimes _{\mathbb {C}} \mathbb {C}[\mathbb {Z}_m]$
and
$\mathbb {C}[G] = \mathbb {C}[t^{\pm 1}] \otimes _{\mathbb {C}} \mathbb {C}[\mathbb {Z}_m]$
and
![]() $\mathbb {C}[\mathbb {Z}_m] = \bigoplus _{j = 0}^{m-1}~\mathbb {C}_{\xi _m^j}$
, where
$\mathbb {C}[\mathbb {Z}_m] = \bigoplus _{j = 0}^{m-1}~\mathbb {C}_{\xi _m^j}$
, where
![]() $\mathbb {C}_{\xi _m^j}$
denotes the irreducible complex representation of
$\mathbb {C}_{\xi _m^j}$
denotes the irreducible complex representation of
![]() $\mathbb {Z}_m$
with the action of the cyclic group given by multiplication by the root of unity
$\mathbb {Z}_m$
with the action of the cyclic group given by multiplication by the root of unity
![]() $\xi _m^j$
, for
$\xi _m^j$
, for
![]() $\xi _m = \exp \left (\frac {2 \pi i}{m}\right )$
. Therefore, we have
$\xi _m = \exp \left (\frac {2 \pi i}{m}\right )$
. Therefore, we have
![]() $\mathbb {C}[G] = \bigoplus _{j=0}^{m-1} \mathbb {C}[t^{\pm 1}] \otimes _{\mathbb {C}}~\mathbb {C}_{\xi _m^j}$
and
$\mathbb {C}[G] = \bigoplus _{j=0}^{m-1} \mathbb {C}[t^{\pm 1}] \otimes _{\mathbb {C}}~\mathbb {C}_{\xi _m^j}$
and
![]() ${\mathbb {C}}[t^{\pm 1}]_{G} = \mathbb {C}[t^{\pm 1}] \otimes _{\mathbb {C}}~\mathbb {C}_{\xi _m}$
, concluding the proof of the claim. The claim now implies that
${\mathbb {C}}[t^{\pm 1}]_{G} = \mathbb {C}[t^{\pm 1}] \otimes _{\mathbb {C}}~\mathbb {C}_{\xi _m}$
, concluding the proof of the claim. The claim now implies that
![]() $H_1(V_n; {\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
is a summand of
$H_1(V_n; {\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
is a summand of
![]() $H_1(V_n; \mathbb {C}[G])$
. Since
$H_1(V_n; \mathbb {C}[G])$
. Since
![]() $\pi _1(V_n)=G$
, the corresponding G-cover of
$\pi _1(V_n)=G$
, the corresponding G-cover of
![]() $V_n$
is simply-connected, and thus,
$V_n$
is simply-connected, and thus,
![]() $H_1(V_n;\mathbb {C}[G])$
vanishes. Consequently,
$H_1(V_n;\mathbb {C}[G])$
vanishes. Consequently,
![]() $H_1(V_n; {\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
also vanishes since it is a direct summand of
$H_1(V_n; {\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
also vanishes since it is a direct summand of
![]() $H_1(V_n; \mathbb {C}[G])$
. This concludes the proof of (a).
$H_1(V_n; \mathbb {C}[G])$
. This concludes the proof of (a).
We now prove (b) according to which the evaluation map
is an isomorphism. Since
![]() $H_1(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })=0$
by the first statement and
$H_1(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })=0$
by the first statement and
![]() $H_0(V_n; {\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })=~0$
(recall Lemma 4.1), this follows immediately from the universal coefficient theorem.
$H_0(V_n; {\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })=~0$
(recall Lemma 4.1), this follows immediately from the universal coefficient theorem.
We move on to (c) which asserts that
![]() $H_2(V_n,\partial V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
is a free
$H_2(V_n,\partial V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
is a free
![]() ${\mathbb {C}}[t^{\pm 1}]$
-module. Using Poincaré duality and the second statement, we deduce that
${\mathbb {C}}[t^{\pm 1}]$
-module. Using Poincaré duality and the second statement, we deduce that
![]() $H_2(V_n,\partial V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
is isomorphic to
$H_2(V_n,\partial V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
is isomorphic to
![]() $\operatorname {\mathrm {Hom}}_{{\mathbb {C}}[t^{\pm 1}]}(H_2(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi }),{\mathbb {C}}[t^{\pm 1}])^\#$
which is free because
$\operatorname {\mathrm {Hom}}_{{\mathbb {C}}[t^{\pm 1}]}(H_2(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi }),{\mathbb {C}}[t^{\pm 1}])^\#$
which is free because
![]() ${\mathbb {C}}[t^{\pm 1}]$
is a PID.
${\mathbb {C}}[t^{\pm 1}]$
is a PID.
Finally, we deal with (d); that is we show that the inclusion induced map
![]() $H^2(V_n,\partial V_n;\mathbb {C}(t)_{\alpha \times \chi }) \to H^2(V_n;\mathbb {C}(t)_{\alpha \times \chi })$
is an isomorphism. Since
$H^2(V_n,\partial V_n;\mathbb {C}(t)_{\alpha \times \chi }) \to H^2(V_n;\mathbb {C}(t)_{\alpha \times \chi })$
is an isomorphism. Since
![]() $H_*(M_n;\mathbb {C}(t)_{\alpha \times \chi })$
vanishes by Lemma 4.9 and
$H_*(M_n;\mathbb {C}(t)_{\alpha \times \chi })$
vanishes by Lemma 4.9 and
![]() $\partial V_n$
consists of r disjoint copies of
$\partial V_n$
consists of r disjoint copies of
![]() $M_n$
, we deduce that
$M_n$
, we deduce that
![]() $H_*(\partial V_n;\mathbb {C}(t)_{\alpha \times \chi })$
also vanishes. The long exact sequence of the pair
$H_*(\partial V_n;\mathbb {C}(t)_{\alpha \times \chi })$
also vanishes. The long exact sequence of the pair
![]() $(V_n,\partial V_n)$
implies that
$(V_n,\partial V_n)$
implies that
![]() $H_2(V_n;\mathbb {C}(t)_{\alpha \times \chi }) \rightarrow H_2(V_n,\partial V_n;\mathbb {C}(t)_{\alpha \times \chi })$
is an isomorphism, and the result follows by Poincaré duality. This concludes the proof of (d) and thus the proof of the lemma.
$H_2(V_n;\mathbb {C}(t)_{\alpha \times \chi }) \rightarrow H_2(V_n,\partial V_n;\mathbb {C}(t)_{\alpha \times \chi })$
is an isomorphism, and the result follows by Poincaré duality. This concludes the proof of (d) and thus the proof of the lemma.
Since
![]() ${\mathbb {C}}[t^{\pm 1}]$
is a PID, we can decompose any
${\mathbb {C}}[t^{\pm 1}]$
is a PID, we can decompose any
![]() ${\mathbb {C}}[t^{\pm 1}]$
-module H as the direct sum of its free part
${\mathbb {C}}[t^{\pm 1}]$
-module H as the direct sum of its free part
![]() $FH$
and its torsion part
$FH$
and its torsion part
![]() $TH$
. While
$TH$
. While
![]() $FH$
is typically defined as
$FH$
is typically defined as
![]() $H/TH$
, here it is convenient to think of
$H/TH$
, here it is convenient to think of
![]() $FH$
as a submodule of H such that
$FH$
as a submodule of H such that
![]() $H \cong FH \oplus TH$
. While such a submodule is not unique, different choices will not affect the remainder of the proof. In particular, it follows that
$H \cong FH \oplus TH$
. While such a submodule is not unique, different choices will not affect the remainder of the proof. In particular, it follows that
Consequently, point (b) of Lemma 4.17 provides the following well-defined isomorphism:
Composing the inclusion
![]() $FH_2(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi }) \to H_2(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
with the inclusion induced map
$FH_2(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi }) \to H_2(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
with the inclusion induced map
![]() $H_2(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi }) \to H_2(V_n,\partial V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
gives rise to a well-defined map
$H_2(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi }) \to H_2(V_n,\partial V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
gives rise to a well-defined map
Combining these remarks, there is a well-defined intersection form
Here, note that the choice of the submodule of
![]() $FH$
does not affect the isometry type of
$FH$
does not affect the isometry type of
![]() $\lambda _{{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi },V_n}$
.
$\lambda _{{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi },V_n}$
.
Next, we describe the Blanchfield
![]() $\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(\partial V_n)$
on
$\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(\partial V_n)$
on
![]() $H_1(\partial V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
. As
$H_1(\partial V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
. As
![]() $\partial V_n$
consists of r copies of
$\partial V_n$
consists of r copies of
![]() $M_n$
, we deduce that
$M_n$
, we deduce that
![]() $H_1(\partial V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
is isomorphic to the direct sum of r copies of
$H_1(\partial V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
is isomorphic to the direct sum of r copies of
![]() $H_1(M_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
. Since the latter
$H_1(M_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
. Since the latter
![]() ${\mathbb {C}}[t^{\pm 1}]$
-module is torsion, so is the former. We deduce that
${\mathbb {C}}[t^{\pm 1}]$
-module is torsion, so is the former. We deduce that
![]() $ \operatorname {\mathrm {Bl}}_{\alpha \times \chi }(\partial V_n)$
decomposes as the direct sum
$ \operatorname {\mathrm {Bl}}_{\alpha \times \chi }(\partial V_n)$
decomposes as the direct sum
![]() $\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(M_n) \oplus \cdots \oplus \operatorname {\mathrm {Bl}}_{\alpha \times \chi }(M_n)$
, where there are r direct summands.
$\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(M_n) \oplus \cdots \oplus \operatorname {\mathrm {Bl}}_{\alpha \times \chi }(M_n)$
, where there are r direct summands.
The proof of the next result is postponed until the end of the proof of Theorem 4.14.
Proposition 4.18. Any matrix
![]() $A(t)$
representing
$A(t)$
representing
![]() $\lambda _{{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi },V_n}$
also represents
$\lambda _{{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi },V_n}$
also represents
![]() $\lambda _{\mathbb {C}(t)_{\alpha \times \chi },V_n}$
and
$\lambda _{\mathbb {C}(t)_{\alpha \times \chi },V_n}$
and
![]() $-\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(\partial V_n)$
.
$-\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(\partial V_n)$
.
Proof of Theorem 4.14 assuming Proposition 4.18
We start by proving the second statement – namely, the equality of signatures. Let
![]() $A(t)$
be a matrix representing
$A(t)$
be a matrix representing
![]() $\lambda _{{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi },V_n}$
. Since
$\lambda _{{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi },V_n}$
. Since
![]() $A(t)$
represents the twisted intersection form
$A(t)$
represents the twisted intersection form
![]() $\lambda _{\mathbb {C}(t)_{\alpha \times \chi },V_n}$
, the definition of the Casson-Gordon signature and Remark 4.13 imply that
$\lambda _{\mathbb {C}(t)_{\alpha \times \chi },V_n}$
, the definition of the Casson-Gordon signature and Remark 4.13 imply that
Since Proposition 4.18 tells us that
![]() $A(t)$
also represents
$A(t)$
also represents
![]() $-\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(\partial V_n)$
, item (S-5) of Proposition 1.6 implies that
$-\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(\partial V_n)$
, item (S-5) of Proposition 1.6 implies that
![]() $-\operatorname {sign}_\omega ^{\text {av}}(\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(\partial V_n))=\operatorname {sign}^{\text {av}}_\omega (A(t))-\operatorname {sign}^{\text {av}}_1(A(t))$
. However, since
$-\operatorname {sign}_\omega ^{\text {av}}(\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(\partial V_n))=\operatorname {sign}^{\text {av}}_\omega (A(t))-\operatorname {sign}^{\text {av}}_1(A(t))$
. However, since
![]() $\partial V_n$
consists of r disjoint copies of
$\partial V_n$
consists of r disjoint copies of
![]() $M_n$
, we observed previously that
$M_n$
, we observed previously that
![]() $ \operatorname {\mathrm {Bl}}_{\alpha \times \chi }(\partial V_n)=\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(M_n) \oplus \ldots \oplus \operatorname {\mathrm {Bl}}_{\alpha \times \chi }(M_n)$
and, consequently,
$ \operatorname {\mathrm {Bl}}_{\alpha \times \chi }(\partial V_n)=\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(M_n) \oplus \ldots \oplus \operatorname {\mathrm {Bl}}_{\alpha \times \chi }(M_n)$
and, consequently,
![]() $\operatorname {sign}_\omega ^{\text {av}}(\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(\partial V_n))=r \cdot \operatorname {sign}_\omega ^{\text {av}}(\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(M_n))$
. Combining these two observations, we obtain the following equality:
$\operatorname {sign}_\omega ^{\text {av}}(\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(\partial V_n))=r \cdot \operatorname {sign}_\omega ^{\text {av}}(\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(M_n))$
. Combining these two observations, we obtain the following equality:
Finally, adding and subtracting a
![]() $\text {sign}(V_n)$
term in (4.13) and combining the result with (4.12), we can conclude the proof of the first assertion:
$\text {sign}(V_n)$
term in (4.13) and combining the result with (4.12), we can conclude the proof of the first assertion:
 $$ \begin{align*} -\operatorname{sign}^{\text{av}}_\omega(\operatorname{\mathrm{Bl}}_{\alpha \times \chi}( M_n)) &=\frac{1}{r}\left(\operatorname{sign}^{\text{av}}_\omega(A(t))-\operatorname{sign}(V_n)\right)-\frac{1}{r}\left(\operatorname{sign}^{\text{av}}_1(A(t))-\operatorname{sign}(V_n) \right) \\ &=\operatorname{sign}_\omega^{\text{av}}(\tau(K,\chi))-\operatorname{sign}_1^{\text{av}}(\tau(K,\chi)). \end{align*} $$
$$ \begin{align*} -\operatorname{sign}^{\text{av}}_\omega(\operatorname{\mathrm{Bl}}_{\alpha \times \chi}( M_n)) &=\frac{1}{r}\left(\operatorname{sign}^{\text{av}}_\omega(A(t))-\operatorname{sign}(V_n)\right)-\frac{1}{r}\left(\operatorname{sign}^{\text{av}}_1(A(t))-\operatorname{sign}(V_n) \right) \\ &=\operatorname{sign}_\omega^{\text{av}}(\tau(K,\chi))-\operatorname{sign}_1^{\text{av}}(\tau(K,\chi)). \end{align*} $$
It remains to prove the first statement – namely, that the twisted Blanchfield pairing
![]() $\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(M_n)$
is representable. In the previous paragraph, we showed that
$\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(M_n)$
is representable. In the previous paragraph, we showed that
![]() $ \operatorname {\mathrm {Bl}}_{\alpha \times \chi }(\partial V_n)=\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(M_n) \oplus \ldots \oplus \operatorname {\mathrm {Bl}}_{\alpha \times \chi }(M_n)$
. Since we know from Proposition 4.18 that
$ \operatorname {\mathrm {Bl}}_{\alpha \times \chi }(\partial V_n)=\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(M_n) \oplus \ldots \oplus \operatorname {\mathrm {Bl}}_{\alpha \times \chi }(M_n)$
. Since we know from Proposition 4.18 that
![]() $\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(\partial V_n)$
is representable,
$\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(\partial V_n)$
is representable,
![]() $\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(M_n) $
is itself representable (
$\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(M_n) $
is itself representable (
![]() $\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(\partial V_n)$
satisfies the signature condition of item (S-6) of Proposition 1.6, and thus, so does
$\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(\partial V_n)$
satisfies the signature condition of item (S-6) of Proposition 1.6, and thus, so does
![]() $\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(M_n)$
), and so the theorem is proved.
$\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(M_n)$
), and so the theorem is proved.
We now prove Proposition 4.18; the strategy follows very closely [Reference Conway, Friedl and Toffoli13, Section 5.2] which itself is based on the proof of [Reference Borodzik and Friedl4, Theorem 2.6].
Proof of Proposition 4.18
Consider the following diagram in which all homomorphisms are understood to be homomorphisms of
![]() ${\mathbb {C}}[t^{\pm 1}]$
-modules:
${\mathbb {C}}[t^{\pm 1}]$
-modules:

To make the diagram more concise, we have used the following shorthands:
-
•
 $\Lambda ={\mathbb {C}}[t^{\pm 1}]$
;
$\Lambda ={\mathbb {C}}[t^{\pm 1}]$
; -
•
 $FH_2=FH_2(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
;
$FH_2=FH_2(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
; -
•
 $H=H_2(V_n,\partial V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
;
$H=H_2(V_n,\partial V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
; -
•
 $\Omega =\mathbb {C}(t)$
.
$\Omega =\mathbb {C}(t)$
.
The top horizontal line of (4.14) is exact thanks to the long exact sequence of the pair
![]() $(V_n,\partial V_n)$
together with Lemma 4.17: exactness at the rightmost end is guaranteed by the first point of Lemma 4.17, while exactness at the middle follows from the third point. In more details, since
$(V_n,\partial V_n)$
together with Lemma 4.17: exactness at the rightmost end is guaranteed by the first point of Lemma 4.17, while exactness at the middle follows from the third point. In more details, since
![]() $H:=H_2(V_n,\partial V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
is free, the image of
$H:=H_2(V_n,\partial V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
is free, the image of
![]() $H_2(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
in H is equal to the image of
$H_2(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
in H is equal to the image of
![]() $FH_2(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
in H.
$FH_2(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
in H.
The commutativity of the top middle square is a consequence of the definition of the Poincaré duality isomorphism. All the squares involving evaluation maps clearly commute, while the upper left (resp. right) square commutes by definition of the intersection (resp. Blanchfield) pairing. Finally, the middle rectangle anti-commutes thanks to [Reference Conway, Friedl and Toffoli13, Lemma 5.4]; see [Reference Conway12, Appendix A] for a proof.
Inspired by (4.14), we define a pairing
![]() $\theta $
on
$\theta $
on
![]() $H_2(V_n,\partial V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
by the composition
$H_2(V_n,\partial V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
by the composition
 $$ \begin{align*} H_2(V_n,\partial V_n;{\mathbb{C}}[t^{\pm 1}]_{\alpha \times \chi}) &\xrightarrow{\operatorname{PD}} H^2(V_n;{\mathbb{C}}[t^{\pm 1}]_{\alpha \times \chi}) \rightarrow H^2(V_n;\mathbb{C}(t)_{\alpha\times \chi}) \cong H^2(V_n,\partial V_n;\mathbb{C}(t)_{\alpha\times \chi}) \\ &\rightarrow \operatorname{\mathrm{Hom}}_{{\mathbb{C}}[t^{\pm 1}]}(H_2(V_n,\partial V_n;{\mathbb{C}}[t^{\pm 1}]_{\alpha \times \chi}),\mathbb{C}(t))^\#, \end{align*} $$
$$ \begin{align*} H_2(V_n,\partial V_n;{\mathbb{C}}[t^{\pm 1}]_{\alpha \times \chi}) &\xrightarrow{\operatorname{PD}} H^2(V_n;{\mathbb{C}}[t^{\pm 1}]_{\alpha \times \chi}) \rightarrow H^2(V_n;\mathbb{C}(t)_{\alpha\times \chi}) \cong H^2(V_n,\partial V_n;\mathbb{C}(t)_{\alpha\times \chi}) \\ &\rightarrow \operatorname{\mathrm{Hom}}_{{\mathbb{C}}[t^{\pm 1}]}(H_2(V_n,\partial V_n;{\mathbb{C}}[t^{\pm 1}]_{\alpha \times \chi}),\mathbb{C}(t))^\#, \end{align*} $$
where the third map is an isomorphism thanks to the fourth point of Lemma 4.17. The commutativity of the diagram in equation (4.14) immediately implies the commutativity of

We now pick bases in order to obtain matrices for the intersection form. Namely, choose any basis
![]() $\mathcal {C}$
of
$\mathcal {C}$
of
![]() $FH_2(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
and endow
$FH_2(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
and endow
![]() $\operatorname {\mathrm {Hom}}_{{\mathbb {C}}[t^{\pm 1}]}(FH_2(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi }),{\mathbb {C}}[t^{\pm 1}])^\#$
with the corresponding dual basis
$\operatorname {\mathrm {Hom}}_{{\mathbb {C}}[t^{\pm 1}]}(FH_2(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi }),{\mathbb {C}}[t^{\pm 1}])^\#$
with the corresponding dual basis
![]() $\mathcal {C}^*$
. Let
$\mathcal {C}^*$
. Let
![]() $A(t)$
denote the matrix of the
$A(t)$
denote the matrix of the
![]() ${\mathbb {C}}[t^{\pm 1}]$
-intersection form
${\mathbb {C}}[t^{\pm 1}]$
-intersection form
![]() $\lambda _{{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi },V_n}$
with respect to these bases.
$\lambda _{{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi },V_n}$
with respect to these bases.
Next, we use
![]() $\mathcal {C}$
and
$\mathcal {C}$
and
![]() $\mathcal {C}^*$
to base
$\mathcal {C}^*$
to base
![]() $H_2(V_n;\mathbb {C}(t)_{\alpha \times \chi })$
and
$H_2(V_n;\mathbb {C}(t)_{\alpha \times \chi })$
and
![]() $\operatorname {\mathrm {Hom}}_{{\mathbb {C}}[t^{\pm 1}]}(H_2(V_n;\mathbb {C}(t)_{\alpha \times \chi }),\mathbb {C}(t))^\#$
. In other words, as claimed in the first part of Proposition 4.18, there are bases with respect to which both
$\operatorname {\mathrm {Hom}}_{{\mathbb {C}}[t^{\pm 1}]}(H_2(V_n;\mathbb {C}(t)_{\alpha \times \chi }),\mathbb {C}(t))^\#$
. In other words, as claimed in the first part of Proposition 4.18, there are bases with respect to which both
![]() $\lambda _{\mathbb {C}(t)_{\alpha \times \chi },V_n}$
and
$\lambda _{\mathbb {C}(t)_{\alpha \times \chi },V_n}$
and
![]() $\lambda _{{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi },V_n}$
are represented by
$\lambda _{{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi },V_n}$
are represented by
![]() $A(t)$
. Therefore, to conclude the proof, it only remains to show that
$A(t)$
. Therefore, to conclude the proof, it only remains to show that
![]() $A(t)$
also represents the Blanchfield pairing on
$A(t)$
also represents the Blanchfield pairing on
![]() $\partial V_n$
.
$\partial V_n$
.
With this aim in mind, we start by providing a basis for
![]() $H_2(V_n,\partial V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
(which is free by Lemma 4.17(b)). This will allow us to represent the inclusion induced map
$H_2(V_n,\partial V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
(which is free by Lemma 4.17(b)). This will allow us to represent the inclusion induced map
![]() $FH_2(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi }) \to H_2(V_n,\partial V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
by a matrix. First, consider the following commutative diagram of
$FH_2(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi }) \to H_2(V_n,\partial V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
by a matrix. First, consider the following commutative diagram of
![]() ${\mathbb {C}}[t^{\pm 1}]$
-homomorphisms:
${\mathbb {C}}[t^{\pm 1}]$
-homomorphisms:

Here, the bottom-right map is an isomorphism thanks to the second point of Lemma 4.17. We now equip
![]() $H_2(V_n,\partial V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
with the basis induced from
$H_2(V_n,\partial V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
with the basis induced from
![]() $\mathcal {C}^*$
and two isomorphisms in the right column of diagram in (4.16). Arguing as in [Reference Conway, Friedl and Toffoli13, Claim in Section 5.3], elementary linear algebra shows that with respect to these bases, the map
$\mathcal {C}^*$
and two isomorphisms in the right column of diagram in (4.16). Arguing as in [Reference Conway, Friedl and Toffoli13, Claim in Section 5.3], elementary linear algebra shows that with respect to these bases, the map
![]() $FH_2(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi }) \to H_2(V_n,\partial V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
is represented by the matrix
$FH_2(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi }) \to H_2(V_n,\partial V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
is represented by the matrix
![]() $A(t)^T$
. Rewriting the commutative diagram of equation (4.15) in terms of these bases, we obtain
$A(t)^T$
. Rewriting the commutative diagram of equation (4.15) in terms of these bases, we obtain

Here, the middle horizontal map is determined by the top horizontal map, the vertical maps and the commutativity. Since
![]() $H_1(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
vanishes by the first point of Lemma 4.17, we deduce that the Blanchfield pairing on
$H_1(V_n;{\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
vanishes by the first point of Lemma 4.17, we deduce that the Blanchfield pairing on
![]() $H_1(\partial V_n; {\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
is represented by
$H_1(\partial V_n; {\mathbb {C}}[t^{\pm 1}]_{\alpha \times \chi })$
is represented by
![]() $-A(t)$
. This concludes the proof of Proposition 4.18 and thus the proof of Theorem 4.14.
$-A(t)$
. This concludes the proof of Proposition 4.18 and thus the proof of Theorem 4.14.
4.5 Satellite formulas for metabelian Blanchfield forms
Given two knots
![]() $K,P$
and an unknotted curve
$K,P$
and an unknotted curve
![]() $\eta $
in the complement of P, we use
$\eta $
in the complement of P, we use
![]() $P(K,\eta )$
to denote the resulting satellite knot. As described in Subsection 4.1, for a character
$P(K,\eta )$
to denote the resulting satellite knot. As described in Subsection 4.1, for a character
![]() $\chi \colon H_1(\Sigma _n(P(K,\eta ));\mathbb {Z}) \to \mathbb {Z}_{m}$
, there is an associated metabelian representation
$\chi \colon H_1(\Sigma _n(P(K,\eta ));\mathbb {Z}) \to \mathbb {Z}_{m}$
, there is an associated metabelian representation
![]() $\alpha (n,\chi ) \colon \pi _1(M_{P(K,\eta )}) \to GL_n(\mathbb {C}[t^{\pm 1}])$
. The goal of this subsection is to apply the satellite formula of Theorem 3.11 to
$\alpha (n,\chi ) \colon \pi _1(M_{P(K,\eta )}) \to GL_n(\mathbb {C}[t^{\pm 1}])$
. The goal of this subsection is to apply the satellite formula of Theorem 3.11 to
![]() $\alpha (n,\chi )$
. On the level of signatures, the result is reminiscent of Litherland’s description of the behavior of the Casson-Gordon invariants of satellite knots [Reference Litherland38, Theorem 2], but differs in the winding number zero case.
$\alpha (n,\chi )$
. On the level of signatures, the result is reminiscent of Litherland’s description of the behavior of the Casson-Gordon invariants of satellite knots [Reference Litherland38, Theorem 2], but differs in the winding number zero case.
If the representation
![]() $\alpha (n,\chi )$
is
$\alpha (n,\chi )$
is
![]() $\eta $
-regular, then it gives rise to representations
$\eta $
-regular, then it gives rise to representations
![]() $\alpha (n,\chi )_P$
on
$\alpha (n,\chi )_P$
on
![]() $\pi _1(M_P)$
and
$\pi _1(M_P)$
and
![]() $\alpha (n,\chi )_K$
on
$\alpha (n,\chi )_K$
on
![]() $\pi _1(M_K)$
. The representation
$\pi _1(M_K)$
. The representation
![]() $\alpha (n,\chi )_P$
can be shown to agree with
$\alpha (n,\chi )_P$
can be shown to agree with
![]() $\alpha (n,\chi _P)$
, where
$\alpha (n,\chi _P)$
, where
![]() $\chi _P$
is the character induced by
$\chi _P$
is the character induced by
![]() $\chi $
on
$\chi $
on
![]() $H_1(\Sigma _n(P);\mathbb {Z})$
; see [Reference Litherland38, Section 4]. In order to state and prove the metabelian satellite formula, we need to better understand
$H_1(\Sigma _n(P);\mathbb {Z})$
; see [Reference Litherland38, Section 4]. In order to state and prove the metabelian satellite formula, we need to better understand
![]() $\alpha (n,\chi )_K$
.
$\alpha (n,\chi )_K$
.
The composition
![]() $H_1(M_K;\mathbb {Z}) \cong H_1(X_K;\mathbb {Z}) \to H_1(M_{P(K,\eta )};\mathbb {Z}) \cong \mathbb {Z}$
is given by multiplication by
$H_1(M_K;\mathbb {Z}) \cong H_1(X_K;\mathbb {Z}) \to H_1(M_{P(K,\eta )};\mathbb {Z}) \cong \mathbb {Z}$
is given by multiplication by
![]() $w=\ell k(\eta ,P)$
. Thus, the corresponding cover of
$w=\ell k(\eta ,P)$
. Thus, the corresponding cover of
![]() $M_K$
is disconnected and has
$M_K$
is disconnected and has
![]() $|w|$
components (if
$|w|$
components (if
![]() $w=0$
, then the covering is trivial, and so we temporarily disregard this case). Using
$w=0$
, then the covering is trivial, and so we temporarily disregard this case). Using
![]() $t_Q$
(resp.
$t_Q$
(resp.
![]() $t_K$
) to denote the generator of the deck transformation group of the infinite cyclic cover of
$t_K$
) to denote the generator of the deck transformation group of the infinite cyclic cover of
![]() $M_{P(K,\eta )}$
(resp.
$M_{P(K,\eta )}$
(resp.
![]() $M_K$
), we note that
$M_K$
), we note that
![]() $t_Q^w=t_K$
and consider the following inclusion induced map:
$t_Q^w=t_K$
and consider the following inclusion induced map:
 $$ \begin{align} \iota_* \colon \bigoplus_{i=1}^{|w|} t_Q^{i-1} H_1(M_K;\mathbb{Z}[t_K^{\pm 1}]) \cong H_1(M_K;\mathbb{Z}[t_Q^{\pm 1}]) \to H_1(M_{P(K,\eta)};\mathbb{Z}[t_Q^{\pm 1}]). \end{align} $$
$$ \begin{align} \iota_* \colon \bigoplus_{i=1}^{|w|} t_Q^{i-1} H_1(M_K;\mathbb{Z}[t_K^{\pm 1}]) \cong H_1(M_K;\mathbb{Z}[t_Q^{\pm 1}]) \to H_1(M_{P(K,\eta)};\mathbb{Z}[t_Q^{\pm 1}]). \end{align} $$
In order to obtain maps on the branched covers, we shall quotient both sides of (4.17) by
![]() $t_{Q}^{n}-1$
. On the right-hand side, the result is
$t_{Q}^{n}-1$
. On the right-hand side, the result is
![]() $H_1(\Sigma _n(P(K,\eta ));\mathbb {Z})$
, and so we focus on the left-hand side. Write
$H_1(\Sigma _n(P(K,\eta ));\mathbb {Z})$
, and so we focus on the left-hand side. Write
![]() $h:=\gcd (w,n)$
and observe that
$h:=\gcd (w,n)$
and observe that
![]() $t_{K}^{n/h}=t_Q^{wn/h}=t_Q^{\operatorname {lcm}(n,w)}=1 \pmod {t_{Q}^{n}-1}$
. Thus, the map
$t_{K}^{n/h}=t_Q^{wn/h}=t_Q^{\operatorname {lcm}(n,w)}=1 \pmod {t_{Q}^{n}-1}$
. Thus, the map
![]() $i_*$
of (4.17) descends to a map
$i_*$
of (4.17) descends to a map
 $$ \begin{align*}\bigoplus_{i=1}^{h} t_Q^{i-1} H_1(\Sigma_{n/h}(K);\mathbb{Z}) \to H_1(\Sigma_n(P(K,\eta));\mathbb{Z}),\end{align*} $$
$$ \begin{align*}\bigoplus_{i=1}^{h} t_Q^{i-1} H_1(\Sigma_{n/h}(K);\mathbb{Z}) \to H_1(\Sigma_n(P(K,\eta));\mathbb{Z}),\end{align*} $$
where we are thinking of
![]() $H_{1}(\Sigma _{n/h}(K);\mathbb {Z})$
as
$H_{1}(\Sigma _{n/h}(K);\mathbb {Z})$
as
![]() $H_1(M_K;\mathbb {Z}[t_K^{\pm 1}])/(t_K^{n/h}-1)$
. From now on, we fix a copy of
$H_1(M_K;\mathbb {Z}[t_K^{\pm 1}])/(t_K^{n/h}-1)$
. From now on, we fix a copy of
![]() $H_1(\Sigma _{n/h}(K);\mathbb {Z}) $
in this direct sum once and for all. Using this copy, we obtain a map
$H_1(\Sigma _{n/h}(K);\mathbb {Z}) $
in this direct sum once and for all. Using this copy, we obtain a map
Since
![]() $t_K^{n/h}-1=0$
mod
$t_K^{n/h}-1=0$
mod
![]() $t_Q^n-1$
, the character
$t_Q^n-1$
, the character
![]() $\chi $
descends to a character on each
$\chi $
descends to a character on each
![]() $t_Q^{i-1} H_1(\Sigma _{n/h}(K);\mathbb {Z})$
. Thus, for
$t_Q^{i-1} H_1(\Sigma _{n/h}(K);\mathbb {Z})$
. Thus, for
![]() $i=1,\ldots ,h$
, the character
$i=1,\ldots ,h$
, the character
![]() $\chi $
gives rise to the following characters:
$\chi $
gives rise to the following characters:
 $$ \begin{align*} \chi_{i} \colon H_{1}(\Sigma_{n/h}(K);\mathbb{Z}) &\to \mathbb{Z}_m \\ v &\mapsto \chi(t_{Q}^{i-1} \iota_n(v)). \end{align*} $$
$$ \begin{align*} \chi_{i} \colon H_{1}(\Sigma_{n/h}(K);\mathbb{Z}) &\to \mathbb{Z}_m \\ v &\mapsto \chi(t_{Q}^{i-1} \iota_n(v)). \end{align*} $$
We use
![]() $\mu _Q$
(resp.
$\mu _Q$
(resp.
![]() $\mu _K$
) to denote the meridian of
$\mu _K$
) to denote the meridian of
![]() $M_{P(K,\eta )}$
(resp.
$M_{P(K,\eta )}$
(resp.
![]() $M_K$
). Then, just as in Subsection 4.1, we consider the following composition of canonical projections:
$M_K$
). Then, just as in Subsection 4.1, we consider the following composition of canonical projections:
Observe that
![]() $\mu _Q^{-w}\eta $
has trivial abelianization and therefore belongs to
$\mu _Q^{-w}\eta $
has trivial abelianization and therefore belongs to
![]() $\pi _{1}(M_{P(K,\eta )})^{(1)}$
. Finally, given
$\pi _{1}(M_{P(K,\eta )})^{(1)}$
. Finally, given
![]() $\omega \in S^1$
and
$\omega \in S^1$
and
![]() $m \geq 0$
, we write
$m \geq 0$
, we write
![]() $\operatorname {\mathrm {Bl}}(J)(\omega t^m)$
for the twisted Blanchfield pairing associated to the representation
$\operatorname {\mathrm {Bl}}(J)(\omega t^m)$
for the twisted Blanchfield pairing associated to the representation
![]() $\pi _1(M_J) \to GL_1({\mathbb {C}}[t^{\pm 1}]), \gamma \mapsto \omega t^{m \ell k(\gamma ,\mu _J)}$
. When
$\pi _1(M_J) \to GL_1({\mathbb {C}}[t^{\pm 1}]), \gamma \mapsto \omega t^{m \ell k(\gamma ,\mu _J)}$
. When
![]() $m=1$
and
$m=1$
and
![]() $\omega =1$
, this reduces to the usual Blanchfield form
$\omega =1$
, this reduces to the usual Blanchfield form
![]() $\operatorname {\mathrm {Bl}}(J)$
. The main result of this section is the following.
$\operatorname {\mathrm {Bl}}(J)$
. The main result of this section is the following.
Theorem 4.19. Let
![]() $K,P$
be two knots in
$K,P$
be two knots in
![]() $S^{3}$
, let
$S^{3}$
, let
![]() $\eta $
be an unknotted curve in the complement of P with meridian
$\eta $
be an unknotted curve in the complement of P with meridian
![]() $\mu _\eta $
, let
$\mu _\eta $
, let
![]() $w=\operatorname {\mathrm {lk}}(\eta ,P)$
, let
$w=\operatorname {\mathrm {lk}}(\eta ,P)$
, let
![]() $n>1$
and set
$n>1$
and set
![]() $h = \gcd (n,w)$
.
$h = \gcd (n,w)$
.
-
• If
 $w\neq 0$
, then for any character
$w\neq 0$
, then for any character
 $\chi \colon H_1(\Sigma _n(P(K,\eta ));\mathbb {Z}) \to \mathbb {Z}_{m}$
of prime power order, the metabelian representation
$\chi \colon H_1(\Sigma _n(P(K,\eta ));\mathbb {Z}) \to \mathbb {Z}_{m}$
of prime power order, the metabelian representation
 $\alpha (n,\chi )$
is
$\alpha (n,\chi )$
is
 $\eta $
-regular. Moreover,
$\eta $
-regular. Moreover,-
(1) if w is divisible by n, then there exists an isometry of linking forms
 $$\begin{align*}\operatorname{\mathrm{Bl}}_{\alpha(n,\chi)}(P(K,\eta)) \cong \operatorname{\mathrm{Bl}}_{\alpha(n,\chi_P)}(P) \oplus \bigoplus_{i=1}^{n} \operatorname{\mathrm{Bl}}(K)(\xi_{m}^{\chi_{i}(q_Q(\mu_Q^{-w}\eta))}t^{w/n});\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Bl}}_{\alpha(n,\chi)}(P(K,\eta)) \cong \operatorname{\mathrm{Bl}}_{\alpha(n,\chi_P)}(P) \oplus \bigoplus_{i=1}^{n} \operatorname{\mathrm{Bl}}(K)(\xi_{m}^{\chi_{i}(q_Q(\mu_Q^{-w}\eta))}t^{w/n});\end{align*}$$
-
(2) if w is not divisible by n, then
 $\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(P(K,\eta ))$
is Witt equivalent to
$\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(P(K,\eta ))$
is Witt equivalent to  $$\begin{align*}\operatorname{\mathrm{Bl}}_{\alpha(n,\chi_{P})} (P)\oplus \bigoplus_{i=1}^{h} \operatorname{\mathrm{Bl}}_{\alpha(n/h,\chi_{i})}(K)(\xi_{m}^{\chi_{i}(q_Q(\mu_Q^{-w}\eta))}t^{w/h}).\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Bl}}_{\alpha(n,\chi_{P})} (P)\oplus \bigoplus_{i=1}^{h} \operatorname{\mathrm{Bl}}_{\alpha(n/h,\chi_{i})}(K)(\xi_{m}^{\chi_{i}(q_Q(\mu_Q^{-w}\eta))}t^{w/h}).\end{align*}$$
-
-
• If
 $w=0$
, then the representation
$w=0$
, then the representation
 $\alpha (n,\chi )$
is
$\alpha (n,\chi )$
is
 $\eta $
-regular if and only if
$\eta $
-regular if and only if
 $\chi _i(q_Q(\mu _K^{-w}\eta )) \neq 0$
for each
$\chi _i(q_Q(\mu _K^{-w}\eta )) \neq 0$
for each
 $i=1,\ldots ,n$
. In this case, there exists an isometry of linking forms
$i=1,\ldots ,n$
. In this case, there exists an isometry of linking forms  $$\begin{align*}\operatorname{\mathrm{Bl}}_{\alpha(n,\chi)}(P(K,\eta)) \cong \operatorname{\mathrm{Bl}}_{\alpha(n,\chi_P)}(P).\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Bl}}_{\alpha(n,\chi)}(P(K,\eta)) \cong \operatorname{\mathrm{Bl}}_{\alpha(n,\chi_P)}(P).\end{align*}$$
On the level of averaged signatures, Theorem 4.19 is reminiscent of Litherland’s description of the behavior of the Casson-Gordon invariants of satellite knots [Reference Litherland38, Theorem 2].
Remark 4.20. Taking averaged signatures in Theorem 4.19 (and applying item (S-3) of Proposition 1.6), we see that when the winding number w is non-zero, our metabelian signatures behave in the same way as the Casson-Gordon signatures do [Reference Litherland38, Theorem 2]. However, when
![]() $w=0$
, the behaviors differ: namely, we obtain
$w=0$
, the behaviors differ: namely, we obtain
![]() $\sigma ^{\text {av}}_{P(K,\eta ),\alpha (n,\chi )}(\omega )=\sigma ^{\text {av}}_{P,\alpha (n,\chi _P)}(\omega )$
; the Levine-Tristram signatures of the companion knot do not contribute, contrarily do Litherland’s formula for
$\sigma ^{\text {av}}_{P(K,\eta ),\alpha (n,\chi )}(\omega )=\sigma ^{\text {av}}_{P,\alpha (n,\chi _P)}(\omega )$
; the Levine-Tristram signatures of the companion knot do not contribute, contrarily do Litherland’s formula for
![]() $\operatorname {sign}^{av}_{\omega } \tau (P(K,\eta ),\chi )$
. This can also be seen by combining Theorem 4.14 with [Reference Litherland38, Corollary 2].
$\operatorname {sign}^{av}_{\omega } \tau (P(K,\eta ),\chi )$
. This can also be seen by combining Theorem 4.14 with [Reference Litherland38, Corollary 2].
We explain why, in the winding number zero case, it should not come as a surprise that Litherland’s formula for
![]() $\tau (P(K,\eta ),\chi )$
has a contribution from the companion knot K, while our formula for
$\tau (P(K,\eta ),\chi )$
has a contribution from the companion knot K, while our formula for
![]() $\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(P(K,\eta ))$
does not. Litherland’s result [Reference Litherland38, Corollary 2] implies that the difference
$\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(P(K,\eta ))$
does not. Litherland’s result [Reference Litherland38, Corollary 2] implies that the difference
![]() $f(\omega ) = \operatorname {sign}^{av}_{\omega } \tau (P(K,\eta ),\chi ) - \operatorname {sign}^{av}_{\omega } \tau (P,\chi _P)$
is a constant function of
$f(\omega ) = \operatorname {sign}^{av}_{\omega } \tau (P(K,\eta ),\chi ) - \operatorname {sign}^{av}_{\omega } \tau (P,\chi _P)$
is a constant function of
![]() $\omega \in S^{1}$
. In fact, the value of f is expressible in terms of a value of the Levine-Tristram signature of the companion knot K. In particular, this shows that K does not contribute any signature jumps to
$\omega \in S^{1}$
. In fact, the value of f is expressible in terms of a value of the Levine-Tristram signature of the companion knot K. In particular, this shows that K does not contribute any signature jumps to
![]() $\operatorname {sign}_{\omega }^{av}(\tau (P(K,\eta ),\chi ))$
. Since the Witt class of
$\operatorname {sign}_{\omega }^{av}(\tau (P(K,\eta ),\chi ))$
. Since the Witt class of
![]() $\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(P(K,\eta ))$
precisely captures these signature jumps, this gives another explanation of why a contribution of K should not be expected in our formula.
$\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(P(K,\eta ))$
precisely captures these signature jumps, this gives another explanation of why a contribution of K should not be expected in our formula.
Notice, furthermore, that Theorem 4.19 takes a particularly simple form for connected sums. Indeed, in this case, we have
![]() $w=1$
(so
$w=1$
(so
![]() $h=1$
) as well as
$h=1$
) as well as
![]() $\eta =\mu _P$
so that we obtain the following corollary.
$\eta =\mu _P$
so that we obtain the following corollary.
Corollary 4.21. Let
![]() $K, P$
be two knots. If
$K, P$
be two knots. If
![]() $\chi \colon H_1(\Sigma _n(K \# P);\mathbb {Z}) \to \mathbb {Z}_{m}$
is a character of prime power order, then
$\chi \colon H_1(\Sigma _n(K \# P);\mathbb {Z}) \to \mathbb {Z}_{m}$
is a character of prime power order, then
![]() $\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(K \# P)$
is Witt equivalent to
$\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(K \# P)$
is Witt equivalent to
![]() $\operatorname {\mathrm {Bl}}_{\alpha (n,\chi _P)}(P) \oplus \operatorname {\mathrm {Bl}}_{\alpha (n,\chi _K)}(K)$
.
$\operatorname {\mathrm {Bl}}_{\alpha (n,\chi _P)}(P) \oplus \operatorname {\mathrm {Bl}}_{\alpha (n,\chi _K)}(K)$
.
The remainder of this subsection is devoted to the proof of Theorem 4.19. We start by proving the
![]() $\eta $
-regularity of
$\eta $
-regularity of
![]() $\alpha (n,\chi )$
.
$\alpha (n,\chi )$
.
Lemma 4.22. Let
![]() $K,P$
be knots and let
$K,P$
be knots and let
![]() $\eta \subset S^3 \setminus P \subset M_P$
be a simple closed curve. Choose a character
$\eta \subset S^3 \setminus P \subset M_P$
be a simple closed curve. Choose a character
![]() $\chi \colon H_1(\Sigma _n(P(K,\eta ));\mathbb {Z}) \to \mathbb {Z}_{m} $
of finite order and let
$\chi \colon H_1(\Sigma _n(P(K,\eta ));\mathbb {Z}) \to \mathbb {Z}_{m} $
of finite order and let
![]() $w = \operatorname {\mathrm {lk}}(\eta ,P)$
.
$w = \operatorname {\mathrm {lk}}(\eta ,P)$
.
-
(1) If
 $w \neq 0$
, then
$w \neq 0$
, then
 $\alpha (n,\chi )$
is
$\alpha (n,\chi )$
is
 $\eta $
-regular.
$\eta $
-regular. -
(2) For
 $w=0$
,
$w=0$
,
 $\alpha (n,\chi )$
is
$\alpha (n,\chi )$
is
 $\eta $
-regular if and only if
$\eta $
-regular if and only if
 $\chi _i(q_Q(\mu _K^{-w}\eta )) \neq 0$
for each
$\chi _i(q_Q(\mu _K^{-w}\eta )) \neq 0$
for each
 $i=1,\ldots ,n$
.
$i=1,\ldots ,n$
.
Proof. Notice that in
![]() $M_{P(K,\eta )}$
, the meridian
$M_{P(K,\eta )}$
, the meridian
![]() $\mu _{\eta }$
of
$\mu _{\eta }$
of
![]() $\eta $
is identified with the zero-framed longitude of K. In particular, since the longitude of K is contained in
$\eta $
is identified with the zero-framed longitude of K. In particular, since the longitude of K is contained in
![]() $\pi _{1}(S^{3} \setminus \mathcal {N}(K))^{(2)}$
, it follows that
$\pi _{1}(S^{3} \setminus \mathcal {N}(K))^{(2)}$
, it follows that
![]() $\mu _{\eta } \in \pi _{1}(M_{P(K,\eta )})^{(2)}$
. Therefore, since the representation
$\mu _{\eta } \in \pi _{1}(M_{P(K,\eta )})^{(2)}$
. Therefore, since the representation
![]() $\alpha (n,\chi )$
is metabelian, we deduce that
$\alpha (n,\chi )$
is metabelian, we deduce that
![]() $\alpha (n,\chi )(\mu _{\eta }) =~1$
.
$\alpha (n,\chi )(\mu _{\eta }) =~1$
.
It remains to show that
![]() $\det \left (\alpha (n,\chi )(\eta ) - \operatorname {id}\right ) \neq 0$
. For
$\det \left (\alpha (n,\chi )(\eta ) - \operatorname {id}\right ) \neq 0$
. For
![]() $a_{1},\ldots ,a_{n}$
in
$a_{1},\ldots ,a_{n}$
in
![]() ${\mathbb {C}}[t^{\pm 1}]$
, define
${\mathbb {C}}[t^{\pm 1}]$
, define
![]() $\operatorname {diag}(a_{1},\ldots ,a_{n})$
to be the diagonal matrix with the
$\operatorname {diag}(a_{1},\ldots ,a_{n})$
to be the diagonal matrix with the
![]() $a_i$
on its main diagonal. The second assertion will quickly follow from the following observation:
$a_i$
on its main diagonal. The second assertion will quickly follow from the following observation:
Claim. Set
![]() $D = \operatorname {diag}(a_{1},a_{2},\ldots ,a_{n})$
and
$D = \operatorname {diag}(a_{1},a_{2},\ldots ,a_{n})$
and
 $A_n(t)= \left (\begin {smallmatrix} 0& 1 & \cdots &0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \\ t & 0 & \cdots & 0 \end {smallmatrix}\right )$
. For
$A_n(t)= \left (\begin {smallmatrix} 0& 1 & \cdots &0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \\ t & 0 & \cdots & 0 \end {smallmatrix}\right )$
. For
![]() $k\in \mathbb {Z}$
and
$k\in \mathbb {Z}$
and
![]() $h = \gcd (n,k)$
, the following equality holds:
$h = \gcd (n,k)$
, the following equality holds:
 $$\begin{align*}\det \left(A_{n}(t)^{k} D-\operatorname{id}\right) = \begin{cases} (a_1-1)\cdots(a_n-1) \quad &\text{if } k = 0, \\ \pm \prod_{i=1}^{h}(1-t^{k/h} a_{i} a_{i+h} \cdots a_{i+k-h}) \quad &\text{if } k \neq 0. \end{cases} \end{align*}$$
$$\begin{align*}\det \left(A_{n}(t)^{k} D-\operatorname{id}\right) = \begin{cases} (a_1-1)\cdots(a_n-1) \quad &\text{if } k = 0, \\ \pm \prod_{i=1}^{h}(1-t^{k/h} a_{i} a_{i+h} \cdots a_{i+k-h}) \quad &\text{if } k \neq 0. \end{cases} \end{align*}$$
Proof. If
![]() $k = 0$
, then the claim is clear. We therefore assume that
$k = 0$
, then the claim is clear. We therefore assume that
![]() $k \neq 0$
. If
$k \neq 0$
. If
![]() $h\neq 1$
, then a computation using the definition of
$h\neq 1$
, then a computation using the definition of
![]() $A_n(t)$
implies that there is a permutation matrix
$A_n(t)$
implies that there is a permutation matrix
![]() $B_{n,k}$
such that
$B_{n,k}$
such that
 $$\begin{align*}B_{n,k} \left(A_{n}(t)^{k} D-\operatorname{id}\right) B_{n,k}^{-1} = \bigoplus_{i=1}^{h} \left(A_{n/h}(t)^{k/h} \operatorname{diag}(a_{i},a_{i+h},\ldots)-\operatorname{id}\right).\end{align*}$$
$$\begin{align*}B_{n,k} \left(A_{n}(t)^{k} D-\operatorname{id}\right) B_{n,k}^{-1} = \bigoplus_{i=1}^{h} \left(A_{n/h}(t)^{k/h} \operatorname{diag}(a_{i},a_{i+h},\ldots)-\operatorname{id}\right).\end{align*}$$
We can therefore restrict our attention to the case
![]() $h=1$
. In this case, elementary row operations can be used to kill the entries below the diagonal. Eventually, we end up with a matrix with zeros below the main diagonal and the following entries on the main diagonal:
$h=1$
. In this case, elementary row operations can be used to kill the entries below the diagonal. Eventually, we end up with a matrix with zeros below the main diagonal and the following entries on the main diagonal:
 $$\begin{align*}\underbrace{-1,-1,\ldots,-1}_{n-1}, -1 + a_{1} a_{2} \cdots a_{n} t^{k}.\end{align*}$$
$$\begin{align*}\underbrace{-1,-1,\ldots,-1}_{n-1}, -1 + a_{1} a_{2} \cdots a_{n} t^{k}.\end{align*}$$
Thus, the determinant is equal to
![]() $(-1)^{n-1}(a_{1} a_{2} \cdots a_{n}t^{k}-1)$
, concluding the proof of the claim.
$(-1)^{n-1}(a_{1} a_{2} \cdots a_{n}t^{k}-1)$
, concluding the proof of the claim.
Use
![]() $\phi \colon \pi _1(M_{P(K,\eta )}) \to \mathbb {Z}$
to denote the abelianization map. We will apply the claim to
$\phi \colon \pi _1(M_{P(K,\eta )}) \to \mathbb {Z}$
to denote the abelianization map. We will apply the claim to
![]() $k=\phi (\eta )=w$
and
$k=\phi (\eta )=w$
and
![]() $a_i=\chi _i(q_Q(\mu _Q^{-w}\eta ))$
. If
$a_i=\chi _i(q_Q(\mu _Q^{-w}\eta ))$
. If
![]() $w \neq 0$
, then the claim implies that
$w \neq 0$
, then the claim implies that
![]() $\det \left (\alpha (n,\chi )(\eta ) - \operatorname {id}\right ) \neq 0$
, proving the first assertion. If
$\det \left (\alpha (n,\chi )(\eta ) - \operatorname {id}\right ) \neq 0$
, proving the first assertion. If
![]() $w=0$
, then the claim implies that
$w=0$
, then the claim implies that
![]() $\det \left (\alpha (n,\chi )(\eta ) - \operatorname {id}\right ) \neq 0$
if and only if none of the
$\det \left (\alpha (n,\chi )(\eta ) - \operatorname {id}\right ) \neq 0$
if and only if none of the
![]() $a_i$
is equal to
$a_i$
is equal to
![]() $1$
. This concludes the proof of the second assertion and therefore the proof of the lemma.
$1$
. This concludes the proof of the second assertion and therefore the proof of the lemma.
We now suppose that
![]() $\alpha (n,\chi )$
is
$\alpha (n,\chi )$
is
![]() $\eta $
-regular (this is automatic for
$\eta $
-regular (this is automatic for
![]() $w \neq 0$
). Thus,
$w \neq 0$
). Thus,
![]() $\alpha (n,\chi )$
restricts to representations
$\alpha (n,\chi )$
restricts to representations
![]() $\alpha (n,\chi )_K$
and
$\alpha (n,\chi )_K$
and
![]() $\alpha (n,\chi )_P=\alpha (n,\chi _P)$
on the fundamental groups of
$\alpha (n,\chi )_P=\alpha (n,\chi _P)$
on the fundamental groups of
![]() $M_P$
and
$M_P$
and
![]() $M_K$
. Before applying Theorem 3.11 to obtain a decomposition of
$M_K$
. Before applying Theorem 3.11 to obtain a decomposition of
![]() $\operatorname {Bl}_{\alpha (n,\chi )}(M_{P(K,\eta )})$
, we start by studying
$\operatorname {Bl}_{\alpha (n,\chi )}(M_{P(K,\eta )})$
, we start by studying
![]() $\alpha (n,\chi )_K$
. The next remark leads to the main idea in this process.
$\alpha (n,\chi )_K$
. The next remark leads to the main idea in this process.
Remark 4.23. Set
![]() $G:=\mathbb {Z} \ltimes H_1(\Sigma _n(P(K,\eta ));\mathbb {Z})$
. Recall from Subsection 4.1 that the metabelian representation
$G:=\mathbb {Z} \ltimes H_1(\Sigma _n(P(K,\eta ));\mathbb {Z})$
. Recall from Subsection 4.1 that the metabelian representation
![]() $\alpha (n,\chi ) \colon \pi _1(M_{P(K,\eta )}) \to GL_n({\mathbb {C}}[t^{\pm 1}])$
is defined as the composition of the map
$\alpha (n,\chi ) \colon \pi _1(M_{P(K,\eta )}) \to GL_n({\mathbb {C}}[t^{\pm 1}])$
is defined as the composition of the map
![]() $\widetilde {\rho }_{Q} \colon \pi _1(M_{P(K,\eta )}) \to ~G$
of (4.2) with the representation
$\widetilde {\rho }_{Q} \colon \pi _1(M_{P(K,\eta )}) \to ~G$
of (4.2) with the representation
![]() $\gamma _Q(n,\chi ) \colon G \to GL_n({\mathbb {C}}[t^{\pm 1}])$
described in (4.1). Recalling the definition of
$\gamma _Q(n,\chi ) \colon G \to GL_n({\mathbb {C}}[t^{\pm 1}])$
described in (4.1). Recalling the definition of
![]() $\iota _*$
from (4.17) as well as the definition of
$\iota _*$
from (4.17) as well as the definition of
![]() $\iota _n$
from (4.18), the inclusion map
$\iota _n$
from (4.18), the inclusion map
![]() $ S^3 \setminus \mathcal {N}(K) \to ~M_{P(K,\eta )}$
gives rise to the following commutative diagram:
$ S^3 \setminus \mathcal {N}(K) \to ~M_{P(K,\eta )}$
gives rise to the following commutative diagram:

where
![]() $\operatorname {proj}_{0}(t_{Q}^{\ell }, (x_{1}, t_{Q}x_{2},\ldots ,t_{Q}^{h-1}x_{h})) = (t_{Q}^{\ell },x_{1})$
and
$\operatorname {proj}_{0}(t_{Q}^{\ell }, (x_{1}, t_{Q}x_{2},\ldots ,t_{Q}^{h-1}x_{h})) = (t_{Q}^{\ell },x_{1})$
and
![]() $ \operatorname {incl}_{0}(t_{Q}^{\ell }, x) = (t_{Q}^{\ell }, (x, 0, \ldots , 0)).$
Since
$ \operatorname {incl}_{0}(t_{Q}^{\ell }, x) = (t_{Q}^{\ell }, (x, 0, \ldots , 0)).$
Since
we must study the restriction of
![]() $\gamma _Q(n,\chi )$
to
$\gamma _Q(n,\chi )$
to
![]() $H_1:=\operatorname {im}(\iota _n)$
. We shall denote this restriction by
$H_1:=\operatorname {im}(\iota _n)$
. We shall denote this restriction by
![]() $\operatorname {\mathrm {res}}^{G}_{H_1} \gamma _Q(n,\chi )$
. Next, set
$\operatorname {\mathrm {res}}^{G}_{H_1} \gamma _Q(n,\chi )$
. Next, set
![]() $H_2:=n\mathbb {Z} \times H_1(\Sigma _n(Q);\mathbb {Z})$
and recall from Remark 4.5 that
$H_2:=n\mathbb {Z} \times H_1(\Sigma _n(Q);\mathbb {Z})$
and recall from Remark 4.5 that
![]() $\gamma _Q(n,\chi )$
is isomorphic to the induced representation
$\gamma _Q(n,\chi )$
is isomorphic to the induced representation
![]() $\operatorname {\mathrm {ind}}^{G}_{H} \rho _Q(n,\chi ).$
Thus, in order to understand
$\operatorname {\mathrm {ind}}^{G}_{H} \rho _Q(n,\chi ).$
Thus, in order to understand
![]() $\alpha (n,\chi )_K$
, we must study
$\alpha (n,\chi )_K$
, we must study
Remark 4.23 calls for an application of Mackey’s induction formula. In order to recall this result, we start with a group G and two subgroups
![]() $H_{1},H_{2} \subset G$
. For any
$H_{1},H_{2} \subset G$
. For any
![]() $a \in G$
, there is a double
$a \in G$
, there is a double
![]() $(H_{1},H_{2})$
-coset
$(H_{1},H_{2})$
-coset
![]() $H_{1} a H_{2} := \{h_{1} a h_{2} \mid h_{1} \in H_{1}, h_{2} \in H_{2}\} \subset G$
. It is easy to see that
$H_{1} a H_{2} := \{h_{1} a h_{2} \mid h_{1} \in H_{1}, h_{2} \in H_{2}\} \subset G$
. It is easy to see that
![]() $H_{1} a H_{2} = H_{1} b H_{2}$
if and only if there are
$H_{1} a H_{2} = H_{1} b H_{2}$
if and only if there are
![]() $h_{1} \in H_{1}$
and
$h_{1} \in H_{1}$
and
![]() $h_{2} \in H_{2}$
such that
$h_{2} \in H_{2}$
such that
![]() $a = h_{1} b h_{2}$
. Denote the set of double
$a = h_{1} b h_{2}$
. Denote the set of double
![]() $(H_{1},H_{2})$
-cosets by
$(H_{1},H_{2})$
-cosets by
![]() $H_{1} \backslash G / H_{2}$
. If
$H_{1} \backslash G / H_{2}$
. If
![]() $a \in G$
and
$a \in G$
and
![]() $\rho $
is a representation of
$\rho $
is a representation of
![]() $H_{2}$
, then we will denote by
$H_{2}$
, then we will denote by
![]() ${}^{a}\rho $
the representation of
${}^{a}\rho $
the representation of
![]() $aH_{2}a^{-1}$
given by the formula
$aH_{2}a^{-1}$
given by the formula
![]() ${}^{a}\rho (x)= \rho (a^{-1}xa).$
${}^{a}\rho (x)= \rho (a^{-1}xa).$
With these notations, Mackey’s formula reads as follows; see [Reference Curtis and Reiner16, Theorem 10.13].
Theorem 4.24. Let G be a group and let
![]() $H_{1},H_{2} \subset G$
be finite index subgroups. If
$H_{1},H_{2} \subset G$
be finite index subgroups. If
![]() $\rho $
is a representation of
$\rho $
is a representation of
![]() $H_{2}$
, then we have
$H_{2}$
, then we have
 $$\begin{align*}\operatorname{\mathrm{res}}^{G}_{H_{1}} \operatorname{\mathrm{ind}}^{G}_{H_{2}}(\rho) = \bigoplus_{H_{1} a H_{2}} \operatorname{\mathrm{ind}}^{H_{1}}_{aH_{2}a^{-1} \cap H_{1}} \operatorname{\mathrm{res}}^{aH_{2}a^{-1}}_{aH_{2}a^{-1} \cap H_{1}} ({}^{a} \rho),\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{res}}^{G}_{H_{1}} \operatorname{\mathrm{ind}}^{G}_{H_{2}}(\rho) = \bigoplus_{H_{1} a H_{2}} \operatorname{\mathrm{ind}}^{H_{1}}_{aH_{2}a^{-1} \cap H_{1}} \operatorname{\mathrm{res}}^{aH_{2}a^{-1}}_{aH_{2}a^{-1} \cap H_{1}} ({}^{a} \rho),\end{align*}$$
where the sum is taken over all
![]() $H_{1} a H_{2} \in H_{1} \backslash G / H_{2}$
.
$H_{1} a H_{2} \in H_{1} \backslash G / H_{2}$
.
We will now apply Mackey’s formula to the group
![]() $G = \mathbb {Z} \ltimes H_{1}(\Sigma _{n}(P(K,\eta ));\mathbb {Z})$
and to the subgroups
$G = \mathbb {Z} \ltimes H_{1}(\Sigma _{n}(P(K,\eta ));\mathbb {Z})$
and to the subgroups
![]() $H_2 = n\mathbb {Z} \times H_{1}(\Sigma _{n}(P(K,\eta ));\mathbb {Z})$
and
$H_2 = n\mathbb {Z} \times H_{1}(\Sigma _{n}(P(K,\eta ));\mathbb {Z})$
and
![]() $H_1 = \operatorname {Im}(\iota _{n}).$
In order to carry this out, we need slight generalizations of our metabelian representations. Let J be an arbitrary knot. Given a complex number
$H_1 = \operatorname {Im}(\iota _{n}).$
In order to carry this out, we need slight generalizations of our metabelian representations. Let J be an arbitrary knot. Given a complex number
![]() $\theta \in S^{1}$
and an integer
$\theta \in S^{1}$
and an integer
![]() $\ell ~\in ~\mathbb {Z}$
, we consider the representation
$\ell ~\in ~\mathbb {Z}$
, we consider the representation
 $$ \begin{align} \gamma_J(n,\chi,\theta,\ell) \colon &\mathbb{Z} \ltimes H_{1}(\Sigma_{n}(K);\mathbb{Z}) \to GL_n({\mathbb{C}}[t^{\pm 1}]) \nonumber \\ &(t_Q^{a},x) \mapsto \begin{pmatrix} 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & & \vdots \\ 0 & 0 & 0 & \cdots & 1 \\ \theta t^{\ell} & 0 & 0 & \cdots & 0 \end{pmatrix}^{a} \begin{pmatrix} \xi_{m}^{\chi(x)} & 0 & 0 & \cdots & 0 \\ 0 & \xi_{m}^{\chi(t_J \cdot x)} & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & & \vdots \\ 0 & 0 & 0 & 0 & \xi_{m}^{\chi(t_J^{n-1}\cdot x)} \end{pmatrix}. \end{align} $$
$$ \begin{align} \gamma_J(n,\chi,\theta,\ell) \colon &\mathbb{Z} \ltimes H_{1}(\Sigma_{n}(K);\mathbb{Z}) \to GL_n({\mathbb{C}}[t^{\pm 1}]) \nonumber \\ &(t_Q^{a},x) \mapsto \begin{pmatrix} 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & & \vdots \\ 0 & 0 & 0 & \cdots & 1 \\ \theta t^{\ell} & 0 & 0 & \cdots & 0 \end{pmatrix}^{a} \begin{pmatrix} \xi_{m}^{\chi(x)} & 0 & 0 & \cdots & 0 \\ 0 & \xi_{m}^{\chi(t_J \cdot x)} & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & & \vdots \\ 0 & 0 & 0 & 0 & \xi_{m}^{\chi(t_J^{n-1}\cdot x)} \end{pmatrix}. \end{align} $$
By definition of this representation, we have the equality
![]() $\gamma _J(n,\chi ,1,1) = \gamma _J(n,\chi )$
. Next, we generalize the representation
$\gamma _J(n,\chi ,1,1) = \gamma _J(n,\chi )$
. Next, we generalize the representation
![]() $\rho _J(n,\chi )$
by considering the representation
$\rho _J(n,\chi )$
by considering the representation
 $$ \begin{align} \rho_J(n,\chi,\theta,\ell) \colon n\mathbb{Z} \times H_1(\Sigma_n(J);\mathbb{Z}) &\to {\mathbb{C}}[t^{\pm 1}] \\ (t_J^{nk},x) &\mapsto (\theta t^{\ell})^{k} \cdot \xi_{m}^{\chi(x)}. \nonumber \end{align} $$
$$ \begin{align} \rho_J(n,\chi,\theta,\ell) \colon n\mathbb{Z} \times H_1(\Sigma_n(J);\mathbb{Z}) &\to {\mathbb{C}}[t^{\pm 1}] \\ (t_J^{nk},x) &\mapsto (\theta t^{\ell})^{k} \cdot \xi_{m}^{\chi(x)}. \nonumber \end{align} $$
Just as for the representation
![]() $\gamma _J(n,\chi ,\theta ,\ell )$
, we observe that
$\gamma _J(n,\chi ,\theta ,\ell )$
, we observe that
![]() $\rho _J(n,\chi ,1,1)=\rho _J(n,\chi )$
. Furthermore, generalizing Remark 4.5, we also have the induction formula
$\rho _J(n,\chi ,1,1)=\rho _J(n,\chi )$
. Furthermore, generalizing Remark 4.5, we also have the induction formula
The following lemma gathers some results for our application of Mackey’s formula.
Lemma 4.25. The following assertions hold:
-
(1) Every double
 $(H_1,H_2)$
-coset is equal to
$(H_1,H_2)$
-coset is equal to
 $H_1(t_{Q}^{i},0)H_2$
, for some
$H_1(t_{Q}^{i},0)H_2$
, for some
 $1 \leq i \leq h$
.
$1 \leq i \leq h$
. -
(2)
 $H_2$
is a normal subgroup of G.
$H_2$
is a normal subgroup of G. -
(3) For any
 $(t_Q^k,x) \in G$
and any
$(t_Q^k,x) \in G$
and any
 $1 \leq i \leq h$
, we have
$1 \leq i \leq h$
, we have  $$ \begin{align*}{}^{t_{Q}^{i}} \rho_{Q}(n,\chi,\theta,\ell)(t_Q^k,x) = \rho_{Q}(n,\chi_{i},\theta,\ell)(t_Q^k,x).\end{align*} $$
$$ \begin{align*}{}^{t_{Q}^{i}} \rho_{Q}(n,\chi,\theta,\ell)(t_Q^k,x) = \rho_{Q}(n,\chi_{i},\theta,\ell)(t_Q^k,x).\end{align*} $$
-
(4) For any
 $(t_K^{n/h},x) \in H_1 \cap H_2$
, we have
$(t_K^{n/h},x) \in H_1 \cap H_2$
, we have  $$ \begin{align*}\operatorname{\mathrm{res}}_{H_2 \cap H_1}^{H_2} \rho_{Q}(n,\chi,\theta,\ell)(t_K^{n/h},x) = \rho_{K}(n/h,\chi,\theta^{w/h} \xi_{m}^{\chi(q_Q(\mu_K^{-w}\eta))},\ell w/h)(t_K^{n/h},x).\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{res}}_{H_2 \cap H_1}^{H_2} \rho_{Q}(n,\chi,\theta,\ell)(t_K^{n/h},x) = \rho_{K}(n/h,\chi,\theta^{w/h} \xi_{m}^{\chi(q_Q(\mu_K^{-w}\eta))},\ell w/h)(t_K^{n/h},x).\end{align*} $$
Proof. Given
![]() $g = (t_{Q}^d,x) $
in G, we study the
$g = (t_{Q}^d,x) $
in G, we study the
![]() $(H_1,H_2)$
-coset
$(H_1,H_2)$
-coset
![]() $H_1gH_2$
. We write
$H_1gH_2$
. We write
![]() $h=\operatorname {gcd}(n,w)$
as
$h=\operatorname {gcd}(n,w)$
as
![]() $h=an + bw $
as well as
$h=an + bw $
as well as
![]() $d = hs + r$
, for some
$d = hs + r$
, for some
![]() $0 \leq r \leq h-1$
. Furthermore, for
$0 \leq r \leq h-1$
. Furthermore, for
![]() $x \in H_{1}(\Sigma _{n}(P(K,\eta ));\mathbb {Z})$
, we set
$x \in H_{1}(\Sigma _{n}(P(K,\eta ));\mathbb {Z})$
, we set
![]() $\nu _{p}(t_Q) = t_{Q}^{-p+1}+t_{Q}^{-p+2}+\cdots +t_{Q}^{-1}+1$
. A computation now shows that
$\nu _{p}(t_Q) = t_{Q}^{-p+1}+t_{Q}^{-p+2}+\cdots +t_{Q}^{-1}+1$
. A computation now shows that
To show that the right-hand side belongs to
![]() $H_1(t_{Q}^r,0)H_2$
, we only need to prove that
$H_1(t_{Q}^r,0)H_2$
, we only need to prove that
![]() $(t_{Q}^{w},q_Q(\mu _K^{-w}\eta ))$
belongs to
$(t_{Q}^{w},q_Q(\mu _K^{-w}\eta ))$
belongs to
![]() $H_1=\operatorname {im}(i_n)$
. This follows from the diagram in (4.19) which implies that
$H_1=\operatorname {im}(i_n)$
. This follows from the diagram in (4.19) which implies that
The second assertion is a consequence of the definition of the group law on G. We now prove the third assertion. Given
![]() $(t_Q^k,x) \in G$
and
$(t_Q^k,x) \in G$
and
![]() $0 \leq i \leq h-1$
, we apply successively the definition of
$0 \leq i \leq h-1$
, we apply successively the definition of
![]() $ {}^{a} \rho $
, the group law in G and the definition of
$ {}^{a} \rho $
, the group law in G and the definition of
![]() $\chi _i$
to obtain the desired equality:
$\chi _i$
to obtain the desired equality:
 $$ \begin{align*} {}^{t_{Q}^{i}} \rho_{Q}(n,\chi,\theta,\ell)(t_{Q}^{k},x) &= \rho_{Q}(n,\chi,\theta,\ell)((t_{Q}^{-i},0) (t_{Q}^{k},x)(t_{Q}^{i},0)) \\ &= \rho_{Q}(n,\chi,\theta,\ell)(t_{Q}^{k},t_{Q}^{-i}\cdot x) \\ &=\rho_{Q}(n,\chi_{i},\theta,\ell)(t_{Q}^{k},x). \end{align*} $$
$$ \begin{align*} {}^{t_{Q}^{i}} \rho_{Q}(n,\chi,\theta,\ell)(t_{Q}^{k},x) &= \rho_{Q}(n,\chi,\theta,\ell)((t_{Q}^{-i},0) (t_{Q}^{k},x)(t_{Q}^{i},0)) \\ &= \rho_{Q}(n,\chi,\theta,\ell)(t_{Q}^{k},t_{Q}^{-i}\cdot x) \\ &=\rho_{Q}(n,\chi_{i},\theta,\ell)(t_{Q}^{k},x). \end{align*} $$
To prove the fourth assertion, we first note that
![]() $H_2 \cap H_1=\operatorname {im} \left (\iota _{n}|_{(n/h)\mathbb {Z} \times H_{1}(\Sigma _{n/h}(K);\mathbb {Z})}\right )$
. Next, using the relation
$H_2 \cap H_1=\operatorname {im} \left (\iota _{n}|_{(n/h)\mathbb {Z} \times H_{1}(\Sigma _{n/h}(K);\mathbb {Z})}\right )$
. Next, using the relation
![]() $\iota _{n}(t_{K},0) = (t_{Q}^{w},q_Q(\mu _K^{-w}\eta ))$
and the definition of
$\iota _{n}(t_{K},0) = (t_{Q}^{w},q_Q(\mu _K^{-w}\eta ))$
and the definition of
![]() $\rho (n,\chi ,\theta ,\ell )$
, we obtain
$\rho (n,\chi ,\theta ,\ell )$
, we obtain
 $$ \begin{align*} \left(\operatorname{\mathrm{res}}_{H_2 \cap H_1}^{H_2} \rho_{Q}(n,\chi,\theta,w)\right)(t_{K}^{n/h},0) &= \rho_{Q}(n,\chi,\theta,\ell)(t_{Q}^{wn/h},q_Q(\mu_K^{-w}\eta)) \\ &= (\theta t^{\ell})^{w/h} \xi_{m}^{\chi(q_Q(\mu_K^{-w}\eta))} \\ &=\rho_{K}(n/h,\chi,\theta^{w/h} \xi_{m}^{\chi(q_Q(\mu_K^{-w}\eta))},\ell w/h))(t_{K}^{n/h},0). \end{align*} $$
$$ \begin{align*} \left(\operatorname{\mathrm{res}}_{H_2 \cap H_1}^{H_2} \rho_{Q}(n,\chi,\theta,w)\right)(t_{K}^{n/h},0) &= \rho_{Q}(n,\chi,\theta,\ell)(t_{Q}^{wn/h},q_Q(\mu_K^{-w}\eta)) \\ &= (\theta t^{\ell})^{w/h} \xi_{m}^{\chi(q_Q(\mu_K^{-w}\eta))} \\ &=\rho_{K}(n/h,\chi,\theta^{w/h} \xi_{m}^{\chi(q_Q(\mu_K^{-w}\eta))},\ell w/h))(t_{K}^{n/h},0). \end{align*} $$
To get the equality for arbitrary elements
![]() $(t_{K}^{n/h},x) \in H_1 \cap H_2$
, note that the value of both homomorphisms on
$(t_{K}^{n/h},x) \in H_1 \cap H_2$
, note that the value of both homomorphisms on
![]() $(1,x)$
is
$(1,x)$
is
![]() $\xi _m^{\chi (\iota _n(x))}.$
This concludes the proof of the lemma.
$\xi _m^{\chi (\iota _n(x))}.$
This concludes the proof of the lemma.
Lemma 4.25 is now used to apply Mackey’s theorem to our setting.
Proposition 4.26. Use
![]() $\gamma _Q(n,\chi )_{K}$
to denote the restriction of
$\gamma _Q(n,\chi )_{K}$
to denote the restriction of
![]() $\gamma _Q(n,\chi )$
to
$\gamma _Q(n,\chi )$
to
![]() $\mathbb {Z} \ltimes H_1(\Sigma _{n/h}(K),\mathbb {Z})$
. There exists an isomorphism of representations
$\mathbb {Z} \ltimes H_1(\Sigma _{n/h}(K),\mathbb {Z})$
. There exists an isomorphism of representations
 $$\begin{align*}\gamma_{Q}(n,\chi)_{K} \cong \bigoplus_{i=1}^{h} \gamma_{K}(n/h,\chi_{i},\xi_{m}^{\chi_{i}(q_Q(\mu_K^{-w}\eta))},w/h).\end{align*}$$
$$\begin{align*}\gamma_{Q}(n,\chi)_{K} \cong \bigoplus_{i=1}^{h} \gamma_{K}(n/h,\chi_{i},\xi_{m}^{\chi_{i}(q_Q(\mu_K^{-w}\eta))},w/h).\end{align*}$$
Proof. Since we saw in Remark 4.23 that
![]() $\gamma (n,\chi )_{K} = \operatorname {\mathrm {res}}^{G}_{H_1} \operatorname {\mathrm {ind}}^{G}_{H_2} \rho _{Q}(n,\chi ),$
our goal is to apply Mackey’s formula to
$\gamma (n,\chi )_{K} = \operatorname {\mathrm {res}}^{G}_{H_1} \operatorname {\mathrm {ind}}^{G}_{H_2} \rho _{Q}(n,\chi ),$
our goal is to apply Mackey’s formula to
![]() $\rho _Q(n,\chi )=\rho _Q(n,\chi ,1,1)$
. For the remainder of the proof, we write
$\rho _Q(n,\chi )=\rho _Q(n,\chi ,1,1)$
. For the remainder of the proof, we write
![]() $\rho $
as a shorthand for
$\rho $
as a shorthand for
![]() $\rho _Q(n,\chi ,\theta ,\chi )$
. Using consecutively Theorem 4.24 (as well as the first item of Lemma 4.25), and then the second, third and fourth items of Lemma 4.25, we obtain
$\rho _Q(n,\chi ,\theta ,\chi )$
. Using consecutively Theorem 4.24 (as well as the first item of Lemma 4.25), and then the second, third and fourth items of Lemma 4.25, we obtain
 $$ \begin{align*} \operatorname{\mathrm{res}}^{G}_{H_{1}} \operatorname{\mathrm{ind}}^{G}_{H_{2}}(\rho) &= \bigoplus_{i=1}^{h} \operatorname{\mathrm{ind}}^{H_1}_{H_2 \cap H_1} \operatorname{\mathrm{res}}^{H_2}_{H_2 \cap H_{1}} ({}^{t_Q^i} \rho) \\ &= \bigoplus_{i=1}^{h} \operatorname{\mathrm{ind}}^{H_1}_{H_2 \cap H_1} \operatorname{\mathrm{res}}^{H_2}_{H_2 \cap H_{1}} (\rho_{Q}(n,\chi_{i},\theta,\ell)) \\ &= \bigoplus_{i=1}^{h} \operatorname{\mathrm{ind}}^{H_1}_{H_2 \cap H_1}\rho_{K}(n/h,\chi_i,\theta^{w/h} \xi_{m}^{\chi_i(q_Q(\mu_K^{-w}\eta))},\ell w/h)). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{res}}^{G}_{H_{1}} \operatorname{\mathrm{ind}}^{G}_{H_{2}}(\rho) &= \bigoplus_{i=1}^{h} \operatorname{\mathrm{ind}}^{H_1}_{H_2 \cap H_1} \operatorname{\mathrm{res}}^{H_2}_{H_2 \cap H_{1}} ({}^{t_Q^i} \rho) \\ &= \bigoplus_{i=1}^{h} \operatorname{\mathrm{ind}}^{H_1}_{H_2 \cap H_1} \operatorname{\mathrm{res}}^{H_2}_{H_2 \cap H_{1}} (\rho_{Q}(n,\chi_{i},\theta,\ell)) \\ &= \bigoplus_{i=1}^{h} \operatorname{\mathrm{ind}}^{H_1}_{H_2 \cap H_1}\rho_{K}(n/h,\chi_i,\theta^{w/h} \xi_{m}^{\chi_i(q_Q(\mu_K^{-w}\eta))},\ell w/h)). \end{align*} $$
Since
![]() $H_2 \cap H_1=\operatorname {im} \left (\iota _{n}|_{(n/h)\mathbb {Z} \times H_{1}(\Sigma _{n/h}(K);\mathbb {Z})}\right )$
, observe that
$H_2 \cap H_1=\operatorname {im} \left (\iota _{n}|_{(n/h)\mathbb {Z} \times H_{1}(\Sigma _{n/h}(K);\mathbb {Z})}\right )$
, observe that
![]() $\operatorname {\mathrm {ind}}_{H_1 \cap H_2}^G \rho _K(n,\chi ,\theta ,\ell )=\gamma _K(n,\chi ,\theta ,\ell )$
. Additionally, recall that
$\operatorname {\mathrm {ind}}_{H_1 \cap H_2}^G \rho _K(n,\chi ,\theta ,\ell )=\gamma _K(n,\chi ,\theta ,\ell )$
. Additionally, recall that
![]() $\gamma _Q(n,\chi )_{K} = \operatorname {\mathrm {res}}^{G}_{H_1} \operatorname {\mathrm {ind}}^{G}_{H_2} \rho _{Q}(n,\chi ,1,1)$
and
$\gamma _Q(n,\chi )_{K} = \operatorname {\mathrm {res}}^{G}_{H_1} \operatorname {\mathrm {ind}}^{G}_{H_2} \rho _{Q}(n,\chi ,1,1)$
and
![]() $\gamma _Q(n,\chi )=\gamma _Q(n,\chi ,1,1)$
. Therefore, taking
$\gamma _Q(n,\chi )=\gamma _Q(n,\chi ,1,1)$
. Therefore, taking
![]() $\theta =1$
and
$\theta =1$
and
![]() $\ell =1$
in the previous computation, we obtain
$\ell =1$
in the previous computation, we obtain
 $$ \begin{align*} \gamma_Q(n,\chi)_{K} =\operatorname{\mathrm{res}}^{G}_{H_{1}} \operatorname{\mathrm{ind}}^{G}_{H_{2}}(\rho_Q(n,\chi)) =\bigoplus_{i=1}^{h} \gamma_{K}(n/h,\chi_{i},\xi_{m}^{\chi_{i}(q_Q(\mu_K^{-w}\eta))},w/h). \end{align*} $$
$$ \begin{align*} \gamma_Q(n,\chi)_{K} =\operatorname{\mathrm{res}}^{G}_{H_{1}} \operatorname{\mathrm{ind}}^{G}_{H_{2}}(\rho_Q(n,\chi)) =\bigoplus_{i=1}^{h} \gamma_{K}(n/h,\chi_{i},\xi_{m}^{\chi_{i}(q_Q(\mu_K^{-w}\eta))},w/h). \end{align*} $$
This concludes the proof of the proposition.
Next, we return to Blanchfield pairings. Namely, we discuss the effect of the representation
![]() $\gamma _Q(n,\chi ,\theta ,\ell )$
on the variable t of the metabelian Blanchfield pairing.
$\gamma _Q(n,\chi ,\theta ,\ell )$
on the variable t of the metabelian Blanchfield pairing.
Remark 4.27. Recall from Subsection 4.1 that for any knot J, the representation
![]() $\alpha _J(n,\chi )$
is obtained by precomposing the representation
$\alpha _J(n,\chi )$
is obtained by precomposing the representation
![]() $\gamma _J(n,\chi ) \colon \mathbb {Z} \ltimes H_1(\Sigma _n(J);\mathbb {Z}) \to GL_n({\mathbb {C}}[t^{\pm 1}])$
with the map
$\gamma _J(n,\chi ) \colon \mathbb {Z} \ltimes H_1(\Sigma _n(J);\mathbb {Z}) \to GL_n({\mathbb {C}}[t^{\pm 1}])$
with the map
![]() $\widetilde {\rho }_J \colon \pi _1(M_J) \to \mathbb {Z} \ltimes H_1(\Sigma _n(J);\mathbb {Z})$
. We shall adopt the same convention for
$\widetilde {\rho }_J \colon \pi _1(M_J) \to \mathbb {Z} \ltimes H_1(\Sigma _n(J);\mathbb {Z})$
. We shall adopt the same convention for
![]() $\gamma _J(n,\chi ,\theta ,\ell )$
, thus obtaining a representation
$\gamma _J(n,\chi ,\theta ,\ell )$
, thus obtaining a representation
![]() $\alpha _J(n,\chi ,\theta ,\ell )$
of
$\alpha _J(n,\chi ,\theta ,\ell )$
of
![]() $\pi _1(M_J)$
. Since
$\pi _1(M_J)$
. Since
![]() $\gamma _J(n,\chi ,\theta ,\ell )$
can be obtained from
$\gamma _J(n,\chi ,\theta ,\ell )$
can be obtained from
![]() $\gamma _J(n,\chi )$
via the substitution
$\gamma _J(n,\chi )$
via the substitution
![]() $t \mapsto \theta t^{\ell }$
, it follows that
$t \mapsto \theta t^{\ell }$
, it follows that
![]() $\operatorname {\mathrm {Bl}}_{\alpha (n,\chi ,\theta ,\ell )}(J)(t)=\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(J)(\theta t^\ell )$
.
$\operatorname {\mathrm {Bl}}_{\alpha (n,\chi ,\theta ,\ell )}(J)(t)=\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(J)(\theta t^\ell )$
.
Returning to satellite knots, recall from Remark 4.23 that the Blanchfield pairing
![]() $\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )_K}(K)$
is obtained by precomposing the representation
$\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )_K}(K)$
is obtained by precomposing the representation
![]() $\gamma _Q(n,\chi )_K \colon \mathbb {Z} \ltimes H_1(\Sigma _{n/h}(K);\mathbb {Z}) \to GL_n({\mathbb {C}}[t^{\pm 1}])$
with the map
$\gamma _Q(n,\chi )_K \colon \mathbb {Z} \ltimes H_1(\Sigma _{n/h}(K);\mathbb {Z}) \to GL_n({\mathbb {C}}[t^{\pm 1}])$
with the map
![]() $\widetilde {\rho }_{K,Q} \colon \pi _1(M_K) \to \mathbb {Z} \ltimes H_1(\Sigma _{n/h}(K);\mathbb {Z})$
. Thus, applying Proposition 4.26 and Remark 4.27, we obtain the following isometry of linking forms:
$\widetilde {\rho }_{K,Q} \colon \pi _1(M_K) \to \mathbb {Z} \ltimes H_1(\Sigma _{n/h}(K);\mathbb {Z})$
. Thus, applying Proposition 4.26 and Remark 4.27, we obtain the following isometry of linking forms:
 $$ \begin{align} \operatorname{\mathrm{Bl}}_{\alpha(n,\chi)_K}(K)(t) \cong \bigoplus_{i=1}^{h} \operatorname{\mathrm{Bl}}_{\alpha_K(n/h,\chi)}(K)(\chi_{i}(q_Q(\mu_K^{-w}\eta))t^{w/h}). \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Bl}}_{\alpha(n,\chi)_K}(K)(t) \cong \bigoplus_{i=1}^{h} \operatorname{\mathrm{Bl}}_{\alpha_K(n/h,\chi)}(K)(\chi_{i}(q_Q(\mu_K^{-w}\eta))t^{w/h}). \end{align} $$
Using this isometry, we can now prove Theorem 4.19.
Proof of Theorem 4.19
First of all, note that Lemma 4.22 ensures that
![]() $\alpha (n,\chi )$
is
$\alpha (n,\chi )$
is
![]() $\eta $
-regular. We can therefore apply the satellite formula of Theorem 3.11 to each of the cases which we shall now distinguish.
$\eta $
-regular. We can therefore apply the satellite formula of Theorem 3.11 to each of the cases which we shall now distinguish.
We first assume that
![]() $w \neq ~0$
. As
$w \neq ~0$
. As
![]() $\alpha (n,\chi )$
is
$\alpha (n,\chi )$
is
![]() $\eta $
-regular, it restricts to representations
$\eta $
-regular, it restricts to representations
![]() $\alpha (n,\chi )_K$
and
$\alpha (n,\chi )_K$
and
![]() $\alpha (n,\chi )_P$
on
$\alpha (n,\chi )_P$
on
![]() $\pi _1(M_K)$
and
$\pi _1(M_K)$
and
![]() $\pi _1(M_P)$
. We consider two cases.
$\pi _1(M_P)$
. We consider two cases.
Case 1. If w is divisible by n, then
![]() $\alpha (n,\chi )_K$
is abelian and is isomorphic to
$\alpha (n,\chi )_K$
is abelian and is isomorphic to
![]() $\bigoplus _{i=1}^n \xi _m^{\chi _i} \otimes ~\phi _K^{w/n}$
, where
$\bigoplus _{i=1}^n \xi _m^{\chi _i} \otimes ~\phi _K^{w/n}$
, where
![]() $\xi _m^{\chi _i}$
is understood as the character mapping the meridian
$\xi _m^{\chi _i}$
is understood as the character mapping the meridian
![]() $\mu _K$
to
$\mu _K$
to
![]() $\xi _m^{\chi _i(q_Q(\mu _Q^{-w}\eta ))}$
. As a consequence, (4.22) and Corollary 3.15 provide the desired isometry of linking forms:
$\xi _m^{\chi _i(q_Q(\mu _Q^{-w}\eta ))}$
. As a consequence, (4.22) and Corollary 3.15 provide the desired isometry of linking forms:
 $$\begin{align*}\operatorname{\mathrm{Bl}}_{\alpha(n,\chi)}(P(K,\eta)) \cong \operatorname{\mathrm{Bl}}_{\alpha(n,\chi_P)}(P) \oplus \bigoplus_{i=1}^{n} \operatorname{\mathrm{Bl}}(K)(\xi_m^{\chi_{i}(q_Q(\mu_K^{-w}\eta))}t^{w/n}).\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Bl}}_{\alpha(n,\chi)}(P(K,\eta)) \cong \operatorname{\mathrm{Bl}}_{\alpha(n,\chi_P)}(P) \oplus \bigoplus_{i=1}^{n} \operatorname{\mathrm{Bl}}(K)(\xi_m^{\chi_{i}(q_Q(\mu_K^{-w}\eta))}t^{w/n}).\end{align*}$$
Case 2. If w is not divisible by n, then (4.22) and Theorem 3.11 imply that
![]() $\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(P(K,\eta ))$
is Witt equivalent to
$\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(P(K,\eta ))$
is Witt equivalent to
 $$\begin{align*}\operatorname{\mathrm{Bl}}_{\alpha(n,\chi_{P})}(P) \oplus \bigoplus_{i=1}^{h} \operatorname{\mathrm{Bl}}_{\alpha_K(n/h,\chi_{i})}(K)(\xi_m^{\chi_{i}(q_Q(\mu_K^{-w}\eta))}t^{w/h}).\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Bl}}_{\alpha(n,\chi_{P})}(P) \oplus \bigoplus_{i=1}^{h} \operatorname{\mathrm{Bl}}_{\alpha_K(n/h,\chi_{i})}(K)(\xi_m^{\chi_{i}(q_Q(\mu_K^{-w}\eta))}t^{w/h}).\end{align*}$$
Next, we assume that
![]() $w=0$
. As the abelianization map
$w=0$
. As the abelianization map
![]() $\phi \colon H_1(M_{P(K,\eta )};\mathbb {Z}) \to \mathbb {Z}$
restricts to the zero map on
$\phi \colon H_1(M_{P(K,\eta )};\mathbb {Z}) \to \mathbb {Z}$
restricts to the zero map on
![]() $H_1(M_K;\mathbb {Z})$
, it follows that
$H_1(M_K;\mathbb {Z})$
, it follows that
![]() $\alpha (n,\chi )_K$
is abelian. More precisely,
$\alpha (n,\chi )_K$
is abelian. More precisely,
![]() $\alpha (n,\chi )_{K} \cong \bigoplus _{i=1}^{n} \xi _m^{\chi _i}$
, where
$\alpha (n,\chi )_{K} \cong \bigoplus _{i=1}^{n} \xi _m^{\chi _i}$
, where
![]() $\xi _m^{\chi _i}$
is understood as the character mapping
$\xi _m^{\chi _i}$
is understood as the character mapping
![]() $\mu _K$
to
$\mu _K$
to
![]() $\xi _m^{\chi _i(q_Q(\eta ))}$
. As a consequence, we obtain the isomorphism
$\xi _m^{\chi _i(q_Q(\eta ))}$
. As a consequence, we obtain the isomorphism
 $$ \begin{align*}H_{\ast}(M_{K};{\mathbb{C}}[t^{\pm 1}]^{n}_{\alpha(n,\chi)}) \cong \bigoplus_{i=1}^n H_{1}(M_{K};{\mathbb{C}}[t^{\pm 1}]_{\xi_m^{\chi_i}})\cong \bigoplus_{i=1}^n H_{1}(M_{K};\mathbb{C}_{\xi_m^{\chi_i}}) \otimes_{\mathbb{C}}{\mathbb{C}}[t^{\pm 1}].\end{align*} $$
$$ \begin{align*}H_{\ast}(M_{K};{\mathbb{C}}[t^{\pm 1}]^{n}_{\alpha(n,\chi)}) \cong \bigoplus_{i=1}^n H_{1}(M_{K};{\mathbb{C}}[t^{\pm 1}]_{\xi_m^{\chi_i}})\cong \bigoplus_{i=1}^n H_{1}(M_{K};\mathbb{C}_{\xi_m^{\chi_i}}) \otimes_{\mathbb{C}}{\mathbb{C}}[t^{\pm 1}].\end{align*} $$
The dimension of
![]() $H_{1}(M_{K};\mathbb {C}_{\xi _m^{\chi _i}}) $
is equal to
$H_{1}(M_{K};\mathbb {C}_{\xi _m^{\chi _i}}) $
is equal to
![]() $\eta _K(\xi _m^{\chi _i(q_Q(\eta ))})$
, the nullity of K evaluated at the unit complex number
$\eta _K(\xi _m^{\chi _i(q_Q(\eta ))})$
, the nullity of K evaluated at the unit complex number
![]() $\xi _m^{\chi _i(q_Q(\eta ))}=\xi _m^{\chi (t_Q^{i-1}q_Q(\eta ))}$
. This value is non-zero if and only if the Alexander polynomial satisfies
$\xi _m^{\chi _i(q_Q(\eta ))}=\xi _m^{\chi (t_Q^{i-1}q_Q(\eta ))}$
. This value is non-zero if and only if the Alexander polynomial satisfies
![]() $\Delta _K(\xi _m^{\chi (t_Q^{i-1}q_Q(\eta ))})=0$
. Since the character
$\Delta _K(\xi _m^{\chi (t_Q^{i-1}q_Q(\eta ))})=0$
. Since the character
![]() $\chi $
has prime power order, this can never happen [Reference Friedl19, proof of Proposition 3.3], and we therefore deduce that
$\chi $
has prime power order, this can never happen [Reference Friedl19, proof of Proposition 3.3], and we therefore deduce that
![]() $H_{\ast }(M_{K};{\mathbb {C}}[t^{\pm 1}]^{n}_{\alpha (n,\chi )})=~0.$
Applying Corollary 3.15 now provides the desired isometry:
$H_{\ast }(M_{K};{\mathbb {C}}[t^{\pm 1}]^{n}_{\alpha (n,\chi )})=~0.$
Applying Corollary 3.15 now provides the desired isometry:
This concludes the proof of the theorem.
Appendix A Shapiro’s lemma and twisted Blanchfield forms
The goal of this appendix is to prove Corollary 4.6 which relates the Blanchfield form of the cover
![]() $\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(M_n)$
to the metabelian Blanchfield form
$\operatorname {\mathrm {Bl}}_{\alpha \times \chi }(M_n)$
to the metabelian Blanchfield form
![]() $\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(K)$
. Since the proof is somewhat technical, we will first need to collect a certain number of preliminaries. Namely, in Subsections A.1, A.2 and A.3, we respectively recall some facts about Bockstein homomorphisms, evaluation maps in twisted (co)homology, and (co)induced modules. Finally, Subsection A.4 proves Proposition A.11 which is a generalization of Corollary 4.6.
$\operatorname {\mathrm {Bl}}_{\alpha (n,\chi )}(K)$
. Since the proof is somewhat technical, we will first need to collect a certain number of preliminaries. Namely, in Subsections A.1, A.2 and A.3, we respectively recall some facts about Bockstein homomorphisms, evaluation maps in twisted (co)homology, and (co)induced modules. Finally, Subsection A.4 proves Proposition A.11 which is a generalization of Corollary 4.6.
A.1 Twisted homology: functoriality and Bocksteins
First, we briefly recall the sense in which twisted (co)homology is functorial. We then prove a lemma about the functoriality of Bockstein homomorphisms in twisted homology.
Construction A.1. Fix a ring R, path-connected CW complexes
![]() $X,Y$
, a
$X,Y$
, a
![]() $(R,\mathbb {Z}[\pi _1(X)])$
-bimodule M and an
$(R,\mathbb {Z}[\pi _1(X)])$
-bimodule M and an
![]() $(R,\mathbb {Z}[\pi _1(Y)])$
-bimodule N.
$(R,\mathbb {Z}[\pi _1(Y)])$
-bimodule N.
-
• Given a map
 $f \colon X \to Y$
, endow N with the right
$f \colon X \to Y$
, endow N with the right
 $\mathbb {Z}[\pi _1(X)]$
-module structure obtained by pulling back the right
$\mathbb {Z}[\pi _1(X)]$
-module structure obtained by pulling back the right
 $\mathbb {Z}[\pi _1(Y)]$
-module structure via the induced map
$\mathbb {Z}[\pi _1(Y)]$
-module structure via the induced map
 $f_{\ast } \colon \pi _{1}(X) \to \pi _{1}(Y)$
. Now f and a
$f_{\ast } \colon \pi _{1}(X) \to \pi _{1}(Y)$
. Now f and a
 $(R,\mathbb {Z}[\pi _1(X)])$
-bimodule map
$(R,\mathbb {Z}[\pi _1(X)])$
-bimodule map
 $\alpha \colon M \to N$
induce an R-linear map To see this, one verifies that
$\alpha \colon M \to N$
induce an R-linear map To see this, one verifies that $$ \begin{align*}(f,\alpha)_* \colon H_*(X;M) \to H_*(Y;N).\end{align*} $$
$$ \begin{align*}(f,\alpha)_* \colon H_*(X;M) \to H_*(Y;N).\end{align*} $$
 $\alpha $
and f induce well-defined chain maps where
$\alpha $
and f induce well-defined chain maps where $$\begin{align*}M \otimes_{\mathbb{Z}[\pi_{1}](X)} C_{\ast}(\widetilde{X}) \xrightarrow{\alpha \otimes \operatorname{id}} N \otimes_{\mathbb{Z}[\pi_{1}(X)]} C_{\ast}(\widetilde{X}) \xrightarrow{\operatorname{id} \otimes \widetilde{f}} N \otimes_{\mathbb{Z}[\pi_{1}(Y)]} C_{\ast}(\widetilde{Y}),\end{align*}$$
$$\begin{align*}M \otimes_{\mathbb{Z}[\pi_{1}](X)} C_{\ast}(\widetilde{X}) \xrightarrow{\alpha \otimes \operatorname{id}} N \otimes_{\mathbb{Z}[\pi_{1}(X)]} C_{\ast}(\widetilde{X}) \xrightarrow{\operatorname{id} \otimes \widetilde{f}} N \otimes_{\mathbb{Z}[\pi_{1}(Y)]} C_{\ast}(\widetilde{Y}),\end{align*}$$
 $\widetilde {f} \colon \widetilde {X} \to \widetilde {Y}$
is the lift of f to universal covers.
$\widetilde {f} \colon \widetilde {X} \to \widetilde {Y}$
is the lift of f to universal covers.
-
• In a similar manner, if
 $\alpha \colon N \to M$
is a homomorphism of
$\alpha \colon N \to M$
is a homomorphism of
 $(R,\mathbb {Z}[\pi _{1}(X)])$
-bimodules, we obtain an R-linear map on cohomology induced by the composition of cochain maps
$(R,\mathbb {Z}[\pi _{1}(X)])$
-bimodules, we obtain an R-linear map on cohomology induced by the composition of cochain maps $$\begin{align*}(f,\alpha)^{\ast} \colon H^{\ast}(Y;N) \to H^{\ast}(X,M)\end{align*}$$
$$\begin{align*}(f,\alpha)^{\ast} \colon H^{\ast}(Y;N) \to H^{\ast}(X,M)\end{align*}$$
 $$ \begin{align*} \operatorname{\mathrm{Hom}}_{\text{right-}\mathbb{Z}[\pi_1(Y)]}(C_*(\widetilde{Y})^\#,N) & \xrightarrow{\hom(\widetilde{f},\operatorname{id}_{N})} \operatorname{\mathrm{Hom}}_{\text{right-}\mathbb{Z}[\pi_1(X)]}(C_*(\widetilde{X})^\#,N) \\ & \xrightarrow{\hom(\operatorname{id},\alpha)} \operatorname{\mathrm{Hom}}_{\text{right-}\mathbb{Z}[\pi_1(X)]}(C_*(\widetilde{X})^\#,M). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Hom}}_{\text{right-}\mathbb{Z}[\pi_1(Y)]}(C_*(\widetilde{Y})^\#,N) & \xrightarrow{\hom(\widetilde{f},\operatorname{id}_{N})} \operatorname{\mathrm{Hom}}_{\text{right-}\mathbb{Z}[\pi_1(X)]}(C_*(\widetilde{X})^\#,N) \\ & \xrightarrow{\hom(\operatorname{id},\alpha)} \operatorname{\mathrm{Hom}}_{\text{right-}\mathbb{Z}[\pi_1(X)]}(C_*(\widetilde{X})^\#,M). \end{align*} $$
The definition of the Blanchfield form involves a Bockstein homomorphism. It should therefore not surprise the reader that to relate the Blanchfield pairing of the cover to the metabelian Blanchfield form, we need to know how Bocksteins interact with induced maps. To this effect, recall that if we are given an exact sequence
of
![]() $(R,\mathbb {Z}[\pi _{1}(X)])$
-bimodules, then, for any
$(R,\mathbb {Z}[\pi _{1}(X)])$
-bimodules, then, for any
![]() $k \geq 0$
, there are associated Bockstein homomorphisms
$k \geq 0$
, there are associated Bockstein homomorphisms
The following lemma shows that these Bockstein homomorphisms are natural.
Lemma A.2. Let
![]() $f \colon X \to Y$
be a map of path-connected CW complexes. Suppose that we are given a commutative diagram
$f \colon X \to Y$
be a map of path-connected CW complexes. Suppose that we are given a commutative diagram

where the first row is an exact sequence of
![]() $(R,\mathbb {Z}[\pi _{1}(X)])$
-bimodules, the second row is an exact sequence of
$(R,\mathbb {Z}[\pi _{1}(X)])$
-bimodules, the second row is an exact sequence of
![]() $(R,\mathbb {Z}[\pi _{1}(Y)])$
-bimodules and the maps
$(R,\mathbb {Z}[\pi _{1}(Y)])$
-bimodules and the maps
![]() $\alpha _{i}$
, for
$\alpha _{i}$
, for
![]() $i=1,2,3$
, are homomorphisms of
$i=1,2,3$
, are homomorphisms of
![]() $(R,\mathbb {Z}[\pi _{1}(X)])$
-bimodules. Recall that
$(R,\mathbb {Z}[\pi _{1}(X)])$
-bimodules. Recall that
![]() $N_{i}$
, for
$N_{i}$
, for
![]() $i=1,2,3$
, is equipped with a right action of
$i=1,2,3$
, is equipped with a right action of
![]() $\mathbb {Z}[\pi _{1}(X)]$
by pulling back the right action of
$\mathbb {Z}[\pi _{1}(X)]$
by pulling back the right action of
![]() $\mathbb {Z}[\pi _{1}(Y)]$
via the induced map
$\mathbb {Z}[\pi _{1}(Y)]$
via the induced map
![]() $f_{\ast } \colon \pi _{1}(X) \to \pi _{1}(Y)$
.
$f_{\ast } \colon \pi _{1}(X) \to \pi _{1}(Y)$
.
For any
![]() $k \geq 0$
, the following diagram is commutative:
$k \geq 0$
, the following diagram is commutative:

where the maps denoted by
![]() $BS$
are the respective Bockstein homomorphisms associated to the exact sequences in (A.1).
$BS$
are the respective Bockstein homomorphisms associated to the exact sequences in (A.1).
Proof. The reader can readily verify that the following diagram of chain complexes of left R-modules is commutative:

The lemma now follows by taking induced maps on (co)homology.
A.2 The evaluation map: detailed definition and naturality
We recall some details regarding the evaluation map
![]() $\operatorname {\mathrm {ev}}$
on twisted cohomology that was mentioned in Subsection 2.1. We then prove that this evaluation map is natural.
$\operatorname {\mathrm {ev}}$
on twisted cohomology that was mentioned in Subsection 2.1. We then prove that this evaluation map is natural.
Fix a CW pair
![]() $(X,A)$
and a ring R that is endowed with an involution
$(X,A)$
and a ring R that is endowed with an involution
![]() $x \mapsto x^\#$
. Let M and
$x \mapsto x^\#$
. Let M and
![]() $M'$
be
$M'$
be
![]() $(R,\mathbb {Z}[\pi _1(X)])$
-bimodules and let S be an
$(R,\mathbb {Z}[\pi _1(X)])$
-bimodules and let S be an
![]() $(R,R)$
-bimodule. Furthermore, let
$(R,R)$
-bimodule. Furthermore, let
![]() $\langle -,-\rangle \colon M' \times M \to S$
be a non-singular
$\langle -,-\rangle \colon M' \times M \to S$
be a non-singular
![]() $\pi _1(X)$
-invariant sesquilinear pairing.
$\pi _1(X)$
-invariant sesquilinear pairing.
Construction A.3. We construct the evaluation
![]() $\operatorname {\mathrm {ev}} \colon H^i(X,A;M) \to \operatorname {\mathrm {Hom}}_{\text {left-}R}(H_{i}(X,A; M'),S)^\#$
.
$\operatorname {\mathrm {ev}} \colon H^i(X,A;M) \to \operatorname {\mathrm {Hom}}_{\text {left-}R}(H_{i}(X,A; M'),S)^\#$
.
The evaluation map can be defined in two steps. First, the non-singularity of the pairing
![]() $\langle -,-\rangle $
implies that the following map is an isomorphism of cochain complexes of left R-modules:
$\langle -,-\rangle $
implies that the following map is an isomorphism of cochain complexes of left R-modules:
 $$ \begin{align*} \kappa \colon \operatorname{\mathrm{Hom}}_{\text{right-}\mathbb{Z}[\pi_{1}(X)]}(C_{\ast}(X,A)^\#,M) &\to \operatorname{\mathrm{Hom}}_{\text{left-}R}(M' \otimes C_{\ast}(X,A),S)^\#, \\ f &\mapsto \left((m' \otimes \sigma) \mapsto \langle m',f(\sigma) \rangle \right). \end{align*} $$
$$ \begin{align*} \kappa \colon \operatorname{\mathrm{Hom}}_{\text{right-}\mathbb{Z}[\pi_{1}(X)]}(C_{\ast}(X,A)^\#,M) &\to \operatorname{\mathrm{Hom}}_{\text{left-}R}(M' \otimes C_{\ast}(X,A),S)^\#, \\ f &\mapsto \left((m' \otimes \sigma) \mapsto \langle m',f(\sigma) \rangle \right). \end{align*} $$
Second, evaluating cocycles on homology classes yields a homomorphism of left R-modules
Finally, the evaluation map
![]() $\operatorname {\mathrm {ev}}$
, which is also left R-linear, is obtained by composing
$\operatorname {\mathrm {ev}}$
, which is also left R-linear, is obtained by composing
![]() $\kappa $
with E:
$\kappa $
with E:
Note that E is the edge homomorphism in the universal coefficient spectral squence.
We now prove a naturality statement for this evaluation map. While this result also holds for pairs, we only state it for absolute homology since this is all we require in the sequel.
Lemma A.4. Let
![]() $X,Y$
be path-connected CW-complexes. Let M,
$X,Y$
be path-connected CW-complexes. Let M,
![]() $M'$
be
$M'$
be
![]() $(R,\mathbb {Z}[\pi _{1}(X)])$
-bimodules, let N,
$(R,\mathbb {Z}[\pi _{1}(X)])$
-bimodules, let N,
![]() $N'$
be
$N'$
be
![]() $(R,\mathbb {Z}[\pi _{1}(Y)])$
-bimodules and let
$(R,\mathbb {Z}[\pi _{1}(Y)])$
-bimodules and let
![]() $S,T$
be
$S,T$
be
![]() $(R,R)$
-bimodules. Suppose also that we are given non-singular
$(R,R)$
-bimodules. Suppose also that we are given non-singular
![]() $\pi _1(X)$
-equivariant (resp.
$\pi _1(X)$
-equivariant (resp.
![]() $\pi _1(Y)$
-equivariant) sesquilinear pairings
$\pi _1(Y)$
-equivariant) sesquilinear pairings
Recall that we can equip N and
![]() $N'$
with a right action of
$N'$
with a right action of
![]() $\mathbb {Z}[\pi _{1}(X)]$
by pulling back the right
$\mathbb {Z}[\pi _{1}(X)]$
by pulling back the right
![]() $\mathbb {Z}[\pi _{1}(Y)]$
-action by the induced homomorphism
$\mathbb {Z}[\pi _{1}(Y)]$
-action by the induced homomorphism
![]() $f_{\ast } \colon \pi _{1}(X) \to \pi _{1}(Y)$
. If there are
$f_{\ast } \colon \pi _{1}(X) \to \pi _{1}(Y)$
. If there are
![]() $(R,\mathbb {Z}[\pi _{1}(X)])$
-linear maps
$(R,\mathbb {Z}[\pi _{1}(X)])$
-linear maps
![]() $\alpha \colon N \to M$
and
$\alpha \colon N \to M$
and
![]() $ \alpha ' \colon M' \to N' $
as well as an
$ \alpha ' \colon M' \to N' $
as well as an
![]() $(R,R)$
-linear map
$(R,R)$
-linear map
![]() $\beta \colon T \to S$
such that for all
$\beta \colon T \to S$
such that for all
![]() $m' \in M'$
and
$m' \in M'$
and
![]() $n \in N$
$n \in N$
then the following diagram of left R-modules commutes:

Proof. Naturality of the universal coefficient spectral sequence implies that it is sufficient to prove that the following diagram of cochain complexes of left R-modules is commutative:

Starting with a
![]() $\phi \in \operatorname {\mathrm {Hom}}_{\text {right-}\mathbb {Z}[\pi _1(Y)]}(C_{\ast }(\widetilde {Y})^\#,N)$
in the lower left corner of this diagram and going up, we have
$\phi \in \operatorname {\mathrm {Hom}}_{\text {right-}\mathbb {Z}[\pi _1(Y)]}(C_{\ast }(\widetilde {Y})^\#,N)$
in the lower left corner of this diagram and going up, we have
![]() $(f,\alpha )(\phi ) = \alpha \circ \phi \circ f$
. Similarly, if we start with
$(f,\alpha )(\phi ) = \alpha \circ \phi \circ f$
. Similarly, if we start with
![]() $\phi \in \operatorname {\mathrm {Hom}}_{\text {left-}R}(N' \otimes _{\mathbb {Z}[\pi _1(Y)]} C_{\ast }(\widetilde {Y}),T)^\#$
in the lower right corner and go up, then we obtain
$\phi \in \operatorname {\mathrm {Hom}}_{\text {left-}R}(N' \otimes _{\mathbb {Z}[\pi _1(Y)]} C_{\ast }(\widetilde {Y}),T)^\#$
in the lower right corner and go up, then we obtain
With these observations at hand, starting with
![]() $\phi \in \operatorname {\mathrm {Hom}}_{\text {right-}\mathbb {Z}[\pi _1(Y)]}(C_{\ast }(\widetilde {Y})^\#,N)$
in the lower left corner, the up-right and right-up paths of the diagram respectively yield
$\phi \in \operatorname {\mathrm {Hom}}_{\text {right-}\mathbb {Z}[\pi _1(Y)]}(C_{\ast }(\widetilde {Y})^\#,N)$
in the lower left corner, the up-right and right-up paths of the diagram respectively yield
 $$ \begin{align*} (\kappa \circ (f,\alpha))(\phi)(m' \otimes \sigma) &= \langle m', (\alpha \circ \phi \circ f)(\sigma) \rangle_{X}, \\ (\operatorname{\mathrm{Hom}}((f,\alpha'),\beta) \circ \kappa)(\phi)(m' \otimes \sigma) &= \beta \left( \langle \alpha'(m'), (\phi \circ f)(\sigma) \rangle_{Y} \right), \end{align*} $$
$$ \begin{align*} (\kappa \circ (f,\alpha))(\phi)(m' \otimes \sigma) &= \langle m', (\alpha \circ \phi \circ f)(\sigma) \rangle_{X}, \\ (\operatorname{\mathrm{Hom}}((f,\alpha'),\beta) \circ \kappa)(\phi)(m' \otimes \sigma) &= \beta \left( \langle \alpha'(m'), (\phi \circ f)(\sigma) \rangle_{Y} \right), \end{align*} $$
for all
![]() $m' \in M'$
and all
$m' \in M'$
and all
![]() $\sigma \in C_{\ast }(\widetilde {X})$
. Using the hypothesis of the lemma, both quantities are equal, and hence, the required commutativity follows. This concludes the proof of the lemma.
$\sigma \in C_{\ast }(\widetilde {X})$
. Using the hypothesis of the lemma, both quantities are equal, and hence, the required commutativity follows. This concludes the proof of the lemma.
A.3 Induced and coinduced representations
We now need to introduce one last ingredient before delving into the proof of Corollary 4.6. Namely, we recall some basic facts about the induction and coinduction functors as these will play a role in expliciting the isometry between the Blanchfield form in the cover and the metabelian Blanchfield form. As in the previous sections, we fix a ring R with involution.
Definition A.5. Let G be a group and let H be a subgroup of G. For any
![]() $(R,\mathbb {Z}[H])$
-bimodule M, the induced
$(R,\mathbb {Z}[H])$
-bimodule M, the induced
![]() $(R,\mathbb {Z}[G])$
-bimodule refers to the
$(R,\mathbb {Z}[G])$
-bimodule refers to the
![]() $(R,\mathbb {Z}[G])$
-bimodule
$(R,\mathbb {Z}[G])$
-bimodule
Similarly, the coinduced
![]() $(R,\mathbb {Z}[G])$
-bimodule refers to
$(R,\mathbb {Z}[G])$
-bimodule refers to
The structure of a
![]() $(R,\mathbb {Z}[G])$
-bimodule on
$(R,\mathbb {Z}[G])$
-bimodule on
![]() $\operatorname {Coind}^{G}_{H}(M)$
is given as follows: for
$\operatorname {Coind}^{G}_{H}(M)$
is given as follows: for
![]() $r \in R$
,
$r \in R$
,
![]() $f \in \operatorname {Coind}^{G}_{H}(M)$
, and
$f \in \operatorname {Coind}^{G}_{H}(M)$
, and
![]() $x,y \in \mathbb {Z}[G]$
,
$x,y \in \mathbb {Z}[G]$
,
Example A.6. Consider a group G and a subgroup
![]() $H \leq G$
of finite index n. Given a commutative ring R, we use induction to explain how a representation
$H \leq G$
of finite index n. Given a commutative ring R, we use induction to explain how a representation
![]() $\beta \colon H \to GL_d(R)$
induces a representation
$\beta \colon H \to GL_d(R)$
induces a representation
First, some setup. Let
![]() $g_{1}, g_{2}, \ldots , g_{n}$
be representatives of cosets
$g_{1}, g_{2}, \ldots , g_{n}$
be representatives of cosets
![]() $H \backslash G$
. As a left
$H \backslash G$
. As a left
![]() $\mathbb {Z}[H]$
-module,
$\mathbb {Z}[H]$
-module,
![]() $\mathbb {Z}[G]$
is a free module of rank n and admits a decomposition
$\mathbb {Z}[G]$
is a free module of rank n and admits a decomposition
 $$ \begin{align} \mathbb{Z}[G] = \bigoplus_{i=1}^{n} \mathbb{Z}[Hg_{i}]. \end{align} $$
$$ \begin{align} \mathbb{Z}[G] = \bigoplus_{i=1}^{n} \mathbb{Z}[Hg_{i}]. \end{align} $$
Hence, the set
![]() $ \lbrace 1_{G}=g_{1},g_{2},\ldots ,g_{n} \rbrace $
is a
$ \lbrace 1_{G}=g_{1},g_{2},\ldots ,g_{n} \rbrace $
is a
![]() $\mathbb {Z}[H]$
-basis of
$\mathbb {Z}[H]$
-basis of
![]() $\mathbb {Z}[G]$
treated as a left
$\mathbb {Z}[G]$
treated as a left
![]() $\mathbb {Z}[H]$
-module. Observe that the above decomposition does not depend on the particular choice of coset representatives.
$\mathbb {Z}[H]$
-module. Observe that the above decomposition does not depend on the particular choice of coset representatives.
Next, we describe the representation
![]() $\operatorname {Ind}^{G}_{H}(\beta )$
. The representation
$\operatorname {Ind}^{G}_{H}(\beta )$
. The representation
![]() $\beta $
equips the free R-module
$\beta $
equips the free R-module
![]() $R^{d}$
with the right action from H; hence, it becomes a
$R^{d}$
with the right action from H; hence, it becomes a
![]() $(R,\mathbb {Z}[H])$
-bimodule. Using (A.3), the induced
$(R,\mathbb {Z}[H])$
-bimodule. Using (A.3), the induced
![]() $(R,\mathbb {Z}[G])$
-bimodule
$(R,\mathbb {Z}[G])$
-bimodule
![]() $\operatorname {Ind}^{G}_{H}(R^{d}_{\beta })$
can be decomposed as
$\operatorname {Ind}^{G}_{H}(R^{d}_{\beta })$
can be decomposed as
 $$ \begin{align} \operatorname{Ind}^{G}_{H}(R^{d}_{\beta}) = R^{d}_{\beta} \otimes_{\mathbb{Z}[H]} \mathbb{Z}[G] = \bigoplus_{i=1}^{n} R^{d}_{\beta} \otimes_{\mathbb{Z}[H]} \mathbb{Z}[Hg_{i}]. \end{align} $$
$$ \begin{align} \operatorname{Ind}^{G}_{H}(R^{d}_{\beta}) = R^{d}_{\beta} \otimes_{\mathbb{Z}[H]} \mathbb{Z}[G] = \bigoplus_{i=1}^{n} R^{d}_{\beta} \otimes_{\mathbb{Z}[H]} \mathbb{Z}[Hg_{i}]. \end{align} $$
In order to shorten the notation, we set
![]() $R^{d}_{\beta } \otimes g_{i} := R^{d}_{\beta } \otimes _{\mathbb {Z}[H]} \mathbb {Z}[Hg_{i}]$
. Note that as a left R-module,
$R^{d}_{\beta } \otimes g_{i} := R^{d}_{\beta } \otimes _{\mathbb {Z}[H]} \mathbb {Z}[Hg_{i}]$
. Note that as a left R-module,
![]() $\operatorname {Ind}^{G}_{H}(R^{d}_{\beta })$
is free of rank
$\operatorname {Ind}^{G}_{H}(R^{d}_{\beta })$
is free of rank
![]() $nd$
. Since
$nd$
. Since
![]() $\operatorname {Ind}^{G}_{H}(R^{d}_{\beta }) \cong R^{dn}$
is a right
$\operatorname {Ind}^{G}_{H}(R^{d}_{\beta }) \cong R^{dn}$
is a right
![]() $\mathbb {Z}[G]$
-module, we therefore obtain the desired induced representation
$\mathbb {Z}[G]$
-module, we therefore obtain the desired induced representation
![]() $\alpha := \operatorname {Ind}^{G}_{H}(\beta ) \colon G \to GL_{dn}(R).$
$\alpha := \operatorname {Ind}^{G}_{H}(\beta ) \colon G \to GL_{dn}(R).$
Construction A.7. Given a group G, a finite index subgroup
![]() $H \leq G$
and a
$H \leq G$
and a
![]() $(R,\mathbb {Z}[H])$
-bimodule M, we construct a
$(R,\mathbb {Z}[H])$
-bimodule M, we construct a
![]() $(R,\mathbb {Z}[G])$
-linear map
$(R,\mathbb {Z}[G])$
-linear map
![]() $\overline {\phi } \colon \operatorname {Ind}^{G}_{H}(M) \to \operatorname {Coind}^{G}_{H}(M)$
.
$\overline {\phi } \colon \operatorname {Ind}^{G}_{H}(M) \to \operatorname {Coind}^{G}_{H}(M)$
.
First, we consider the following homomorphism of
![]() $(R,\mathbb {Z}[H])$
-bimodules:
$(R,\mathbb {Z}[H])$
-bimodules:
 $$\begin{align*}\phi \colon M \to \operatorname{Coind}^{G}_{H}(M), \quad \phi(m)(g) = \begin{cases} m \cdot g, & g \in H, \\ 0, & g \not\in H, \end{cases} \end{align*}$$
$$\begin{align*}\phi \colon M \to \operatorname{Coind}^{G}_{H}(M), \quad \phi(m)(g) = \begin{cases} m \cdot g, & g \in H, \\ 0, & g \not\in H, \end{cases} \end{align*}$$
where
![]() $m \in M$
and
$m \in M$
and
![]() $g \in G$
. We can uniquely extend
$g \in G$
. We can uniquely extend
![]() $\phi $
to a homomorphism of
$\phi $
to a homomorphism of
![]() $(R,\mathbb {Z}[G])$
-bimodules
$(R,\mathbb {Z}[G])$
-bimodules
The reader can check that
![]() $\overline {\phi }$
is natural in M (i.e. it is a component of a natural transformation of the induction and coinduction functors).
$\overline {\phi }$
is natural in M (i.e. it is a component of a natural transformation of the induction and coinduction functors).
The map
![]() $\overline {\phi }$
is known to be an isomorphism of
$\overline {\phi }$
is known to be an isomorphism of
![]() $(R,\mathbb {Z}[G])$
-bimodules [Reference Brown5, Proposition III.5.9], but we describe the inverse explicitly when G is a finite group as we will need it in the sequel.
$(R,\mathbb {Z}[G])$
-bimodules [Reference Brown5, Proposition III.5.9], but we describe the inverse explicitly when G is a finite group as we will need it in the sequel.
Lemma A.8. Given a group G, a finite index subgroup
![]() $H \leq G$
and a
$H \leq G$
and a
![]() $(R,\mathbb {Z}[H])$
-bimodule M, the
$(R,\mathbb {Z}[H])$
-bimodule M, the
![]() $(R,\mathbb {Z}[G])$
-linear map
$(R,\mathbb {Z}[G])$
-linear map
![]() $\overline {\phi }$
from Construction A.7 defines a natural isomorphism of
$\overline {\phi }$
from Construction A.7 defines a natural isomorphism of
![]() $(R,\mathbb {Z}[G])$
-bimodules:
$(R,\mathbb {Z}[G])$
-bimodules:
Proof. The reader can check that the inverse of
![]() $\overline {\phi }$
is given by the formula
$\overline {\phi }$
is given by the formula
 $$ \begin{align} \overline{\psi} \colon \operatorname{Coind}^{G}_{H}(M) \to \operatorname{Ind}^{G}_{H}(M), \quad \overline{\psi}(f) = \sum_{g \in H \backslash G} f(g^{-1}) \otimes g. \end{align} $$
$$ \begin{align} \overline{\psi} \colon \operatorname{Coind}^{G}_{H}(M) \to \operatorname{Ind}^{G}_{H}(M), \quad \overline{\psi}(f) = \sum_{g \in H \backslash G} f(g^{-1}) \otimes g. \end{align} $$
Here, the notation
![]() $g \in H \backslash G$
means that we are summing over coset representatives of
$g \in H \backslash G$
means that we are summing over coset representatives of
![]() $H \backslash G$
. One readily verifies that
$H \backslash G$
. One readily verifies that
![]() $\overline {\psi }$
does not depend on the specific choice of representatives.
$\overline {\psi }$
does not depend on the specific choice of representatives.
Next, we introduce the maps that we will use to construct the isometry between the Blanchfield form of the cover and the metabelian Blanchfield form. Fix a
![]() $(R,\mathbb {Z}[H])$
-bimodule M and consider the following maps of
$(R,\mathbb {Z}[H])$
-bimodule M and consider the following maps of
![]() $(R,\mathbb {Z}[H])$
-bimodules:
$(R,\mathbb {Z}[H])$
-bimodules:
 $$ \begin{align} i^{G}_{H}(M) &\colon M \to \operatorname{Ind}^{G}_{H}(M), \quad M \owns m \mapsto m \otimes 1_{G} \in \operatorname{Ind}^{G}_{H}(M), \\ p^{G}_{H}(M) &\colon \operatorname{Coind}^{G}_{H}(M) \to M, \quad f \in \operatorname{Coind}^{G}_{H}(M) \mapsto f(1). \nonumber \end{align} $$
$$ \begin{align} i^{G}_{H}(M) &\colon M \to \operatorname{Ind}^{G}_{H}(M), \quad M \owns m \mapsto m \otimes 1_{G} \in \operatorname{Ind}^{G}_{H}(M), \\ p^{G}_{H}(M) &\colon \operatorname{Coind}^{G}_{H}(M) \to M, \quad f \in \operatorname{Coind}^{G}_{H}(M) \mapsto f(1). \nonumber \end{align} $$
Using the decomposition (A.3), we can see that M embeds in
![]() $\operatorname {Ind}^{G}_{H}(M)$
as the
$\operatorname {Ind}^{G}_{H}(M)$
as the
![]() $(R,\mathbb {Z}[H])$
-subbimodule
$(R,\mathbb {Z}[H])$
-subbimodule
![]() $M \otimes 1_{G}$
and
$M \otimes 1_{G}$
and
![]() $i^{G}_{H}(M)$
denotes the inclusion. Here, we used the same notation for the subbimodule
$i^{G}_{H}(M)$
denotes the inclusion. Here, we used the same notation for the subbimodule
![]() $M \otimes 1_{G}$
as in Example A.6. Dually, if we apply the functor
$M \otimes 1_{G}$
as in Example A.6. Dually, if we apply the functor
![]() $\hom _{\text {right}-\mathbb {Z}[H]}((-),M)$
to the inclusion
$\hom _{\text {right}-\mathbb {Z}[H]}((-),M)$
to the inclusion
![]() $\mathbb {Z}[H] \subset \mathbb {Z}[G]$
from Example A.6, we obtain the map
$\mathbb {Z}[H] \subset \mathbb {Z}[G]$
from Example A.6, we obtain the map
![]() $p^{G}_{H}(M)$
.
$p^{G}_{H}(M)$
.
The next lemma uses
![]() $\overline {\phi }$
and the maps from (A.7) to make more explicit the isomorphism from Proposition 4.4.
$\overline {\phi }$
and the maps from (A.7) to make more explicit the isomorphism from Proposition 4.4.
Lemma A.9 (Shapiro’s Lemma)
Suppose that X is a path-connected CW-complex and that
![]() $q \colon Y \to X$
is a finite-sheeted covering with Y also path-connected. For any
$q \colon Y \to X$
is a finite-sheeted covering with Y also path-connected. For any
![]() $(R,\mathbb {Z}[\pi _{1}(Y)])$
-bimodule M, the following maps are isomorphisms of left R-modules:
$(R,\mathbb {Z}[\pi _{1}(Y)])$
-bimodule M, the following maps are isomorphisms of left R-modules:
Here, the maps
![]() $i^{G}_{H}(M)$
and
$i^{G}_{H}(M)$
and
![]() $p^{G}_{H}(M)$
were defined in (A.7), and the map
$p^{G}_{H}(M)$
were defined in (A.7), and the map
![]() $\overline {\psi }$
was defined in the proof of Lemma A.8.
$\overline {\psi }$
was defined in the proof of Lemma A.8.
Proof. First, observe that by [Reference Brown5, Proposition III.6.2] and [Reference Brown5, Exercise III.8.2], the maps
![]() $(q,i^{G}_{H}(M))$
and
$(q,i^{G}_{H}(M))$
and
![]() $(q,p^{G}_{H}(M))$
induce isomorphisms of left R-modules; hence, the first isomorphism follows. To obtain the second isomorphism, observe that the map
$(q,p^{G}_{H}(M))$
induce isomorphisms of left R-modules; hence, the first isomorphism follows. To obtain the second isomorphism, observe that the map
![]() $(q,p^{G}_{H}(M) \circ \overline {\psi })$
can be written as a composition
$(q,p^{G}_{H}(M) \circ \overline {\psi })$
can be written as a composition
The map
![]() $(\operatorname {id},\overline {\psi })$
is an isomorphism by Lemma A.8; hence, the lemma follows.
$(\operatorname {id},\overline {\psi })$
is an isomorphism by Lemma A.8; hence, the lemma follows.
Before we end this section, we make one more observation concerning the interaction between induced representations and the Hermitian pairings defined in Example 2.1. This observation will be used in the proof of Proposition A.11.
We recall the setup: we fix a commutative domain R with involution
![]() $r \mapsto r^{\#}$
and quotient field Q with the involution extended from R. Recall, from Example 2.1, that for any
$r \mapsto r^{\#}$
and quotient field Q with the involution extended from R. Recall, from Example 2.1, that for any
![]() $d>0$
, there are pairings
$d>0$
, there are pairings
We additionally fix a group G, a normal subroup
![]() $H \leq G$
of finite index n and coset representatives
$H \leq G$
of finite index n and coset representatives
![]() $1=g_{1},g_{2},\ldots ,g_{n}$
of
$1=g_{1},g_{2},\ldots ,g_{n}$
of
![]() $H \backslash G$
.
$H \backslash G$
.
Lemma A.10. Fix a unitary representation
![]() $\beta \colon H \to GL_{d}(R)$
. Under the identification
$\beta \colon H \to GL_{d}(R)$
. Under the identification
![]() $\operatorname {Ind}^{G}_{H}(R^{d}_{\beta }) \cong R^{nd}_{\alpha }$
from Example A.6, the pairing
$\operatorname {Ind}^{G}_{H}(R^{d}_{\beta }) \cong R^{nd}_{\alpha }$
from Example A.6, the pairing
![]() $\langle -,- \rangle _{nd}$
$\langle -,- \rangle _{nd}$
![]() $\colon (Q/R \otimes _R R^{nd}_\alpha ) \times R^{nd}_\alpha \to Q/R$
is G-equivariant, and furthermore, for any
$\colon (Q/R \otimes _R R^{nd}_\alpha ) \times R^{nd}_\alpha \to Q/R$
is G-equivariant, and furthermore, for any
![]() $x \in (Q/R \otimes _{R} R^{d}_{\beta })$
and
$x \in (Q/R \otimes _{R} R^{d}_{\beta })$
and
![]() $y \in R^{d}_{\beta }$
, we have
$y \in R^{d}_{\beta }$
, we have
 $$ \begin{align} \langle (q \otimes v) \otimes g_{i}, w \otimes g_{j} \rangle_{nd} = \begin{cases} \langle q \otimes v,w \rangle_{d}, & \text{if } i = j, \\ 0, & \text{otherwise}. \end{cases} \end{align} $$
$$ \begin{align} \langle (q \otimes v) \otimes g_{i}, w \otimes g_{j} \rangle_{nd} = \begin{cases} \langle q \otimes v,w \rangle_{d}, & \text{if } i = j, \\ 0, & \text{otherwise}. \end{cases} \end{align} $$
Proof. We first calculate the right-hand side of (A.8) and, more specifically,
![]() $ \langle q \otimes v,w \rangle _{d}$
. The unitarity of
$ \langle q \otimes v,w \rangle _{d}$
. The unitarity of
![]() $\beta $
guarantees that the pairing
$\beta $
guarantees that the pairing
![]() $\langle -,- \rangle _{d}$
is H-equivariant: for any
$\langle -,- \rangle _{d}$
is H-equivariant: for any
![]() $h \in H$
, any
$h \in H$
, any
![]() $q \in Q/R$
, and any
$q \in Q/R$
, and any
![]() $v,w \in R^{d}_\beta $
, we have
$v,w \in R^{d}_\beta $
, we have
 $$ \begin{align} \langle (q \otimes v) \cdot h, w \cdot h \rangle_{d} & = \langle (q \otimes v) \beta(h), w \beta(h) \rangle_{d} = \beta(h)(\beta(h)^\#)^T \langle q \otimes v, w \rangle_{d} \\ \nonumber &= \langle q \otimes v, w \rangle_{d}=q(vw^\#)^T. \end{align} $$
$$ \begin{align} \langle (q \otimes v) \cdot h, w \cdot h \rangle_{d} & = \langle (q \otimes v) \beta(h), w \beta(h) \rangle_{d} = \beta(h)(\beta(h)^\#)^T \langle q \otimes v, w \rangle_{d} \\ \nonumber &= \langle q \otimes v, w \rangle_{d}=q(vw^\#)^T. \end{align} $$
Now we will calculate the left-hand side of (A.8).
Next, we assert that under the identification
![]() $\operatorname {Ind}^{G}_{H}(R^{d}_{\beta }) \cong R^{nd}_{\alpha }$
from Example A.6 (specifically the direct sum decomposition from (A.4)), we have
$\operatorname {Ind}^{G}_{H}(R^{d}_{\beta }) \cong R^{nd}_{\alpha }$
from Example A.6 (specifically the direct sum decomposition from (A.4)), we have
 $$\begin{align*}\langle (q \otimes v) \otimes g_i,w \otimes g_j \rangle_{nd}= q( v \otimes g_{i}) (w \otimes g_{j})^{\# T} = \begin{cases} q(vw^{\# T})& \text{if } i=j, \\ 0& \text{otherwise}, \end{cases} \end{align*}$$
$$\begin{align*}\langle (q \otimes v) \otimes g_i,w \otimes g_j \rangle_{nd}= q( v \otimes g_{i}) (w \otimes g_{j})^{\# T} = \begin{cases} q(vw^{\# T})& \text{if } i=j, \\ 0& \text{otherwise}, \end{cases} \end{align*}$$
for any
![]() $v,w \in R^{d}$
and
$v,w \in R^{d}$
and
![]() $q \in Q/R$
. More precisely, this assertion follows from the fact that if
$q \in Q/R$
. More precisely, this assertion follows from the fact that if
![]() $e_{1},e_{2},\ldots ,e_{d}$
denotes the standard basis vectors of
$e_{1},e_{2},\ldots ,e_{d}$
denotes the standard basis vectors of
![]() $R^{d}$
, then the standard basis of
$R^{d}$
, then the standard basis of
![]() $R^{nd}$
is given by
$R^{nd}$
is given by
The formula (A.8) then follows from the assertion and (A.9). We leave it to the reader to verify that
![]() $\langle -,- \rangle _{nd}$
is G-equivariant.
$\langle -,- \rangle _{nd}$
is G-equivariant.
A.4 Proof of Corollary 4.6
We are now ready to prove the main statement of this appendix which will in particular imply Corollary 4.6 by taking
![]() $M=M_K$
.
$M=M_K$
.
Proposition A.11 (Shapiro’s Lemma for Blanchfield forms)
Let M be a closed, oriented, connected
![]() $3$
-manifold and let
$3$
-manifold and let
![]() $q \colon M_{n} \to M$
be an n-sheeted covering, where
$q \colon M_{n} \to M$
be an n-sheeted covering, where
![]() $M_{n}$
is connected. Suppose that
$M_{n}$
is connected. Suppose that
![]() $\beta \colon \pi _{1}(M_{n}) \to GL_{d}({\mathbb {F}}[t^{\pm 1}])$
is an acyclic representation and denote
$\beta \colon \pi _{1}(M_{n}) \to GL_{d}({\mathbb {F}}[t^{\pm 1}])$
is an acyclic representation and denote
![]() $\alpha = \operatorname {Ind}^{\pi _{1}(M)}_{\pi _{1}(M_n)}(\beta ) \colon \pi _{1}(M) \to GL_{nd}({\mathbb {F}}[t^{\pm 1}])$
; see Example A.6. The isomorphism
$\alpha = \operatorname {Ind}^{\pi _{1}(M)}_{\pi _{1}(M_n)}(\beta ) \colon \pi _{1}(M) \to GL_{nd}({\mathbb {F}}[t^{\pm 1}])$
; see Example A.6. The isomorphism
coming from Shapiro’s Lemma A.9 yields an isometry of Blanchfield forms
Proof. Throughout this proof, we set
![]() $G:=\pi _{1}(M)$
and
$G:=\pi _{1}(M)$
and
![]() $H:= \pi _{1}(M_{n})$
. Writing
$H:= \pi _{1}(M_{n})$
. Writing
![]() $\operatorname {\mathrm {Bl}}_\beta ^\bullet (M_n)$
and
$\operatorname {\mathrm {Bl}}_\beta ^\bullet (M_n)$
and
![]() $\operatorname {\mathrm {Bl}}_\alpha ^\bullet (M)$
for the adjoints of the Blanchfield pairings in the statement of the proposition, we must show that the following diagram commutes:
$\operatorname {\mathrm {Bl}}_\alpha ^\bullet (M)$
for the adjoints of the Blanchfield pairings in the statement of the proposition, we must show that the following diagram commutes:

In diagram (A.10), the upper horizontal isomorphism comes from Shapiro’s Lemma A.9, and the bottom horizontal isomorphism is defined as
In order to prove the commutativity of the above square, we rewrite it in a different form by expanding
![]() $\operatorname {\mathrm {Bl}}_\beta ^\bullet (M_n)$
and
$\operatorname {\mathrm {Bl}}_\beta ^\bullet (M_n)$
and
![]() $\operatorname {\mathrm {Bl}}_\alpha ^\bullet (M)$
; see diagram (A.12). In this diagram, the first three horizontal maps are the isomorphisms coming from Shapiro’s Lemma A.9, and in the bottom horizontal line, we used the notation (A.11). Furthermore, in diagram (A.12), we identified
$\operatorname {\mathrm {Bl}}_\alpha ^\bullet (M)$
; see diagram (A.12). In this diagram, the first three horizontal maps are the isomorphisms coming from Shapiro’s Lemma A.9, and in the bottom horizontal line, we used the notation (A.11). Furthermore, in diagram (A.12), we identified
![]() $\operatorname {Ind}^{G}_{H}({\mathbb {F}}[t^{\pm 1}]^{d}_{\beta }) = {\mathbb {F}}[t^{\pm 1}]^{nd}_{\alpha }$
, as in Example A.6:
$\operatorname {Ind}^{G}_{H}({\mathbb {F}}[t^{\pm 1}]^{d}_{\beta }) = {\mathbb {F}}[t^{\pm 1}]^{nd}_{\alpha }$
, as in Example A.6:

Since each of the horizontal maps in the diagram are isomorphisms, we deduce that the conclusion of the proposition is equivalent to the commutativity of the diagram in (A.12). We will now prove that each of the squares commutes, starting with the middle square before moving on to the upper square and concluding with the bottom square.
-
• The commutativity of the middle square is a direct consequence of the naturality of the Bockstein map from Lemma A.2.
-
• We prove the commutativity of the top square. First, we observe that this is equivalent to proving that the diagram in (A.13) commutes, where
 $[M] \in H_3(M)$
and
$[M] \in H_3(M)$
and
 $[M_{n}] \in H_3(M_{n})$
respectively denote the fundamental classes of M and
$[M_{n}] \in H_3(M_{n})$
respectively denote the fundamental classes of M and
 $M_{n}$
and
$M_{n}$
and
 $\overline {\psi }$
was defined in the proof Lemma A.8. (A.13)
$\overline {\psi }$
was defined in the proof Lemma A.8. (A.13)
The commutativity of the diagram in (A.13) will be established by a strenuous but direct computation. Fix
 $\eta \in \operatorname {\mathrm {Hom}}_{\text {right-}\mathbb {Z}[G]}(C_{2}(\widetilde {M})^\#,\operatorname {Coind}^{G}_{H}(\mathbb {F}[t^{\pm 1}]^{d}_{\beta }))$
representing a cohomology class in
$\eta \in \operatorname {\mathrm {Hom}}_{\text {right-}\mathbb {Z}[G]}(C_{2}(\widetilde {M})^\#,\operatorname {Coind}^{G}_{H}(\mathbb {F}[t^{\pm 1}]^{d}_{\beta }))$
representing a cohomology class in
 $H^{2}(M;\operatorname {Coind}^{G}_{H}({\mathbb {F}}[t^{\pm 1}]^{d}_{\beta }))$
(i.e., an element in the bottom right entry of the diagram). We will first compute the image of
$H^{2}(M;\operatorname {Coind}^{G}_{H}({\mathbb {F}}[t^{\pm 1}]^{d}_{\beta }))$
(i.e., an element in the bottom right entry of the diagram). We will first compute the image of
 $\eta $
under the left-up-right composition and then by the up-up composition.
$\eta $
under the left-up-right composition and then by the up-up composition.-
– We calculate the image of
 $\eta $
under the left-up-right composition in (A.13). In other words, we must calculate
$\eta $
under the left-up-right composition in (A.13). In other words, we must calculate
 $(q,i_H^G)\left ( \left ( (q,p^{G}_{H})(\eta ) \right ) \cap \xi _{M_{n}} \right )$
, where
$(q,i_H^G)\left ( \left ( (q,p^{G}_{H})(\eta ) \right ) \cap \xi _{M_{n}} \right )$
, where
 $\xi _{M_n} \in C_3(M_n)$
is a chain representing the fundamental class of
$\xi _{M_n} \in C_3(M_n)$
is a chain representing the fundamental class of
 $M_n$
that we will now describe. Indeed, we wish to pick this
$M_n$
that we will now describe. Indeed, we wish to pick this
 $\xi _{M_n}$
in terms of a chain representing the fundamental class
$\xi _{M_n}$
in terms of a chain representing the fundamental class
 $[M]$
of M. To achieve this, we let
$[M]$
of M. To achieve this, we let
 $\widetilde {M}$
be the universal covering of (both) M and
$\widetilde {M}$
be the universal covering of (both) M and
 $M_{n}$
and let
$M_{n}$
and let
 $1=g_{1},g_{2},\ldots ,g_{n}$
be coset representatives of
$1=g_{1},g_{2},\ldots ,g_{n}$
be coset representatives of
 $H \backslash G$
; observe that H is a normal subgroup of G; hence
$H \backslash G$
; observe that H is a normal subgroup of G; hence
 $g_{1},g_{2},\ldots ,g_{n}$
are also coset representatives for
$g_{1},g_{2},\ldots ,g_{n}$
are also coset representatives for
 $G / H$
. This way, if we choose a chain
$G / H$
. This way, if we choose a chain
 $\xi _{M} \in C_{3}(\widetilde {M})$
representing the fundamental class in
$\xi _{M} \in C_{3}(\widetilde {M})$
representing the fundamental class in
 $C_{3}(M) = \mathbb {Z} \otimes _{\mathbb {Z}[G]}C_{3}(\widetilde {M})$
, the chain
$C_{3}(M) = \mathbb {Z} \otimes _{\mathbb {Z}[G]}C_{3}(\widetilde {M})$
, the chain
 $\xi _{M_{n}} = \sum _{i=1}^{n} g_{i} \cdot \xi _{M}$
represents the fundamental class of
$\xi _{M_{n}} = \sum _{i=1}^{n} g_{i} \cdot \xi _{M}$
represents the fundamental class of
 $M_{n}$
in
$M_{n}$
in
 $C_{3}(M_{n}) = \mathbb {Z} \otimes _{\mathbb {Z}[H]} C_{3}(\widetilde {M})$
. Using this choice of
$C_{3}(M_{n}) = \mathbb {Z} \otimes _{\mathbb {Z}[H]} C_{3}(\widetilde {M})$
. Using this choice of
 $\xi _{M_n}$
, we obtain that For the next step in this calculation, recall that for any
$\xi _{M_n}$
, we obtain that For the next step in this calculation, recall that for any $$ \begin{align*}\left( (q,p^{G}_{H})(\eta) \right) \cap \xi_{M_{n}} = \sum_{i=1}^{n} ((q,p^{G}_{H})(\eta)) \cap (g_{i} \cdot \xi_{M}).\end{align*} $$
$$ \begin{align*}\left( (q,p^{G}_{H})(\eta) \right) \cap \xi_{M_{n}} = \sum_{i=1}^{n} ((q,p^{G}_{H})(\eta)) \cap (g_{i} \cdot \xi_{M}).\end{align*} $$
 $(R,\mathbb {Z}[G])$
-bimodule A, the cap product gives a chain map where, for
$(R,\mathbb {Z}[G])$
-bimodule A, the cap product gives a chain map where, for
 $\sigma \in C_{j}(\widetilde {M})$
,
$\sigma \in C_{j}(\widetilde {M})$
,  and
and  denote the front face and back face of
denote the front face and back face of
 $\sigma $
, respectively. For more details concerning the twisted cap product, refer to [Reference Conway and Nagel14, Section 2.3]. As a consequence, we obtain But now, by definition of the map
$\sigma $
, respectively. For more details concerning the twisted cap product, refer to [Reference Conway and Nagel14, Section 2.3]. As a consequence, we obtain But now, by definition of the map
 $p^{G}_{H}$
(see (A.7)), we have
$p^{G}_{H}$
(see (A.7)), we have
 $(q,p^{G}_{H})(\eta )(\sigma ) = \eta (\sigma )(1)$
for any
$(q,p^{G}_{H})(\eta )(\sigma ) = \eta (\sigma )(1)$
for any
 $\sigma \in C_{2}(\widetilde {M})$
. Using this, we obtain where the second equality follows from our discussion of the map
$\sigma \in C_{2}(\widetilde {M})$
. Using this, we obtain where the second equality follows from our discussion of the map
 $(q,p_H^G)$
, the third follows from the fact that
$(q,p_H^G)$
, the third follows from the fact that
 $\eta $
is right-
$\eta $
is right-
 $\mathbb {Z}[G]$
-linear and the last follows from the definition of the right action of
$\mathbb {Z}[G]$
-linear and the last follows from the definition of the right action of
 $\mathbb {Z}[G]$
on
$\mathbb {Z}[G]$
on
 $\operatorname {Coind}^{G}_{H}({\mathbb {F}}[t^{\pm 1}]^{d}_{\beta })$
; see (A.2).
$\operatorname {Coind}^{G}_{H}({\mathbb {F}}[t^{\pm 1}]^{d}_{\beta })$
; see (A.2).
Finally, using the definition of
 $(q,i_H^G)$
, we deduce that the image of
$(q,i_H^G)$
, we deduce that the image of
 $\eta $
under the left-up-right composition is given by (A.14)
$\eta $
under the left-up-right composition is given by (A.14)
-
– We show that the image of
 $\eta $
under the up-up composition in (A.13) – namely,
$\eta $
under the up-up composition in (A.13) – namely,
 $(\operatorname {id},\overline {\psi })(\eta ) \cap \xi _{M}$
agrees with (A.14). By definition of
$(\operatorname {id},\overline {\psi })(\eta ) \cap \xi _{M}$
agrees with (A.14). By definition of
 $\overline {\psi }$
(recall (A.6)), for any chain
$\overline {\psi }$
(recall (A.6)), for any chain
 $\sigma \in C_{2}(\widetilde {M})$
, we have Consequently, using the definition of the cap product, we deduce that the image of
$\sigma \in C_{2}(\widetilde {M})$
, we have Consequently, using the definition of the cap product, we deduce that the image of $$\begin{align*}(\operatorname{id},\overline{\psi})(\eta)(\sigma) = \sum_{i=1}^{n} \eta(\sigma)(g_{i}^{-1}) \otimes g_{i}.\end{align*}$$
$$\begin{align*}(\operatorname{id},\overline{\psi})(\eta)(\sigma) = \sum_{i=1}^{n} \eta(\sigma)(g_{i}^{-1}) \otimes g_{i}.\end{align*}$$
 $\eta $
under the up-up composition is given by (A.15)where in the last equality, we used the fact that the outer tensor product is taken over the ring
$\eta $
under the up-up composition is given by (A.15)where in the last equality, we used the fact that the outer tensor product is taken over the ring
 $\mathbb {Z}[G]$
.
$\mathbb {Z}[G]$
.
Comparing (A.14) with (A.15) shows that the diagram in (A.13) is commutative; hence, the second step of the proof is finished.
-
-
• We prove the commutativity of the bottom square in (A.12). In fact, by Lemma A.4 (which concerned the naturality of evaluation maps), it suffices to prove that
(A.16)for every $$ \begin{align} \langle x, (p^{G}_{H} \circ \overline{\phi})(y) \rangle_{d} = \langle i^{G}_{H}(x), y \rangle_{nd} \end{align} $$
$$ \begin{align} \langle x, (p^{G}_{H} \circ \overline{\phi})(y) \rangle_{d} = \langle i^{G}_{H}(x), y \rangle_{nd} \end{align} $$
 $x \in (\mathbb {F}(t) / {\mathbb {F}}[t^{\pm 1}])^{d}_{\beta }$
and every
$x \in (\mathbb {F}(t) / {\mathbb {F}}[t^{\pm 1}])^{d}_{\beta }$
and every
 $y \in {\mathbb {F}}[t^{\pm 1}]^{nd}_{\alpha }$
, where the pairings
$y \in {\mathbb {F}}[t^{\pm 1}]^{nd}_{\alpha }$
, where the pairings
 $\langle -,- \rangle _{d}$
and
$\langle -,- \rangle _{d}$
and
 $\langle -,- \rangle _{nd}$
were considered in Example A.10. Our plan is to expand the expression
$\langle -,- \rangle _{nd}$
were considered in Example A.10. Our plan is to expand the expression
 $ \langle x, (p^{G}_{H} \circ \overline {\phi })(y) \rangle _{d}$
.
$ \langle x, (p^{G}_{H} \circ \overline {\phi })(y) \rangle _{d}$
.
As a first step, we get a better grasp on the map
 $(p^{G}_{H} \circ \overline {\phi })$
. For that, recall that since
$(p^{G}_{H} \circ \overline {\phi })$
. For that, recall that since
 $1=g_{1}, g_{2}, \ldots , g_{n}$
are coset representative of
$1=g_{1}, g_{2}, \ldots , g_{n}$
are coset representative of
 $H \backslash G$
, we can write as in Example A.6 Observe that equations (A.5) and (A.7) imply that the map
$H \backslash G$
, we can write as in Example A.6 Observe that equations (A.5) and (A.7) imply that the map $$\begin{align*}\operatorname{Ind}^{G}_{H}({\mathbb{F}}[t^{\pm 1}]^{d}_{\beta}) = \bigoplus_{i=1}^{n} {\mathbb{F}}[t^{\pm 1}]^{d}_{\beta} \otimes g_{i} = {\mathbb{F}}[t^{\pm 1}]^{nd}_{\alpha}.\end{align*}$$
$$\begin{align*}\operatorname{Ind}^{G}_{H}({\mathbb{F}}[t^{\pm 1}]^{d}_{\beta}) = \bigoplus_{i=1}^{n} {\mathbb{F}}[t^{\pm 1}]^{d}_{\beta} \otimes g_{i} = {\mathbb{F}}[t^{\pm 1}]^{nd}_{\alpha}.\end{align*}$$
 $p^{G}_{H} \circ \overline {\phi } \colon {\mathbb {F}}[t^{\pm 1}]^{nd}_{\alpha } \to {\mathbb {F}}[t^{\pm 1}]^{d}_{\beta }$
is given by the formula where
$p^{G}_{H} \circ \overline {\phi } \colon {\mathbb {F}}[t^{\pm 1}]^{nd}_{\alpha } \to {\mathbb {F}}[t^{\pm 1}]^{d}_{\beta }$
is given by the formula where $$\begin{align*}p^{G}_{H}(v \otimes g_{i}) = \begin{cases} v& \text{if } i=1, \\ 0& \text{otherwise}, \end{cases} \end{align*}$$
$$\begin{align*}p^{G}_{H}(v \otimes g_{i}) = \begin{cases} v& \text{if } i=1, \\ 0& \text{otherwise}, \end{cases} \end{align*}$$
 $v \in {\mathbb {F}}[t^{\pm 1}]^{d}$
is arbitrary.
$v \in {\mathbb {F}}[t^{\pm 1}]^{d}$
is arbitrary.
Using the claim, we take our first step in expanding
 $\langle x, (p^{G}_{H} \circ \overline {\phi })(y) \rangle _{d}$
. Indeed, observe that for any
$\langle x, (p^{G}_{H} \circ \overline {\phi })(y) \rangle _{d}$
. Indeed, observe that for any
 $x \in (\mathbb {F}(t) / {\mathbb {F}}[t^{\pm 1}])^{d}_{\beta } $
and any
$x \in (\mathbb {F}(t) / {\mathbb {F}}[t^{\pm 1}])^{d}_{\beta } $
and any
 $y = \sum _{i=1}^{n} y_{i} \otimes g_{i} \in {\mathbb {F}}[t^{\pm 1}]^{nd}_{\alpha }$
, the above formula implies that (A.17)We can expand
$y = \sum _{i=1}^{n} y_{i} \otimes g_{i} \in {\mathbb {F}}[t^{\pm 1}]^{nd}_{\alpha }$
, the above formula implies that (A.17)We can expand $$ \begin{align} \langle x, (p^{G}_{H} \circ \overline{\phi})(y) \rangle_{d} = \langle x, y_{1} \rangle_{d}. \end{align} $$
$$ \begin{align} \langle x, (p^{G}_{H} \circ \overline{\phi})(y) \rangle_{d} = \langle x, y_{1} \rangle_{d}. \end{align} $$
 $\langle i^{G}_{H}(x),y \rangle _{nd}$
using Lemma A.10: Consequently, the formula (A.16) is satisfied.
$\langle i^{G}_{H}(x),y \rangle _{nd}$
using Lemma A.10: Consequently, the formula (A.16) is satisfied. $$\begin{align*}\langle i^{G}_{H}(x),y \rangle_{nd} = \langle x \otimes g_{1}, y \rangle_{nd} = \sum_{i=1}^{n} \langle x \otimes g_{1}, y_{i} \otimes g_{i}\rangle_{nd} = \langle x \otimes g_{1}, y_{1} \otimes g_{1} \rangle_{nd} = \langle x,y_{1} \rangle_{d}.\end{align*}$$
$$\begin{align*}\langle i^{G}_{H}(x),y \rangle_{nd} = \langle x \otimes g_{1}, y \rangle_{nd} = \sum_{i=1}^{n} \langle x \otimes g_{1}, y_{i} \otimes g_{i}\rangle_{nd} = \langle x \otimes g_{1}, y_{1} \otimes g_{1} \rangle_{nd} = \langle x,y_{1} \rangle_{d}.\end{align*}$$
This was the required equality and as we mentioned above, we can now apply Lemma A.4 (with
 $\beta =\operatorname {id}$
,
$\beta =\operatorname {id}$
,
 $\alpha =p_H^G \circ \overline {\phi }$
and
$\alpha =p_H^G \circ \overline {\phi }$
and
 $\alpha '=i^G_H$
) to conclude that the bottom square in the diagram in (A.12) is commutative.
$\alpha '=i^G_H$
) to conclude that the bottom square in the diagram in (A.12) is commutative.
We have therefore proved that the three squares in (A.12) are commutative, and as we explained at the beginning of the proof, this implies that
![]() $\operatorname {\mathrm {Bl}}_{\beta }(M_{n}) \cong \operatorname {\mathrm {Bl}}_{\alpha }(M)$
, thus establishing the proposition.
$\operatorname {\mathrm {Bl}}_{\beta }(M_{n}) \cong \operatorname {\mathrm {Bl}}_{\alpha }(M)$
, thus establishing the proposition.
Acknowledgements
This paper together with [Reference Borodzik, Conway and Politarczyk3, Reference Borodzik, Conway and Politarczyk2] was originally part of a single paper titled ‘Twisted Blanchfield pairings and Casson–Gordon invariants’. During that project, the second named author was at University of Geneva and later at Durham University, supported by the Swiss National Science Foundation; during a subset of the revision and splitting process, he was a postdoc at the Max Planck Institute for Mathematics. The first named author is supported by the National Science Center grant 2019/B/35/ST1/01120. The third named author is supported by the National Science Center grant 2016/20/S/ST1/00369. All three authors wish to thank the University of Geneva and the University of Warsaw at which part of this work was conducted.
Competing interest
None.