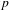Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lau, Eike
2021.
Higher frames and G-displays.
Algebra & Number Theory,
Vol. 15,
Issue. 9,
p.
2315.
Bartling, Sebastian
and
Hoff, Manuel
2025.
Moduli Spaces of Nilpotent Displays.
International Mathematics Research Notices,
Vol. 2025,
Issue. 3,