Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-06T09:58:56.876Z Has data issue: false hasContentIssue false
  • English
  • Français

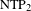STABILIZERS, $\text{NTP}_{2}$ GROUPS WITH $\text{f}$-GENERICS, AND PRC FIELDS

Part of: Model theory

Published online by Cambridge University Press:  10 May 2018

Samaria Montenegro ,
Alf Onshuus  and
Pierre Simon
Samaria Montenegro
Affiliation:
Escuela de Matemática-CIMPA, Universidad de Costa Rica, San José, Costa Rica ([email protected]) Departamento de Matemáticas, Universidad de los Andes, Bogotá, Colombia ([email protected])
Alf Onshuus
Affiliation:
Departamento de Matemáticas, Universidad de los Andes, Bogotá, Colombia ([email protected])
Pierre Simon
Affiliation:
Department of Mathematics, University of California, Berkeley, CA, USA ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

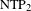In this paper, we develop three different subjects. We study and prove alternative versions of Hrushovski’s ‘stabilizer theorem’, we generalize part of the basic theory of definably amenable NIP groups to $\text{NTP}_{2}$ theories, and finally, we use all this machinery to study groups with f-generic types definable in bounded pseudo real closed fields.

Keywords

model theoryPRCf-genericsdefinable groupsNIPNTP2

MSC classification

Primary: 03C45: Classification theory, stability and related concepts 03C60: Model-theoretic algebra
Secondary: 03C98: Applications of model theory
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 3 , May 2020 , pp. 821 - 853
Copyright
© Cambridge University Press 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first and second authors were partially supported by Colciencias grant number 120471250707. The third author was partially supported by ValCoMo (ANR-13-BS01-0006), NSF (grant DMS 1665491), and the Sloan foundation.

References

Barriga, E., Definably compact groups definable in real closed fields. I, ArXiv e-prints, arXiv:1703.08606, March 2017.Google Scholar
Basarav, S. A., The absolute galois group of a pseudo real closed field with finitely many orders, J. Pure Appl. Algebra 38 (1985), 1–18.Google Scholar
Baisalov, Y. and Poizat, B., Paires de structures o-minimales, J. Symbolic Logic 63(2) (1998), 570–578.Google Scholar
Ben Yaacov, I. and Chernikov, A., An independence theorem for NTP2 theories, J. Symbolic Logic 79(1) (2014), 135–153.Google Scholar
Chernikov, A. and Kaplan, I., Forking and dividing in NTP2 theories, J. Symbolic Logic 77(1) (2012), 1–20.Google Scholar
Chernikov, A. and Simon, P., Externally definable sets and dependent pairs, Israel J. Math. 194(1) (2013), 409–425.Google Scholar
Chernikov, A. and Simon, P., Definably amenable NIP groups, J. Amer. Math. Soc. 31(3) (2018), 609–641.Google Scholar
Hrushovski, E. and Pillay, A., Groups definable in local fields and pseudo-finite fields, Israel J. Math. 85(1–3) (1994), 203–262.Google Scholar
Hrushovski, E. and Pillay, A., On NIP and invariant measures, J. Eur. Math. Soc. (JEMS) 13 (2011), 1005–1061.Google Scholar
Hrushovski, E., Peterzil, Y. and Pillay, A., Groups, measures, and the NIP, J. Amer. Math. Soc. 21(2) (2008), 563–596.Google Scholar
Hrushovski, E., Stable group theory and approximate subgroups, J. Amer. Math. Soc. 25(1) (2012), 189–243.Google Scholar
Jarden, M., The algebraic nature of the elementary theory of prc fields, Manuscripta Math. 60 (1988), 463–475.Google Scholar
Johnson, W., Forking and dividing in fields with several orderings and valuations, Preprint, 2013.Google Scholar
Macpherson, D., Marker, D. and Steinhorn, C., Weakly o-minimal structures and real closed fields, Trans. Amer. Math. Soc. 352(12) (2000), 5435–5483 (electronic).Google Scholar
Montenegro, S., Pseudo real closed fields, pseudo p-adically closed fields and ntp 2, Ann. Pure Appl. Logic 168(1) (2017), 191–232.Google Scholar
Prestel, A., Pseudo real closed fields, in Set Theory and Model Theory (Bonn, 1979), Lecture Notes in Math., Volume 872, pp. 127–156 (Springer, Berlin-New York, 1981).Google Scholar
Prestel, A. and Ziegler, M., Model-theoretic methods in the theory of topological fields, J. Reine Angew. Math. 299(300) (1978), 318–341.Google Scholar
Shelah, S., Dependent first order theories, continued, Israel J. Math. 173 (2009), 1–60.Google Scholar
Simon, P., A Guide to NIP Theories, Lecture Notes in Logic, Volume 44, p. vii+156 (Association for Symbolic Logic, Chicago, IL, 2015).Google Scholar
van den Dries, L., Tame Topology and O-minimal Structures, London Mathematical Society Lecture Note Series, Volume 248, p. x+180 (Cambridge University Press, Cambridge, 1998).Google Scholar