Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-24T01:30:33.696Z Has data issue: false hasContentIssue false
  • English
  • Français

RELATIVE UNITARY RZ-SPACES AND THE ARITHMETIC FUNDAMENTAL LEMMA

Part of: Arithmetic algebraic geometry Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  24 March 2020

Andreas Mihatsch Open the ORCID record for Andreas Mihatsch [Opens in a new window]
Andreas Mihatsch*
Affiliation:
Rheinische Friedrich-Wilhelms-Universitat Bonn, Mathematisches Institut, Endenicher Allee 60, Bonn, 53115, Germany ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove a comparison isomorphism between certain moduli spaces of 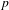$p$-divisible groups and strict 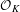${\mathcal{O}}_{K}$-modules (RZ-spaces). Both moduli problems are of PEL-type (polarization, endomorphism, level structure) and the difficulty lies in relating polarized 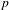$p$-divisible groups and polarized strict 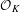${\mathcal{O}}_{K}$-modules. We use the theory of relative displays and frames, as developed by Ahsendorf, Lau and Zink, to translate this into a problem in linear algebra. As an application of these results, we verify new cases of the arithmetic fundamental lemma (AFL) of Wei Zhang: The comparison isomorphism yields an explicit description of certain cycles that play a role in the AFL. This allows, under certain conditions, to reduce the AFL identity in question to an AFL identity in lower dimension.

Keywords

moduli spacep-divisible groupdisplayarithmetic fundamental lemma

MSC classification

Primary: 11G18: Arithmetic aspects of modular and Shimura varieties
Secondary: 14G35: Modular and Shimura varieties
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 1 , January 2022 , pp. 241 - 301
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahsendorf, T., ${\mathcal{O}}$ -displays and $\unicode[STIX]{x1D70B}$ -divisible formal ${\mathcal{O}}$ -modules, PhD thesis, Universität Bielefeld (2011).Google Scholar
Ahsendorf, T., Cheng, Ch. and Zink, T., 𝓞-displays and 𝜋-divisible formal 𝓞-modules, J. Algebra 457 (2016), 129–193.CrossRefGoogle Scholar
Beuzart-Plessis, R., A new proof of Jacquet-Rallis’s fundamental lemma, Preprint, 2019, arXiv:1901.02653.Google Scholar
Cho, S., The basic locus of the unitary Shimura variety with parahoric level structure, and special cycles, Preprint, 2018, arXiv:1807.09997.Google Scholar
Fargues, L. and Fontaine, J.-M., Courbes et fibré vectoriel en théorie de Hodge p-adique, Astérisque 406 (2018), 1–382.CrossRefGoogle Scholar
Gan, W.-T., Gross, B. and Prasad, D., Symplectic root numbers, central critical values, and restriction problems in the representation theory of classical groups, Astérisque 346 (2012), 1–109.Google Scholar
Gordon, J., Transfer to characteristic zero, Appendix to [ 22 ].Google Scholar
He, X., Li, C. and Zhu, Y., Fine Deligne–Lusztig varieties and arithmetic fundamental lemmas, Forum of Mathematics, Sigma 7 (2019), E47.CrossRefGoogle Scholar
Kudla, S. and Rapoport, M., Special cycles on unitary Shimura varieties, I. Unramified local theory, Invent. Math. 184 (2011), 629–682.CrossRefGoogle Scholar
Lau, E., Displays and formal p-divisible groups, Invent. Math. 171 (2008), 617–628.CrossRefGoogle Scholar
Lau, E., Frames and finite group schemes over complete regular local rings, Doc. Math. 15 (2010), 545–569.Google Scholar
Li, C. and Zhu, Y., Remarks on the arithmetic fundamental lemma, Algebra Number Theory 11 (2017), 2425–2445.CrossRefGoogle Scholar
Li, C. and Zhu, Y., Arithmetic intersection on GSpin Rapoport–Zink spaces, Compos. Math. 154 (2018), 1407–1440.CrossRefGoogle Scholar
Mihatsch, A., On the arithmetic fundamental lemma through Lie algebras, Math. Z. 287 (2017), 181–197.CrossRefGoogle Scholar
Rapoport, M., Smithling, B. and Zhang, W., On the arithmetic transfer conjecture for exotic smooth formal moduli spaces, Duke Math. J. 166 (2017), 2183–2336.CrossRefGoogle Scholar
Rapoport, M., Smithling, B. and Zhang, W., Regular formal moduli spaces and arithmetic transfer conjectures, Math. Ann. 370 (2018), 1079–1175.CrossRefGoogle Scholar
Rapoport, M., Smithling, B. and Zhang, W., Arithmetic diagonal cycles on unitary Shimura varieties, Preprint, 2017, arXiv:1710.06962.Google Scholar
Rapoport, M., Terstiege, U. and Zhang, W., On the arithmetic fundamental lemma in the minuscule case, Compos. Math. 149 (2013), 1631–1666.CrossRefGoogle Scholar
Rapoport, M. and Zink, T., Period Spaces for p-divisible Groups, Annals of Mathematics Studies, Volume 141 (Princeton University Press, Princeton, 1996).CrossRefGoogle Scholar
Rapoport, M. and Zink, T., On the Drinfeld moduli problem of p-divisible groups, Camb. J. Math. 5 (2017), 229–279.CrossRefGoogle Scholar
Vollaard, I. and Wedhorn, T., The supersingular locus of the Shimura variety for GU (1, n - 1), II, Invent. Math. 184 (2011), 591–627.CrossRefGoogle Scholar
Zhiwei, Y., The fundamental lemma of Jacquet and Rallis, Duke Math. J. 156 (2011), 167–228.Google Scholar
Zhang, W., On arithmetic fundamental lemmas, Invent. Math. 188 (2012), 197–252.CrossRefGoogle Scholar
Zhang, W., Periods, cycles, and L-functions: a relative trace formula approach, in Proceedings of the International Congress of Mathematicians, pp. 487–521 (World Scientific, 2018).Google Scholar
Zink, T., The display of a formal p-divisible group, Astérisque 278 (2002), 127–248.Google Scholar