Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T01:25:10.004Z Has data issue: false hasContentIssue false
  • English
  • Français

REDUCTIONS OF POINTS ON ALGEBRAIC GROUPS

Part of: Discontinuous groups and automorphic forms Algebraic groups Arithmetic algebraic geometry

Published online by Cambridge University Press:  14 November 2019

Davide Lombardo Open the ORCID record for Davide Lombardo [Opens in a new window]  and
Antonella Perucca
Davide Lombardo
Affiliation:
University of Pisa, Largo Bruno Pontecorvo 5, 56127Pisa, Italy ([email protected])
Antonella Perucca
Affiliation:
University of Luxembourg. 6, avenue de la Fonte, 4364Esch-sur-Alzette, Luxembourg ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $A$ be the product of an abelian variety and a torus defined over a number field 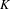$K$. Fix some prime number 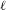$\ell$. If 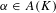$\unicode[STIX]{x1D6FC}\in A(K)$ is a point of infinite order, we consider the set of primes $\mathfrak{p}$ of 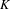$K$ such that the reduction 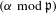$(\unicode[STIX]{x1D6FC}\hspace{0.2em}{\rm mod}\hspace{0.2em}\mathfrak{p})$ is well-defined and has order coprime to 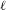$\ell$. This set admits a natural density. By refining the method of Jones and Rouse [Galois theory of iterated endomorphisms, Proc. Lond. Math. Soc. (3)100(3) (2010), 763–794. Appendix A by Jeffrey D. Achter], we can express the density as an 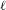$\ell$-adic integral without requiring any assumption. We also prove that the density is always a rational number whose denominator (up to powers of 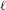$\ell$) is uniformly bounded in a very strong sense. For elliptic curves, we describe a strategy for computing the density which covers every possible case.

Keywords

reductionKummer theoryalgebraic groupsemiabelian varietyelliptic curveGalois representations

MSC classification

Primary: 11F80: Galois representations
Secondary: 14L10: Group varieties 11G05: Elliptic curves over global fields 11G10: Abelian varieties of dimension $> 1$
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 5 , September 2021 , pp. 1637 - 1669
Check for updates
Copyright
© Cambridge University Press 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Achter, J. D., Detecting complex multiplication, in Computational aspects of algebraic curves, Lecture Notes Ser. Comput., Volume 13, pp. 38–50 (World Sci. Publ., Hackensack, NJ, 2005).Google Scholar
Beilinson, A., p-adic periods and derived de Rham cohomology, J. Amer. Math. Soc. 25(3) (2012), 715–738.Google Scholar
Bogomolov, F. A., Points of finite order on abelian varieties, Izv. Akad. Nauk SSSR Ser. Mat. 44(4) (1980), 782–804. 973.Google Scholar
Bogomolov, F. A., Sur l’algébricité des représentations l-adiques, C. R. Acad. Sci. Paris Sér. A-B 290(15) (1980), A701–A703.Google Scholar
Breuillard, E., Green, B. and Tao, T., Approximate subgroups of linear groups, Geom. Funct. Anal. 21(4) (2011), 774–819.Google Scholar
Debry, C. and Perucca, A., Reductions of algebraic integers, J. Number Theory 167 (2016), 259–283.Google Scholar
Deligne, P., Théorie de Hodge. III, Publ. Math. Inst. Hautes Études Sci. 44 (1974), 5–77.Google Scholar
Denef, J., On the evaluation of certain p-adic integrals, in Séminaire de théorie des nombres, Paris 1983–84, Progr. Math., Volume 59, pp. 25–47 (Birkhäuser Boston, Boston, MA, 1985).Google Scholar
Faltings, G., p-adic Hodge theory, J. Amer. Math. Soc. 1(1) (1988), 255–299.Google Scholar
Fried, M. D. and Jarden, M., Field Arithmetic, 3rd edition, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge / A Series of Modern Surveys in Mathematics 11 (Springer, Berlin, Heidelberg, 2008).Google Scholar
Hasse, H., Uber die Dichte der Primzahlen p, für die eine vorgegebene ganzrationale Zahl a≠0 von durch eine vorgegebene Primzahl l≠2 teilbarer bzw. unteilbarer Ordnung mod p ist, Math. Ann. 162 (1965/1966), 74–76.Google Scholar
Hasse, H., Über die Dichte der Primzahlen p, für die eine vorgegebene ganzrationale Zahl a ≠ 0 von gerader bzw. ungerader Ordnung mod. p ist, Math. Ann. 166 (1966), 19–23.Google Scholar
Jones, R. and Rouse, J., Galois theory of iterated endomorphisms, Proc. Lond. Math. Soc. (3) 100(3) (2010), 763–794. Appendix A by Jeffrey D. Achter.Google Scholar
Kowalski, E., Some local–global applications of Kummer theory, Manuscripta Math. 111(1) (2003), 105–139.Google Scholar
Larsen, M. and Pink, R., A connectedness criterion for l-adic Galois representations, Israel J. Math. 97 (1997), 1–10.Google Scholar
Lombardo, D. and Perucca, A., The 1-eigenspace for matrices in GL2(ℤℓ), New York J. Math. 23 (2017), 897–925.Google Scholar
Macintyre, A., Rationality of p-adic Poincaré series: uniformity in p, Ann. Pure Appl. Logic 49(1) (1990), 31–74.Google Scholar
Mattuck, A., Abelian varieties over p-adic ground fields, Ann. of Math. (2) 62 (1955), 92–119.Google Scholar
Moree, P., Artin’s primitive root conjecture—a survey, Integers 12(6) (2012), 1305–1416.Google Scholar
Oesterlé, J., Réduction modulo p n des sous-ensembles analytiques fermés de Z p N , Invent. Math. 66(2) (1982), 325–341.Google Scholar
Perucca, A., Prescribing valuations of the order of a point in the reductions of abelian varieties and tori, J. Number Theory 129(2) (2009), 469–476.Google Scholar
Perucca, A., The order of the reductions of an algebraic integer, J. Number Theory 148 (2015), 121–136.Google Scholar
Perucca, A., Reductions of 1-dimensional tori, Int. J. Number Theory 13(6) (2017), 1473–1489.Google Scholar
Pink, R., l-adic algebraic monodromy groups, cocharacters, and the Mumford–Tate conjecture, J. Reine Angew. Math. 495 (1998), 187–237.Google Scholar
Pink, R., On the order of the reduction of a point on an abelian variety, Math. Ann. 330(2) (2004), 275–291.Google Scholar
Richardson, R. W. Jr, A rigidity theorem for subalgebras of Lie and associative algebras, Illinois J. Math. 11 (1967), 92–110.Google Scholar
Rouse, J. and Zureick-Brown, D., Elliptic curves over ℚ and 2-adic images of galois, Res. Number Theory 1 (2015), Art. 12, 34pp.Google Scholar
Serre, J.-P., Propriétés galoisiennes des points d’ordre fini des courbes elliptiques, Invent. Math. 15(4) (1972), 259–331.Google Scholar
Serre, J.-P., Quelques applications du théorème de densité de Chebotarev, Publ. Math. Inst. Hautes Études Sci. (54) (1981), 323–401.Google Scholar
Serre, J.-P., Résumé des cours de 1984–1985, Annuaire du Collg̀e de France, 1985.Google Scholar
Serre, J.-P. and Tate, J., Good reduction of abelian varieties, Ann. of Math. (2) 88 (1968), 492–517.Google Scholar
Szamuely, T. and Zábrádi, G., The p-adic Hodge decomposition according to Beilinson, in Algebraic Geometry: Salt Lake City 2015 (ed. de Fernex, T. et al. ), Proceedings of Symposia in Pure Mathematics, vol. 97, Part 2, pp. 495–572 (American Mathematical Society, Providence, 2018).Google Scholar
The LMFDB Collaboration, The L-functions and modular forms database. http://www.lmfdb.org, 2016.Google Scholar
The Sage Developers, SageMath, the Sage Mathematics Software System (Version 7.5.1), 2017. http://www.sagemath.org.Google Scholar
The Stacks Project Authors, Stacks Project. http://stacks.math.columbia.edu, 2017.Google Scholar
Wintenberger, J.-P., Démonstration d’une conjecture de Lang dans des cas particuliers, J. Reine Angew. Math. 553 (2002), 1–16.Google Scholar