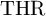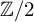1 Introduction
Hochschild and cyclic homology and their refinements
![]() ${\mathrm {THH}}$
and
${\mathrm {THH}}$
and
![]() $\mathrm {TC}$
have been extensively studied for many decades, both for their own sake and for their deep connections with algebraic K-theory via traces; see, for example, [Reference Bökstedt, Hsiang and Madsen11]. Standard textbook references include [Reference Loday and Ronco40] and [Reference Dundas, Goodwillie and McCarthy19]. More recently, Bhatt–Morrow–Scholze [Reference Bhatt, Morrow and Scholze7] have introduced a filtration on
$\mathrm {TC}$
have been extensively studied for many decades, both for their own sake and for their deep connections with algebraic K-theory via traces; see, for example, [Reference Bökstedt, Hsiang and Madsen11]. Standard textbook references include [Reference Loday and Ronco40] and [Reference Dundas, Goodwillie and McCarthy19]. More recently, Bhatt–Morrow–Scholze [Reference Bhatt, Morrow and Scholze7] have introduced a filtration on
![]() ${\mathrm {THH}}$
and
${\mathrm {THH}}$
and
![]() $\mathrm {TC}$
that is strongly related to integral p-adic Hodge theory. Hahn–Raksit–Wilson [Reference Hahn, Raksit and Wilson25] have provided an alternative construction of the filtration that applies to commutative ring spectra satisfying certain assumptions.
$\mathrm {TC}$
that is strongly related to integral p-adic Hodge theory. Hahn–Raksit–Wilson [Reference Hahn, Raksit and Wilson25] have provided an alternative construction of the filtration that applies to commutative ring spectra satisfying certain assumptions.
Both topological and algebraic K-theory have real or Hermitian refinements. This is also true for
![]() ${\mathrm {THH}}$
and
${\mathrm {THH}}$
and
![]() $\mathrm {TC}$
, but the serious study of their real variants
$\mathrm {TC}$
, but the serious study of their real variants
![]() $\mathrm {THR}$
and
$\mathrm {THR}$
and
![]() $\mathrm {TCR}$
has just started; see, for example, [Reference Dotto and Ogle17], [Reference Dotto, Moi, Patchkoria and Reeh16] and [Reference Quigley and Shah48]. These theories apply to very different branches in algebra and geometry: commutative rings, group rings, schemes, ring spectra, …all with or without a nontrivial involution. Concerning the
$\mathrm {TCR}$
has just started; see, for example, [Reference Dotto and Ogle17], [Reference Dotto, Moi, Patchkoria and Reeh16] and [Reference Quigley and Shah48]. These theories apply to very different branches in algebra and geometry: commutative rings, group rings, schemes, ring spectra, …all with or without a nontrivial involution. Concerning the
![]() ${\mathbb {Z}/2}$
-equivariant cyclotomic trace, we understand that there is work in progress by Harpaz, Nikolaus and Shah studying this map in the very general setting of stable Poincaré
${\mathbb {Z}/2}$
-equivariant cyclotomic trace, we understand that there is work in progress by Harpaz, Nikolaus and Shah studying this map in the very general setting of stable Poincaré
![]() $\infty $
-categories. (When studying traces, beware of the difference between rings, which is what most algebraic K-theorists and algebraic geometers look at, and ring spectra, which are the input of
$\infty $
-categories. (When studying traces, beware of the difference between rings, which is what most algebraic K-theorists and algebraic geometers look at, and ring spectra, which are the input of
![]() ${\mathrm {THH}}$
and
${\mathrm {THH}}$
and
![]() $\mathrm {TC}$
.)
$\mathrm {TC}$
.)
The current article contributes to a better understanding of
![]() $\mathrm {THR}$
in algebraic geometry, although some of our results also apply to other settings. Our first main result is the base change result in Theorem 3.2.3 for the isovariant étale topology. This then is one of the main ingredients in the proof of the following isovariant étale descent theorem for
$\mathrm {THR}$
in algebraic geometry, although some of our results also apply to other settings. Our first main result is the base change result in Theorem 3.2.3 for the isovariant étale topology. This then is one of the main ingredients in the proof of the following isovariant étale descent theorem for
![]() $\mathrm {THR}$
.
$\mathrm {THR}$
.
Theorem 3.4.3. The presheaf
satisfies isovariant étale descent, where
![]() $\mathbf {Aff}_{{\mathbb {Z}/2}}$
denotes the category of affine schemes with involutions, and
$\mathbf {Aff}_{{\mathbb {Z}/2}}$
denotes the category of affine schemes with involutions, and
![]() $\mathrm {Sp}_{{\mathbb {Z}/2}}$
denotes the
$\mathrm {Sp}_{{\mathbb {Z}/2}}$
denotes the
![]() $\infty $
-category of
$\infty $
-category of
![]() ${\mathbb {Z}/2}$
-spectra.
${\mathbb {Z}/2}$
-spectra.
In the nonequivariant case, similar results have been established for
![]() ${\mathrm {THH}}$
and
${\mathrm {THH}}$
and
![]() $\mathrm {TC}$
by Weibel–Geller [Reference Weibel and Geller60] and Geisser–Hesselholt [Reference Geisser and Hesselholt21].
$\mathrm {TC}$
by Weibel–Geller [Reference Weibel and Geller60] and Geisser–Hesselholt [Reference Geisser and Hesselholt21].
This descent theorem implies in particular that
![]() $\mathrm {THR}$
satisfies the equivariant Zariski–Mayer–Vietoris property for affine schemes with involutions. This can be used to extend
$\mathrm {THR}$
satisfies the equivariant Zariski–Mayer–Vietoris property for affine schemes with involutions. This can be used to extend
![]() $\mathrm {THR}$
to nonaffine schemes with involutions; see Definition 3.4.6, in a way that is compatible with existing definitions of
$\mathrm {THR}$
to nonaffine schemes with involutions; see Definition 3.4.6, in a way that is compatible with existing definitions of
![]() ${\mathrm {THH}}$
, see Proposition 3.4.7.
${\mathrm {THH}}$
, see Proposition 3.4.7.
Using this Zariski–Mayer–Vietoris theorem and various explicit computations of
![]() $\mathrm {THR}$
of products of monoid rings and maps between them, we are able to compute
$\mathrm {THR}$
of products of monoid rings and maps between them, we are able to compute
![]() $\mathrm {THR}(X)$
for
$\mathrm {THR}(X)$
for
![]() $X=\mathbb {P}^1,\mathbb {P}^{\sigma }$
and more generally
$X=\mathbb {P}^1,\mathbb {P}^{\sigma }$
and more generally
![]() $\mathbb {P}^n$
with trivial involution; see Theorems 5.1.2, 5.1.4 and 5.2.6. Here.
$\mathbb {P}^n$
with trivial involution; see Theorems 5.1.2, 5.1.4 and 5.2.6. Here.
![]() $\mathbb {P}^{\sigma }$
denotes the projective line with the involution switching the homogeneous coordinates. We recall that Blumberg and Mandell [Reference Blumberg and Mandell10] compute
$\mathbb {P}^{\sigma }$
denotes the projective line with the involution switching the homogeneous coordinates. We recall that Blumberg and Mandell [Reference Blumberg and Mandell10] compute
![]() ${\mathrm {THH}}(\mathbb {P}^n)$
. For
${\mathrm {THH}}(\mathbb {P}^n)$
. For
![]() $\mathbb {P}^n$
with the trivial involution, we obtain the following.
$\mathbb {P}^n$
with the trivial involution, we obtain the following.
Theorem 5.2.6. For any separated scheme with involution X and integer
![]() $n\geq 0$
, there is an equivalence of
$n\geq 0$
, there is an equivalence of
![]() ${\mathbb {Z}/2}$
-spectra
${\mathbb {Z}/2}$
-spectra
 $$\begin{align*}\mathrm{THR}(X\times \mathbb{P}^{n}) \simeq \left\{ \begin{array}{ll} \mathrm{THR}(X) \oplus \bigoplus_{j=1}^{\lfloor n/2 \rfloor} i_*{\mathrm{THH}}(X) & \text{if } n \text{ is even,}\\ \mathrm{THR}(X) \oplus \bigoplus_{j=1}^{\lfloor n/2 \rfloor} i_*{\mathrm{THH}}(X) \oplus \Sigma^{n(\sigma-1)}\mathrm{THR}(X) & \text{if } n \text{ is odd.} \end{array} \right. \end{align*}$$
$$\begin{align*}\mathrm{THR}(X\times \mathbb{P}^{n}) \simeq \left\{ \begin{array}{ll} \mathrm{THR}(X) \oplus \bigoplus_{j=1}^{\lfloor n/2 \rfloor} i_*{\mathrm{THH}}(X) & \text{if } n \text{ is even,}\\ \mathrm{THR}(X) \oplus \bigoplus_{j=1}^{\lfloor n/2 \rfloor} i_*{\mathrm{THH}}(X) \oplus \Sigma^{n(\sigma-1)}\mathrm{THR}(X) & \text{if } n \text{ is odd.} \end{array} \right. \end{align*}$$
For a
![]() ${\mathbb {Z}/2}$
-spectra E,
${\mathbb {Z}/2}$
-spectra E,
![]() $i_*E:=E \oplus E$
with the obvious involution, see equation (A.15). We refer to Remarks 2.0.1, 5.1.1 and 5.2.7 for a comparison with Hermitian and real algebraic K-theory.
$i_*E:=E \oplus E$
with the obvious involution, see equation (A.15). We refer to Remarks 2.0.1, 5.1.1 and 5.2.7 for a comparison with Hermitian and real algebraic K-theory.
Recall that, unlike algebraic and Hermitian K-theory,
![]() ${\mathrm {THH}}$
and
${\mathrm {THH}}$
and
![]() $\mathrm {THR}$
are not
$\mathrm {THR}$
are not
![]() $\mathbb {A}^1$
-invariant even on regular schemes. On the other hand,
$\mathbb {A}^1$
-invariant even on regular schemes. On the other hand,
![]() ${\mathrm {THH}}$
and
${\mathrm {THH}}$
and
![]() $\mathrm {TC}$
do extend to log schemes, and using descent, trivial
$\mathrm {TC}$
do extend to log schemes, and using descent, trivial
![]() $\mathbb {P}^1$
-bundle formula and computations on the log schemes
$\mathbb {P}^1$
-bundle formula and computations on the log schemes
![]() $(\mathbb {P}^n,\mathbb {P}^{n-1})$
, can be shown to be representable in the log-variant of the
$(\mathbb {P}^n,\mathbb {P}^{n-1})$
, can be shown to be representable in the log-variant of the
![]() $\mathbb {P}^1$
-stable motivic Morel–Voevodsky homotopy category. This is done in the very recent joint work [Reference Binda, Park and Østvær8] of the second author with Federico Binda and Paul Arne Østvær. We refer to [Reference Binda, Park and Østvær9] for an overview of their work. The results of this article are expected to provide most of the necessary ingredients for showing stable representability of
$\mathbb {P}^1$
-stable motivic Morel–Voevodsky homotopy category. This is done in the very recent joint work [Reference Binda, Park and Østvær8] of the second author with Federico Binda and Paul Arne Østvær. We refer to [Reference Binda, Park and Østvær9] for an overview of their work. The results of this article are expected to provide most of the necessary ingredients for showing stable representability of
![]() $\mathrm {THR}$
or at least its fixed points
$\mathrm {THR}$
or at least its fixed points
![]() $\mathrm {THO}$
in the corresponding equivariant log-homotopy categories. Furthermore, the work of Quigley–Shah [Reference Quigley and Shah48] allows us to extend many results of this article including Theorems 3.4.3 and 5.2.6 to
$\mathrm {THO}$
in the corresponding equivariant log-homotopy categories. Furthermore, the work of Quigley–Shah [Reference Quigley and Shah48] allows us to extend many results of this article including Theorems 3.4.3 and 5.2.6 to
![]() $\mathrm {TCR}$
. The second author hopes to carry out motivic representability of
$\mathrm {TCR}$
. The second author hopes to carry out motivic representability of
![]() $\mathrm {THR}$
and
$\mathrm {THR}$
and
![]() $\mathrm {TCR}$
in forthcoming work.
$\mathrm {TCR}$
in forthcoming work.
We conclude with a short overview of the different sections. Section 2 discusses some generalities about commutative ring spectra with involutions and their
![]() $\mathrm {THR}$
. This includes the study of several functors between
$\mathrm {THR}$
. This includes the study of several functors between
![]() ${\mathbb {Z}/2}$
-equivariant and nonequivariant categories, including the norm and equivariant notion of flatness. The necessary background on G-stable equivariant homotopy theory for finite groups G, both
${\mathbb {Z}/2}$
-equivariant and nonequivariant categories, including the norm and equivariant notion of flatness. The necessary background on G-stable equivariant homotopy theory for finite groups G, both
![]() ${\infty }$
- and model categorical, is provided in Appendix A. Section 3 reviews and extends several definitions for Grothendieck topologies on schemes with involutions, notably Thomason’s isovariant étale topology. Base change and descent for
${\infty }$
- and model categorical, is provided in Appendix A. Section 3 reviews and extends several definitions for Grothendieck topologies on schemes with involutions, notably Thomason’s isovariant étale topology. Base change and descent for
![]() $\mathrm {THR}$
are established in subsections 3.2 and 3.4. Note that the proof of étale base change in subsection 3.2 heavily relies on various results about Green functors established in subsections Appendix A.4 and Appendix A.5. Section 4 recollects and extends material on real and dihedral nerves, which is crucial when computing
$\mathrm {THR}$
are established in subsections 3.2 and 3.4. Note that the proof of étale base change in subsection 3.2 heavily relies on various results about Green functors established in subsections Appendix A.4 and Appendix A.5. Section 4 recollects and extends material on real and dihedral nerves, which is crucial when computing
![]() $\mathrm {THR}$
of spherical monoid rings and of monoid rings over Eilenberg MacLane spectra, and where the monoids may have involutions. These monoid ring computations together with isovariant Zariski descent are then used in the computations for projective spaces in section 5.
$\mathrm {THR}$
of spherical monoid rings and of monoid rings over Eilenberg MacLane spectra, and where the monoids may have involutions. These monoid ring computations together with isovariant Zariski descent are then used in the computations for projective spaces in section 5.
2 Real topological Hochschild homology of rings with involutions
Remark 2.0.1.
![]() $\mathrm {THR}$
is to real algebraic K-theory
$\mathrm {THR}$
is to real algebraic K-theory
![]() $\mathbf {KR}$
what
$\mathbf {KR}$
what
![]() ${\mathrm {THH}}$
is to algebraic K-theory. Hence, we recall some recent results on real algebraic K-theory
${\mathrm {THH}}$
is to algebraic K-theory. Hence, we recall some recent results on real algebraic K-theory
![]() $\mathbf {KR}$
. This is a
$\mathbf {KR}$
. This is a
![]() ${\mathbb {Z}/2}$
-equivariant motivic spectrum constructed in [Reference Hu, Kriz and Ormsby34] and [Reference Carmody12]. We recover Hermitian K-theory when restricting
${\mathbb {Z}/2}$
-equivariant motivic spectrum constructed in [Reference Hu, Kriz and Ormsby34] and [Reference Carmody12]. We recover Hermitian K-theory when restricting
![]() $\mathbf {KR}$
to schemes with trivial
$\mathbf {KR}$
to schemes with trivial
![]() ${\mathbb {Z}/2}$
-action. (This is one incarnation of the philosophy ‘the fixed points of
${\mathbb {Z}/2}$
-action. (This is one incarnation of the philosophy ‘the fixed points of
![]() $\mathbf {KR}$
are Hermitian K-theory’ in the world of presheaves on
$\mathbf {KR}$
are Hermitian K-theory’ in the world of presheaves on
![]() ${\mathbb {Z}/2}$
-schemes). Forgetting the action, we recover Voevodsky’s algebraic K-theory spectrum
${\mathbb {Z}/2}$
-schemes). Forgetting the action, we recover Voevodsky’s algebraic K-theory spectrum
![]() $KGL$
. As observed in [Reference Xie61, section 7.3], see also [Reference Carmody12], Schlichting’s techniques generalize to show that
$KGL$
. As observed in [Reference Xie61, section 7.3], see also [Reference Carmody12], Schlichting’s techniques generalize to show that
![]() $\mathbf {KR}$
is representable in
$\mathbf {KR}$
is representable in
![]() $\mathcal {SH}^{\mathbb {Z}/2}(k)$
. In particular,
$\mathcal {SH}^{\mathbb {Z}/2}(k)$
. In particular,
![]() $\mathbf {KR}$
satisfies equivariant Nisnevich descent. Here and below, following [Reference Carmody12] and [Reference Hu, Kriz and Ormsby34], we consider
$\mathbf {KR}$
satisfies equivariant Nisnevich descent. Here and below, following [Reference Carmody12] and [Reference Hu, Kriz and Ormsby34], we consider
![]() $\mathbf {KR}$
as a motivic spectrum with respect to the circle
$\mathbf {KR}$
as a motivic spectrum with respect to the circle
![]() $T^{\rho } \simeq \mathbb {P}^1 \wedge \mathbb {P}^{\sigma }$
, where
$T^{\rho } \simeq \mathbb {P}^1 \wedge \mathbb {P}^{\sigma }$
, where
![]() $\rho $
is the regular representation of
$\rho $
is the regular representation of
![]() ${\mathbb {Z}/2}$
, and
${\mathbb {Z}/2}$
, and
![]() $\mathbb {P}^{\sigma }$
denotes
$\mathbb {P}^{\sigma }$
denotes
![]() $\mathbb {P}^1$
with involution switching the homogeneous coordinates. It might be more consistent with the notations for
$\mathbb {P}^1$
with involution switching the homogeneous coordinates. It might be more consistent with the notations for
![]() ${\mathrm {THH}}$
to denote the (motivic) Hermitian K-theory spectrum on schemes with involution by
${\mathrm {THH}}$
to denote the (motivic) Hermitian K-theory spectrum on schemes with involution by
![]() $\mathbf {KO}$
and to reserve the notation
$\mathbf {KO}$
and to reserve the notation
![]() $\mathbf {KR}$
for a (motivic) spectrum with involution whose fixed points are
$\mathbf {KR}$
for a (motivic) spectrum with involution whose fixed points are
![]() $\mathbf {KO}$
. For further results on
$\mathbf {KO}$
. For further results on
![]() $\mathbf {KR}$
and projective spaces, we refer to Remarks 5.1.1 and 5.2.7 below.
$\mathbf {KR}$
and projective spaces, we refer to Remarks 5.1.1 and 5.2.7 below.
Throughout this section, we fix morphisms of finite groupoids
where
![]() $\mathrm {B} G$
denotes the finite groupoid consisting of a single set
$\mathrm {B} G$
denotes the finite groupoid consisting of a single set
![]() $*$
with
$*$
with
![]() $\operatorname {\mathrm {Hom}}_{\mathrm {B} G}(*,*):=G$
. According to section Appendix A.2, we often use the alternative notation
$\operatorname {\mathrm {Hom}}_{\mathrm {B} G}(*,*):=G$
. According to section Appendix A.2, we often use the alternative notation
instead of the notation in section Appendix A.1. In particular, all functors in the sequel are
![]() $\infty $
-functors, which admit lifts to Quillen functors between model categories.
$\infty $
-functors, which admit lifts to Quillen functors between model categories.
We then have adjoint pairs
and functors
By [Reference Schwede53, Theorem 7.12], the pair of functors
![]() $(i^*,\Phi ^{{\mathbb {Z}/2}})$
is conservative. We will use this fact frequently. We also have adjoint pairs
$(i^*,\Phi ^{{\mathbb {Z}/2}})$
is conservative. We will use this fact frequently. We also have adjoint pairs
 $$ \begin{gather*} N^{{\mathbb{Z}/2}}:\mathrm{CAlg} \rightleftarrows \mathrm{NAlg}_{{\mathbb{Z}/2}} : i^*, \text{ } i^*:\mathrm{NAlg}_{{\mathbb{Z}/2}}\rightleftarrows \mathrm{CAlg} : i_*, \\ \text{ and } \iota : \mathrm{CAlg} \rightleftarrows \mathrm{CAlg}_{{\mathbb{Z}/2}} : (-)^{{\mathbb{Z}/2}} \end{gather*} $$
$$ \begin{gather*} N^{{\mathbb{Z}/2}}:\mathrm{CAlg} \rightleftarrows \mathrm{NAlg}_{{\mathbb{Z}/2}} : i^*, \text{ } i^*:\mathrm{NAlg}_{{\mathbb{Z}/2}}\rightleftarrows \mathrm{CAlg} : i_*, \\ \text{ and } \iota : \mathrm{CAlg} \rightleftarrows \mathrm{CAlg}_{{\mathbb{Z}/2}} : (-)^{{\mathbb{Z}/2}} \end{gather*} $$
and a colimit preserving functor
We refer sections Appendix A.1 and Appendix A.2 for further properties of all these functors.
We now define real topological Hochschild homology for commutative ring spectra with involution.
2.1 Definition of THR
Definition 2.1.1. Suppose
![]() $A\in \mathrm {NAlg}_{{\mathbb {Z}/2}}$
. For abbreviation, we set
$A\in \mathrm {NAlg}_{{\mathbb {Z}/2}}$
. For abbreviation, we set
Since
![]() $N^{{\mathbb {Z}/2}}$
is left adjoint to
$N^{{\mathbb {Z}/2}}$
is left adjoint to
![]() $i^*$
, we have the counit map
$i^*$
, we have the counit map
![]() $A^{\wedge {\mathbb {Z}/2}}\to A$
. We use this map to define
$A^{\wedge {\mathbb {Z}/2}}\to A$
. We use this map to define
which is called the real topological Hochschild homology of A. The first
![]() $\wedge $
in the formulation of
$\wedge $
in the formulation of
![]() $\mathrm {THR}$
is the pushout in
$\mathrm {THR}$
is the pushout in
![]() $\mathrm {NAlg}_{{\mathbb {Z}/2}}$
. Under a certain flatness condition, this is equivalent to the Bökstedt model of the real topological Hochschild homology; see [Reference Dotto, Moi, Patchkoria and Reeh16, Theorem, p. 65]. Note also that it is possible to define
$\mathrm {NAlg}_{{\mathbb {Z}/2}}$
. Under a certain flatness condition, this is equivalent to the Bökstedt model of the real topological Hochschild homology; see [Reference Dotto, Moi, Patchkoria and Reeh16, Theorem, p. 65]. Note also that it is possible to define
![]() $\mathrm {THR}$
for
$\mathrm {THR}$
for
![]() ${\mathbb {Z}/2}$
-spectra with slightly less structure, for example, for
${\mathbb {Z}/2}$
-spectra with slightly less structure, for example, for
![]() $\mathbb {E}_{\sigma }$
-algebras as in [Reference Angelini-Knoll, Gerhardt and Hill1].
$\mathbb {E}_{\sigma }$
-algebras as in [Reference Angelini-Knoll, Gerhardt and Hill1].
The map to the second smash factor in
![]() $A\wedge _{A^{\wedge {\mathbb {Z}/2}}} A$
gives a canonical map
$A\wedge _{A^{\wedge {\mathbb {Z}/2}}} A$
gives a canonical map
In analogy with Hermitian K-theory
![]() $\mathbf {KO}$
and real algebraic K-theory
$\mathbf {KO}$
and real algebraic K-theory
![]() $\mathbf {KR}$
, we define
$\mathbf {KR}$
, we define
for
![]() $A \in \mathrm {NAlg}_{{\mathbb {Z}/2}}$
. For
$A \in \mathrm {NAlg}_{{\mathbb {Z}/2}}$
. For
![]() $B\in \mathrm {NAlg}=\mathrm {CAlg}$
, recall that the topological Hochschild homology of B is defined to be
$B\in \mathrm {NAlg}=\mathrm {CAlg}$
, recall that the topological Hochschild homology of B is defined to be
which in turn generalizes the classical [Reference Loday and Ronco40, Proposition 1.1.13] from rings to ring spectra.
Definition 2.1.2. Let
![]() $\mathcal {C}$
be a category. An object X of
$\mathcal {C}$
be a category. An object X of
![]() $\mathrm {Fun}(\mathrm {B} ({\mathbb {Z}/2}),\mathcal {C})$
is called an object of
$\mathrm {Fun}(\mathrm {B} ({\mathbb {Z}/2}),\mathcal {C})$
is called an object of
![]() $\mathcal {C}$
with involution. Explicitly, X is an object of
$\mathcal {C}$
with involution. Explicitly, X is an object of
![]() $\mathcal {C}$
equipped with an automorphism
$\mathcal {C}$
equipped with an automorphism
![]() $w\colon X\to X$
such that
$w\colon X\to X$
such that
![]() $w\circ w=\mathrm {id}$
.
$w\circ w=\mathrm {id}$
.
In particular, we have the notions of commutative rings with involutions, commutative monoids with involutions and so on.
We do not discuss definitions of
![]() $\mathrm {HR}(A)$
refining
$\mathrm {HR}(A)$
refining
![]() $\mathrm {HH}(A)$
and comparison results between
$\mathrm {HH}(A)$
and comparison results between
![]() $\mathrm {THR}(A)$
and
$\mathrm {THR}(A)$
and
![]() $\mathrm {HR}(A)$
, similarly to, for example, [Reference Nikolaus and Scholze46, Proposition IV.4.2], but see Remark 4.2.3 below. The adjoint functors
$\mathrm {HR}(A)$
, similarly to, for example, [Reference Nikolaus and Scholze46, Proposition IV.4.2], but see Remark 4.2.3 below. The adjoint functors
![]() $\underline {\pi }_0$
and
$\underline {\pi }_0$
and
![]() $\mathrm {H}$
, which are studied in the appendix, preserve many of the adjunctions we study; see, for example, Definition 2.3.2.
$\mathrm {H}$
, which are studied in the appendix, preserve many of the adjunctions we study; see, for example, Definition 2.3.2.
Proposition 2.1.3. For
![]() $A\in \mathrm {NAlg}_{{\mathbb {Z}/2}}$
and
$A\in \mathrm {NAlg}_{{\mathbb {Z}/2}}$
and
![]() $B\in \mathrm {CAlg}$
, there exist canonical equivalences
$B\in \mathrm {CAlg}$
, there exist canonical equivalences
Hence, there exists a canonical equivalence
In particular, the first equivalence implies
![]() $i^*\mathrm {THR}(\iota B) \simeq {\mathrm {THH}}(B)$
, using (2) of Proposition Appendix A.2.7.
$i^*\mathrm {THR}(\iota B) \simeq {\mathrm {THH}}(B)$
, using (2) of Proposition Appendix A.2.7.
Proof. Since
![]() $N^{{\mathbb {Z}/2}}$
and
$N^{{\mathbb {Z}/2}}$
and
![]() $i^*$
preserve colimits, we have equivalences
$i^*$
preserve colimits, we have equivalences
and
by Proposition Appendix A.2.7(6).
Proposition 2.1.4. For
![]() $B\in \mathrm {CAlg}$
, there exists a canonical equivalence
$B\in \mathrm {CAlg}$
, there exists a canonical equivalence
Proof. The composite
defines equation (2.4), where the first (resp. third) map is induced by the unit (resp. counit). Proposition 2.1.3 shows that the induced map
is an equivalence. By [Reference Schwede53, Theorem 7.12] (note that
![]() $i^*=\Phi ^e$
), it remains to show that the induced map
$i^*=\Phi ^e$
), it remains to show that the induced map
is an equivalence. The right-hand side is equivalent to
![]() $0$
by Proposition Appendix A.2.7(3),(5). On the other hand, we have equivalences
$0$
by Proposition Appendix A.2.7(3),(5). On the other hand, we have equivalences
which is equivalent to
![]() $0$
too.
$0$
too.
Applying
![]() $i^*$
and Proposition Appendix A.2.7(2), we obtain
$i^*$
and Proposition Appendix A.2.7(2), we obtain
![]() $\mathrm {THO}(i_*B) \simeq {\mathrm {THH}}(B)$
, which compares nicely with the well-known
$\mathrm {THO}(i_*B) \simeq {\mathrm {THH}}(B)$
, which compares nicely with the well-known
![]() $\mathbf {KO}(X\amalg X)\simeq K(X)$
for schemes X, where the involution on
$\mathbf {KO}(X\amalg X)\simeq K(X)$
for schemes X, where the involution on
![]() $X\amalg X$
switches the components.
$X\amalg X$
switches the components.
Proposition 2.1.5. Let
![]() $R\to A,B$
be maps in
$R\to A,B$
be maps in
![]() $\mathrm {NAlg}_{{\mathbb {Z}/2}}$
. Then there exists a canonical equivalence
$\mathrm {NAlg}_{{\mathbb {Z}/2}}$
. Then there exists a canonical equivalence
Proof. Both
![]() $N^{{\mathbb {Z}/2}}$
and
$N^{{\mathbb {Z}/2}}$
and
![]() $i^*$
preserve colimits. Hence, we obtain a canonical equivalence
$i^*$
preserve colimits. Hence, we obtain a canonical equivalence
On the other hand, there are canonical equivalences
 $$ \begin{align*} \mathrm{THR}(A)\wedge_{\mathrm{THR}(R)}\mathrm{THR}(B) &\simeq (A\wedge_{A^{\wedge {\mathbb{Z}/2}}} A) \wedge_{R\wedge_{R^{\wedge {\mathbb{Z}/2}}} R} (B\wedge_{B^{\wedge {\mathbb{Z}/2}}} B) \\ &\simeq (A\wedge_R B) \wedge_{A^{\wedge {\mathbb{Z}/2}}\wedge_{R^{\wedge {\mathbb{Z}/2}}}B^{\wedge {\mathbb{Z}/2}}} (A\wedge_R B). \end{align*} $$
$$ \begin{align*} \mathrm{THR}(A)\wedge_{\mathrm{THR}(R)}\mathrm{THR}(B) &\simeq (A\wedge_{A^{\wedge {\mathbb{Z}/2}}} A) \wedge_{R\wedge_{R^{\wedge {\mathbb{Z}/2}}} R} (B\wedge_{B^{\wedge {\mathbb{Z}/2}}} B) \\ &\simeq (A\wedge_R B) \wedge_{A^{\wedge {\mathbb{Z}/2}}\wedge_{R^{\wedge {\mathbb{Z}/2}}}B^{\wedge {\mathbb{Z}/2}}} (A\wedge_R B). \end{align*} $$
Combine the two equations to obtain the desired equivalence.
2.2 Mackey functors for
 ${\mathbb {Z}/2}$
${\mathbb {Z}/2}$
We refer to the appendix for a general discussion of Mackey and Green functors for finite groups G. We now restrict to the case
![]() $G={\mathbb {Z}/2}$
.
$G={\mathbb {Z}/2}$
.
Example 2.2.1. According to [Reference Schwede53, Example 4.38], a Mackey functor C for
![]() $G:={\mathbb {Z}/2}$
can be described as a diagram
$G:={\mathbb {Z}/2}$
can be described as a diagram

where
![]() $C(G/e)$
is an abelian group with an involution w,
$C(G/e)$
is an abelian group with an involution w,
![]() $C(G/G)$
is an abelian group with the trivial involution,
$C(G/G)$
is an abelian group with the trivial involution,
![]() $\mathrm {res}$
and
$\mathrm {res}$
and
![]() $\mathrm {tran}$
are homomorphisms of abelian groups with involutions, and the equality
$\mathrm {tran}$
are homomorphisms of abelian groups with involutions, and the equality
is satisfied (i.e. the double coset formula holds). A morphism of Mackey functors
![]() $C\to D$
is a diagram of abelian groups with involutions
$C\to D$
is a diagram of abelian groups with involutions

such that the horizontal homomorphisms commute with
![]() $\mathrm {tran}$
and
$\mathrm {tran}$
and
![]() $\mathrm {res}$
.
$\mathrm {res}$
.
Example 2.2.2. If M is an abelian group with involution, then we can associate the Mackey functor

where
![]() $\mathrm {tran}$
maps
$\mathrm {tran}$
maps
![]() $x\in M$
to
$x\in M$
to
![]() $x+w(x)$
, and
$x+w(x)$
, and
![]() $\mathrm {res}$
is the inclusion. In this way, we obtain a fully faithful functor from the category of abelian groups with involutions to the category of Mackey functors
$\mathrm {res}$
is the inclusion. In this way, we obtain a fully faithful functor from the category of abelian groups with involutions to the category of Mackey functors
![]() $\mathrm {Mack}_{{\mathbb {Z}/2}}$
. We often regard an abelian group with involution as a Mackey functor if no confusion seems likely to arise.
$\mathrm {Mack}_{{\mathbb {Z}/2}}$
. We often regard an abelian group with involution as a Mackey functor if no confusion seems likely to arise.
Lemma 2.2.3. Let A be a Green functor for
![]() $G:={\mathbb {Z}/2}$
, and let M and L are A-modules. If L is associated (in the sense of the previous example) with an abelian group with involution, then the induced map
$G:={\mathbb {Z}/2}$
, and let M and L are A-modules. If L is associated (in the sense of the previous example) with an abelian group with involution, then the induced map
is an isomorphism.
Proof. Let
![]() $f\colon M(G/e)\to L(G/e)$
be a homomorphism of
$f\colon M(G/e)\to L(G/e)$
be a homomorphism of
![]() $A(G/e)$
-modules. Then the image of
$A(G/e)$
-modules. Then the image of
![]() $f\circ \mathrm {res}$
is in
$f\circ \mathrm {res}$
is in
![]() $L(G/e)^{{\mathbb {Z}/2}}$
. Hence, there exists a unique homomorphism of
$L(G/e)^{{\mathbb {Z}/2}}$
. Hence, there exists a unique homomorphism of
![]() $A(G/G)$
-modules
$A(G/G)$
-modules
![]() $g\colon M(G/G)\to L(G/G)$
such that in the diagram
$g\colon M(G/G)\to L(G/G)$
such that in the diagram

the pair
![]() $(f,g)$
commutes with
$(f,g)$
commutes with
![]() $\mathrm {res}$
. We have
$\mathrm {res}$
. We have
Since
![]() $\mathrm {res}$
for L is injective, we deduce that the pair
$\mathrm {res}$
for L is injective, we deduce that the pair
![]() $(f,g)$
commutes with
$(f,g)$
commutes with
![]() $\mathrm {tran}$
. This constructs an inverse of equation (2.6).
$\mathrm {tran}$
. This constructs an inverse of equation (2.6).
2.3 Equivariant Eilenberg–MacLane spectra
In this subsection, we explain basic properties of equivariant Eilenberg–MacLane spectra. We also explain how to define
![]() $\mathrm {THR}$
of commutative rings.
$\mathrm {THR}$
of commutative rings.
Definition 2.3.1. Let
![]() $\mathcal {C}$
be a category (not an
$\mathcal {C}$
be a category (not an
![]() $\infty $
-category). We have the functors
$\infty $
-category). We have the functors
induced by (2.1). Let
![]() $(-)^{{\mathbb {Z}/2}}$
denote the right adjoint of
$(-)^{{\mathbb {Z}/2}}$
denote the right adjoint of
![]() $\iota $
if it exists.
$\iota $
if it exists.
Here, we give some examples. For a commutative ring A,
![]() $\iota A$
is the commutative ring A with the trivial involution. For an A-module M,
$\iota A$
is the commutative ring A with the trivial involution. For an A-module M,
![]() $\iota M$
is the
$\iota M$
is the
![]() $\iota A$
-module M with the trivial involution. By abuse of notation we sometimes denote the constant Mackey functors by
$\iota A$
-module M with the trivial involution. By abuse of notation we sometimes denote the constant Mackey functors by
![]() $\iota A$
and
$\iota A$
and
![]() $\iota M$
as well.
$\iota M$
as well.
For a commutative ring B with involution,
![]() $i^*B$
is the commutative ring obtained by forgetting the involution, and
$i^*B$
is the commutative ring obtained by forgetting the involution, and
![]() $B^{{\mathbb {Z}/2}}$
is the
$B^{{\mathbb {Z}/2}}$
is the
![]() ${\mathbb {Z}/2}$
-fixed point ring. For a B-module L,
${\mathbb {Z}/2}$
-fixed point ring. For a B-module L,
![]() $i^*L$
is the
$i^*L$
is the
![]() $i^*B$
-module obtained by forgetting the involution.
$i^*B$
-module obtained by forgetting the involution.
Definition 2.3.2. For an abelian group M with involution, we regard M as a Mackey functor, and take the functor (A.25) to obtain the equivariant Eilenberg–MacLane spectrum
![]() $\mathrm {H} M$
. There are canonical equivalences
$\mathrm {H} M$
. There are canonical equivalences
For a commutative ring A with involution, we can regard
![]() $\mathrm {H} A$
as an object of
$\mathrm {H} A$
as an object of
![]() $\mathrm {NAlg}_{{\mathbb {Z}/2}}$
as explained in [Reference Schwede53, Example 11.12].
$\mathrm {NAlg}_{{\mathbb {Z}/2}}$
as explained in [Reference Schwede53, Example 11.12].
Note that for a given commutative ring B the commutative ring spectra
![]() $\mathrm {H} \iota B$
and
$\mathrm {H} \iota B$
and
![]() $\iota \mathrm {H} B$
are quite different. For example, applying
$\iota \mathrm {H} B$
are quite different. For example, applying
![]() $\underline {\pi }_0$
to the first one yields the constant Mackey functor associated with B whereas for the second one a tensor product over
$\underline {\pi }_0$
to the first one yields the constant Mackey functor associated with B whereas for the second one a tensor product over
![]() $\mathbb {Z}$
with the Burnside ring Mackey functor of
$\mathbb {Z}$
with the Burnside ring Mackey functor of
![]() ${\mathbb {Z}/2}$
appears.
${\mathbb {Z}/2}$
appears.
Proposition 2.3.3. Let M be an abelian group. Then there is a canonical equivalence
where
![]() $M^{\oplus {\mathbb {Z}/2}}$
denotes the abelian group
$M^{\oplus {\mathbb {Z}/2}}$
denotes the abelian group
![]() $M\oplus M$
with the involution given by
$M\oplus M$
with the involution given by
![]() $(x,y)\mapsto (y,x)$
. The equivalence (2.8) can be promoted to an equivalence in
$(x,y)\mapsto (y,x)$
. The equivalence (2.8) can be promoted to an equivalence in
![]() $\mathrm {NAlg}_{{\mathbb {Z}/2}}$
if M is a commutative ring.
$\mathrm {NAlg}_{{\mathbb {Z}/2}}$
if M is a commutative ring.
Proof. There is an equivalence
by equation (2.7). Compose this with the map
![]() $\mathrm {H}(M\oplus M)\to \mathrm {H} M$
induced by the summation homomorphism
$\mathrm {H}(M\oplus M)\to \mathrm {H} M$
induced by the summation homomorphism
![]() $M\oplus M \to M$
, and then we construct equation (2.8) by adjunction. We need to show that the induced map
$M\oplus M \to M$
, and then we construct equation (2.8) by adjunction. We need to show that the induced map
is an isomorphism for
![]() $X={\mathbb {Z}/2},e$
and integer
$X={\mathbb {Z}/2},e$
and integer
![]() $n\in \mathbb {Z}$
. If
$n\in \mathbb {Z}$
. If
![]() $n\neq 0$
, then both sides are vanishing. Assume
$n\neq 0$
, then both sides are vanishing. Assume
![]() $n=0$
. More concretely, it remains to show that the composite of the induced maps
$n=0$
. More concretely, it remains to show that the composite of the induced maps
 $$ \begin{align} \begin{aligned} \operatorname{\mathrm{Hom}}_{\mathrm{Ho}(\mathrm{Sp}_{{\mathbb{Z}/2}})}(\Sigma^{\infty} X_+,\mathrm{H}(M^{\oplus {\mathbb{Z}/2}})) \to &\operatorname{\mathrm{Hom}}_{\mathrm{Ho}(\mathrm{Sp})}(i^*\Sigma^{\infty} X_+,i^*\mathrm{H}(M^{\oplus {\mathbb{Z}/2}}))\\ \to &\operatorname{\mathrm{Hom}}_{\mathrm{Ho}(\mathrm{Sp})}(i^*\Sigma^{\infty} X_+,\mathrm{H} M) \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \operatorname{\mathrm{Hom}}_{\mathrm{Ho}(\mathrm{Sp}_{{\mathbb{Z}/2}})}(\Sigma^{\infty} X_+,\mathrm{H}(M^{\oplus {\mathbb{Z}/2}})) \to &\operatorname{\mathrm{Hom}}_{\mathrm{Ho}(\mathrm{Sp})}(i^*\Sigma^{\infty} X_+,i^*\mathrm{H}(M^{\oplus {\mathbb{Z}/2}}))\\ \to &\operatorname{\mathrm{Hom}}_{\mathrm{Ho}(\mathrm{Sp})}(i^*\Sigma^{\infty} X_+,\mathrm{H} M) \end{aligned} \end{align} $$
is an isomorphism.
If
![]() $X={\mathbb {Z}/2}$
, then equation (2.10) can be written as the homomorphisms
$X={\mathbb {Z}/2}$
, then equation (2.10) can be written as the homomorphisms
given by
![]() $(x,y)\mapsto (x,0,y,0)$
and
$(x,y)\mapsto (x,0,y,0)$
and
![]() $(x,y,z,w)\mapsto (x+y,z+w)$
. The composite is an isomorphism. If
$(x,y,z,w)\mapsto (x+y,z+w)$
. The composite is an isomorphism. If
![]() $X=e$
, then equation (2.10) can be written as the homomorphisms
$X=e$
, then equation (2.10) can be written as the homomorphisms
given by
![]() $x\mapsto (x,0)$
and
$x\mapsto (x,0)$
and
![]() $(x,y)\mapsto x+y$
. The composite is also an isomorphism.
$(x,y)\mapsto x+y$
. The composite is also an isomorphism.
If M is a commutative ring, then equation (2.9) is an equivalence in
![]() $\mathrm {NAlg}_{{\mathbb {Z}/2}}$
. Hence, we obtain equation (2.8) as an equivalence in
$\mathrm {NAlg}_{{\mathbb {Z}/2}}$
. Hence, we obtain equation (2.8) as an equivalence in
![]() $\mathrm {NAlg}_{{\mathbb {Z}/2}}$
.
$\mathrm {NAlg}_{{\mathbb {Z}/2}}$
.
Definition 2.3.4. For a commutative ring A with involution, we set
From the map (2.3), we see that
![]() $\mathrm {THR}(A)$
is an
$\mathrm {THR}(A)$
is an
![]() $\mathrm {H} A$
-module.
$\mathrm {H} A$
-module.
Recall from equation (A.18) that
![]() $\underline {\pi }_0$
of an equivariant spectrum is a Mackey functor.
$\underline {\pi }_0$
of an equivariant spectrum is a Mackey functor.
Proposition 2.3.5. For every commutative ring A, the morphism of Mackey functors
induced by equation (2.3) is an isomorphism.
Proof. By [Reference Dotto, Moi, Patchkoria and Reeh16, Theorem 5.1], the morphism (2.11) can be described as a diagram

where
![]() $\alpha (x)=1\otimes x$
for
$\alpha (x)=1\otimes x$
for
![]() $x\in A$
, and T is the subgroup generated by
$x\in A$
, and T is the subgroup generated by
![]() $ax\otimes b-a\otimes xb$
for
$ax\otimes b-a\otimes xb$
for
![]() $a,b,x\in A$
. The description of T means that
$a,b,x\in A$
. The description of T means that
![]() $\alpha $
is an isomorphism. It follows that equation (2.11) is an isomorphism.
$\alpha $
is an isomorphism. It follows that equation (2.11) is an isomorphism.
2.4 Norm functors and flat modules
The purpose of this subsection is to prove Proposition 2.4.2, which is one ingredient of the proof of Theorem 3.2.3.
Definition 2.4.1. Suppose A is a commutative ring and M is an A-module. Let
![]() $N_A^{{\mathbb {Z}/2}} M$
denote the
$N_A^{{\mathbb {Z}/2}} M$
denote the
![]() $\iota A$
-module
$\iota A$
-module
![]() $M\otimes _A M$
whose
$M\otimes _A M$
whose
![]() ${\mathbb {Z}/2}$
-action is given by
${\mathbb {Z}/2}$
-action is given by
![]() $a\otimes b\mapsto b\otimes a$
. If
$a\otimes b\mapsto b\otimes a$
. If
![]() $A=\mathbb {Z}$
, we simply write
$A=\mathbb {Z}$
, we simply write
![]() $N^{{\mathbb {Z}/2}}M$
instead of
$N^{{\mathbb {Z}/2}}M$
instead of
![]() $N_{\mathbb {Z}}^{{\mathbb {Z}/2}}M$
.
$N_{\mathbb {Z}}^{{\mathbb {Z}/2}}M$
.
Observe that there is an isomorphism
![]() $N_A^{{\mathbb {Z}/2}} A\cong \iota A$
of commutative rings with involutions. We prefer to use the notation
$N_A^{{\mathbb {Z}/2}} A\cong \iota A$
of commutative rings with involutions. We prefer to use the notation
![]() $\iota A$
instead of
$\iota A$
instead of
![]() $N_A^{{\mathbb {Z}/2}}A$
for brevity.
$N_A^{{\mathbb {Z}/2}}A$
for brevity.
Proposition 2.4.2. Let M be an A-module, where A is a commutative ring. Then there exists a canonical map of
![]() $\mathrm {H} \iota A$
-modules
$\mathrm {H} \iota A$
-modules
If M is flat, then this map is an equivalence.
Proof. First, we have a map
![]() $N^{{\mathbb {Z}/2}} \mathrm {H} A \to \mathrm {H} \iota A$
using the adjunction
$N^{{\mathbb {Z}/2}} \mathrm {H} A \to \mathrm {H} \iota A$
using the adjunction
![]() $(N^{{\mathbb {Z}/2}},i^*)$
, that
$(N^{{\mathbb {Z}/2}},i^*)$
, that
![]() $i^*$
commutes with
$i^*$
commutes with
![]() $\mathrm {H}$
and that
$\mathrm {H}$
and that
![]() $i^*\iota \simeq id$
. We have the
$i^*\iota \simeq id$
. We have the
![]() $\iota A$
-module structure on
$\iota A$
-module structure on
![]() $N_A^{{\mathbb {Z}/2}} M$
given by
$N_A^{{\mathbb {Z}/2}} M$
given by
![]() $a(x\otimes y)=ax\otimes y$
for all
$a(x\otimes y)=ax\otimes y$
for all
![]() $a\in A$
and
$a\in A$
and
![]() $x\otimes y\in N_A^{{\mathbb {Z}/2}} M$
. Hence, we can regard
$x\otimes y\in N_A^{{\mathbb {Z}/2}} M$
. Hence, we can regard
![]() $\mathrm {H}(N_A^{{\mathbb {Z}/2}} M)$
as an
$\mathrm {H}(N_A^{{\mathbb {Z}/2}} M)$
as an
![]() $\mathrm {H} \iota A$
-module. By [Reference Lurie42, Proposition 4.6.2.17], to construct equation (2.12), it suffices to construct a map of
$\mathrm {H} \iota A$
-module. By [Reference Lurie42, Proposition 4.6.2.17], to construct equation (2.12), it suffices to construct a map of
![]() $N^{{\mathbb {Z}/2}}\mathrm {H} A$
-modules
$N^{{\mathbb {Z}/2}}\mathrm {H} A$
-modules
By Proposition Appendix A.3.7,
![]() $N^{{\mathbb {Z}/2}}\mathrm {H} A$
and
$N^{{\mathbb {Z}/2}}\mathrm {H} A$
and
![]() $N^{{\mathbb {Z}/2}} \mathrm {H} M$
are
$N^{{\mathbb {Z}/2}} \mathrm {H} M$
are
![]() $(-1)$
-connected. From the adjoint pairs (A.27) and (A.29), we obtain a map in
$(-1)$
-connected. From the adjoint pairs (A.27) and (A.29), we obtain a map in
![]() $\mathrm {CAlg}_{\mathbb {Z}/2}$
$\mathrm {CAlg}_{\mathbb {Z}/2}$
and a map of
![]() $N^{{\mathbb {Z}/2}}\mathrm {H} A$
-modules
$N^{{\mathbb {Z}/2}}\mathrm {H} A$
-modules
Hence, to construct equation (2.13), it suffices to construct a map of
![]() $\underline {\pi }_0(N^{{\mathbb {Z}/2}} \mathrm {H} A)$
-modules
$\underline {\pi }_0(N^{{\mathbb {Z}/2}} \mathrm {H} A)$
-modules
By Lemma 2.2.3 and Definition 2.4.1, this is equivalent to constructing a morphism of
![]() $\pi _0(i^*N^{{\mathbb {Z}/2}}\mathrm {H} A)$
-modules
$\pi _0(i^*N^{{\mathbb {Z}/2}}\mathrm {H} A)$
-modules
that is, a morphism of
![]() $A\otimes A$
-modules
$A\otimes A$
-modules
![]() $M\otimes M\to M\otimes _A M$
since
$M\otimes M\to M\otimes _A M$
since
![]() $i^*N^{{\mathbb {Z}/2}}\simeq (-)^{\wedge 2}$
by Proposition Appendix A.2.7(6). The canonical assignment
$i^*N^{{\mathbb {Z}/2}}\simeq (-)^{\wedge 2}$
by Proposition Appendix A.2.7(6). The canonical assignment
![]() $x\otimes y\to x\otimes y$
finishes the construction.
$x\otimes y\to x\otimes y$
finishes the construction.
The class of A-modules such that equation (2.12) is an equivalence is closed under filtered colimits. By Lazard’s theorem, every flat A-module is a filtered colimit of finitely generated free A-modules. Hence, to show that equation (2.12) is an equivalence if M is flat, we may assume
![]() $M=A^n$
. In this case, there is an equivalence
$M=A^n$
. In this case, there is an equivalence
where
![]() $V_n$
is the set
$V_n$
is the set
![]() $[n]\times [n]$
with the
$[n]\times [n]$
with the
![]() ${\mathbb {Z}/2}$
-action given by
${\mathbb {Z}/2}$
-action given by
![]() $(a,b)\mapsto (b,a)$
. Hence, we obtain equivalences
$(a,b)\mapsto (b,a)$
. Hence, we obtain equivalences
Combining this with equation (2.12), we obtain a map
To show that f is an equivalence, it suffices to show that
![]() $\underline {\pi }_0(f)$
is an equivalence. Since
$\underline {\pi }_0(f)$
is an equivalence. Since
![]() $V_n \times \iota A$
and
$V_n \times \iota A$
and
![]() $N_A^{{\mathbb {Z}/2}} A^n$
are rings with involutions, by Lemma 2.2.3 it suffices to show that
$N_A^{{\mathbb {Z}/2}} A^n$
are rings with involutions, by Lemma 2.2.3 it suffices to show that
![]() $\pi _0(f)$
is an equivalence of modules over rings with involution. Hence, to show that equation (2.12) is an equivalence, it suffices to show that it is an equivalence after applying
$\pi _0(f)$
is an equivalence of modules over rings with involution. Hence, to show that equation (2.12) is an equivalence, it suffices to show that it is an equivalence after applying
![]() $\pi _0$
, that is, the induced map
$\pi _0$
, that is, the induced map
is an isomorphism. From the description of equation (2.14), we see that g is given by
for
![]() $x,y\in M$
and
$x,y\in M$
and
![]() $a\in A$
. One can readily check that this g is an isomorphism.
$a\in A$
. One can readily check that this g is an isomorphism.
3 Descent properties of THR
3.1 Some equivariant topologies
We refer to [Reference Heller, Krishna and Østvær26] for the definition of the stable
![]() ${\mathbb {Z}/2}$
-equivariant motivic homotopy category
${\mathbb {Z}/2}$
-equivariant motivic homotopy category
![]() $\mathcal {SH}^{\mathbb {Z}/2}(k)$
, which is compatible with the later work of Hoyois [Reference Hoyois33], but differs from Hermann’s [Reference Herrmann27]. See his Corollary 2.13 and Example 3.1, as well as [Reference Heller, Krishna and Østvær26, Example 2.16 and section 6.1], for a comparison. The following definitions are taken from [Reference Heller, Krishna and Østvær26]. Throughout this section, we assume that G is an abstract finite group, which we will identify with its associated finite group scheme over a fixed base scheme. We are mostly interested in the case
$\mathcal {SH}^{\mathbb {Z}/2}(k)$
, which is compatible with the later work of Hoyois [Reference Hoyois33], but differs from Hermann’s [Reference Herrmann27]. See his Corollary 2.13 and Example 3.1, as well as [Reference Heller, Krishna and Østvær26, Example 2.16 and section 6.1], for a comparison. The following definitions are taken from [Reference Heller, Krishna and Østvær26]. Throughout this section, we assume that G is an abstract finite group, which we will identify with its associated finite group scheme over a fixed base scheme. We are mostly interested in the case
![]() $G={\mathbb {Z}/2}=C_2$
.
$G={\mathbb {Z}/2}=C_2$
.
Definition 3.1.1. Let x be a point of a G-scheme X. The set-theoretic stabilizer of X at x is defined to be
The scheme-theoretic stabilizer of X at x is defined to be
Let
![]() $f\colon Y\to X$
be an equivariant morphism of G-schemes. We say that
$f\colon Y\to X$
be an equivariant morphism of G-schemes. We say that
-
(i) f is (equivariant) étale if its underlying morphism of schemes is étale,
-
(ii) f is an equivariant étale cover if f is étale and surjective,
-
(iii) f is isovariant if for every point
 $y\in Y$
, the induced homomorphism
$y\in Y$
, the induced homomorphism
 $G_y\to G_{f(y)}$
is an isomorphism,
$G_y\to G_{f(y)}$
is an isomorphism, -
(iv) f is an isovariant étale cover if f is isovariant and an equivariant étale cover,
-
(v) f is a fixed point étale cover if it is an étale cover and for every point
 $x\in X$
, there exists a point
$x\in X$
, there exists a point
 $y\in f^{-1}(x)$
such that
$y\in f^{-1}(x)$
such that
 $G_x\simeq G_y$
,
$G_x\simeq G_y$
, -
(vi) f is a equivariant Nisnevich cover if f is an étale cover and for every point
 $x\in X$
, there exists a point
$x\in X$
, there exists a point
 $y\in f^{-1}(x)$
such that
$y\in f^{-1}(x)$
such that
 $k(x)\simeq k(y)$
and
$k(x)\simeq k(y)$
and
 $S_x\simeq S_y$
.
$S_x\simeq S_y$
.
These covers define equivariant étale, isovariant étale, fixed point étale and equivariant Nisnevich topologies on the category of G-schemes.
The isovariant étale topology was first studied by Thomason [Reference Thomason56]; see, for example, [Reference Heller, Krishna and Østvær26, section 6.1]. By [Reference Rydh51, Remark 3.1], isovariant is the same as ‘fixed-point reflecting’, compare Definition 3.3 of loc. cit. The equivariant Nisnevich topology is due to Voevodsky [Reference Deligne13].
The discussion in [Reference Heller, Krishna and Østvær26, p. 1223] shows that the equivariant Nisnevich topology is coarser than the fixed point étale topology. As observed in the proof of [Reference Heller, Krishna and Østvær26, Corollary 6.6], the fixed point étale topology is equivalent to the isovariant étale topology. Hence, we have the following inclusions of topologies:
 $$ \begin{align*} \text{(equivariant Nisnevich)}\subset &\text{(fixed point}\ \acute{\mathrm{e}}\text{tale)} \\ \simeq &\text{(isovariant}\ \acute{\mathrm{e}}\text{tale)} \subset \text{(equivariant}\ \acute{\mathrm{e}}\text{tale).} \end{align*} $$
$$ \begin{align*} \text{(equivariant Nisnevich)}\subset &\text{(fixed point}\ \acute{\mathrm{e}}\text{tale)} \\ \simeq &\text{(isovariant}\ \acute{\mathrm{e}}\text{tale)} \subset \text{(equivariant}\ \acute{\mathrm{e}}\text{tale).} \end{align*} $$
For a G-scheme X, let
![]() $X/G$
denote the geometric quotient, which is an algebraic space. For the existence, see, for example, [Reference Rydh51, Corollary 5.4]. If S is a locally noetherian scheme with the trivial G-action and
$X/G$
denote the geometric quotient, which is an algebraic space. For the existence, see, for example, [Reference Rydh51, Corollary 5.4]. If S is a locally noetherian scheme with the trivial G-action and
![]() $X\to S$
is a quasi-projective G-equivariant morphism, then
$X\to S$
is a quasi-projective G-equivariant morphism, then
![]() $X/G$
is representable by an S-scheme according to [Reference Demazure and Grothendieck14, Théorème V.7.1]. If A is a commutative ring with G-action, then there is a canonical isomorphism
$X/G$
is representable by an S-scheme according to [Reference Demazure and Grothendieck14, Théorème V.7.1]. If A is a commutative ring with G-action, then there is a canonical isomorphism
![]() $\operatorname {\mathrm {Spec}}(A)/G\simeq \operatorname {\mathrm {Spec}}(A^G)$
; see, for example, [Reference Rydh51, Theorem 4.1].
$\operatorname {\mathrm {Spec}}(A)/G\simeq \operatorname {\mathrm {Spec}}(A^G)$
; see, for example, [Reference Rydh51, Theorem 4.1].
Proposition 3.1.2. Let
![]() $f\colon Y\to X$
be a separated isovariant étale morphism of G-schemes. Then the quotient morphism
$f\colon Y\to X$
be a separated isovariant étale morphism of G-schemes. Then the quotient morphism
![]() $Y/G\to X/G$
of algebraic spaces is étale, and the induced square
$Y/G\to X/G$
of algebraic spaces is étale, and the induced square

is Cartesian.
Proof. This appears on [Reference Heller, Krishna and Østvær26, p. 1225].
Definition 3.1.3. For a G-scheme X, let
![]() $X_{iso{\acute {e}t}}$
denote the small isovariant étale site with the isovariant étale coverings
$X_{iso{\acute {e}t}}$
denote the small isovariant étale site with the isovariant étale coverings
![]() $Y\to X$
of G-schemes.
$Y\to X$
of G-schemes.
Proposition 3.1.4 (Thomason).
Let X be a G-scheme. Then there exists an equivalence of sites
sending any
![]() $X/G$
-scheme Y to
$X/G$
-scheme Y to
![]() $Y\times _{X/G} X$
.
$Y\times _{X/G} X$
.
Proof. We refer to [Reference Heller, Krishna and Østvær26, Proposition 6.11].
Definition 3.1.5. Let X be a separated G-scheme. The presheaf
![]() $X^G$
on the category of separated schemes
$X^G$
on the category of separated schemes
![]() $\mathbf {Sch}$
is defined to be
$\mathbf {Sch}$
is defined to be
for
![]() $Y\in \mathbf {Sch}$
. By [Reference Demazure and Grothendieck14, Proposition 9.2 in Exposé XII],
$Y\in \mathbf {Sch}$
. By [Reference Demazure and Grothendieck14, Proposition 9.2 in Exposé XII],
![]() $X^G$
is representable by a closed subscheme of X. Furthermore, the points of the topological space underlying the scheme
$X^G$
is representable by a closed subscheme of X. Furthermore, the points of the topological space underlying the scheme
![]() $X^G$
are in canonical bijection with the points of the topological space of fixed points (recall G is finite).
$X^G$
are in canonical bijection with the points of the topological space of fixed points (recall G is finite).
3.2 Isovariant étale base change
Lemma 3.2.1. Let
![]() $A\to B$
be an étale homomorphism of commutative rings. Then the map
$A\to B$
be an étale homomorphism of commutative rings. Then the map
![]() $\mathrm {H}(m)\colon \mathrm {H}(N_A^{{\mathbb {Z}/2}} B)\to \mathrm {H}(\iota B)$
induced by the multiplication map
$\mathrm {H}(m)\colon \mathrm {H}(N_A^{{\mathbb {Z}/2}} B)\to \mathrm {H}(\iota B)$
induced by the multiplication map
is flat.
Proof. Let C be the kernel of m, which is an ideal of
![]() $B\otimes _A B$
with the induced involution. Since
$B\otimes _A B$
with the induced involution. Since
![]() $A\to B$
is étale, the diagonal morphism of schemes
$A\to B$
is étale, the diagonal morphism of schemes
![]() $\operatorname {\mathrm {Spec}}(B)\to \operatorname {\mathrm {Spec}}(B)\times _{\operatorname {\mathrm {Spec}}(A)}\operatorname {\mathrm {Spec}}(B)$
is an open and closed immersion by the implication a)
$\operatorname {\mathrm {Spec}}(B)\to \operatorname {\mathrm {Spec}}(B)\times _{\operatorname {\mathrm {Spec}}(A)}\operatorname {\mathrm {Spec}}(B)$
is an open and closed immersion by the implication a)
![]() $\Rightarrow $
b) in [Reference Dieudonné and Grothendieck15, Corollaire IV.17.4.2]. This implies that the ring structure on
$\Rightarrow $
b) in [Reference Dieudonné and Grothendieck15, Corollaire IV.17.4.2]. This implies that the ring structure on
![]() $B\otimes _A B$
makes a ring structure on C. Hence, we have an isomorphism of commutative rings with involutions
$B\otimes _A B$
makes a ring structure on C. Hence, we have an isomorphism of commutative rings with involutions
![]() $N_A^{{\mathbb {Z}/2}}B\cong \iota B\times C$
. We set
$N_A^{{\mathbb {Z}/2}}B\cong \iota B\times C$
. We set
![]() $e:=(1.0)\in \iota B\times C$
. There is an isomorphism
$e:=(1.0)\in \iota B\times C$
. There is an isomorphism
![]() $N_A^{{\mathbb {Z}/2}}B[1/e]\cong \iota B$
, which gives an isomorphism
$N_A^{{\mathbb {Z}/2}}B[1/e]\cong \iota B$
, which gives an isomorphism
Hence,
![]() $\iota B$
is a filtered colimit of free
$\iota B$
is a filtered colimit of free
![]() $N_A^{{\mathbb {Z}/2}}B$
-modules. By Proposition Appendix A.5.11, m is flat. It follows that
$N_A^{{\mathbb {Z}/2}}B$
-modules. By Proposition Appendix A.5.11, m is flat. It follows that
![]() $\mathrm {H}(m)$
is flat too.
$\mathrm {H}(m)$
is flat too.
Let
![]() $A\to B$
be a map in
$A\to B$
be a map in
![]() $\mathrm {NAlg}_{{\mathbb {Z}/2}}$
. Then we have the commutative square in
$\mathrm {NAlg}_{{\mathbb {Z}/2}}$
. Then we have the commutative square in
![]() $\mathrm {NAlg}_{{\mathbb {Z}/2}}$
$\mathrm {NAlg}_{{\mathbb {Z}/2}}$

where the horizontal maps are given by equation (2.3). Hence, we obtain an induced map
in
![]() $\mathrm {NAlg}_{{\mathbb {Z}/2}}$
. We will now study this map for
$\mathrm {NAlg}_{{\mathbb {Z}/2}}$
. We will now study this map for
![]() $\mathrm {H} \iota A \to \mathrm {H} \iota B$
.
$\mathrm {H} \iota A \to \mathrm {H} \iota B$
.
Note that the following result does not directly follow from the étale base change result [Reference Geisser and Hesselholt21, Proposition 3.2.1] for
![]() ${\mathrm {THH}}$
as neither
${\mathrm {THH}}$
as neither
![]() $\mathrm {H}$
nor
$\mathrm {H}$
nor
![]() $\mathrm {THR}$
commute with
$\mathrm {THR}$
commute with
![]() $\iota $
. This result is crucial for the descent results further below.
$\iota $
. This result is crucial for the descent results further below.
Proposition 3.2.2. Let
![]() $A\to B$
be an étale homomorphism of commutative rings. Then we have an induced equivalence
$A\to B$
be an étale homomorphism of commutative rings. Then we have an induced equivalence
Proof. Consider the commutative square

where the horizontal maps are induced by the map
![]() $A\to B$
, the vertical equivalences are obtained by Proposition 2.4.2 and the right-hand one even comes from the algebraic isomorphism mentioned after Definition 2.4.1. We have an equivalence
$A\to B$
, the vertical equivalences are obtained by Proposition 2.4.2 and the right-hand one even comes from the algebraic isomorphism mentioned after Definition 2.4.1. We have an equivalence
![]() $H\iota B\wedge _{N^{{\mathbb {Z}/2}} \mathrm {H} B} \mathrm {H} \iota B \simeq \mathrm {THR}(\iota B)$
. (This equivalence involves a computation for the index under the
$H\iota B\wedge _{N^{{\mathbb {Z}/2}} \mathrm {H} B} \mathrm {H} \iota B \simeq \mathrm {THR}(\iota B)$
. (This equivalence involves a computation for the index under the
![]() $\wedge $
, namely
$\wedge $
, namely
![]() $i^*\mathrm {H}\iota B \simeq \mathrm {H} B$
, which follows from equation (2.7). The same equivalence is used when identifying the upper left entry in the square.) This implies that equation (3.2) is equivalent to the upper horizontal map of equation (3.3). Proposition Appendix A.5.5 and Lemma 3.2.1 show that the lower horizontal map of equation (3.3) is flat. Putting everything together, we deduce that the map (3.2) is flat.
$i^*\mathrm {H}\iota B \simeq \mathrm {H} B$
, which follows from equation (2.7). The same equivalence is used when identifying the upper left entry in the square.) This implies that equation (3.2) is equivalent to the upper horizontal map of equation (3.3). Proposition Appendix A.5.5 and Lemma 3.2.1 show that the lower horizontal map of equation (3.3) is flat. Putting everything together, we deduce that the map (3.2) is flat.
We will show that this map is an equivalence as claimed by applying Proposition Appendix A.5.6. By Proposition Appendix A.3.7,
![]() $N^{{\mathbb {Z}/2}} \mathrm {H} A$
and
$N^{{\mathbb {Z}/2}} \mathrm {H} A$
and
![]() $N^{{\mathbb {Z}/2}} \mathrm {H} B$
are
$N^{{\mathbb {Z}/2}} \mathrm {H} B$
are
![]() $(-1)$
-connected. Hence, we may use Proposition Appendix A.4.4, and are reduced to showing that the induced morphism
$(-1)$
-connected. Hence, we may use Proposition Appendix A.4.4, and are reduced to showing that the induced morphism
is an isomorphism. This follows easily from applying Proposition 2.3.5 to A and B.
We now establish isovariant étale base change for commutative rings with possibly nontrivial involution.
Theorem 3.2.3. Let
![]() $A\to B$
be an isovariant étale homomorphism of commutative rings with involutions. Then there are canonical equivalences in
$A\to B$
be an isovariant étale homomorphism of commutative rings with involutions. Then there are canonical equivalences in
![]() $\mathrm {NAlg}_{{\mathbb {Z}/2}}$
$\mathrm {NAlg}_{{\mathbb {Z}/2}}$
Proof. We have isomorphisms
![]() $\operatorname {\mathrm {Spec}}(A^{{\mathbb {Z}/2}})\simeq \operatorname {\mathrm {Spec}}(A)/({\mathbb {Z}/2})$
and
$\operatorname {\mathrm {Spec}}(A^{{\mathbb {Z}/2}})\simeq \operatorname {\mathrm {Spec}}(A)/({\mathbb {Z}/2})$
and
![]() $\operatorname {\mathrm {Spec}}(B^{{\mathbb {Z}/2}})\simeq \operatorname {\mathrm {Spec}}(B)/({\mathbb {Z}/2})$
. Hence, by Proposition 3.1.2, the induced homomorphism
$\operatorname {\mathrm {Spec}}(B^{{\mathbb {Z}/2}})\simeq \operatorname {\mathrm {Spec}}(B)/({\mathbb {Z}/2})$
. Hence, by Proposition 3.1.2, the induced homomorphism
![]() $A^{{\mathbb {Z}/2}}\to B^{{\mathbb {Z}/2}}$
is étale, and there is an isomorphism of commutative rings with involution
$A^{{\mathbb {Z}/2}}\to B^{{\mathbb {Z}/2}}$
is étale, and there is an isomorphism of commutative rings with involution
Since
![]() $A^{{\mathbb {Z}/2}}\to B^{{\mathbb {Z}/2}}$
is flat,
$A^{{\mathbb {Z}/2}}\to B^{{\mathbb {Z}/2}}$
is flat,
![]() $B^{{\mathbb {Z}/2}}$
is a filtered colimit of finite free
$B^{{\mathbb {Z}/2}}$
is a filtered colimit of finite free
![]() $A^{{\mathbb {Z}/2}}$
-modules. It follows that
$A^{{\mathbb {Z}/2}}$
-modules. It follows that
![]() $\iota A^{{\mathbb {Z}/2}}\to \iota B^{{\mathbb {Z}/2}}$
is flat by Proposition Appendix A.5.11. Hence, the isomorphism (3.4) induces an equivalence
$\iota A^{{\mathbb {Z}/2}}\to \iota B^{{\mathbb {Z}/2}}$
is flat by Proposition Appendix A.5.11. Hence, the isomorphism (3.4) induces an equivalence
![]() $\mathrm {H} B \simeq \mathrm {H} A \wedge _{\mathrm {H} (\iota A^{{\mathbb {Z}/2}})} \mathrm {H} (\iota B^{{\mathbb {Z}/2}})$
by Proposition Appendix A.5.7. Then Proposition 2.1.5 yields an equivalence
$\mathrm {H} B \simeq \mathrm {H} A \wedge _{\mathrm {H} (\iota A^{{\mathbb {Z}/2}})} \mathrm {H} (\iota B^{{\mathbb {Z}/2}})$
by Proposition Appendix A.5.7. Then Proposition 2.1.5 yields an equivalence
Now, Proposition 3.2.2 implies the left equivalence of the Proposition after canceling out one smash factor
![]() $\mathrm {THR}(\iota (A^{{\mathbb {Z}/2}}))$
. Applying the isovariance condition once more gives the right-hand side equivalence.
$\mathrm {THR}(\iota (A^{{\mathbb {Z}/2}}))$
. Applying the isovariance condition once more gives the right-hand side equivalence.
3.3 Presheaves of equivariant spectra
Zariski and other sheaves are completely determined by their behaviors on affine schemes. This is known to be true in some homotopical settings as well. The purpose of this section is to establish a rather general result, namely Proposition 3.3.13, which applies to our setting, that is the isovariant étale site and
![]() ${\mathbb {Z}/2}$
-equivariant spectra. For this, a result of [Reference Ayoub3] will be very useful.
${\mathbb {Z}/2}$
-equivariant spectra. For this, a result of [Reference Ayoub3] will be very useful.
Definition 3.3.1. Let
![]() $\mathcal {C}$
be a category with a Grothendieck topology t, and let
$\mathcal {C}$
be a category with a Grothendieck topology t, and let
![]() $\mathcal {V}$
be a presentable
$\mathcal {V}$
be a presentable
![]() $\infty $
-category. Let
$\infty $
-category. Let
denote the
![]() $\infty $
-category of presheaves on
$\infty $
-category of presheaves on
![]() $\mathcal {C}$
with values in
$\mathcal {C}$
with values in
![]() $\mathcal {V}$
. We say that a presheaf
$\mathcal {V}$
. We say that a presheaf
![]() $\mathcal {F}\in \mathcal {P}\mathrm {sh}(\mathcal {C},\mathcal {V})$
satisfies t-descent if the induced map
$\mathcal {F}\in \mathcal {P}\mathrm {sh}(\mathcal {C},\mathcal {V})$
satisfies t-descent if the induced map
is an equivalence for every t-hypercover
![]() $\mathscr {X}\to X$
. Let
$\mathscr {X}\to X$
. Let
![]() $\mathcal {S}\mathrm {hv}_t(\mathcal {C},\mathcal {V})$
denote the full subcategory of
$\mathcal {S}\mathrm {hv}_t(\mathcal {C},\mathcal {V})$
denote the full subcategory of
![]() $\mathcal {P}\mathrm {sh}(\mathcal {C},\mathcal {V})$
consisting of presheaves satisfying t-descent. We often omit t in the above notation if it is clear from the context.
$\mathcal {P}\mathrm {sh}(\mathcal {C},\mathcal {V})$
consisting of presheaves satisfying t-descent. We often omit t in the above notation if it is clear from the context.
The above condition is sometimes called t-hyperdescent, in order to distinguish it from the weaker descent condition only for covering sieves rather than all hypercovers. We refer to [Reference Lurie41, section 6.5] and [Reference Dugger, Hollander and Isaksen18] for a careful comparison.
If
![]() $\mathcal {V}\to \mathcal {V}'$
is a functor of
$\mathcal {V}\to \mathcal {V}'$
is a functor of
![]() $\infty $
-categories, then this induces a functor
$\infty $
-categories, then this induces a functor
![]() $\mathcal {P}\mathrm {sh}(\mathcal {C},\mathcal {V})\to \mathcal {P}\mathrm {sh}(\mathcal {C},\mathcal {V}')$
. In this way, we obtain functors
$\mathcal {P}\mathrm {sh}(\mathcal {C},\mathcal {V})\to \mathcal {P}\mathrm {sh}(\mathcal {C},\mathcal {V}')$
. In this way, we obtain functors
![]() $i^*$
,
$i^*$
,
![]() $(-)^{{\mathbb {Z}/2}}$
and so on for the presheaf categories.
$(-)^{{\mathbb {Z}/2}}$
and so on for the presheaf categories.
Proposition 3.3.2. Suppose
![]() $\mathcal {F}\in \mathcal {P}\mathrm {sh}(\mathcal {C},\mathrm {Sp}_{{\mathbb {Z}/2}})$
, where
$\mathcal {F}\in \mathcal {P}\mathrm {sh}(\mathcal {C},\mathrm {Sp}_{{\mathbb {Z}/2}})$
, where
![]() $\mathcal {C}$
is a site. Then
$\mathcal {C}$
is a site. Then
![]() $\mathcal {F}\in \mathcal {S}\mathrm {hv}(\mathcal {C},\mathrm {Sp}_{{\mathbb {Z}/2}})$
if and only if
$\mathcal {F}\in \mathcal {S}\mathrm {hv}(\mathcal {C},\mathrm {Sp}_{{\mathbb {Z}/2}})$
if and only if
![]() $i^*\mathcal {F},\mathcal {F}^{{\mathbb {Z}/2}}\in \mathcal {S}\mathrm {hv}(\mathcal {C},\mathrm {Sp})$
.
$i^*\mathcal {F},\mathcal {F}^{{\mathbb {Z}/2}}\in \mathcal {S}\mathrm {hv}(\mathcal {C},\mathrm {Sp})$
.
Proof. Let
![]() $\mathscr {X}\to X$
be a hypercover. Since
$\mathscr {X}\to X$
be a hypercover. Since
![]() $i^*$
and
$i^*$
and
![]() $(-)^{{\mathbb {Z}/2}}$
preserve limits, equation (3.5) is an equivalence if and only if
$(-)^{{\mathbb {Z}/2}}$
preserve limits, equation (3.5) is an equivalence if and only if
are equivalences. Equivalently,
![]() $i^*\mathcal {F},\mathcal {F}^{{\mathbb {Z}/2}}\in \mathcal {S}\mathrm {hv}(\mathcal {C},\mathrm {Sp})$
.
$i^*\mathcal {F},\mathcal {F}^{{\mathbb {Z}/2}}\in \mathcal {S}\mathrm {hv}(\mathcal {C},\mathrm {Sp})$
.
Definition 3.3.3. Let
![]() $\mathcal {C}$
be a site. As a consequence of Proposition 3.3.2, we see that
$\mathcal {C}$
be a site. As a consequence of Proposition 3.3.2, we see that
![]() $\mathcal {S}\mathrm {hv}(\mathcal {C},\mathrm {Sp}_{{\mathbb {Z}/2}})$
is the full subcategory of local objects of [Reference Lurie41, Definition 5.5.4.1] with respect to the class of maps consisting of
$\mathcal {S}\mathrm {hv}(\mathcal {C},\mathrm {Sp}_{{\mathbb {Z}/2}})$
is the full subcategory of local objects of [Reference Lurie41, Definition 5.5.4.1] with respect to the class of maps consisting of
for all hypercovers
![]() $\mathscr {X}\to X$
and integers n. In particular, there is an adjoint pair
$\mathscr {X}\to X$
and integers n. In particular, there is an adjoint pair
by [Reference Lurie41, Proposition 5.5.4.15(3)], where
![]() $\eta $
is the inclusion functor. A map
$\eta $
is the inclusion functor. A map
![]() $\mathcal {F}\to \mathcal {G}$
in
$\mathcal {F}\to \mathcal {G}$
in
![]() $\mathcal {P}\mathrm {sh}(\mathcal {C},\mathrm {Sp}_{{\mathbb {Z}/2}})$
is called a local equivalence if
$\mathcal {P}\mathrm {sh}(\mathcal {C},\mathrm {Sp}_{{\mathbb {Z}/2}})$
is called a local equivalence if
![]() $L\mathcal {F} \to L\mathcal {G}$
is an equivalence.
$L\mathcal {F} \to L\mathcal {G}$
is an equivalence.
Proposition 3.3.4. Let
![]() $\mathcal {C}$
be a site. Then the functor
$\mathcal {C}$
be a site. Then the functor
preserves local equivalences.
Proof. We need to show that the maps
are local equivalences for all hypercovers
![]() $\mathscr {X}\to X$
and integers n, which follow from Proposition Appendix A.2.7(2),(7).
$\mathscr {X}\to X$
and integers n, which follow from Proposition Appendix A.2.7(2),(7).
Proposition 3.3.5. Let
![]() $\mathcal {C}$
be a site. Then the functor
$\mathcal {C}$
be a site. Then the functor
preserves local equivalences.
Proof. We need to show that the maps
are local equivalences. Since
![]() $(-)^{{\mathbb {Z}/2}} i_{\sharp }\simeq (-)^{{\mathbb {Z}/2}} i_*\simeq \mathrm {id}$
by Proposition Appendix A.2.7(2),(3), the second map in equation (3.7) is an equivalence.
$(-)^{{\mathbb {Z}/2}} i_{\sharp }\simeq (-)^{{\mathbb {Z}/2}} i_*\simeq \mathrm {id}$
by Proposition Appendix A.2.7(2),(3), the second map in equation (3.7) is an equivalence.
The formulation (A.4) means that
![]() $\iota $
commutes with
$\iota $
commutes with
![]() $\Sigma ^{\infty }$
, and there is an equivalence
$\Sigma ^{\infty }$
, and there is an equivalence
![]() $(\iota X)^{{\mathbb {Z}/2}}\simeq X$
. Together with the tom Dieck splitting [Reference Greenlees and May23, Theorem 3.10], we have an equivalence
$(\iota X)^{{\mathbb {Z}/2}}\simeq X$
. Together with the tom Dieck splitting [Reference Greenlees and May23, Theorem 3.10], we have an equivalence
We have a similar equivalence for
![]() $\mathscr {X}$
too. Since
$\mathscr {X}$
too. Since
are local equivalences in
![]() $\mathcal {P}\mathrm {sh}(\mathcal {C},\mathrm {Sp})$
, the first map in equation (3.7) is a local equivalence.
$\mathcal {P}\mathrm {sh}(\mathcal {C},\mathrm {Sp})$
, the first map in equation (3.7) is a local equivalence.
Remark 3.3.6. Some of the results in this subsection including Propositions 3.3.2 and 3.3.4 have obvious generalizations to
![]() $\mathrm {Sp}_G$
for finite groups G. We also expect that Proposition 3.3.5 can be generalized too, but this should require extra effort since the tom Dieck splitting becomes more complicated.
$\mathrm {Sp}_G$
for finite groups G. We also expect that Proposition 3.3.5 can be generalized too, but this should require extra effort since the tom Dieck splitting becomes more complicated.
Proposition 3.3.7. Let
![]() $f\colon \mathcal {F}\to \mathcal {G}$
be a morphism in
$f\colon \mathcal {F}\to \mathcal {G}$
be a morphism in
![]() $\mathcal {P}\mathrm {sh}(\mathcal {C},\mathrm {Sp}_{{\mathbb {Z}/2}})$
, where
$\mathcal {P}\mathrm {sh}(\mathcal {C},\mathrm {Sp}_{{\mathbb {Z}/2}})$
, where
![]() $\mathcal {C}$
is a site. If
$\mathcal {C}$
is a site. If
![]() $i^*f$
and
$i^*f$
and
![]() $f^{{\mathbb {Z}/2}}$
are local equivalences, then f is a local equivalence.
$f^{{\mathbb {Z}/2}}$
are local equivalences, then f is a local equivalence.
Proof. By considering the fiber of f, we reduce to the case when
![]() $\mathcal {G}=0$
. This means that
$\mathcal {G}=0$
. This means that
![]() $i^*\mathcal {F}$
and
$i^*\mathcal {F}$
and
![]() $\mathcal {F}^{{\mathbb {Z}/2}}$
are local equivalent to
$\mathcal {F}^{{\mathbb {Z}/2}}$
are local equivalent to
![]() $0$
. The adjoint pair (2.4) gives a local equivalence
$0$
. The adjoint pair (2.4) gives a local equivalence
![]() $\mathcal {F}\to \mathcal {F}'$
with
$\mathcal {F}\to \mathcal {F}'$
with
![]() $\mathcal {F}'\in \mathcal {S}\mathrm {hv}(\mathcal {C},\mathrm {Sp}_{{\mathbb {Z}/2}})$
. By Propositions 3.3.4 and 3.3.5,
$\mathcal {F}'\in \mathcal {S}\mathrm {hv}(\mathcal {C},\mathrm {Sp}_{{\mathbb {Z}/2}})$
. By Propositions 3.3.4 and 3.3.5,
![]() $i^*\mathcal {F}'$
and
$i^*\mathcal {F}'$
and
![]() $\mathcal {F}^{\prime {\mathbb {Z}/2}}$
are local equivalent to
$\mathcal {F}^{\prime {\mathbb {Z}/2}}$
are local equivalent to
![]() $0$
. Since
$0$
. Since
![]() $i^*\mathcal {F}',\mathcal {F}^{\prime {\mathbb {Z}/2}}\in \mathcal {S}\mathrm {hv}(\mathcal {C},\mathrm {Sp})$
by Proposition 3.3.2, it follows that
$i^*\mathcal {F}',\mathcal {F}^{\prime {\mathbb {Z}/2}}\in \mathcal {S}\mathrm {hv}(\mathcal {C},\mathrm {Sp})$
by Proposition 3.3.2, it follows that
![]() $i^*\mathcal {F}'$
and
$i^*\mathcal {F}'$
and
![]() $\mathcal {F}^{\prime {\mathbb {Z}/2}}$
are equivalent to
$\mathcal {F}^{\prime {\mathbb {Z}/2}}$
are equivalent to
![]() $0$
. Hence,
$0$
. Hence,
![]() $\mathcal {F}'$
is equivalent to
$\mathcal {F}'$
is equivalent to
![]() $0$
, that is,
$0$
, that is,
![]() $\mathcal {F}$
is local equivalent to
$\mathcal {F}$
is local equivalent to
![]() $0$
.
$0$
.
Definition 3.3.8. Let
![]() $\mathfrak {M}$
be a combinatorial model category. For a category
$\mathfrak {M}$
be a combinatorial model category. For a category
![]() $\mathcal {C}$
, we set
$\mathcal {C}$
, we set
A morphism
![]() $\mathcal {F}\to \mathcal {G}$
in
$\mathcal {F}\to \mathcal {G}$
in
![]() $\mathbf {Psh}(\mathcal {C},\mathfrak {M})$
is a weak equivalence (resp. fibration) if
$\mathbf {Psh}(\mathcal {C},\mathfrak {M})$
is a weak equivalence (resp. fibration) if
![]() $\mathcal {F}(X)\to \mathcal {G}(X)$
is a weak equivalence (resp. fibration) for all
$\mathcal {F}(X)\to \mathcal {G}(X)$
is a weak equivalence (resp. fibration) for all
![]() $X\in \mathcal {C}$
. One can form a projective model structure based on these; see [Reference Ayoub3, Definition 4.4.18].
$X\in \mathcal {C}$
. One can form a projective model structure based on these; see [Reference Ayoub3, Definition 4.4.18].
If
![]() $\mathcal {V}$
is the underlying
$\mathcal {V}$
is the underlying
![]() $\infty $
-category of
$\infty $
-category of
![]() $\mathfrak {M}$
, then the underlying
$\mathfrak {M}$
, then the underlying
![]() $\infty $
-category of
$\infty $
-category of
![]() $\mathbf {Psh}(\mathcal {C},\mathfrak {M})$
with respect to the projective model structure is equivalent to
$\mathbf {Psh}(\mathcal {C},\mathfrak {M})$
with respect to the projective model structure is equivalent to
![]() $\mathcal {P}\mathrm {sh}(\mathcal {C},\mathcal {V})$
by [Reference Lurie42, Proposition 1.3.4.25].
$\mathcal {P}\mathrm {sh}(\mathcal {C},\mathcal {V})$
by [Reference Lurie42, Proposition 1.3.4.25].
Definition 3.3.9 ([Reference Ayoub3, Definition 4.4.23]).
A category of coefficients is a left proper cofibrantly generated stable model category
![]() $\mathfrak {M}$
satisfying the following conditions:
$\mathfrak {M}$
satisfying the following conditions:
-
(i) Finite coproducts of weak equivalences are weak equivalences.
-
(ii) There exists a set
 $\mathcal {E}$
of compact objects of
$\mathcal {E}$
of compact objects of
 $\mathfrak {M}$
that generates the homotopy category
$\mathfrak {M}$
that generates the homotopy category
 $\mathrm {Ho}(\mathfrak {M})$
.
$\mathrm {Ho}(\mathfrak {M})$
.
The set
![]() $\mathcal {E}$
is considered as a part of the data.
$\mathcal {E}$
is considered as a part of the data.
Example 3.3.10. According to [Reference Hill, Hopkins and Ravenel29, Proposition B.63],
![]() $\mathrm {Sp}^O_G$
is a cofibrantly generated stable model category. By [Reference Hill, Hopkins and Ravenel29, Example B.10, Remark B.64],
$\mathrm {Sp}^O_G$
is a cofibrantly generated stable model category. By [Reference Hill, Hopkins and Ravenel29, Example B.10, Remark B.64],
![]() $\mathrm {Sp}^O_G$
is left proper. A consequence of [Reference Hill, Hopkins and Ravenel29, Corollary B.43] is that finite coproducts of weak equivalences are weak equivalences. Let
$\mathrm {Sp}^O_G$
is left proper. A consequence of [Reference Hill, Hopkins and Ravenel29, Corollary B.43] is that finite coproducts of weak equivalences are weak equivalences. Let
![]() $\mathcal {E}$
be the set of
$\mathcal {E}$
be the set of
![]() $\Sigma ^n\Sigma ^{\infty } (G/H)_+$
for all subgroups H of G and integers n, which consists of compact objects and generates
$\Sigma ^n\Sigma ^{\infty } (G/H)_+$
for all subgroups H of G and integers n, which consists of compact objects and generates
![]() $\mathrm {Ho}(\mathrm {Sp}^O_G)$
by Proposition Appendix A.1.6. In conclusion,
$\mathrm {Ho}(\mathrm {Sp}^O_G)$
by Proposition Appendix A.1.6. In conclusion,
![]() $\mathrm {Sp}^O_G$
is a category of coefficients.
$\mathrm {Sp}^O_G$
is a category of coefficients.
We also note that
![]() $\mathrm {Sp}^O_G$
is a combinatorial model category.
$\mathrm {Sp}^O_G$
is a combinatorial model category.
Definition 3.3.11. Let
![]() $\mathcal {C}$
be a site. According to [Reference Ayoub3, Definition 4.4.28], a morphism
$\mathcal {C}$
be a site. According to [Reference Ayoub3, Definition 4.4.28], a morphism
![]() $\mathcal {F}\to \mathcal {G}$
in
$\mathcal {F}\to \mathcal {G}$
in
![]() $\mathbf {Psh}(\mathcal {C},\mathrm {Sp}^O_G)$
is called a local weak equivalence if the induced morphism of presheaves
$\mathbf {Psh}(\mathcal {C},\mathrm {Sp}^O_G)$
is called a local weak equivalence if the induced morphism of presheaves
 $$ \begin{align*} &(X\in \mathcal{C} \mapsto \operatorname{\mathrm{Hom}}_{\mathrm{Ho}(\mathbf{Psh}(\mathcal{C},\mathrm{Sp}^O_G))}(\Sigma^n\Sigma^{\infty} (G/H\times X)_+,\mathcal{F}) \\ \to & (X\in \mathcal{C} \mapsto \operatorname{\mathrm{Hom}}_{\mathrm{Ho}(\mathbf{Psh}(\mathcal{C},\mathrm{Sp}^O_G))}(\Sigma^n\Sigma^{\infty} (G/H\times X)_+,\mathcal{G}) \end{align*} $$
$$ \begin{align*} &(X\in \mathcal{C} \mapsto \operatorname{\mathrm{Hom}}_{\mathrm{Ho}(\mathbf{Psh}(\mathcal{C},\mathrm{Sp}^O_G))}(\Sigma^n\Sigma^{\infty} (G/H\times X)_+,\mathcal{F}) \\ \to & (X\in \mathcal{C} \mapsto \operatorname{\mathrm{Hom}}_{\mathrm{Ho}(\mathbf{Psh}(\mathcal{C},\mathrm{Sp}^O_G))}(\Sigma^n\Sigma^{\infty} (G/H\times X)_+,\mathcal{G}) \end{align*} $$
becomes an isomorphism after sheafification for every subgroup H of G and integer n. There is a local projective model structure; see [Reference Ayoub3, Definition 4.4.34]. This is a Bousfield localization of the projective model structure with respect to local weak equivalences.
Proposition 3.3.12. Let
![]() $\mathcal {C}$
be a site. The underlying
$\mathcal {C}$
be a site. The underlying
![]() $\infty $
-category of
$\infty $
-category of
![]() $\mathbf {Psh}(\mathcal {C},\mathrm {Sp}^O_{{\mathbb {Z}/2}})$
with respect to the local projective model structure is equivalent to
$\mathbf {Psh}(\mathcal {C},\mathrm {Sp}^O_{{\mathbb {Z}/2}})$
with respect to the local projective model structure is equivalent to
![]() $\mathcal {S}\mathrm {hv}(\mathcal {C},\mathrm {Sp}_{{\mathbb {Z}/2}})$
.
$\mathcal {S}\mathrm {hv}(\mathcal {C},\mathrm {Sp}_{{\mathbb {Z}/2}})$
.
Proof. Let
![]() $f\colon \mathcal {F}\to \mathcal {G}$
be a morphism of fibrant objects in
$f\colon \mathcal {F}\to \mathcal {G}$
be a morphism of fibrant objects in
![]() $\mathbf {Psh}(\mathcal {C},\mathrm {Sp}^O_G)$
with respect to the projective model structure. We need to show that f is a local weak equivalence if and only if the corresponding map g in
$\mathbf {Psh}(\mathcal {C},\mathrm {Sp}^O_G)$
with respect to the projective model structure. We need to show that f is a local weak equivalence if and only if the corresponding map g in
![]() $\mathcal {P}\mathrm {sh}(\mathcal {C},\mathrm {Sp}_G)$
is a local equivalence.
$\mathcal {P}\mathrm {sh}(\mathcal {C},\mathrm {Sp}_G)$
is a local equivalence.
By adjunction, f is a local weak equivalence if and only if the induced morphism of presheaves
becomes an isomorphism after sheafification for
![]() $H=e,{\mathbb {Z}/2}$
and integer n. By [Reference Dugger, Hollander and Isaksen18, Theorem 1.3], this is equivalent to saying that
$H=e,{\mathbb {Z}/2}$
and integer n. By [Reference Dugger, Hollander and Isaksen18, Theorem 1.3], this is equivalent to saying that
![]() $i^*g$
and
$i^*g$
and
![]() $g^{{\mathbb {Z}/2}}$
are local equivalences. Proposition 3.3.7 finishes the proof.
$g^{{\mathbb {Z}/2}}$
are local equivalences. Proposition 3.3.7 finishes the proof.
Proposition 3.3.13. Let
![]() $\mathcal {C}$
and
$\mathcal {C}$
and
![]() $\mathcal {C}'$
be sites. If there is an equivalence of topoi
$\mathcal {C}'$
be sites. If there is an equivalence of topoi
![]() $\mathbf {Shv}(\mathcal {C})\simeq \mathbf {Shv}(\mathcal {C}')$
, then there is an equivalence of
$\mathbf {Shv}(\mathcal {C})\simeq \mathbf {Shv}(\mathcal {C}')$
, then there is an equivalence of
![]() $\infty $
-categories
$\infty $
-categories
Proof. Apply [Reference Ayoub3, Proposition 4.4.56] to the canonical (compose Yoneda and sheafification) functors
![]() $\mathcal {C}\to \mathbf {Shv}(\mathcal {C})$
and
$\mathcal {C}\to \mathbf {Shv}(\mathcal {C})$
and
![]() $\mathcal {C}'\to \mathbf {Shv}(\mathcal {C}')$
, where the right-hand side categories are equipped with the topology described in [Reference Ayoub3, after Théorème 4.4.51]. Hence, we obtain left Quillen equivalences
$\mathcal {C}'\to \mathbf {Shv}(\mathcal {C}')$
, where the right-hand side categories are equipped with the topology described in [Reference Ayoub3, after Théorème 4.4.51]. Hence, we obtain left Quillen equivalences
with respect to the local model structures of Definition 3.3.11. Owing to Proposition 3.3.12 and [Reference Lurie42, Lemma 1.3.4.21], we obtain equivalences of
![]() $\infty $
-categories
$\infty $
-categories
We obtain the desired equivalence of
![]() $\infty $
-categories thanks to the equivalence of topoi (and hence sites)
$\infty $
-categories thanks to the equivalence of topoi (and hence sites)
![]() $\mathbf {Shv}(\mathcal {C})\simeq \mathbf {Shv}(\mathcal {C}')$
.
$\mathbf {Shv}(\mathcal {C})\simeq \mathbf {Shv}(\mathcal {C}')$
.
3.4 Isovariant étale descent
For an abelian group M, equation (2.7) gives a canonical equivalence
The last adjunction in equation (2.2) then yields a maps
![]() $\iota \mathrm {H} M \to \mathrm {H} \iota M$
. We have a similar map for a commutative ring A.
$\iota \mathrm {H} M \to \mathrm {H} \iota M$
. We have a similar map for a commutative ring A.
Lemma 3.4.1. Let A be a commutative ring and M a flat A-module. Then there is an equivalence
Proof. By Proposition Appendix A.3.6,
![]() $\mathrm {H}$
preserves filtered colimits. The two functors
$\mathrm {H}$
preserves filtered colimits. The two functors
![]() $\iota $
also preserve filtered colimits since they are left adjoints. Every flat A-module is a filtered colimit of finitely generated free A-modules by Lazard’s theorem, so we reduce to the case when M is a finitely generated free A-module. In this case, the claim is clear.
$\iota $
also preserve filtered colimits since they are left adjoints. Every flat A-module is a filtered colimit of finitely generated free A-modules by Lazard’s theorem, so we reduce to the case when M is a finitely generated free A-module. In this case, the claim is clear.
For a scheme X, let
![]() $\mathbf {\acute {E}t}\mathbf {Aff}/X$
denote the category of affine schemes étale over X. We start by considering the affine case
$\mathbf {\acute {E}t}\mathbf {Aff}/X$
denote the category of affine schemes étale over X. We start by considering the affine case
![]() $X=\operatorname {\mathrm {Spec}}(A)$
.
$X=\operatorname {\mathrm {Spec}}(A)$
.
Lemma 3.4.2. Let A be a commutative ring, and let M be an
![]() $\mathrm {H} A$
-module. The presheaf
$\mathrm {H} A$
-module. The presheaf
![]() $\mathcal {F}$
of spectra on
$\mathcal {F}$
of spectra on
![]() $\mathbf {\acute {E}t}\mathbf {Aff}/\operatorname {\mathrm {Spec}}(A)$
given by
$\mathbf {\acute {E}t}\mathbf {Aff}/\operatorname {\mathrm {Spec}}(A)$
given by
for étale homomorphisms
![]() $A\to B$
satisfies étale descent.
$A\to B$
satisfies étale descent.
Proof. Since
![]() $\mathrm {H} A\to \mathrm {H} B$
is flat in the sense of [Reference Lurie42, Definition 7.2.2.10], we have an isomorphism
$\mathrm {H} A\to \mathrm {H} B$
is flat in the sense of [Reference Lurie42, Definition 7.2.2.10], we have an isomorphism
for all integers q. In particular,
![]() $\pi _q \mathcal {F}$
is a quasi-coherent sheaf on
$\pi _q \mathcal {F}$
is a quasi-coherent sheaf on
![]() $\mathbf {\acute {E}t}\mathbf {Aff}/\operatorname {\mathrm {Spec}}(A)$
.
$\mathbf {\acute {E}t}\mathbf {Aff}/\operatorname {\mathrm {Spec}}(A)$
.
According to the paragraph preceding [Reference Geisser and Hesselholt21, Proposition 3.1.2], there is a conditionally convergent spectral sequence
where
![]() $a_{{\acute {e}t}}$
denotes the étale sheafification functor. Since
$a_{{\acute {e}t}}$
denotes the étale sheafification functor. Since
![]() $\pi _{-t}\mathcal {F}$
is a quasi-coherent sheaf for every integer t, the cohomology
$\pi _{-t}\mathcal {F}$
is a quasi-coherent sheaf for every integer t, the cohomology
![]() $H^s(X,a_{{\acute {e}t}} \pi _{-t}\mathcal {F})$
vanishes for every integer
$H^s(X,a_{{\acute {e}t}} \pi _{-t}\mathcal {F})$
vanishes for every integer
![]() $s\neq 0$
. It follows that
$s\neq 0$
. It follows that
![]() $\pi _{-t}\mathcal {F}\to \pi _{-t}L_{{\acute {e}t}}\mathcal {F}$
is an isomorphism for every integer t, that is,
$\pi _{-t}\mathcal {F}\to \pi _{-t}L_{{\acute {e}t}}\mathcal {F}$
is an isomorphism for every integer t, that is,
![]() $\mathcal {F}$
satisfies étale descent.
$\mathcal {F}$
satisfies étale descent.
Let A be a commutative ring with involution. Let
![]() $\mathbf {iso\acute {E}tAff}/\operatorname {\mathrm {Spec}}(A)$
denote the category of affine schemes with involutions isovariant étale over
$\mathbf {iso\acute {E}tAff}/\operatorname {\mathrm {Spec}}(A)$
denote the category of affine schemes with involutions isovariant étale over
![]() $\operatorname {\mathrm {Spec}}(A)$
.
$\operatorname {\mathrm {Spec}}(A)$
.
Theorem 3.4.3. The presheaf
satisfies isovariant étale descent, where
![]() $\mathbf {Aff}_{{\mathbb {Z}/2}}$
denotes the category of affine schemes with involutions.
$\mathbf {Aff}_{{\mathbb {Z}/2}}$
denotes the category of affine schemes with involutions.
Proof. We only need to show that the restriction of
![]() $\mathrm {THR}$
to
$\mathrm {THR}$
to
![]() $\mathbf {iso\acute {E}tAff}/\operatorname {\mathrm {Spec}}(A)$
satisfies isovariant étale descent. The functor
$\mathbf {iso\acute {E}tAff}/\operatorname {\mathrm {Spec}}(A)$
satisfies isovariant étale descent. The functor
sending
![]() $\operatorname {\mathrm {Spec}}(B)$
to
$\operatorname {\mathrm {Spec}}(B)$
to
![]() $\operatorname {\mathrm {Spec}}(A\otimes _{\iota A^{{\mathbb {Z}/2}}}\iota B)$
is an equivalence of sites by Proposition 3.1.4. Let
$\operatorname {\mathrm {Spec}}(A\otimes _{\iota A^{{\mathbb {Z}/2}}}\iota B)$
is an equivalence of sites by Proposition 3.1.4. Let
be the presheaf given by
![]() $ \mathcal {F}(\operatorname {\mathrm {Spec}}(B)) := \mathrm {THR}(A)\wedge _{\mathrm {H} \iota A^{{\mathbb {Z}/2}}}\mathrm {H} \iota B $
for étale homomorphisms
$ \mathcal {F}(\operatorname {\mathrm {Spec}}(B)) := \mathrm {THR}(A)\wedge _{\mathrm {H} \iota A^{{\mathbb {Z}/2}}}\mathrm {H} \iota B $
for étale homomorphisms
![]() $A^{{\mathbb {Z}/2}}\to B$
. If we show that
$A^{{\mathbb {Z}/2}}\to B$
. If we show that
![]() $\mathcal {F}$
satisfies étale descent, then the presheaf
$\mathcal {F}$
satisfies étale descent, then the presheaf
obtained from
![]() $\mathcal {F}$
and errant (3.8) satisfies isovariant étale descent. Theorem 3.2.3 gives the third equivalence in
$\mathcal {F}$
and errant (3.8) satisfies isovariant étale descent. Theorem 3.2.3 gives the third equivalence in
that is,
![]() $\mathcal {G}\simeq \mathrm {THR}$
. This means that
$\mathcal {G}\simeq \mathrm {THR}$
. This means that
![]() $\mathrm {THR}$
satisfies isovariant étale descent.
$\mathrm {THR}$
satisfies isovariant étale descent.
Hence, it remains to check that
![]() $\mathcal {F}$
satisfies étale descent. There is an equivalence
$\mathcal {F}$
satisfies étale descent. There is an equivalence
By Lemmas Appendix A.2.9 and 3.4.1, there are equivalences
Lemma 3.4.2 implies that
![]() $i^*\mathcal {F}$
and
$i^*\mathcal {F}$
and
![]() $\mathcal {F}^{{\mathbb {Z}/2}}$
satisfy étale descent, which means that
$\mathcal {F}^{{\mathbb {Z}/2}}$
satisfy étale descent, which means that
![]() $\mathcal {F}$
satisfies étale descent.
$\mathcal {F}$
satisfies étale descent.
Proposition 3.4.4. For every separated scheme X with involution, there exists an isovariant étale covering
![]() $\{U_i\to X\}_{i\in I}$
such that each
$\{U_i\to X\}_{i\in I}$
such that each
![]() $U_i$
is an affine scheme with involution.
$U_i$
is an affine scheme with involution.
Proof. Let
![]() $X^{{\mathbb {Z}/2}}$
denote the closed subscheme of X obtained by Definition 3.1.5. We set
$X^{{\mathbb {Z}/2}}$
denote the closed subscheme of X obtained by Definition 3.1.5. We set
![]() $Y:=X-X^{{\mathbb {Z}/2}}$
, which is an open subscheme of X.
$Y:=X-X^{{\mathbb {Z}/2}}$
, which is an open subscheme of X.
If x is a point of
![]() $X^{{\mathbb {Z}/2}}$
, choose an affine open neighborhood
$X^{{\mathbb {Z}/2}}$
, choose an affine open neighborhood
![]() $U_x$
of x in X. Then
$U_x$
of x in X. Then
![]() $V_x:=U_x\cap w(U_x)$
is again an affine open neighborhood of x since X is separated, and w can be restricted to
$V_x:=U_x\cap w(U_x)$
is again an affine open neighborhood of x since X is separated, and w can be restricted to
![]() $V_x$
. It follows that
$V_x$
. It follows that
is a Zariski covering.
The
![]() ${\mathbb {Z}/2}$
-action on Y is free, so the quotient morphism
${\mathbb {Z}/2}$
-action on Y is free, so the quotient morphism
![]() $Y\to Y/({\mathbb {Z}/2})$
is étale since the algebraic space
$Y\to Y/({\mathbb {Z}/2})$
is étale since the algebraic space
![]() $Y/({\mathbb {Z}/2})$
is formed by the étale equivalence relation
$Y/({\mathbb {Z}/2})$
is formed by the étale equivalence relation
![]() $Y\times {\mathbb {Z}/2} \rightrightarrows Y$
, and there is an isomorphism
$Y\times {\mathbb {Z}/2} \rightrightarrows Y$
, and there is an isomorphism
![]() $Y\times _{Y/({\mathbb {Z}/2})}Y\cong Y\times {\mathbb {Z}/2}$
. It follows that the morphism
$Y\times _{Y/({\mathbb {Z}/2})}Y\cong Y\times {\mathbb {Z}/2}$
. It follows that the morphism
![]() $Y\times {\mathbb {Z}/2}\to Y$
obtained by the first projection
$Y\times {\mathbb {Z}/2}\to Y$
obtained by the first projection
![]() $Y\times _{Y/({\mathbb {Z}/2})}Y\to Y$
is isovariant étale. Choose a Zariski covering
$Y\times _{Y/({\mathbb {Z}/2})}Y\to Y$
is isovariant étale. Choose a Zariski covering
![]() $\{W_j\to Y\}_{j\in J}$
after forgetting involution such that each
$\{W_j\to Y\}_{j\in J}$
after forgetting involution such that each
![]() $W_j$
is an affine scheme, and then
$W_j$
is an affine scheme, and then
is an isovariant étale covering.
Let
![]() $\mathbf {Sch}_{{\mathbb {Z}/2}}$
denote the category of separated schemes with involutions.
$\mathbf {Sch}_{{\mathbb {Z}/2}}$
denote the category of separated schemes with involutions.
Proposition 3.4.5. There is an equivalence of topoi
Hence, there is an equivalence of
![]() $\infty $
-categories
$\infty $
-categories
Proof. Combine [Reference Artin, Grothendieck and Verdier2, Théorème III.4.1] and Proposition 3.4.4 to obtain equation (3.10). Use Proposition 3.3.13 for equation (3.11).
Definition 3.4.6. By Theorem 3.4.3 and Proposition 3.4.5, we obtain
This definition immediately implies that
![]() $\mathrm {THR}(X)$
that satisfies isovariant étale descent for all
$\mathrm {THR}(X)$
that satisfies isovariant étale descent for all
![]() $X\in \mathbf {Sch}_{{\mathbb {Z}/2}}$
.
$X\in \mathbf {Sch}_{{\mathbb {Z}/2}}$
.
Below, we carry out computations of
![]() $\mathrm {THR}(X)$
for projective spaces
$\mathrm {THR}(X)$
for projective spaces
![]() $X=\mathbb {P}^n$
, even with involution for
$X=\mathbb {P}^n$
, even with involution for
![]() $n=1$
. Let us first check that extending Proposition 2.1.3 to schemes yields a definition of
$n=1$
. Let us first check that extending Proposition 2.1.3 to schemes yields a definition of
![]() ${\mathrm {THH}}$
for schemes equivalent to the one of [Reference Geisser and Hesselholt21] as follows. See, for example, [Reference Blumberg and Mandell10, p. 1055 and chapter 3] for a discussion of other equivalent definitions of
${\mathrm {THH}}$
for schemes equivalent to the one of [Reference Geisser and Hesselholt21] as follows. See, for example, [Reference Blumberg and Mandell10, p. 1055 and chapter 3] for a discussion of other equivalent definitions of
![]() ${\mathrm {THH}}(X)$
.
${\mathrm {THH}}(X)$
.
Proposition 3.4.7. For
![]() $X\in \mathbf {Sch}_{{\mathbb {Z}/2}}$
and
$X\in \mathbf {Sch}_{{\mathbb {Z}/2}}$
and
![]() $Y\in \mathbf {Sch}$
, there are canonical equivalences
$Y\in \mathbf {Sch}$
, there are canonical equivalences
where the involution on
![]() $Y\amalg Y$
switches the components.
$Y\amalg Y$
switches the components.
Proof. The question is isovariant étale local on X and étale local on Y, so we reduce to the case when
![]() $X=\operatorname {\mathrm {Spec}}(A)$
for some commutative ring A with involution and
$X=\operatorname {\mathrm {Spec}}(A)$
for some commutative ring A with involution and
![]() $Y=\operatorname {\mathrm {Spec}}(B)$
for some commutative ring B. We obtain equivalences
$Y=\operatorname {\mathrm {Spec}}(B)$
for some commutative ring B. We obtain equivalences
using Proposition 2.1.3 and equation (2.7). We similarly obtain the remaining desired equivalence using Propositions 2.1.4 and 2.3.3.
Definition 3.4.8. Recall from [Reference Heller, Krishna and Østvær26, section 2.1] that an equivariant Nisnevich distinguished square is a Cartesian square in
![]() $\mathbf {Sch}_{{\mathbb {Z}/2}}$
of the form
$\mathbf {Sch}_{{\mathbb {Z}/2}}$
of the form

such that j is an open immersion, f is equivariant étale and the morphism of schemes
![]() $(Y-V)_{\mathrm {red}}\to (X-U)_{\mathrm {red}}$
is an isomorphism. The collection of such squares forms a cd-structure, which is bounded, complete and regular in the sense of [Reference Voevodsky58] by [Reference Heller, Krishna and Østvær26, Theorem 2.3]. Furthermore, the associated topology is the equivariant Nisnevich topology in Definition 3.1.1 by [Reference Heller, Krishna and Østvær26, Proposition 2.17].
$(Y-V)_{\mathrm {red}}\to (X-U)_{\mathrm {red}}$
is an isomorphism. The collection of such squares forms a cd-structure, which is bounded, complete and regular in the sense of [Reference Voevodsky58] by [Reference Heller, Krishna and Østvær26, Theorem 2.3]. Furthermore, the associated topology is the equivariant Nisnevich topology in Definition 3.1.1 by [Reference Heller, Krishna and Østvær26, Proposition 2.17].
Corollary 3.4.9. For every equivariant Nisnevich distinguished square Q of the form (3.12), the induced square

is Cartesian.
Proof. Let P be the collection of equivariant Nisnevich distinguished squares. Consider the class
![]() $G_P$
of morphisms between simplicial presheaves in [Reference Voevodsky58, p. 1392]. By [Reference Voevodsky58, Proposition 3.8(2)], every
$G_P$
of morphisms between simplicial presheaves in [Reference Voevodsky58, p. 1392]. By [Reference Voevodsky58, Proposition 3.8(2)], every
![]() $G_P$
-local equivalence is an equivariant Nisnevich local equivalence. This implies that if
$G_P$
-local equivalence is an equivariant Nisnevich local equivalence. This implies that if
![]() $\mathcal {F}$
is a simplicial presheaf satisfying equivariant Nisnevich descent, then
$\mathcal {F}$
is a simplicial presheaf satisfying equivariant Nisnevich descent, then
![]() $\mathcal {F}(Q)$
is Cartesian for all
$\mathcal {F}(Q)$
is Cartesian for all
![]() $Q\in P$
.
$Q\in P$
.
Since
![]() $\mathrm {THR}$
satisfies isovariant étale descent, it satisfies equivariant Nisnevich descent. Hence, we can apply the argument in the above paragraph to
$\mathrm {THR}$
satisfies isovariant étale descent, it satisfies equivariant Nisnevich descent. Hence, we can apply the argument in the above paragraph to
![]() $\Omega ^{\infty } \Sigma ^n i^* \mathrm {THR}$
and
$\Omega ^{\infty } \Sigma ^n i^* \mathrm {THR}$
and
![]() $\Omega ^{\infty } \Sigma ^n \Phi ^{{\mathbb {Z}/2}} \mathrm {THR}$
for all integers n to see that
$\Omega ^{\infty } \Sigma ^n \Phi ^{{\mathbb {Z}/2}} \mathrm {THR}$
for all integers n to see that
![]() $i^*\mathrm {THR}(Q)$
and
$i^*\mathrm {THR}(Q)$
and
![]() $\Phi ^{{\mathbb {Z}/2}}\mathrm {THR}(Q)$
are Cartesian, which implies the claim.
$\Phi ^{{\mathbb {Z}/2}}\mathrm {THR}(Q)$
are Cartesian, which implies the claim.
For the computations about
![]() $\mathrm {THR}(\mathbb {P}^n)$
we provide in the next sections, we may simply use appropriate equivariant Nisnevich covers by affine schemes and Corollary 3.4.9, which, for example, exhibits
$\mathrm {THR}(\mathbb {P}^n)$
we provide in the next sections, we may simply use appropriate equivariant Nisnevich covers by affine schemes and Corollary 3.4.9, which, for example, exhibits
![]() $\mathrm {THR}(\mathbb {P}^1)$
as part of a homotopy co-Cartesian square in which all other entries are of the form
$\mathrm {THR}(\mathbb {P}^1)$
as part of a homotopy co-Cartesian square in which all other entries are of the form
![]() $\mathrm {THR}(Y)$
for
$\mathrm {THR}(Y)$
for
![]() $Y=\operatorname {\mathrm {Spec}}(A[M])$
corresponding to some commutative monoid rings for
$Y=\operatorname {\mathrm {Spec}}(A[M])$
corresponding to some commutative monoid rings for
![]() $M=\mathbb {N}$
or
$M=\mathbb {N}$
or
![]() $M=\mathbb {Z}$
over the commutative base ring A. We could even go one step further and define
$M=\mathbb {Z}$
over the commutative base ring A. We could even go one step further and define
![]() $\mathrm {THR}(\mathbb {P}^n_{\mathbb {S}},\sigma )$
for projective spaces, possibly with nontrivial involution
$\mathrm {THR}(\mathbb {P}^n_{\mathbb {S}},\sigma )$
for projective spaces, possibly with nontrivial involution
![]() $\sigma $
, over the sphere spectrum
$\sigma $
, over the sphere spectrum
![]() $\mathbb {S}$
rather than over A or
$\mathbb {S}$
rather than over A or
![]() $\mathrm {H} A$
, using the homotopy pushout of the appropriate diagram of THR of the corresponding spherical monoid rings
$\mathrm {H} A$
, using the homotopy pushout of the appropriate diagram of THR of the corresponding spherical monoid rings
![]() $\mathbb {S}[M]$
, compare the proofs in section 5.1.
$\mathbb {S}[M]$
, compare the proofs in section 5.1.
4 The dihedral bar construction
4.1 Crossed simplicial groups
Hochschild and cyclic homology and their real refinements are closely related to cyclic, real and dihedral nerves. We now present a uniform treatment of these constructions. The original references are [Reference Fiedorowicz and Loday20] and [Reference Loday and Ronco40]; parts of this are also explained, for example, in [Reference Dotto and Ogle17] and [Reference Dotto, Moi, Patchkoria and Reeh16].
Definition 4.1.1. (See [Reference Fiedorowicz and Loday20, Definition 1.1],[Reference Loday and Ronco40, chapter 6.3]) A crossed simplicial group G is a sequence of groups
![]() $\{G_n\}_{n\geq 0}$
together with a category
$\{G_n\}_{n\geq 0}$
together with a category
![]() $\Delta G$
satisfying the following conditions:
$\Delta G$
satisfying the following conditions:
-
(i)
 $\Delta G$
contains
$\Delta G$
contains
 $\Delta $
as a subcategory with the same objects.
$\Delta $
as a subcategory with the same objects. -
(ii)
 $\mathrm {Aut}([n])$
is the opposite group
$\mathrm {Aut}([n])$
is the opposite group
 $G_n^{op}$
.
$G_n^{op}$
. -
(iii) A morphism in
 $\Delta G$
can be uniquely written as the composite
$\Delta G$
can be uniquely written as the composite
 $\alpha \circ g$
for some
$\alpha \circ g$
for some
 $\alpha \in \operatorname {\mathrm {Hom}}_{\Delta }([m],[n])$
and
$\alpha \in \operatorname {\mathrm {Hom}}_{\Delta }([m],[n])$
and
 $g\in G_m^{op}$
.
$g\in G_m^{op}$
.
Observe that every crossed simplicial group is a (or rather has an underlying) simplicial set; see [Reference Fiedorowicz and Loday20, Lemma 1.3]. A G-set is a functor
![]() $\Delta G^{op}\to \mathbf {Set}$
, which by restriction has an underlying simplicial set.
$\Delta G^{op}\to \mathbf {Set}$
, which by restriction has an underlying simplicial set.
Construction 4.1.2. Let X be a simplicial set. For a crossed simplicial group G, the G-set
![]() $F_G(X)$
is defined in [Reference Fiedorowicz and Loday20, Definition 4.3]. In simplicial degree q, we have
$F_G(X)$
is defined in [Reference Fiedorowicz and Loday20, Definition 4.3]. In simplicial degree q, we have
The
![]() $G_q$
action on
$G_q$
action on
![]() $F_G(X)_q$
is the left multiplication on
$F_G(X)_q$
is the left multiplication on
![]() $G_q$
. The faces and degeneracy maps are given by
$G_q$
. The faces and degeneracy maps are given by
According to [Reference Fiedorowicz and Loday20, Proposition 5.1], we have the projection
![]() $p_1\colon F_G(X)\to G$
given by
$p_1\colon F_G(X)\to G$
given by
![]() $p_1(g,x):=g$
. We also have the projection
$p_1(g,x):=g$
. We also have the projection
![]() $p_2\colon \lvert F_G(X)\rvert \to \lvert X \rvert $
given by
$p_2\colon \lvert F_G(X)\rvert \to \lvert X \rvert $
given by
for
![]() $u\in \Delta _{top}^q$
. Furthermore, the two projections define a homeomorphism
$u\in \Delta _{top}^q$
. Furthermore, the two projections define a homeomorphism
If X is a G-set, then we have the evaluation map
![]() $ev\colon F_G(X) \to X$
given by
$ev\colon F_G(X) \to X$
given by
According to [Reference Fiedorowicz and Loday20, Theorem 5.3], the composite map
defines a
![]() $\lvert G \rvert $
-action on
$\lvert G \rvert $
-action on
![]() $\lvert X \rvert $
. The G-geometric realization of X is
$\lvert X \rvert $
. The G-geometric realization of X is
![]() $\lvert X\rvert $
with this
$\lvert X\rvert $
with this
![]() $\lvert G\rvert $
-action.
$\lvert G\rvert $
-action.
Example 4.1.3. We have the following three fundamental examples of crossed simplicial groups.
-
(1) [Reference Fiedorowicz and Loday20, Example 2, section 1.5] introduces a crossed simplicial group G with
 $G_n:={\mathbb {Z}/2}$
. For this G, a G-set is called a real simplicial set. The G-geometric realization is called the real geometric realization.
$G_n:={\mathbb {Z}/2}$
. For this G, a G-set is called a real simplicial set. The G-geometric realization is called the real geometric realization.Explicitly, a real simplicial set X is a simplicial set equipped with isomorphisms
 $w_n\colon X_n\to X_n$
with
$w_n\colon X_n\to X_n$
with
 $w_n^2=\mathrm {id}$
for all integers
$w_n^2=\mathrm {id}$
for all integers
 $n\geq 1$
satisfying the relations for
$n\geq 1$
satisfying the relations for $$\begin{align*}d_i w_n=w_{n-1}d_{n-i} \text{ and } s_i w_n = w_{n+1}s_{n-i} \end{align*}$$
$$\begin{align*}d_i w_n=w_{n-1}d_{n-i} \text{ and } s_i w_n = w_{n+1}s_{n-i} \end{align*}$$
 $0\leq i\leq n$
.
$0\leq i\leq n$
.
-
(2) [Reference Fiedorowicz and Loday20, Example 4, section 1.5] introduces a crossed simplicial group G with
 $G_n:=C_{n+1}$
. For this G, a G-set is called a cyclic set, which was defined by Connes. The G-geometric realization is called the cyclic geometric realization and comes with an action of
$G_n:=C_{n+1}$
. For this G, a G-set is called a cyclic set, which was defined by Connes. The G-geometric realization is called the cyclic geometric realization and comes with an action of
 $S^1=SO(2)$
(see also [Reference Loday and Ronco40, Theorem 7.1.4]).
$S^1=SO(2)$
(see also [Reference Loday and Ronco40, Theorem 7.1.4]).Explicitly, a cyclic set X is a simplicial set equipped with isomorphisms
 $t_n\colon X_n\to X_n$
with
$t_n\colon X_n\to X_n$
with
 $(t_n)^{n+1}=\mathrm {id}$
for all integers
$(t_n)^{n+1}=\mathrm {id}$
for all integers
 $n\geq 1$
satisfying the relations for
$n\geq 1$
satisfying the relations for $$\begin{align*}d_it_n=t_{n-1}d_{i-1} \text{ and } s_it_n=t_{n+1}s_{i-1} \end{align*}$$
$$\begin{align*}d_it_n=t_{n-1}d_{i-1} \text{ and } s_it_n=t_{n+1}s_{i-1} \end{align*}$$
 $1\leq i\leq n$
.
$1\leq i\leq n$
.
-
(3) [Reference Fiedorowicz and Loday20, Example 5, section 1.5] introduces a crossed simplicial group G with
 $G_n:=D_{n+1}$
, where
$G_n:=D_{n+1}$
, where
 $D_n$
denotes the dihedral group of order
$D_n$
denotes the dihedral group of order
 $2n$
. For this G, a G-set is called a dihedral set. The G-geometric realization is called the dihedral geometric realization.
$2n$
. For this G, a G-set is called a dihedral set. The G-geometric realization is called the dihedral geometric realization.
Explicitly, a dihedral set X is a simplicial set equipped with
![]() $t_n$
and
$t_n$
and
![]() $w_n$
for all integers
$w_n$
for all integers
![]() $n\geq 1$
satisfying
$n\geq 1$
satisfying
![]() $w_n t_n=t_n^{-1}w_n$
and all the above conditions for
$w_n t_n=t_n^{-1}w_n$
and all the above conditions for
![]() $t_n$
and
$t_n$
and
![]() $w_n$
.
$w_n$
.
There are obvious forgetful functors from dihedral to real and to cyclic sets.
For
![]() $\lvert G \rvert $
, we obtain
$\lvert G \rvert $
, we obtain
![]() ${\mathbb {Z}/2}$
,
${\mathbb {Z}/2}$
,
![]() $S^1=U(1)=SO(2)$
and
$S^1=U(1)=SO(2)$
and
![]() $O(2)$
in the three examples above.
$O(2)$
in the three examples above.
Example 4.1.4. Let G be the crossed simplicial set in Example 4.1.3(1). For a simplicial set X, the bijection
![]() $G \times X_q = X_q \amalg X_q$
induces a canonical isomorphism of G-sets
$G \times X_q = X_q \amalg X_q$
induces a canonical isomorphism of G-sets
where
![]() $w_n\colon X_n\amalg X_n^{op}\to X_n\amalg X_n^{op}$
is the switching map. If X is a real simplicial set, then the evaluation map
$w_n\colon X_n\amalg X_n^{op}\to X_n\amalg X_n^{op}$
is the switching map. If X is a real simplicial set, then the evaluation map
![]() $ev\colon F_G(X)\to X$
sends
$ev\colon F_G(X)\to X$
sends
![]() $x\in X_n^{op}$
to
$x\in X_n^{op}$
to
![]() $w_n(x)$
. It follows that the
$w_n(x)$
. It follows that the
![]() ${\mathbb {Z}/2}$
-action on
${\mathbb {Z}/2}$
-action on
![]() $\lvert X \rvert $
is given by the composite map
$\lvert X \rvert $
is given by the composite map
where the first map is the canonical identity.
Example 4.1.5. Let G be the crossed simplicial set in Example 4.1.3(2). For every integer
![]() $n\geq 0$
, we set
$n\geq 0$
, we set
This is Connes’ cyclic n-complex. We warn the reader that
![]() $F_G(X)$
for a simplicial set is different from the cyclic bar construction.
$F_G(X)$
for a simplicial set is different from the cyclic bar construction.
4.2 Real and dihedral nerves
We now recall how commutative monoids with involution give rise to real and dihedral simplicial sets, refining nerves and cyclic nerves for commutative monoids without involutions.
Definition 4.2.1. Let M be a commutative monoid with involution
![]() $\sigma $
. The real nerve of M, denoted
$\sigma $
. The real nerve of M, denoted
![]() $\mathrm {N}^{\sigma } M$
, is the real simplicial set whose underlying simplicial set is the nerve of M with
$\mathrm {N}^{\sigma } M$
, is the real simplicial set whose underlying simplicial set is the nerve of M with
![]() $(\mathrm {N}^{\sigma } M)_q:=M^{\times q}$
and w is given by
$(\mathrm {N}^{\sigma } M)_q:=M^{\times q}$
and w is given by
in simplicial degree q. The real bar construction, denoted
![]() $\mathrm {B}^{\sigma } M$
, is the real geometric realization of
$\mathrm {B}^{\sigma } M$
, is the real geometric realization of
![]() $\mathrm {N}^{\sigma } M$
. We refer to [Reference Dotto and Ogle17, Example 2.1.1] for a similar account.
$\mathrm {N}^{\sigma } M$
. We refer to [Reference Dotto and Ogle17, Example 2.1.1] for a similar account.
Definition 4.2.2. Let M be a commutative monoid with involution
![]() $\sigma $
. The dihedral nerve of M, denoted
$\sigma $
. The dihedral nerve of M, denoted
![]() $\mathrm {N}^{\mathrm {di}} M$
, is the dihedral set defined as follows. In simplicial degree q, we have
$\mathrm {N}^{\mathrm {di}} M$
, is the dihedral set defined as follows. In simplicial degree q, we have
![]() $(\mathrm {N}^{\mathrm {di}} M)_q:=M^{\times (q+1)}$
. The face maps are
$(\mathrm {N}^{\mathrm {di}} M)_q:=M^{\times (q+1)}$
. The face maps are
 $$\begin{align*}d_i(x_0,\ldots,x_q) := \left\{ \begin{array}{ll} (x_0,\ldots,x_{i-1},x_i+x_{i+1},x_{i+2},\ldots,x_q) & \text{if }i=0,\ldots,q-1 \\ (x_q+x_0,x_1,\ldots,x_{q-1}) & \text{if }i=q. \end{array} \right.\\[-15pt] \end{align*}$$
$$\begin{align*}d_i(x_0,\ldots,x_q) := \left\{ \begin{array}{ll} (x_0,\ldots,x_{i-1},x_i+x_{i+1},x_{i+2},\ldots,x_q) & \text{if }i=0,\ldots,q-1 \\ (x_q+x_0,x_1,\ldots,x_{q-1}) & \text{if }i=q. \end{array} \right.\\[-15pt] \end{align*}$$
The degeneracy maps are
The rotation maps are
The involution is
compare also with [Reference Dotto and Ogle17, Example 2.1.2].
Remark 4.2.3. This involution looks similar to the involution on the Hochschild complex as studied in [Reference Loday and Ronco40, 5.2.1]. In [Reference Loday and Ronco40, section 5.2] Loday investigates several ‘real’ versions of Hochschild and cyclic homology for rings. The decompositions of [Reference Loday and Ronco40, Proposition 5.2.3, (5.2.7.1)] should be compared to the Bott sequence [Reference Schlichting52, section 6] relating algebraic to Hermitian K-theory, which also splits after inverting
![]() $2$
or rather
$2$
or rather
![]() $1- \epsilon $
.
$1- \epsilon $
.
Note that we obtain the cyclic nerve of M [Reference Waldhausen59, section 2.3], denoted
![]() $\mathrm {N}^{\mathrm {cy}} M$
, if we forget the involution structure.
$\mathrm {N}^{\mathrm {cy}} M$
, if we forget the involution structure.
The dihedral bar construction, denoted
![]() $\mathrm {B}^{\mathrm {di}} M$
, is the dihedral geometric realization of
$\mathrm {B}^{\mathrm {di}} M$
, is the dihedral geometric realization of
![]() $\mathrm {N}^{\mathrm {di}} M$
. By Construction 4.1.2,
$\mathrm {N}^{\mathrm {di}} M$
. By Construction 4.1.2,
![]() $\mathrm {B}^{\mathrm {di}} M$
admits a canonical
$\mathrm {B}^{\mathrm {di}} M$
admits a canonical
![]() $O(2)$
-action. The underlying real simplicial set of
$O(2)$
-action. The underlying real simplicial set of
![]() $\mathrm {N}^{\mathrm {di}} M$
is different from
$\mathrm {N}^{\mathrm {di}} M$
is different from
![]() $\mathrm {N}^{\sigma } M$
.
$\mathrm {N}^{\sigma } M$
.
We have the map of dihedral sets
sending
![]() $(x_0,\ldots ,x_q)$
to
$(x_0,\ldots ,x_q)$
to
![]() $x_0+\cdots +x_q$
in simplicial degree q, where we regard M as the constant dihedral set whose rotation maps are the identities and whose involutions are given by
$x_0+\cdots +x_q$
in simplicial degree q, where we regard M as the constant dihedral set whose rotation maps are the identities and whose involutions are given by
![]() $\sigma $
. For every
$\sigma $
. For every
![]() $\sigma $
-orbit I in M, we set
$\sigma $
-orbit I in M, we set
Let
![]() $\mathrm {B}^{\mathrm {di}}(M;I)$
be its dihedral geometric realization. We have an isomorphism of dihedral sets
$\mathrm {B}^{\mathrm {di}}(M;I)$
be its dihedral geometric realization. We have an isomorphism of dihedral sets
where the coproduct runs over the
![]() $\sigma $
-orbits in M.
$\sigma $
-orbits in M.
Proposition 4.2.4. Let M and L be commutative monoids with involutions. Then there is an isomorphism of dihedral sets
Proof. The two projections
![]() $M\times L\rightrightarrows M,L$
induce equation (4.5). To show that it is an isomorphism, observe that it is given by the shuffle homomorphism
$M\times L\rightrightarrows M,L$
induce equation (4.5). To show that it is an isomorphism, observe that it is given by the shuffle homomorphism
in simplicial degree q.
Proposition 4.2.5. Let M and L be commutative monoids with the involutions. Then there is an isomorphism of dihedral sets
for all
![]() $x\in M$
and
$x\in M$
and
![]() $y\in L$
.
$y\in L$
.
Proof. This follows from the commutativity of the square

where the upper horizontal homomorphism is the shuffle homomorphism, and the vertical homomorphisms are the summation homomorphisms.
Proposition 4.2.6. Let G be an abelian group with an involution w, and let j be an element of G. If
![]() $j=w(j)$
, then there is an isomorphism of real simplicial sets
$j=w(j)$
, then there is an isomorphism of real simplicial sets
If
![]() $j\neq w(j)$
, then there is an isomorphism of real simplicial sets
$j\neq w(j)$
, then there is an isomorphism of real simplicial sets
As a consequence, there is an isomorphism of real simplicial sets
Proof. If
![]() $j=w(j)$
, the assignment
$j=w(j)$
, the assignment
in simplicial degree q constructs the isomorphism (4.6). If
![]() $j\neq w(j)$
, the assignment
$j\neq w(j)$
, the assignment
in simplicial degree q constructs the isomorphism (4.7), where
![]() $a:=0$
(resp.
$a:=0$
(resp.
![]() $a:=1$
) if
$a:=1$
) if
![]() $x_0+\cdots +x_q=j$
(resp.
$x_0+\cdots +x_q=j$
(resp.
![]() $x_0+\cdots +x_q=-j$
).
$x_0+\cdots +x_q=-j$
).
Definition 4.2.7. Let
![]() $S^{\sigma }$
be the
$S^{\sigma }$
be the
![]() ${\mathbb {Z}/2}$
-space whose underlying space is
${\mathbb {Z}/2}$
-space whose underlying space is
![]() $S^1$
and whose
$S^1$
and whose
![]() ${\mathbb {Z}/2}$
-action is given by the reflection
${\mathbb {Z}/2}$
-action is given by the reflection
![]() $(x,y)\in S^1\subset \mathbb {R}^2\mapsto (x,-y)$
. This is the real geometric realization of the real simplicial set whose underlying simplicial set is the simplicial circle
$(x,y)\in S^1\subset \mathbb {R}^2\mapsto (x,-y)$
. This is the real geometric realization of the real simplicial set whose underlying simplicial set is the simplicial circle
![]() $\Delta ^1/\partial \Delta ^1$
and whose involution on the nondegenerate simplices is the identity. One easily checks that the relations in Example 4.1.3(1) uniquely determines the higher
$\Delta ^1/\partial \Delta ^1$
and whose involution on the nondegenerate simplices is the identity. One easily checks that the relations in Example 4.1.3(1) uniquely determines the higher
![]() $w_n$
. To understand the involution on the real realization, the reader is advised to look at the explanations in Example 4.1.4.
$w_n$
. To understand the involution on the real realization, the reader is advised to look at the explanations in Example 4.1.4.
Proposition 4.2.8. For the additive monoid
![]() $\mathbb {Z}$
with the trivial involution, there is a
$\mathbb {Z}$
with the trivial involution, there is a
![]() ${\mathbb {Z}/2}$
-homotopy equivalence
${\mathbb {Z}/2}$
-homotopy equivalence
Proof. Consider the element
![]() $1\in (\mathrm {N}^{\sigma } \mathbb {Z})_1\simeq \mathbb {Z}$
in simplicial degree
$1\in (\mathrm {N}^{\sigma } \mathbb {Z})_1\simeq \mathbb {Z}$
in simplicial degree
![]() $1$
. This is fixed by the involution on
$1$
. This is fixed by the involution on
![]() $\mathrm {N}^{\sigma } \mathbb {Z}$
, so the real geometric realization of the real simplicial subset of
$\mathrm {N}^{\sigma } \mathbb {Z}$
, so the real geometric realization of the real simplicial subset of
![]() $\mathrm {N}^{\sigma } \mathbb {Z}$
whose only nondegenerate simplices are
$\mathrm {N}^{\sigma } \mathbb {Z}$
whose only nondegenerate simplices are
![]() $1$
and the base point is
$1$
and the base point is
![]() $S^{\sigma }$
. Hence, we obtain a map of
$S^{\sigma }$
. Hence, we obtain a map of
![]() ${\mathbb {Z}/2}$
-spaces
${\mathbb {Z}/2}$
-spaces
![]() $S^{\sigma }\to \mathrm {B}^{\sigma } \mathbb {Z}$
. This is the usual homotopy equivalence after forgetting the involutions. It remains to check that the induced map
$S^{\sigma }\to \mathrm {B}^{\sigma } \mathbb {Z}$
. This is the usual homotopy equivalence after forgetting the involutions. It remains to check that the induced map
is a homotopy equivalence as well.
By [Reference Dotto and Ogle17, Proposition 2.1.6],
![]() $(\mathrm {B}^{\sigma } \mathbb {Z})^{\mathbb {Z}/2}$
is the classifying space of the category
$(\mathrm {B}^{\sigma } \mathbb {Z})^{\mathbb {Z}/2}$
is the classifying space of the category
![]() $\mathop {\mathrm {Sym}}\mathbb {Z}$
, whose objects are integers and whose morphisms are given by
$\mathop {\mathrm {Sym}}\mathbb {Z}$
, whose objects are integers and whose morphisms are given by
 $$\begin{align*}\operatorname{\mathrm{Hom}}_{\mathop{\mathrm{Sym}}\mathbb{Z}}(a,b) := \left\{ \begin{array}{ll} * & \text{if }2\mid a-b, \\ \emptyset & \text{if }2 \nmid a-b. \end{array} \right. \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Hom}}_{\mathop{\mathrm{Sym}}\mathbb{Z}}(a,b) := \left\{ \begin{array}{ll} * & \text{if }2\mid a-b, \\ \emptyset & \text{if }2 \nmid a-b. \end{array} \right. \end{align*}$$
The classifying space of
![]() $\mathop {\mathrm {Sym}}\mathbb {Z}$
is obviously homotopy equivalent to
$\mathop {\mathrm {Sym}}\mathbb {Z}$
is obviously homotopy equivalent to
![]() $S^0$
, and hence we deduce a homotopy equivalence
$S^0$
, and hence we deduce a homotopy equivalence
This implies that
![]() $\pi _n((\mathrm {B}^{\sigma } \mathbb {Z})^{\mathbb {Z}/2})$
is trivial for every integer
$\pi _n((\mathrm {B}^{\sigma } \mathbb {Z})^{\mathbb {Z}/2})$
is trivial for every integer
![]() $n>0$
and
$n>0$
and
![]() $\pi _0((\mathrm {B}^{\sigma } \mathbb {Z})^{\mathbb {Z}/2})$
consists of two points.
$\pi _0((\mathrm {B}^{\sigma } \mathbb {Z})^{\mathbb {Z}/2})$
consists of two points.
Hence, it suffices to show that the map
induced by equation (4.9) is injective. Let
![]() $\mathrm {sd}_{\sigma }$
denote Segal’s edgewise subdivision functor in [Reference Segal54]. In simplicial degree
$\mathrm {sd}_{\sigma }$
denote Segal’s edgewise subdivision functor in [Reference Segal54]. In simplicial degree
![]() $1$
, the two degeneracy maps in
$1$
, the two degeneracy maps in
![]() $\mathrm {sd}_{\sigma }(\mathrm {N}^{\sigma } \mathbb {Z})$
are given by
$\mathrm {sd}_{\sigma }(\mathrm {N}^{\sigma } \mathbb {Z})$
are given by
Then edges
![]() $(x_1,x_2,x_1)$
in the
$(x_1,x_2,x_1)$
in the
![]() ${\mathbb {Z}/2}$
-fixed point space connects
${\mathbb {Z}/2}$
-fixed point space connects
![]() $x_2$
and
$x_2$
and
![]() $2x_1+x_2$
. In simplicial degree
$2x_1+x_2$
. In simplicial degree
![]() $0$
,
$0$
,
![]() $\mathrm {sd}_{\sigma }(S^{\sigma })$
consists of two vertices
$\mathrm {sd}_{\sigma }(S^{\sigma })$
consists of two vertices
![]() $0$
and
$0$
and
![]() $1$
, whose images in
$1$
, whose images in
![]() $\mathrm {B}^{\sigma } \mathbb {Z}$
are not connected. Hence, equation (4.11) is injective as claimed.
$\mathrm {B}^{\sigma } \mathbb {Z}$
are not connected. Hence, equation (4.11) is injective as claimed.
Together with equation (4.6), we obtain an equivalence
for all
![]() $j\in \mathbb {Z}$
.
$j\in \mathbb {Z}$
.
Definition 4.2.9. Let
![]() $\mathbb {Z}^{\sigma }$
denote the monoid
$\mathbb {Z}^{\sigma }$
denote the monoid
![]() $\mathbb {Z}$
with the involution
$\mathbb {Z}$
with the involution
![]() $x\mapsto -x$
for
$x\mapsto -x$
for
![]() $x\in \mathbb {Z}$
.
$x\in \mathbb {Z}$
.
Proposition 4.2.10. There is a
![]() ${\mathbb {Z}/2}$
-homotopy equivalence
${\mathbb {Z}/2}$
-homotopy equivalence
Proof. See [Reference Dotto, Moi, Patchkoria and Reeh16, Example 5.13].
Combine this with equation (4.8) to obtain a
![]() $\mathbb {Z}/2$
-homotopy equivalence
$\mathbb {Z}/2$
-homotopy equivalence
Together with the description of
![]() $i_*$
in equation (A.15), we obtain an equivalence in
$i_*$
in equation (A.15), we obtain an equivalence in
![]() $\mathrm {Sp}_{{\mathbb {Z}/2}}$
$\mathrm {Sp}_{{\mathbb {Z}/2}}$
For every integer j, let
![]() $S^{\sigma }(j)$
denote the space
$S^{\sigma }(j)$
denote the space
![]() $S^1$
with the
$S^1$
with the
![]() $O(2)$
-action, whose
$O(2)$
-action, whose
![]() $SO(2)$
-action is given by
$SO(2)$
-action is given by
![]() $(t,x)\mapsto t^j x$
for
$(t,x)\mapsto t^j x$
for
![]() $t\in SO(2)$
and
$t\in SO(2)$
and
![]() $x\in S^1$
, and whose
$x\in S^1$
, and whose
![]() ${\mathbb {Z}/2}$
-action is given by the complex conjugate
${\mathbb {Z}/2}$
-action is given by the complex conjugate
![]() $x\mapsto \overline {x}$
. Here, we regard
$x\mapsto \overline {x}$
. Here, we regard
![]() $S^1$
as the unit circle in
$S^1$
as the unit circle in
![]() $\mathbb {C}$
. For
$\mathbb {C}$
. For
![]() $j\geq 0$
, let
$j\geq 0$
, let
![]() $\Delta ^j_{\sigma }$
be the
$\Delta ^j_{\sigma }$
be the
![]() ${\mathbb {Z}/2}$
-space whose involution is the reflection mapping the vertex i to
${\mathbb {Z}/2}$
-space whose involution is the reflection mapping the vertex i to
![]() $j-i$
for all
$j-i$
for all
![]() $0\leq i\leq j$
.
$0\leq i\leq j$
.
The following computations refine [Reference Rognes49, Proposition 3.21].
Proposition 4.2.11. We have
![]() $\mathrm {B}^{\mathrm {di}}(\mathbb {N};0)\cong *$
. For every integer
$\mathrm {B}^{\mathrm {di}}(\mathbb {N};0)\cong *$
. For every integer
![]() $j\geq 1$
, there is an
$j\geq 1$
, there is an
![]() $O(2)$
-equivariant homeomorphism
$O(2)$
-equivariant homeomorphism
where the
![]() $C_j$
-action on
$C_j$
-action on
![]() $\Delta ^{j-1}_{\sigma }$
is the cyclic permutation. Hence, there is an
$\Delta ^{j-1}_{\sigma }$
is the cyclic permutation. Hence, there is an
![]() $O(2)$
-equivariant deformation retract
$O(2)$
-equivariant deformation retract
Proof. The
![]() $(j-1)$
-simplex
$(j-1)$
-simplex
![]() $(1,\ldots ,1)$
generates
$(1,\ldots ,1)$
generates
![]() $\mathrm {N}^{\mathrm {cy}}(\mathbb {N};j)$
as a cyclic set. Use this to construct a surjective map of cyclic sets
$\mathrm {N}^{\mathrm {cy}}(\mathbb {N};j)$
as a cyclic set. Use this to construct a surjective map of cyclic sets
In simplicial degree q, this can be written as the map
sending
![]() $(t,f)$
to
$(t,f)$
to
In this formulation, the values are calculated modulo j. Let
![]() $\Lambda _{\sigma }^{j-1}$
be the dihedral set whose underlying cyclic set is
$\Lambda _{\sigma }^{j-1}$
be the dihedral set whose underlying cyclic set is
![]() $\Lambda ^{j-1}$
and whose involution is given by
$\Lambda ^{j-1}$
and whose involution is given by
where
![]() $\rho \colon [j-1]\to [j-1]$
is the map sending
$\rho \colon [j-1]\to [j-1]$
is the map sending
![]() $x\in [j-1]$
to
$x\in [j-1]$
to
![]() $j-1-x$
. Then equation (4.16) becomes a morphism of dihedral sets
$j-1-x$
. Then equation (4.16) becomes a morphism of dihedral sets
The cyclic geometric realization of equation (4.16) is
![]() $S^1$
-homeomorphic to the quotient map
$S^1$
-homeomorphic to the quotient map
see the proof of [Reference Hesselholt28, Lemma 2.2.3] or [Reference Rognes49, Proposition 3.20]. Use the observation in Example 4.1.4 to show that the real geometric realization of
![]() $\lvert \Lambda _{\sigma }^{j-1}\rvert $
is
$\lvert \Lambda _{\sigma }^{j-1}\rvert $
is
![]() ${\mathbb {Z}/2}$
-homeomorphic to
${\mathbb {Z}/2}$
-homeomorphic to
![]() $S^{\sigma } \times \Delta ^{j-1}_{\sigma }$
. Combine these two facts to deduce that the dihedral geometric realization of equation (4.17) is
$S^{\sigma } \times \Delta ^{j-1}_{\sigma }$
. Combine these two facts to deduce that the dihedral geometric realization of equation (4.17) is
![]() $O(2)$
-homeomorphic to the quotient map
$O(2)$
-homeomorphic to the quotient map
In particular, we obtain equation (4.14). Since
![]() $\Delta _{\sigma }^{j-1}$
is
$\Delta _{\sigma }^{j-1}$
is
![]() $D_{j}$
-contractible to its barycenter, we obtain equation (4.15).
$D_{j}$
-contractible to its barycenter, we obtain equation (4.15).
Let us review what the proof of [Reference Rognes49, Proposition 3.21] contains. For every integer
![]() $r\geq 1$
, let
$r\geq 1$
, let
![]() $\mathrm {sd}_r$
denote the r-fold edgewise subdivision functor in [Reference Bökstedt, Hsiang and Madsen11]. For every integer j, the r-fold power map
$\mathrm {sd}_r$
denote the r-fold edgewise subdivision functor in [Reference Bökstedt, Hsiang and Madsen11]. For every integer j, the r-fold power map
![]() $\mathrm {N}^{\mathrm {di}}(\mathbb {Z};j) \to \mathrm {sd}_r\mathrm {N}^{\mathrm {di}}(\mathbb {Z};j)$
given by
$\mathrm {N}^{\mathrm {di}}(\mathbb {Z};j) \to \mathrm {sd}_r\mathrm {N}^{\mathrm {di}}(\mathbb {Z};j)$
given by
induces a homeomorphism
If
![]() $r \nmid j$
, then we have
$r \nmid j$
, then we have
Suppose
![]() $j\geq 0$
. We similarly have a homeomorphism
$j\geq 0$
. We similarly have a homeomorphism
If
![]() $r \nmid j$
, then we have
$r \nmid j$
, then we have
If H is a closed subgroup of
![]() $SO(2)$
, then the induced map
$SO(2)$
, then the induced map
is a homotopy equivalence.
Proposition 4.2.12. For every integer
![]() $j\geq 1$
, the induced map
$j\geq 1$
, the induced map
is an
![]() $O(2)$
-equivariant homotopy equivalence.
$O(2)$
-equivariant homotopy equivalence.
Proof. We need to show that equation (4.23) is a homotopy equivalence for all closed subgroups H of
![]() $O(2)$
.
$O(2)$
.
If
![]() $H=O(2)$
, then
$H=O(2)$
, then
![]() $\mathrm {B}^{\mathrm {di}}(\mathbb {N};j)^{O(2)}=\mathrm {B}^{\mathrm {di}}(\mathbb {Z};j)^{O(2)}=\emptyset $
by equations (4.20) and (4.22). Hence, the remaining case is
$\mathrm {B}^{\mathrm {di}}(\mathbb {N};j)^{O(2)}=\mathrm {B}^{\mathrm {di}}(\mathbb {Z};j)^{O(2)}=\emptyset $
by equations (4.20) and (4.22). Hence, the remaining case is
![]() $H=D_r$
for every integer
$H=D_r$
for every integer
![]() $r\geq 1$
. Since equation (4.18) commutes with w, equation (4.21) is
$r\geq 1$
. Since equation (4.18) commutes with w, equation (4.21) is
![]() ${\mathbb {Z}/2}$
-equivariant. Similarly, equation (4.19) is
${\mathbb {Z}/2}$
-equivariant. Similarly, equation (4.19) is
![]() ${\mathbb {Z}/2}$
-equivariant. Hence, we have the induced homeomorphisms
${\mathbb {Z}/2}$
-equivariant. Hence, we have the induced homeomorphisms
Combine with equation (4.22) to reduce to the case when
![]() $H={\mathbb {Z}/2}$
.
$H={\mathbb {Z}/2}$
.
Propositions 4.2.6 and 4.2.8 give a homotopy equivalence
By Proposition 4.2.11, we also have a homotopy equivalence
![]() $\mathrm {B}^{\mathrm {di}}(\mathbb {N};j)^{{\mathbb {Z}/2}}\simeq S^0$
. Hence, it remains to check that the induced map
$\mathrm {B}^{\mathrm {di}}(\mathbb {N};j)^{{\mathbb {Z}/2}}\simeq S^0$
. Hence, it remains to check that the induced map
is a bijection. Recall that
![]() $\mathrm {sd}_{\sigma }$
denotes Segal’s edgewise subdivision functor. In simplicial degree
$\mathrm {sd}_{\sigma }$
denotes Segal’s edgewise subdivision functor. In simplicial degree
![]() $1$
, the two degeneracy maps in
$1$
, the two degeneracy maps in
![]() $\mathrm {sd}_{\sigma }(\mathrm {N}^{\mathrm {di}}(\mathbb {N};j))$
and
$\mathrm {sd}_{\sigma }(\mathrm {N}^{\mathrm {di}}(\mathbb {N};j))$
and
![]() $\mathrm {sd}_{\sigma }(\mathrm {N}^{\mathrm {di}}(\mathbb {Z};j))$
are given by
$\mathrm {sd}_{\sigma }(\mathrm {N}^{\mathrm {di}}(\mathbb {Z};j))$
are given by
The edge
![]() $(x_0,x_1,x_2,x_1)$
in the
$(x_0,x_1,x_2,x_1)$
in the
![]() ${\mathbb {Z}/2}$
-fixed point spaces connects
${\mathbb {Z}/2}$
-fixed point spaces connects
![]() $(x_0,2x_1+x_2)$
and
$(x_0,2x_1+x_2)$
and
![]() $(x_0+2x_1,x_2)$
. Hence, we have
$(x_0+2x_1,x_2)$
. Hence, we have
and
where
![]() $(x_0,x_1)\sim (x_0',x_1')$
if and only if
$(x_0,x_1)\sim (x_0',x_1')$
if and only if
![]() $x_0-x_0'$
is even. This shows that equation (4.25) is a bijection.
$x_0-x_0'$
is even. This shows that equation (4.25) is a bijection.
Proposition 4.2.13. For a commutative monoid M with involution, there is an equivalence in
![]() $\mathrm {Sp}_{{\mathbb {Z}/2}}$
$\mathrm {Sp}_{{\mathbb {Z}/2}}$
Proof. See [Reference Høgenhaven35], and also [Reference Dotto, Moi, Patchkoria and Reeh16, Proposition 5.9].
Proposition 4.2.14. Let A be a commutative ring with involution, and let M be a commutative monoid with involution. Then there is an equivalence in
![]() $\mathrm {Sp}_{{\mathbb {Z}/2}}$
$\mathrm {Sp}_{{\mathbb {Z}/2}}$
Proof. If we regard M as a
![]() ${\mathbb {Z}/2}$
-set, then M is a coproduct of copies
${\mathbb {Z}/2}$
-set, then M is a coproduct of copies
![]() ${\mathbb {Z}/2}$
and e. If
${\mathbb {Z}/2}$
and e. If
![]() $M=e$
, then the claim is clear. Hence, it suffices to show that there is an equivalence
$M=e$
, then the claim is clear. Hence, it suffices to show that there is an equivalence
where
![]() $(i^* A)^{\oplus {\mathbb {Z}/2}}$
is the commutative monoid
$(i^* A)^{\oplus {\mathbb {Z}/2}}$
is the commutative monoid
![]() $A\oplus A$
with the involution given by
$A\oplus A$
with the involution given by
![]() $(x,y)\mapsto (y,x)$
. By equation (2.7) and Propositions Appendix A.1.10, Appendix A.2.7(3) and 2.3.3, we obtain equivalences
$(x,y)\mapsto (y,x)$
. By equation (2.7) and Propositions Appendix A.1.10, Appendix A.2.7(3) and 2.3.3, we obtain equivalences
Together with the equivalence
![]() $i_{\sharp } i^* \mathbb {S}\simeq \Sigma ^{\infty } ({\mathbb {Z}/2})_+$
, we obtain equation (4.26).
$i_{\sharp } i^* \mathbb {S}\simeq \Sigma ^{\infty } ({\mathbb {Z}/2})_+$
, we obtain equation (4.26).
Proposition 4.2.15. Let A be a commutative ring with involution, and let M be a commutative monoid with involution. Then there is a canonical equivalence in
![]() $\mathrm {Sp}_{{\mathbb {Z}/2}}$
$\mathrm {Sp}_{{\mathbb {Z}/2}}$
Proof. By Propositions 2.1.5 and 4.2.13, we have equivalences
Proposition 4.2.14 finishes the proof.
5 Properties of real topological Hochschild homology
5.1 THR of the projective line
We now establish the first computations of
![]() $\mathrm {THR}$
for nonaffine schemes, namely
$\mathrm {THR}$
for nonaffine schemes, namely
![]() $\mathbb {P}^1$
and
$\mathbb {P}^1$
and
![]() $\mathbb {P}^{\sigma }$
.
$\mathbb {P}^{\sigma }$
.
Remark 5.1.1. Hermitian K-theory
![]() $\mathbf {KO}$
resp.
$\mathbf {KO}$
resp.
![]() $\mathbf {KR}$
is not an orientable theory, that is the usual projective bundle formula as for Chow groups and algebraic K-theory does not hold. The computation of
$\mathbf {KR}$
is not an orientable theory, that is the usual projective bundle formula as for Chow groups and algebraic K-theory does not hold. The computation of
![]() $\mathbb {P}^1$
over regular rings is [Reference Hornbostel31, Proposition 6.1], where a
$\mathbb {P}^1$
over regular rings is [Reference Hornbostel31, Proposition 6.1], where a
![]() $(8,4)$
-motivic periodic spectrum
$(8,4)$
-motivic periodic spectrum
![]() $\mathbf {KO}$
is constructed. This computation is extended by [Reference Schlichting52, Theorem 9.10] to rather general base schemes (still with 2 invertible). For the projective line with involution, a variation of Schlichting’s proof leads to the computation of
$\mathbf {KO}$
is constructed. This computation is extended by [Reference Schlichting52, Theorem 9.10] to rather general base schemes (still with 2 invertible). For the projective line with involution, a variation of Schlichting’s proof leads to the computation of
![]() $\mathbf {KR}(\mathbb {P}^{\sigma })$
, see [Reference Carmody12, Theorem 5.1] and compare [Reference Xie61, Theorem 7.1] and [Reference Hu, Kriz and Ormsby34] for different proofs. In particular, this leads to an equivariant motivic spectrum
$\mathbf {KR}(\mathbb {P}^{\sigma })$
, see [Reference Carmody12, Theorem 5.1] and compare [Reference Xie61, Theorem 7.1] and [Reference Hu, Kriz and Ormsby34] for different proofs. In particular, this leads to an equivariant motivic spectrum
![]() $\mathbf {KR}$
which is
$\mathbf {KR}$
which is
![]() $\mathbb {P}^1 \wedge \mathbb {P}^{\sigma }$
-periodic. For further periodicities of
$\mathbb {P}^1 \wedge \mathbb {P}^{\sigma }$
-periodic. For further periodicities of
![]() $\mathbf {KR}$
, see [Reference Hu, Kriz and Ormsby34, Theorem 10]. In their notation, we have
$\mathbf {KR}$
, see [Reference Hu, Kriz and Ormsby34, Theorem 10]. In their notation, we have
![]() $\mathbb {P}^1 \simeq S^1 \wedge S^{\alpha }$
and
$\mathbb {P}^1 \simeq S^1 \wedge S^{\alpha }$
and
![]() $\mathbb {P}^{\sigma } \simeq S^{\gamma } \wedge S^{\gamma \alpha } \simeq \mathbb {P}^1_{-}$
. For the definition of
$\mathbb {P}^{\sigma } \simeq S^{\gamma } \wedge S^{\gamma \alpha } \simeq \mathbb {P}^1_{-}$
. For the definition of
![]() $S^{\gamma }=S^{\sigma }$
in the motivic setting and a proof of the last equivalence, we refer to [Reference Carmody12, section 2.5]. Although
$S^{\gamma }=S^{\sigma }$
in the motivic setting and a proof of the last equivalence, we refer to [Reference Carmody12, section 2.5]. Although
![]() $\mathrm {THR}$
is not
$\mathrm {THR}$
is not
![]() $\mathbb {A}^1$
-invariant, it seems reasonable to expect that the formulas for
$\mathbb {A}^1$
-invariant, it seems reasonable to expect that the formulas for
![]() $\mathrm {THR}(\mathbb {P}^n)$
are similar to those for
$\mathrm {THR}(\mathbb {P}^n)$
are similar to those for
![]() $\mathbf {KR}$
. In the cases considered below this is indeed the case: The following Proposition implies that
$\mathbf {KR}$
. In the cases considered below this is indeed the case: The following Proposition implies that
![]() $\Omega ^{1 + \alpha }\mathrm {THR} \simeq \Sigma ^{\gamma -1}\mathrm {THR}$
. Smashing with
$\Omega ^{1 + \alpha }\mathrm {THR} \simeq \Sigma ^{\gamma -1}\mathrm {THR}$
. Smashing with
![]() $S^1$
, we obtain the same periodicity as (35) in [Reference Hu, Kriz and Ormsby34]. Similarly, the next proposition corresponds to (36) of loc. cit.
$S^1$
, we obtain the same periodicity as (35) in [Reference Hu, Kriz and Ormsby34]. Similarly, the next proposition corresponds to (36) of loc. cit.
The following computations rely on Proposition 4.2.13 and the computations for dihedral nerves in the previous section.
Theorem 5.1.2. For any
![]() $X \in \mathbf {Sch}_{{\mathbb {Z}/2}}$
, there is an equivalence of
$X \in \mathbf {Sch}_{{\mathbb {Z}/2}}$
, there is an equivalence of
![]() ${\mathbb {Z}/2}$
-spectra
${\mathbb {Z}/2}$
-spectra
Proof. For notational convenience, we will write the proof as if everything takes place over
![]() $\mathbb {S}$
rather than X. Using the description of
$\mathbb {S}$
rather than X. Using the description of
![]() $\mathrm {THR}$
for spherical groups rings from Proposition 4.2.13 and its extension to log schemes with involution from Proposition 4.2.15, we are reduced to consider the following homotopy co-Cartesian square, corresponding to the standard Zariski cover of
$\mathrm {THR}$
for spherical groups rings from Proposition 4.2.13 and its extension to log schemes with involution from Proposition 4.2.15, we are reduced to consider the following homotopy co-Cartesian square, corresponding to the standard Zariski cover of
![]() $\mathbb {P}^1$
by two copies of
$\mathbb {P}^1$
by two copies of
![]() $\mathbb {A}^1$
and using Corollary 3.4.9 and the description of
$\mathbb {A}^1$
and using Corollary 3.4.9 and the description of
![]() $\mathrm {THR}(\mathbb {S}[M])$
from Proposition 4.2.13:
$\mathrm {THR}(\mathbb {S}[M])$
from Proposition 4.2.13:

Here, the notation
![]() $\mathbb {N}$
and
$\mathbb {N}$
and
![]() $-\mathbb {N}$
indicates the two different embeddings of
$-\mathbb {N}$
indicates the two different embeddings of
![]() $\mathbb {A}^1$
in
$\mathbb {A}^1$
in
![]() $\mathbb {P}^1$
. It is crucial to notice that even as
$\mathbb {P}^1$
. It is crucial to notice that even as
![]() $\mathbb {G}_m$
has trivial involution, the involution given by the dihedral nerve (see Definition 4.2.2 above) yields nontrivial involutions. Using the decomposition of equation (4.4) and Propositions 4.2.6, 4.2.8 and 4.2.11, we obtain the following
$\mathbb {G}_m$
has trivial involution, the involution given by the dihedral nerve (see Definition 4.2.2 above) yields nontrivial involutions. Using the decomposition of equation (4.4) and Propositions 4.2.6, 4.2.8 and 4.2.11, we obtain the following
![]() ${\mathbb {Z}/2}$
-equivariant (homotopy) co-Cartesian square:
${\mathbb {Z}/2}$
-equivariant (homotopy) co-Cartesian square:

An obvious cancellation, using Proposition 4.2.12 on the relevant maps, yields the following
![]() ${\mathbb {Z}/2}$
-equivariant (homotopy) co-Cartesian square
${\mathbb {Z}/2}$
-equivariant (homotopy) co-Cartesian square

and the result follows.
We now turn to the slightly more subtle computation of the projective line
![]() $\mathbb {P}^{\sigma }$
with involution. Recall that
$\mathbb {P}^{\sigma }$
with involution. Recall that
![]() $(i_{\sharp },i^*,i_*)$
denotes the free-forgetful-cofree adjunction for the map
$(i_{\sharp },i^*,i_*)$
denotes the free-forgetful-cofree adjunction for the map
![]() $i\colon \mathrm {pt} \to \mathrm {B}({\mathbb {Z}/2})$
. Let
$i\colon \mathrm {pt} \to \mathrm {B}({\mathbb {Z}/2})$
. Let
![]() $\Sigma ^{\sigma }\colon \mathrm {Sp}_{{\mathbb {Z}/2}}\to \mathrm {Sp}_{{\mathbb {Z}/2}}$
be the functor
$\Sigma ^{\sigma }\colon \mathrm {Sp}_{{\mathbb {Z}/2}}\to \mathrm {Sp}_{{\mathbb {Z}/2}}$
be the functor
![]() $\Sigma ^{\infty } S^{\sigma } \wedge (-)$
, which has an inverse functor
$\Sigma ^{\infty } S^{\sigma } \wedge (-)$
, which has an inverse functor
![]() $\Sigma ^{-\sigma }$
since the sphere
$\Sigma ^{-\sigma }$
since the sphere
![]() $\Sigma ^{\infty } S^{\sigma }$
is
$\Sigma ^{\infty } S^{\sigma }$
is
![]() $\wedge $
-invertible in
$\wedge $
-invertible in
![]() $\mathrm {Sp}_{{\mathbb {Z}/2}}$
. For integers m and n, we set
$\mathrm {Sp}_{{\mathbb {Z}/2}}$
. For integers m and n, we set
![]() $\Sigma ^{m+n\sigma }:=\Sigma ^m (\Sigma ^{\sigma })^{\wedge n}$
, which is a functor
$\Sigma ^{m+n\sigma }:=\Sigma ^m (\Sigma ^{\sigma })^{\wedge n}$
, which is a functor
![]() $\mathrm {Sp}_{{\mathbb {Z}/2}}\to \mathrm {Sp}_{{\mathbb {Z}/2}}$
. We also set
$\mathrm {Sp}_{{\mathbb {Z}/2}}\to \mathrm {Sp}_{{\mathbb {Z}/2}}$
. We also set
![]() $\Sigma ^{m+n\sigma }:=\Sigma ^{m+n\sigma }\mathbb {S}\in \mathrm {Sp}_{{\mathbb {Z}/2}}$
for abbreviation.
$\Sigma ^{m+n\sigma }:=\Sigma ^{m+n\sigma }\mathbb {S}\in \mathrm {Sp}_{{\mathbb {Z}/2}}$
for abbreviation.
For an adjoint pair of
![]() $\infty $
-categories
$\infty $
-categories
![]() $F:\mathcal {C}\rightleftarrows \mathcal {D}:G$
, let
$F:\mathcal {C}\rightleftarrows \mathcal {D}:G$
, let
![]() $ad\colon \mathrm {id} \to GF$
(resp.
$ad\colon \mathrm {id} \to GF$
(resp.
![]() $ad'\colon FG\to \mathrm {id}$
) denote the unit (resp. counit).
$ad'\colon FG\to \mathrm {id}$
) denote the unit (resp. counit).
Lemma 5.1.3. There is a natural equivalence of functors
Proof. Consider the co-Cartesian square of
![]() ${\mathbb {Z}/2}$
-spaces
${\mathbb {Z}/2}$
-spaces

There are
![]() ${\mathbb {Z}/2}$
-homotopy equivalences
${\mathbb {Z}/2}$
-homotopy equivalences
![]() $S^{\sigma }-\{(1,0),(-1,0)\}\simeq {\mathbb {Z}/2}$
and
$S^{\sigma }-\{(1,0),(-1,0)\}\simeq {\mathbb {Z}/2}$
and
![]() $S^{\sigma }-\{(1,0)\}\simeq S^{\sigma }-\{(-1,0)\}\simeq \mathrm {pt}$
. Together with the explicit descriptions of
$S^{\sigma }-\{(1,0)\}\simeq S^{\sigma }-\{(-1,0)\}\simeq \mathrm {pt}$
. Together with the explicit descriptions of
![]() $i_{\sharp }$
and
$i_{\sharp }$
and
![]() $i^*$
in Construction Appendix A.2.4, we obtain a natural equivalence
$i^*$
in Construction Appendix A.2.4, we obtain a natural equivalence
By adjunction, we obtain the desired natural equivalence.
Theorem 5.1.4. For any
![]() $X \in \mathbf {Sch}_{{\mathbb {Z}/2}}$
, there is an equivalence of
$X \in \mathbf {Sch}_{{\mathbb {Z}/2}}$
, there is an equivalence of
![]() ${\mathbb {Z}/2}$
-spectra
${\mathbb {Z}/2}$
-spectra
Proof. As before, we will write the proof as if everything takes place over
![]() $\mathbb {S}$
. Consider the Cartesian equivariant Nisnevich square
$\mathbb {S}$
. Consider the Cartesian equivariant Nisnevich square

as in [Reference Carmody12, Lemma 2.23], where the
![]() ${\mathbb {Z}/2}$
-action on the upper right corner is induced by the action on
${\mathbb {Z}/2}$
-action on the upper right corner is induced by the action on
![]() $\mathbb {P}_{\mathbb {S}}^{\sigma }$
.
$\mathbb {P}_{\mathbb {S}}^{\sigma }$
.
Propositions 2.1.3 and 3.4.7 give equivalences
We similarly have an equivalence
![]() $\mathrm {THR}({\mathbb {Z}/2}\times \mathbb {G}_{m,\mathbb {S}}^{\sigma })\simeq i_*i^*\mathrm {THR}(\mathbb {G}_{m,\mathbb {S}}^{\sigma })$
since there are isomorphisms
$\mathrm {THR}({\mathbb {Z}/2}\times \mathbb {G}_{m,\mathbb {S}}^{\sigma })\simeq i_*i^*\mathrm {THR}(\mathbb {G}_{m,\mathbb {S}}^{\sigma })$
since there are isomorphisms
![]() ${\mathbb {Z}/2}\times \mathbb {G}_{m,\mathbb {S}}^{\sigma } \cong {\mathbb {Z}/2} \times \mathbb {G}_{m,\mathbb {S}}$
and
${\mathbb {Z}/2}\times \mathbb {G}_{m,\mathbb {S}}^{\sigma } \cong {\mathbb {Z}/2} \times \mathbb {G}_{m,\mathbb {S}}$
and
![]() $i^*\mathbb {G}_{m,\mathbb {S}}^{\sigma }\cong i^*\mathbb {G}_{m,\mathbb {S}}$
. The induced map
$i^*\mathbb {G}_{m,\mathbb {S}}^{\sigma }\cong i^*\mathbb {G}_{m,\mathbb {S}}$
. The induced map
![]() $\mathrm {THR}(\mathbb {G}_{m,\mathbb {S}}^{\sigma })\to \mathrm {THR}(\mathbb {Z}/2\times \mathbb {G}_{m,\mathbb {S}}^{\sigma })$
can be identified with the map
$\mathrm {THR}(\mathbb {G}_{m,\mathbb {S}}^{\sigma })\to \mathrm {THR}(\mathbb {Z}/2\times \mathbb {G}_{m,\mathbb {S}}^{\sigma })$
can be identified with the map
obtained by the unit of the adjunction pair
![]() $(i^*,i_*)$
. As in the proof of Theorem 5.1.2, use Propositions 4.2.6, 4.2.8, 4.2.11 and 4.2.12 to see that the induced map
$(i^*,i_*)$
. As in the proof of Theorem 5.1.2, use Propositions 4.2.6, 4.2.8, 4.2.11 and 4.2.12 to see that the induced map
![]() $\mathrm {THR}(\mathbb {A}_{\mathbb {S}}^1)\to \mathrm {THR}(\mathbb {G}_{m,\mathbb {S}})$
can be identified with the map
$\mathrm {THR}(\mathbb {A}_{\mathbb {S}}^1)\to \mathrm {THR}(\mathbb {G}_{m,\mathbb {S}})$
can be identified with the map
obtained by the unit of the adjunction pair
![]() $(i^*,i_*)$
. By equation (4.13), we obtain an equivalence
$(i^*,i_*)$
. By equation (4.13), we obtain an equivalence
Applying
![]() $\mathrm {THR}$
to equation (5.2) and combining with the above discussion yield the following homotopy co-Cartesian square:
$\mathrm {THR}$
to equation (5.2) and combining with the above discussion yield the following homotopy co-Cartesian square:

Consider the commutative square

extracted from equation (5.3), where the right vertical map (resp. lower horizontal map) is obtained by applying
![]() $i_*i^*$
to the left (resp. right) of the unit map
$i_*i^*$
to the left (resp. right) of the unit map
![]() $\mathrm {id} \to i_*i^*$
. Since
$\mathrm {id} \to i_*i^*$
. Since
![]() $\Phi ^{{\mathbb {Z}/2}} i_*\simeq 0$
by Proposition Appendix A.2.7(3),(5),
$\Phi ^{{\mathbb {Z}/2}} i_*\simeq 0$
by Proposition Appendix A.2.7(3),(5),
![]() $\Phi ^{{\mathbb {Z}/2}}Q$
is Cartesian. The objects in the square
$\Phi ^{{\mathbb {Z}/2}}Q$
is Cartesian. The objects in the square
![]() $i^*Q$
are direct sums of
$i^*Q$
are direct sums of
![]() $\bigoplus _{j>0}\Sigma _+^{\infty } S^1$
, and the right vertical and lower horizontal maps are the matrix multiplications given by
$\bigoplus _{j>0}\Sigma _+^{\infty } S^1$
, and the right vertical and lower horizontal maps are the matrix multiplications given by
 $$\begin{align*}\left( \begin{array}{cc} 1 & 0\\ 1 & 0\\ 0 & 1\\ 0 & 1 \end{array} \right) \quad \left( \begin{array}{cc} 1 & 0\\ 0 & 1\\ 0 & 1\\ 1 & 0 \end{array} \right) \end{align*}$$
$$\begin{align*}\left( \begin{array}{cc} 1 & 0\\ 1 & 0\\ 0 & 1\\ 0 & 1 \end{array} \right) \quad \left( \begin{array}{cc} 1 & 0\\ 0 & 1\\ 0 & 1\\ 1 & 0 \end{array} \right) \end{align*}$$
for certain choices of bases. From this, one can check that
![]() $i^*Q$
is Cartesian too. It follows that Q is Cartesian.
$i^*Q$
is Cartesian too. It follows that Q is Cartesian.
Hence, the other direct summand of the square (5.3)

is also Cartesian. It follows that
![]() $\mathrm {THR}(\mathbb {P}_{\mathbb {S}}^{\sigma })$
is equivalent to the direct sum
$\mathrm {THR}(\mathbb {P}_{\mathbb {S}}^{\sigma })$
is equivalent to the direct sum
Together with Lemma 5.1.3, we obtain the desired equivalence.
Proposition 5.1.5. There is an equivalence of
![]() ${\mathbb {Z}/2}$
-spectra
${\mathbb {Z}/2}$
-spectra
5.2 THR of projective spaces
Definition 5.2.1. As usual, for any integer
![]() $n\geq 1$
, we consider the n-cube
$n\geq 1$
, we consider the n-cube
![]() $(\Delta ^1)^n$
as a partially ordered set, and use the same symbol for the associated category. For an
$(\Delta ^1)^n$
as a partially ordered set, and use the same symbol for the associated category. For an
![]() $\infty $
-category
$\infty $
-category
![]() $\mathcal {C}$
, an n-cube in
$\mathcal {C}$
, an n-cube in
![]() $\mathcal {C}$
is a functor
$\mathcal {C}$
is a functor
compare [Reference Lurie42, Definition 6.1.1.2]. If
![]() $\mathcal {C}$
admits limits, the total fiber of Q is defined to be
$\mathcal {C}$
admits limits, the total fiber of Q is defined to be
The following
![]() $\infty $
-categorical result can be shown by dualizing the arguments from [Reference Binda, Park and Østvær8, Proposition A.6.5].
$\infty $
-categorical result can be shown by dualizing the arguments from [Reference Binda, Park and Østvær8, Proposition A.6.5].
Proposition 5.2.2. Let Q be an n-cube in an
![]() $\infty $
-category
$\infty $
-category
![]() $\mathcal {C}$
with small limits, where n is a nonnegative integer. Then for every integer
$\mathcal {C}$
with small limits, where n is a nonnegative integer. Then for every integer
![]() $1\leq i\leq n$
, there exists a fiber sequence
$1\leq i\leq n$
, there exists a fiber sequence
Proposition 5.2.3. Let
![]() $\mathcal {C}$
be a symmetric monoidal stable
$\mathcal {C}$
be a symmetric monoidal stable
![]() $\infty $
-category with small limits such that the tensor product operation on
$\infty $
-category with small limits such that the tensor product operation on
![]() $\mathcal {C}$
preserves fiber sequences in each variable. If Q is an n-cube and
$\mathcal {C}$
preserves fiber sequences in each variable. If Q is an n-cube and
![]() $f\colon X_0\to X_1$
is a map in
$f\colon X_0\to X_1$
is a map in
![]() $\mathcal {C}$
, then there is a canonical equivalence
$\mathcal {C}$
, then there is a canonical equivalence
where
![]() $Q\otimes f$
is the associated
$Q\otimes f$
is the associated
![]() $(n+1)$
-cube sending
$(n+1)$
-cube sending
![]() $(a_1,\ldots ,a_{n+1})\in (\Delta ^1)^{n+1}$
to
$(a_1,\ldots ,a_{n+1})\in (\Delta ^1)^{n+1}$
to
![]() $Q(a_1,\ldots ,a_n)\otimes X_{a_{n+1}}$
.
$Q(a_1,\ldots ,a_n)\otimes X_{a_{n+1}}$
.
Proof. This is again obtained by dualizing the arguments for the corresponding one [Reference Binda, Park and Østvær8, Proposition A.6.7]. An intermediate step is to show
![]() $\mathrm {tfib}(Q)\otimes X\simeq \mathrm {tfib}(Q\otimes X)$
for any
$\mathrm {tfib}(Q)\otimes X\simeq \mathrm {tfib}(Q\otimes X)$
for any
![]() $X\in \mathcal {C}$
, where
$X\in \mathcal {C}$
, where
![]() $Q\otimes X$
is the associated n-cube sending
$Q\otimes X$
is the associated n-cube sending
![]() $(a_1,\ldots ,a_n)\in (\Delta ^1)^n$
to
$(a_1,\ldots ,a_n)\in (\Delta ^1)^n$
to
![]() $Q(a_1,\ldots ,a_n)\otimes X$
. Then one can use Proposition 5.2.2.
$Q(a_1,\ldots ,a_n)\otimes X$
. Then one can use Proposition 5.2.2.
Proposition 5.2.4. Let
![]() $\mathcal {C}$
be a symmetric monoidal stable
$\mathcal {C}$
be a symmetric monoidal stable
![]() $\infty $
-category with small limits such that the tensor product operation on
$\infty $
-category with small limits such that the tensor product operation on
![]() $\mathcal {C}$
preserves fiber sequences in each variable. If
$\mathcal {C}$
preserves fiber sequences in each variable. If
![]() $i_1\colon X_{0,1} \to X_{1,1}$
,
$i_1\colon X_{0,1} \to X_{1,1}$
,
![]() $\ldots $
,
$\ldots $
,
![]() $i_n \colon X_{0,n} \to X_{1,n}$
are maps in
$i_n \colon X_{0,n} \to X_{1,n}$
are maps in
![]() $\mathcal {C}$
, then there is a canonical equivalence
$\mathcal {C}$
, then there is a canonical equivalence
where
![]() $i_1\otimes \cdots \otimes i_n$
is the associated n-cube sending
$i_1\otimes \cdots \otimes i_n$
is the associated n-cube sending
![]() $(a_1,\ldots ,a_n)\in (\Delta ^1)^n$
to
$(a_1,\ldots ,a_n)\in (\Delta ^1)^n$
to
![]() $X_{a_1,1}\otimes \cdots \otimes X_{a_n,n}$
and arrows given by tensor products of
$X_{a_1,1}\otimes \cdots \otimes X_{a_n,n}$
and arrows given by tensor products of
![]() $i_j$
s and identities.
$i_j$
s and identities.
Proof. Use Proposition 5.2.3 repeatedly.
Proposition 5.2.5. Suppose
![]() $X\in \mathbf {Sch}_{{\mathbb {Z}/2}}$
, and let
$X\in \mathbf {Sch}_{{\mathbb {Z}/2}}$
, and let
![]() $\{U_1,\ldots ,U_n\}$
be a Zariski covering of X with the induced involutions. Let Q be the S-cube given by
$\{U_1,\ldots ,U_n\}$
be a Zariski covering of X with the induced involutions. Let Q be the S-cube given by
for nonempty
![]() $\{i_1,\ldots ,i_r\}\subset S:=\{1,\ldots ,n\}$
and
$\{i_1,\ldots ,i_r\}\subset S:=\{1,\ldots ,n\}$
and
![]() $Q(\emptyset ):=X$
. Then there is an equivalence
$Q(\emptyset ):=X$
. Then there is an equivalence
Proof. Let us use the equivalence
![]() $\mathrm {N}(\mathbf {P}(S))\simeq (\Delta ^1)^n$
. We include the description of this equivalence if
$\mathrm {N}(\mathbf {P}(S))\simeq (\Delta ^1)^n$
. We include the description of this equivalence if
![]() $S=\{1\}$
. We regard the partially ordered set
$S=\{1\}$
. We regard the partially ordered set
![]() $\mathbf {P}(\{1\})$
as the category associated with the diagram
$\mathbf {P}(\{1\})$
as the category associated with the diagram
![]() $\emptyset \to \{1\}$
. The nerve of this category is
$\emptyset \to \{1\}$
. The nerve of this category is
![]() $\Delta ^1$
.
$\Delta ^1$
.
We proceed by induction on n. The claim is clear if
![]() $n=1$
. Assume
$n=1$
. Assume
![]() $n>1$
. By induction, we fiber sequences
$n>1$
. By induction, we fiber sequences
and
Together with Proposition 5.2.2, we reduce to showing that the induced square

is Cartesian. This follows from Corollary 3.4.9.
Theorem 5.2.6. For any
![]() $X\in \mathbf {Sch}_{{\mathbb {Z}/2}}$
and integer
$X\in \mathbf {Sch}_{{\mathbb {Z}/2}}$
and integer
![]() $n\geq 0$
, there is an equivalence of
$n\geq 0$
, there is an equivalence of
![]() ${\mathbb {Z}/2}$
-spectra
${\mathbb {Z}/2}$
-spectra
 $$\begin{align*}\mathrm{THR}(X\times \mathbb{P}^{n}) \simeq \left\{ \begin{array}{ll} \mathrm{THR}(X) \oplus \bigoplus_{j=1}^{\lfloor n/2 \rfloor} i_*{\mathrm{THH}}(X) & \text{if } n \text{ is even,} \\ \mathrm{THR}(X) \oplus \bigoplus_{j=1}^{\lfloor n/2 \rfloor} i_*{\mathrm{THH}}(X) \oplus \Sigma^{n(\sigma-1)}\mathrm{THR}(X) & \text{if } n \text{ is odd.} \end{array} \right. \end{align*}$$
$$\begin{align*}\mathrm{THR}(X\times \mathbb{P}^{n}) \simeq \left\{ \begin{array}{ll} \mathrm{THR}(X) \oplus \bigoplus_{j=1}^{\lfloor n/2 \rfloor} i_*{\mathrm{THH}}(X) & \text{if } n \text{ is even,} \\ \mathrm{THR}(X) \oplus \bigoplus_{j=1}^{\lfloor n/2 \rfloor} i_*{\mathrm{THH}}(X) \oplus \Sigma^{n(\sigma-1)}\mathrm{THR}(X) & \text{if } n \text{ is odd.} \end{array} \right. \end{align*}$$
Proof. Proposition Appendix A.2.7(3) allows us to replace
![]() $i_*$
by
$i_*$
by
![]() $i_{\sharp }$
in the claim. We set
$i_{\sharp }$
in the claim. We set
for
![]() $j=1,\ldots ,n$
and
$j=1,\ldots ,n$
and
Observe that there is an isomorphism of commutative monoids
![]() $M_j\cong \mathbb {Z}^{n-1}\oplus \mathbb {N}$
for all
$M_j\cong \mathbb {Z}^{n-1}\oplus \mathbb {N}$
for all
![]() $j=1,\ldots ,n+1$
. We set
$j=1,\ldots ,n+1$
. We set
![]() $M_I:=M_{i_1}\cap \cdots \cap M_{i_q}$
for all nonempty subsets
$M_I:=M_{i_1}\cap \cdots \cap M_{i_q}$
for all nonempty subsets
![]() $I:=\{i_1,\ldots ,i_q\}$
of
$I:=\{i_1,\ldots ,i_q\}$
of
![]() $\{1,\ldots ,n+1\}$
, and consequently
$\{1,\ldots ,n+1\}$
, and consequently
![]() $M_{\emptyset } := \mathbb {Z}^n$
. Together with the obvious maps, we obtain an
$M_{\emptyset } := \mathbb {Z}^n$
. Together with the obvious maps, we obtain an
![]() $(n+1)$
-cube M in commutative monoids associated with
$(n+1)$
-cube M in commutative monoids associated with
![]() $M_I$
for any subset
$M_I$
for any subset
![]() $I\subset \{1,\ldots ,n+1\}$
. Here, we set
$I\subset \{1,\ldots ,n+1\}$
. Here, we set
![]() $M(b_1,...,b_{n+1})=M_I$
, where I is the set of indices i such that
$M(b_1,...,b_{n+1})=M_I$
, where I is the set of indices i such that
![]() $b_i=0$
. By equation (4.4), we have a canonical decomposition
$b_i=0$
. By equation (4.4), we have a canonical decomposition
where
![]() $\mathrm {B}^{\mathrm {di}}(M_I;v):=\emptyset $
if
$\mathrm {B}^{\mathrm {di}}(M_I;v):=\emptyset $
if
![]() $v\notin M_I$
. Hence, for every v the above
$v\notin M_I$
. Hence, for every v the above
![]() $\mathrm {B}^{\mathrm {di}}(M_I;v)$
assemble to an
$\mathrm {B}^{\mathrm {di}}(M_I;v)$
assemble to an
![]() $(n+1)$
-cube in
$(n+1)$
-cube in
![]() ${\mathbb {Z}/2}$
-spaces, and a decomposition of the
${\mathbb {Z}/2}$
-spaces, and a decomposition of the
![]() $(n+1)$
-cube
$(n+1)$
-cube
![]() $\mathrm {B}^{\mathrm {di}} M$
into these smaller cubes as v varies in
$\mathrm {B}^{\mathrm {di}} M$
into these smaller cubes as v varies in
![]() $\mathbb {Z}^n$
. Combine Propositions 4.2.4 and 4.2.12 to show that the induced map in this cube
$\mathbb {Z}^n$
. Combine Propositions 4.2.4 and 4.2.12 to show that the induced map in this cube
is an equivalence for every integer
![]() $0\leq s\leq n-1$
if the first coordinate of v is greater than
$0\leq s\leq n-1$
if the first coordinate of v is greater than
![]() $0$
. By a change of coordinates in the target, we see that the induced map
$0$
. By a change of coordinates in the target, we see that the induced map
is an equivalence for all
![]() $j=1,\ldots ,n+1$
, subsets I of
$j=1,\ldots ,n+1$
, subsets I of
![]() $\{1,\ldots ,n+1\}-\{j\}$
and
$\{1,\ldots ,n+1\}-\{j\}$
and
![]() $v\in M_j^+$
, where
$v\in M_j^+$
, where
![]() $M_j^+$
denotes the set of nonunits of
$M_j^+$
denotes the set of nonunits of
![]() $M_j$
. Use Proposition 5.2.2 repeatedly to show
$M_j$
. Use Proposition 5.2.2 repeatedly to show
for all
![]() $v\in M_j^+$
. This means
$v\in M_j^+$
. This means
![]() $\mathrm {tfib}(\mathbb {S}[\mathrm {B}^{\mathrm {di}}(M;v)])\simeq 0$
whenever
$\mathrm {tfib}(\mathbb {S}[\mathrm {B}^{\mathrm {di}}(M;v)])\simeq 0$
whenever
![]() $v\neq O$
since
$v\neq O$
since
![]() $M_{\emptyset }-(M_1^+\cup \cdots \cup M_{n+1}^+)=\{O\}$
, where O denotes the origin in
$M_{\emptyset }-(M_1^+\cup \cdots \cup M_{n+1}^+)=\{O\}$
, where O denotes the origin in
![]() $\mathbb {Z}^n$
.
$\mathbb {Z}^n$
.
Now consider the standard cover of
![]() $\mathbb {P}^n_{\mathbb {S}}$
by
$\mathbb {P}^n_{\mathbb {S}}$
by
![]() $(n+1)$
copies of
$(n+1)$
copies of
![]() $\mathbb {A}^n_{\mathbb {S}}$
, and recall that
$\mathbb {A}^n_{\mathbb {S}}$
, and recall that
![]() $\mathbb {A}^n_{\mathbb {S}}$
is the spherical monoid ring of
$\mathbb {A}^n_{\mathbb {S}}$
is the spherical monoid ring of
![]() $\mathbb {N}^n$
. (We continue switching between spherical monoid rings and honest schemes over rings as before. Also, note that by Proposition 4.2.15 products of affine schemes correspond to products of monoids when computing
$\mathbb {N}^n$
. (We continue switching between spherical monoid rings and honest schemes over rings as before. Also, note that by Proposition 4.2.15 products of affine schemes correspond to products of monoids when computing
![]() $\mathrm {THR}$
.) Choosing suitable coordinates, the intersections of s elements of the cover with
$\mathrm {THR}$
.) Choosing suitable coordinates, the intersections of s elements of the cover with
![]() $0<s\leq n+1$
are given by (the spherical monoid rings of)
$0<s\leq n+1$
are given by (the spherical monoid rings of)
![]() $M_I$
above such that
$M_I$
above such that
![]() $\lvert I \rvert = n+1-s$
. By Proposition 5.2.5, we have an equivalence
$\lvert I \rvert = n+1-s$
. By Proposition 5.2.5, we have an equivalence
Together with equation (5.5), we have an equivalence
since
![]() $\mathrm {B}^{\mathrm {di}}(M_{\{1,\ldots ,n\}};O)\cong \mathrm {B}^{\mathrm {di}}(M_{\{1,\ldots ,n\}})$
. For every subset I of
$\mathrm {B}^{\mathrm {di}}(M_{\{1,\ldots ,n\}};O)\cong \mathrm {B}^{\mathrm {di}}(M_{\{1,\ldots ,n\}})$
. For every subset I of
![]() $\{1,\ldots ,n\}$
, we have the canonical decomposition
$\{1,\ldots ,n\}$
, we have the canonical decomposition
where
![]() $V_I$
is obtained by removing the base point
$V_I$
is obtained by removing the base point
![]() $*$
of
$*$
of
![]() $\mathrm {B}^{\mathrm {di}}(M_I;O)$
corresponding to the element
$\mathrm {B}^{\mathrm {di}}(M_I;O)$
corresponding to the element
![]() $0\in M_I$
in simplicial degree
$0\in M_I$
in simplicial degree
![]() $0$
. This yields the canonical decomposition
$0$
. This yields the canonical decomposition
where every entry of
![]() $Q'$
is
$Q'$
is
![]() $\Sigma ^{\infty }_+ * \simeq \mathbb {S}$
. Use Proposition 5.2.2 repeatedly to have an equivalence
$\Sigma ^{\infty }_+ * \simeq \mathbb {S}$
. Use Proposition 5.2.2 repeatedly to have an equivalence
![]() $\mathrm {tfib}(Q') \simeq 0$
. This implies that we have an equivalence
$\mathrm {tfib}(Q') \simeq 0$
. This implies that we have an equivalence
On the other hand, we have
![]() $Q(0,\ldots ,0)=0$
since
$Q(0,\ldots ,0)=0$
since
![]() $M_{\{1,\ldots ,n\}}=0$
. This implies that we have an equivalence
$M_{\{1,\ldots ,n\}}=0$
. This implies that we have an equivalence
Combine what we have discussed above to have an equivalence
We claim that
 $$\begin{align*}\mathrm{tfib}(Q|_{(\Delta^1)^{d+1}\times \{0\}^{n-d}}) \simeq \left\{ \begin{array}{ll} \bigoplus_{j=1}^{\lfloor d/2 \rfloor} i_{\sharp}\Sigma^{-1} & \text{if } d \text{ is even}, \\ \bigoplus_{j=1}^{\lfloor d/2 \rfloor} i_{\sharp}\Sigma^{-1} \oplus \Sigma^{d\sigma-d-1}& \text{if } d \text{ is odd}. \end{array} \right. \end{align*}$$
$$\begin{align*}\mathrm{tfib}(Q|_{(\Delta^1)^{d+1}\times \{0\}^{n-d}}) \simeq \left\{ \begin{array}{ll} \bigoplus_{j=1}^{\lfloor d/2 \rfloor} i_{\sharp}\Sigma^{-1} & \text{if } d \text{ is even}, \\ \bigoplus_{j=1}^{\lfloor d/2 \rfloor} i_{\sharp}\Sigma^{-1} \oplus \Sigma^{d\sigma-d-1}& \text{if } d \text{ is odd}. \end{array} \right. \end{align*}$$
Let us proceed by induction on d. The claim is clear if
![]() $d=0$
by the definition of the total fiber. Assume
$d=0$
by the definition of the total fiber. Assume
![]() $0<d\leq n$
. Let
$0<d\leq n$
. Let
![]() $\{e_1,\ldots ,e_n\}$
be the standard basis in
$\{e_1,\ldots ,e_n\}$
be the standard basis in
![]() $\mathbb {Z}^n$
. The d-cube
$\mathbb {Z}^n$
. The d-cube
![]() $M|_{(\Delta ^1)^{d} \times \{1\} \times \{0\}^{n-d}}$
is isomorphic to the naturally associated d-cube sending
$M|_{(\Delta ^1)^{d} \times \{1\} \times \{0\}^{n-d}}$
is isomorphic to the naturally associated d-cube sending
![]() $(a_1,\ldots ,a_d)\in (\Delta ^1)^d$
to
$(a_1,\ldots ,a_d)\in (\Delta ^1)^d$
to
where
![]() $P_0:=\mathbb {N}$
,
$P_0:=\mathbb {N}$
,
![]() $P_1:=\mathbb {Z}$
and
$P_1:=\mathbb {Z}$
and
![]() $e_{n+1}:=0$
. Combine Propositions 4.2.5 and 5.2.4 to obtain an equivalence
$e_{n+1}:=0$
. Combine Propositions 4.2.5 and 5.2.4 to obtain an equivalence
 $$ \begin{align*} &\mathrm{tfib}(\mathbb{S}[\mathrm{B}^{\mathrm{di}}(M|_{(\Delta^1)^{d}\times \{1\} \times \{0\}^{n-d}};O)]) \\ \simeq & \mathrm{fib}(\mathbb{S}[\mathrm{B}^{\mathrm{di}}(\mathbb{N};0)]\to \mathbb{S}[\mathrm{B}^{\mathrm{di}}(\mathbb{Z};0)])^{\wedge d} \wedge \mathbb{S}[\mathrm{B}^{\mathrm{di}}(\mathbb{N};0)]^{\wedge n-d}. \end{align*} $$
$$ \begin{align*} &\mathrm{tfib}(\mathbb{S}[\mathrm{B}^{\mathrm{di}}(M|_{(\Delta^1)^{d}\times \{1\} \times \{0\}^{n-d}};O)]) \\ \simeq & \mathrm{fib}(\mathbb{S}[\mathrm{B}^{\mathrm{di}}(\mathbb{N};0)]\to \mathbb{S}[\mathrm{B}^{\mathrm{di}}(\mathbb{Z};0)])^{\wedge d} \wedge \mathbb{S}[\mathrm{B}^{\mathrm{di}}(\mathbb{N};0)]^{\wedge n-d}. \end{align*} $$
Use Proposition 5.2.2 repeatedly to deduce an equivalence
Together with Proposition 4.2.11 and equation (4.12), we obtain equivalences
 $$ \begin{align*} \mathrm{tfib}(Q|_{(\Delta^1)^{d}\times \{1\} \times \{0\}^{n-d}}) \simeq & \mathrm{fib}(\mathbb{S} \to \mathbb{S}[S^{\sigma}])^{\wedge d} \wedge \mathbb{S}^{\wedge n-d} \\ \simeq & \Sigma^{-d} (\Sigma^{\infty} S^{\sigma}/(1,0))^{\wedge d} \simeq \Sigma^{d\sigma-d}, \end{align*} $$
$$ \begin{align*} \mathrm{tfib}(Q|_{(\Delta^1)^{d}\times \{1\} \times \{0\}^{n-d}}) \simeq & \mathrm{fib}(\mathbb{S} \to \mathbb{S}[S^{\sigma}])^{\wedge d} \wedge \mathbb{S}^{\wedge n-d} \\ \simeq & \Sigma^{-d} (\Sigma^{\infty} S^{\sigma}/(1,0))^{\wedge d} \simeq \Sigma^{d\sigma-d}, \end{align*} $$
where
![]() $(1,0)$
is the base point of
$(1,0)$
is the base point of
![]() $S^{\sigma }$
. Proposition 5.2.2 gives a fiber sequence
$S^{\sigma }$
. Proposition 5.2.2 gives a fiber sequence
If d is odd, then we obtain a fiber sequence
 $$ \begin{align} \mathrm{tfib}(Q|_{(\Delta^1)^{d+1}\times \{0\}^{n-d}}) \to \bigoplus_{j=1}^{\lfloor d/2 \rfloor} i_{\sharp}\Sigma^{-1} \xrightarrow{f} \Sigma^{d\sigma-d} \end{align} $$
$$ \begin{align} \mathrm{tfib}(Q|_{(\Delta^1)^{d+1}\times \{0\}^{n-d}}) \to \bigoplus_{j=1}^{\lfloor d/2 \rfloor} i_{\sharp}\Sigma^{-1} \xrightarrow{f} \Sigma^{d\sigma-d} \end{align} $$
by induction. Since
![]() $\pi _{-1}(\Sigma ^0)=0$
, the map
$\pi _{-1}(\Sigma ^0)=0$
, the map
![]() $\Sigma ^{-1}\to i^*\Sigma ^{d\sigma -d}\simeq \Sigma ^0$
obtained by adjunction is equivalent to
$\Sigma ^{-1}\to i^*\Sigma ^{d\sigma -d}\simeq \Sigma ^0$
obtained by adjunction is equivalent to
![]() $0$
. It follows that f is equivalent to
$0$
. It follows that f is equivalent to
![]() $0$
, that is, equation (5.7) splits. This completes the induction argument for odd d.
$0$
, that is, equation (5.7) splits. This completes the induction argument for odd d.
If d is even, we obtain a fiber sequence
 $$\begin{align*}\mathrm{tfib}(Q|_{(\Delta^1)^{d+1}\times \{0\}^{n-d}}) \to \bigoplus_{j=1}^{\lfloor d/2 \rfloor-1} i_{\sharp}\Sigma^{-1} \oplus \Sigma^{(d-1)\sigma-d} \to \Sigma^{d\sigma-d} \end{align*}$$
$$\begin{align*}\mathrm{tfib}(Q|_{(\Delta^1)^{d+1}\times \{0\}^{n-d}}) \to \bigoplus_{j=1}^{\lfloor d/2 \rfloor-1} i_{\sharp}\Sigma^{-1} \oplus \Sigma^{(d-1)\sigma-d} \to \Sigma^{d\sigma-d} \end{align*}$$
by induction. As above, the induced map
![]() $\bigoplus _{j=1}^{\lfloor d/2 \rfloor -1} i_{\sharp }\Sigma ^{-1} \to \Sigma ^{d\sigma -d}$
is equivalent to
$\bigoplus _{j=1}^{\lfloor d/2 \rfloor -1} i_{\sharp }\Sigma ^{-1} \to \Sigma ^{d\sigma -d}$
is equivalent to
![]() $0$
. It follows that we have an equivalence
$0$
. It follows that we have an equivalence
 $$\begin{align*}\mathrm{tfib}(Q|_{(\Delta^1)^{d+1}\times \{0\}^{n-d}}) \simeq \bigoplus_{j=1}^{\lfloor d/2 \rfloor-1} i_{\sharp}\Sigma^{-1} \oplus \mathrm{fib}(\Sigma^{(d-1)\sigma-d}\xrightarrow{g}\Sigma^{d\sigma-d}). \end{align*}$$
$$\begin{align*}\mathrm{tfib}(Q|_{(\Delta^1)^{d+1}\times \{0\}^{n-d}}) \simeq \bigoplus_{j=1}^{\lfloor d/2 \rfloor-1} i_{\sharp}\Sigma^{-1} \oplus \mathrm{fib}(\Sigma^{(d-1)\sigma-d}\xrightarrow{g}\Sigma^{d\sigma-d}). \end{align*}$$
We now analyze the nontrivial map
![]() $g\colon \Sigma ^{(d-1)\sigma -d} \to \Sigma ^{d\sigma -d}$
. On the level of commutative monoids, this corresponds to the inclusion
$g\colon \Sigma ^{(d-1)\sigma -d} \to \Sigma ^{d\sigma -d}$
. On the level of commutative monoids, this corresponds to the inclusion
 $$ \begin{align*} &\mathbb{Z} (u_1-u_d)\oplus \cdots \oplus \mathbb{Z} (u_{d-1}-u_d) \oplus \mathbb{N}(-e_d) \oplus \mathbb{N}(e_{d+1}-e_d) \oplus \cdots \oplus \mathbb{N}(e_n-e_d) \\ \to & \mathbb{Z} u_1\oplus \cdots \oplus \mathbb{Z} u_d \oplus \mathbb{N} u_{d+1} \oplus \cdots \oplus \mathbb{N} u_{n}, \end{align*} $$
$$ \begin{align*} &\mathbb{Z} (u_1-u_d)\oplus \cdots \oplus \mathbb{Z} (u_{d-1}-u_d) \oplus \mathbb{N}(-e_d) \oplus \mathbb{N}(e_{d+1}-e_d) \oplus \cdots \oplus \mathbb{N}(e_n-e_d) \\ \to & \mathbb{Z} u_1\oplus \cdots \oplus \mathbb{Z} u_d \oplus \mathbb{N} u_{d+1} \oplus \cdots \oplus \mathbb{N} u_{n}, \end{align*} $$
where
![]() $u_i:=e_i-e_{d+1}$
for
$u_i:=e_i-e_{d+1}$
for
![]() $i\in \{1,\ldots ,n\}-\{d+1\}$
and
$i\in \{1,\ldots ,n\}-\{d+1\}$
and
![]() $u_{d+1}:=e_{d+1}$
. As the
$u_{d+1}:=e_{d+1}$
. As the
![]() $0$
-entry for
$0$
-entry for
![]() $\mathrm {B}^{\mathrm {di}} \mathbb {N}$
is just a point, we only need to study the homomorphism
$\mathrm {B}^{\mathrm {di}} \mathbb {N}$
is just a point, we only need to study the homomorphism
![]() $\mathbb {Z}^{d-1}\to \mathbb {Z}^d$
given by
$\mathbb {Z}^{d-1}\to \mathbb {Z}^d$
given by
In the degree
![]() $(0,\ldots ,0)$
, this is easily seen to induce via Proposition 4.2.8 the map
$(0,\ldots ,0)$
, this is easily seen to induce via Proposition 4.2.8 the map
![]() $(S^{\sigma })^{\times d-1} \to (S^{\sigma })^{\times d}$
given by
$(S^{\sigma })^{\times d-1} \to (S^{\sigma })^{\times d}$
given by
After a further cancellation of base points, we are left with studying the map
![]() $h\colon (S^{\sigma })^{\wedge d-1}\to (S^{\sigma })^{\wedge d}$
. This is an equivariant cofibration, as it is the
$h\colon (S^{\sigma })^{\wedge d-1}\to (S^{\sigma })^{\wedge d}$
. This is an equivariant cofibration, as it is the
![]() $(S^{\sigma })^{\wedge d-1}$
-suspension of the pushout of the cofibration
$(S^{\sigma })^{\wedge d-1}$
-suspension of the pushout of the cofibration
![]() $G \times S^{0} \to G \times I$
along the projection
$G \times S^{0} \to G \times I$
along the projection
![]() $G \times S^0 \to (G/G) \times S^0$
. Hence, unstably the equivariant (homotopy) cofiber of f is given by
$G \times S^0 \to (G/G) \times S^0$
. Hence, unstably the equivariant (homotopy) cofiber of f is given by
![]() $(S^{\sigma })^{\wedge d}/h((S^{\sigma })^{\wedge d-1})\simeq S^d \vee S^d$
, where
$(S^{\sigma })^{\wedge d}/h((S^{\sigma })^{\wedge d-1})\simeq S^d \vee S^d$
, where
![]() $G={\mathbb {Z}/2}$
acts on the latter by switching the spheres. Thus the stable equivariant (homotopy) fiber
$G={\mathbb {Z}/2}$
acts on the latter by switching the spheres. Thus the stable equivariant (homotopy) fiber
![]() $\mathrm {fib}(g)$
is given by
$\mathrm {fib}(g)$
is given by
![]() $\Sigma ^{-d-1}\Sigma ^{\infty }(S^{d} \vee S^{d}) \simeq i_{\sharp } \Sigma ^{-1}$
using equation (A.15). This completes the induction argument for even d.
$\Sigma ^{-d-1}\Sigma ^{\infty }(S^{d} \vee S^{d}) \simeq i_{\sharp } \Sigma ^{-1}$
using equation (A.15). This completes the induction argument for even d.
Together with equation (5.6), we obtain an equivalence
 $$\begin{align*}\mathrm{THR}(\mathbb{P}_{\mathbb{S}}^{n}) \simeq \left\{ \begin{array}{ll} \mathbb{S} \oplus \bigoplus_{j=1}^{\lfloor n/2 \rfloor} i_{\sharp}\mathbb{S} &\text{if } n \text{ is even,}\\ \mathbb{S} \oplus \bigoplus_{j=1}^{\lfloor n/2 \rfloor} i_{\sharp}\mathbb{S} \oplus \Sigma^{n(\sigma-1)} &\text{if } n \text{ is odd.} \end{array} \right. \end{align*}$$
$$\begin{align*}\mathrm{THR}(\mathbb{P}_{\mathbb{S}}^{n}) \simeq \left\{ \begin{array}{ll} \mathbb{S} \oplus \bigoplus_{j=1}^{\lfloor n/2 \rfloor} i_{\sharp}\mathbb{S} &\text{if } n \text{ is even,}\\ \mathbb{S} \oplus \bigoplus_{j=1}^{\lfloor n/2 \rfloor} i_{\sharp}\mathbb{S} \oplus \Sigma^{n(\sigma-1)} &\text{if } n \text{ is odd.} \end{array} \right. \end{align*}$$
Use Propositions 4.2.15 and 5.2.5 for the standard cover of
![]() $\mathbb {P}^n$
to obtain an equivalence
$\mathbb {P}^n$
to obtain an equivalence
whenever X is an affine scheme with involution. Use Proposition 5.2.5 again to generalize this equivalence to the case when X is a separated scheme with involution. Hence, to obtain the desired equivalence, it suffices to obtain an equivalence
Note that this result is compatible with the projective bundle theorem for the oriented theory
![]() ${\mathrm {THH}}$
, see [Reference Blumberg and Mandell10], after applying
${\mathrm {THH}}$
, see [Reference Blumberg and Mandell10], after applying
![]() $i^*$
and using Propositions 3.4.7 and Appendix A.2.7.
$i^*$
and using Propositions 3.4.7 and Appendix A.2.7.
For all
![]() $X\in \mathbf {Sch}_{{\mathbb {Z}/2}}$
and integers m, we set
$X\in \mathbf {Sch}_{{\mathbb {Z}/2}}$
and integers m, we set
Recall that
![]() $(-)^{{\mathbb {Z}/2}}$
commutes with
$(-)^{{\mathbb {Z}/2}}$
commutes with
![]() $\Sigma ^1$
but not with
$\Sigma ^1$
but not with
![]() $\Sigma ^{\sigma }$
.
$\Sigma ^{\sigma }$
.
Looking at fixed points, the result becomes
 $$ \begin{align} \mathrm{THO}^{[m]}(X\times \mathbb{P}^{n}) \simeq \left\{ \begin{array}{ll} \mathrm{THO}^{[m]}(X) \oplus \bigoplus_{j=1}^{\lfloor n/2 \rfloor} {\mathrm{THH}}(X) & \text{if } n \text{ is even,} \\ \mathrm{THO}^{[m]}(X) \oplus \bigoplus_{j=1}^{\lfloor n/2 \rfloor} {\mathrm{THH}}(X) \oplus \mathrm{THO}^{[m-n]}(X) & \text{if } n \text{ is odd.} \end{array} \right. \end{align} $$
$$ \begin{align} \mathrm{THO}^{[m]}(X\times \mathbb{P}^{n}) \simeq \left\{ \begin{array}{ll} \mathrm{THO}^{[m]}(X) \oplus \bigoplus_{j=1}^{\lfloor n/2 \rfloor} {\mathrm{THH}}(X) & \text{if } n \text{ is even,} \\ \mathrm{THO}^{[m]}(X) \oplus \bigoplus_{j=1}^{\lfloor n/2 \rfloor} {\mathrm{THH}}(X) \oplus \mathrm{THO}^{[m-n]}(X) & \text{if } n \text{ is odd.} \end{array} \right. \end{align} $$
Remark 5.2.7. As for
![]() $n=1$
in the previous subsection, the formula for
$n=1$
in the previous subsection, the formula for
![]() $\mathrm {THO}(X\times \mathbb {P}^n)$
corresponds to the one for
$\mathrm {THO}(X\times \mathbb {P}^n)$
corresponds to the one for
![]() $\mathbf {KO}(X\times \mathbb {P}^n)$
. Indeed, for higher-dimensional projective spaces
$\mathbf {KO}(X\times \mathbb {P}^n)$
. Indeed, for higher-dimensional projective spaces
![]() $\mathbb {P}^n$
with trivial involution,
$\mathbb {P}^n$
with trivial involution,
![]() $\mathbf {KO}=\mathbf {KR}$
has been recently computed by [Reference Rohrbach50] and [Reference Karoubi, Schlichting and Weibel36]. Analyzing the arguments of [Reference Rohrbach50], one sees that for even n the results for
$\mathbf {KO}=\mathbf {KR}$
has been recently computed by [Reference Rohrbach50] and [Reference Karoubi, Schlichting and Weibel36]. Analyzing the arguments of [Reference Rohrbach50], one sees that for even n the results for
![]() $\mathbf {KR}(\mathbb {P}^n)$
with and without involution are the same. However, when trying to compute
$\mathbf {KR}(\mathbb {P}^n)$
with and without involution are the same. However, when trying to compute
![]() $\mathrm {THR}$
of higher-dimensional
$\mathrm {THR}$
of higher-dimensional
![]() $\mathbb {P}^n$
with involution, the standard cover of
$\mathbb {P}^n$
with involution, the standard cover of
![]() $\mathbb {P}^n$
will not respect the involution. For the one-dimensional
$\mathbb {P}^n$
will not respect the involution. For the one-dimensional
![]() $\mathbb {P}^{\sigma }$
we used the square in equation (5.2) instead, and for
$\mathbb {P}^{\sigma }$
we used the square in equation (5.2) instead, and for
![]() $(\mathbb {P}^n,\tau )$
in general one would have to construct more complicated cubes that respect the involution
$(\mathbb {P}^n,\tau )$
in general one would have to construct more complicated cubes that respect the involution
![]() $\tau $
.
$\tau $
.
Appendix A Equivariant homotopy theory
The purpose of this appendix is to review equivariant homotopy theory. Throughout this section, G is a finite group.
A.1
 $\infty $
-categories of equivariant spectra
$\infty $
-categories of equivariant spectra
In this subsection, we review the
![]() $\infty $
-categorical formulation of equivariant homotopy theory following Bachmann and Hoyois [Reference Bachmann and Hoyois4]. We restrict to finite groupoids, although Bachmann and Hoyois deal more generally with profinite groupoids. This approach will be compared to more classical references like [Reference Hill, Hopkins and Ravenel29] in Section Appendix A.2 below.
$\infty $
-categorical formulation of equivariant homotopy theory following Bachmann and Hoyois [Reference Bachmann and Hoyois4]. We restrict to finite groupoids, although Bachmann and Hoyois deal more generally with profinite groupoids. This approach will be compared to more classical references like [Reference Hill, Hopkins and Ravenel29] in Section Appendix A.2 below.
Definition Appendix A.1.1. Let
![]() $\mathrm {FinGpd}$
denote the
$\mathrm {FinGpd}$
denote the
![]() $2$
-category of finite groupoids, that is those with only finitely many objects and morphisms. A morphism in
$2$
-category of finite groupoids, that is those with only finitely many objects and morphisms. A morphism in
![]() $\mathrm {FinGpd}$
is called a finite covering if its fibers (which by our assumptions have only finitely many objects) automatically are sets, that is, do not have nontrivial automorphisms. Recall that the fiber of a
$\mathrm {FinGpd}$
is called a finite covering if its fibers (which by our assumptions have only finitely many objects) automatically are sets, that is, do not have nontrivial automorphisms. Recall that the fiber of a
![]() $1$
-morphism
$1$
-morphism
![]() $f\colon Y\to X$
over a point
$f\colon Y\to X$
over a point
![]() $*$
in X is
$*$
in X is
![]() $Y\times _X *$
. For
$Y\times _X *$
. For
![]() $X\in \mathrm {FinGpd}$
, let
$X\in \mathrm {FinGpd}$
, let
![]() $\mathrm {Fin}_X$
denote the category of finite coverings of X. There is an equivalence between
$\mathrm {Fin}_X$
denote the category of finite coverings of X. There is an equivalence between
![]() $\mathrm {Fin}_{\mathrm {B} G}$
and the category of finite G-sets by [Reference Bachmann and Hoyois4, Lemma 9.3].
$\mathrm {Fin}_{\mathrm {B} G}$
and the category of finite G-sets by [Reference Bachmann and Hoyois4, Lemma 9.3].
For a morphism
![]() $f\colon Y\to X$
in
$f\colon Y\to X$
in
![]() $\mathrm {FinGpd}$
, there is an adjunction
$\mathrm {FinGpd}$
, there is an adjunction
where
![]() $f^*$
sends
$f^*$
sends
![]() $V\in \mathrm {Fin}_X$
to
$V\in \mathrm {Fin}_X$
to
![]() $V\times _X Y$
. If f is a finite covering, then there is an adjunction
$V\times _X Y$
. If f is a finite covering, then there is an adjunction
where
![]() $f_{\sharp }$
sends
$f_{\sharp }$
sends
![]() $V\in \mathrm {Fin}_Y$
to V, compare the paragraph preceding [Reference Bachmann and Hoyois4, section 9.2].
$V\in \mathrm {Fin}_Y$
to V, compare the paragraph preceding [Reference Bachmann and Hoyois4, section 9.2].
Example Appendix A.1.2. If i is the obvious morphism of groupoids
![]() $\mathrm {pt}\to \mathrm {B} G$
, then
$\mathrm {pt}\to \mathrm {B} G$
, then
![]() $i_{\sharp }E=\coprod _G E$
and
$i_{\sharp }E=\coprod _G E$
and
![]() $(i_{\sharp },i^*)$
is the usual free-forgetful adjunction between sets and G-sets. On the other hand, for any finite set E the G-set
$(i_{\sharp },i^*)$
is the usual free-forgetful adjunction between sets and G-sets. On the other hand, for any finite set E the G-set
![]() $i_*E$
is isomorphic to
$i_*E$
is isomorphic to
![]() $\prod _G E$
with G acting by permuting the indices.
$\prod _G E$
with G acting by permuting the indices.
For
![]() $p:\mathrm {B} G\to \mathrm {pt}$
, we have
$p:\mathrm {B} G\to \mathrm {pt}$
, we have
![]() $p_* E = E^G$
for every finite G-set E. Note that
$p_* E = E^G$
for every finite G-set E. Note that
![]() $p_{\sharp } E$
is not defined as p is not a finite covering, although for finite G-sets E the left adjoint to
$p_{\sharp } E$
is not defined as p is not a finite covering, although for finite G-sets E the left adjoint to
![]() $p^*$
exists, and is given by the orbit set
$p^*$
exists, and is given by the orbit set
![]() $E/G$
.
$E/G$
.
Definition Appendix A.1.3. For a category
![]() $\mathcal {C}$
with pullbacks, let
$\mathcal {C}$
with pullbacks, let
![]() $\mathrm {Span}(\mathcal {C})$
denote the category of spans, whose objects are the same as
$\mathrm {Span}(\mathcal {C})$
denote the category of spans, whose objects are the same as
![]() $\mathcal {C}$
, whose morphisms are given by the diagrams
$\mathcal {C}$
, whose morphisms are given by the diagrams
![]() $(X\xleftarrow {f} Y \xrightarrow {p} Z)$
in
$(X\xleftarrow {f} Y \xrightarrow {p} Z)$
in
![]() $\mathcal {C}$
, and whose compositions of morphisms are given by pullbacks. A morphism
$\mathcal {C}$
, and whose compositions of morphisms are given by pullbacks. A morphism
![]() $(X\xleftarrow {f} Y \xrightarrow {p} Z)$
is called a forward morphism (resp. backward morphism) if
$(X\xleftarrow {f} Y \xrightarrow {p} Z)$
is called a forward morphism (resp. backward morphism) if
![]() $f=\mathrm {id}$
(resp.
$f=\mathrm {id}$
(resp.
![]() $p=\mathrm {id}$
). The notion of spans can be generalized to the case when
$p=\mathrm {id}$
). The notion of spans can be generalized to the case when
![]() $\mathcal {C}$
is an
$\mathcal {C}$
is an
![]() $\infty $
-category; see [Reference Barwick5, section 5] for the details.
$\infty $
-category; see [Reference Barwick5, section 5] for the details.
Construction Appendix A.1.4. In [Reference Bachmann and Hoyois4, section 9.2], Bachmann and Hoyois construct three functors
![]() $\mathcal {H}, \mathcal {H}_{\bullet }$
and
$\mathcal {H}, \mathcal {H}_{\bullet }$
and
![]() $\mathcal {SH}$
on
$\mathcal {SH}$
on
![]() $\mathrm {FinGpd}$
by certain presheaves on
$\mathrm {FinGpd}$
by certain presheaves on
![]() $\mathrm {Fin}_X$
, and then further refine these to functors
$\mathrm {Fin}_X$
, and then further refine these to functors
together with natural transformations
Let us explain parts of their construction.
For an
![]() $\infty $
-category
$\infty $
-category
![]() $\mathcal {C}$
with finite coproducts, let
$\mathcal {C}$
with finite coproducts, let
![]() $\mathcal {P}_{\Sigma }(\mathcal {C})$
denote the
$\mathcal {P}_{\Sigma }(\mathcal {C})$
denote the
![]() $\infty $
-category of presheaves of spaces which transform finite coproducts into finite products. For
$\infty $
-category of presheaves of spaces which transform finite coproducts into finite products. For
![]() $X\in \mathrm {FinGpd}$
, we set
$X\in \mathrm {FinGpd}$
, we set
![]() $\mathcal {H}(X):=\mathcal {P}_{\Sigma }(\mathrm {Fin}_X)$
. Then we set
$\mathcal {H}(X):=\mathcal {P}_{\Sigma }(\mathrm {Fin}_X)$
. Then we set
![]() $\mathcal {H}_{\bullet }(X):=\mathcal {H}(X)_*$
, which is the
$\mathcal {H}_{\bullet }(X):=\mathcal {H}(X)_*$
, which is the
![]() $\infty $
-category of pointed objects in
$\infty $
-category of pointed objects in
![]() $\mathcal {H}(X)$
. As claimed in [Reference Bachmann and Hoyois4, p. 81], for
$\mathcal {H}(X)$
. As claimed in [Reference Bachmann and Hoyois4, p. 81], for
![]() $X=\mathrm {B} G$
these yield the usual
$X=\mathrm {B} G$
these yield the usual
![]() $\infty $
-categories of G-spaces and pointed G-spaces.
$\infty $
-categories of G-spaces and pointed G-spaces.
For a morphism
![]() $f\colon Y\to X$
, the functor
$f\colon Y\to X$
, the functor
![]() $f^*$
for
$f^*$
for
![]() $\mathcal {H}$
and
$\mathcal {H}$
and
![]() $\mathcal {H}_{\bullet }$
is induced by equation (A.1), and
$\mathcal {H}_{\bullet }$
is induced by equation (A.1), and
![]() $f^*$
admits a right adjoint
$f^*$
admits a right adjoint
![]() $f_*$
. For
$f_*$
. For
![]() $\mathcal {H}_{\bullet }$
,
$\mathcal {H}_{\bullet }$
,
![]() $f_{\otimes }$
is a symmetric monoidal functor preserving sifted colimits such that
$f_{\otimes }$
is a symmetric monoidal functor preserving sifted colimits such that
![]() $f_{\otimes }(V_+)\simeq f_*(V)_+$
for
$f_{\otimes }(V_+)\simeq f_*(V)_+$
for
![]() $V\in \mathrm {Fin}_X$
. If f is a finite covering,
$V\in \mathrm {Fin}_X$
. If f is a finite covering,
![]() $f^*$
for
$f^*$
for
![]() $\mathcal {H}$
and
$\mathcal {H}$
and
![]() $\mathcal {H}_{\bullet }$
admits a left adjoint
$\mathcal {H}_{\bullet }$
admits a left adjoint
![]() $f_{\sharp }$
.
$f_{\sharp }$
.
We obtain
![]() $\mathcal {SH}(X)$
from
$\mathcal {SH}(X)$
from
![]() $\mathcal {H}_{\bullet }(X)$
by
$\mathcal {H}_{\bullet }(X)$
by
![]() $\otimes $
-inverting
$\otimes $
-inverting
![]() $p_{\otimes }(S^1)$
for all finite coverings
$p_{\otimes }(S^1)$
for all finite coverings
![]() $p\colon Y\to X$
. The functor
$p\colon Y\to X$
. The functor
![]() $f^*$
for
$f^*$
for
![]() $\mathcal {SH}$
is induced by that for
$\mathcal {SH}$
is induced by that for
![]() $\mathcal {H}_{\bullet }$
. This admits a right adjoint
$\mathcal {H}_{\bullet }$
. This admits a right adjoint
![]() $f_*$
, and this admits a left adjoint
$f_*$
, and this admits a left adjoint
![]() $f_{\sharp }$
if f is a finite covering. The functor
$f_{\sharp }$
if f is a finite covering. The functor
![]() $f_{\otimes }$
for
$f_{\otimes }$
for
![]() $\mathcal {SH}$
is the unique symmetric monoidal functor preserving sifted colimits such that the square
$\mathcal {SH}$
is the unique symmetric monoidal functor preserving sifted colimits such that the square

commutes. Furthermore, if f has connected fibers, then
![]() $f_{\otimes }$
preserves colimits.
$f_{\otimes }$
preserves colimits.
Proposition Appendix A.1.5. Suppose
![]() $X_1,\ldots ,X_n\in \mathrm {FinGpd}$
. Then there exists a canonical equivalence
$X_1,\ldots ,X_n\in \mathrm {FinGpd}$
. Then there exists a canonical equivalence
Proof. This is a consequence of [Reference Bachmann and Hoyois4, Lemma 9.6].
There is an alternative construction only inverting
![]() $S^1$
: By [Reference Bachmann and Hoyois4, Proposition 9.11], we have an equivalence
$S^1$
: By [Reference Bachmann and Hoyois4, Proposition 9.11], we have an equivalence
Proposition Appendix A.1.6. Suppose
![]() $X\in \mathrm {FinGpd}$
. Then the family
$X\in \mathrm {FinGpd}$
. Then the family
compactly generates
![]() $\mathcal {SH}(X)$
. In other words, the functor
$\mathcal {SH}(X)$
. In other words, the functor
![]() $\mathrm {Map}_{\mathcal {SH}(X)}(\Sigma ^n\Sigma ^{\infty } V_+,-)$
preserves filtered colimits for all
$\mathrm {Map}_{\mathcal {SH}(X)}(\Sigma ^n\Sigma ^{\infty } V_+,-)$
preserves filtered colimits for all
![]() $V\in \mathrm {Fin}_X$
and
$V\in \mathrm {Fin}_X$
and
![]() $n\in \mathbb {Z}$
, and the family of functors
$n\in \mathbb {Z}$
, and the family of functors
is conservative.
Proof. Using equation (A.5), we see that a map
![]() $\mathcal {G}\to \mathcal {F}$
in
$\mathcal {G}\to \mathcal {F}$
in
![]() $\mathcal {SH}(X)$
is an equivalence if and only if the induced map
$\mathcal {SH}(X)$
is an equivalence if and only if the induced map
![]() $\mathcal {G}(V)\to \mathcal {F}(V)$
is an equivalence for all
$\mathcal {G}(V)\to \mathcal {F}(V)$
is an equivalence for all
![]() $V\in \mathrm {Fin}_X$
. This is further equivalent to saying that the induced morphism
$V\in \mathrm {Fin}_X$
. This is further equivalent to saying that the induced morphism
![]() $\Omega ^{\infty } \Sigma ^{-n} \mathcal {G}(V)\to \Omega ^{\infty } \Sigma ^{-n} \mathcal {F}(V)$
is an equivalence for all
$\Omega ^{\infty } \Sigma ^{-n} \mathcal {G}(V)\to \Omega ^{\infty } \Sigma ^{-n} \mathcal {F}(V)$
is an equivalence for all
![]() $V\in \mathrm {Fin}_X$
and
$V\in \mathrm {Fin}_X$
and
![]() $n\in \mathbb {Z}$
. This proves that equation (A.6) is conservative. For the other claim, we reduce to the case when
$n\in \mathbb {Z}$
. This proves that equation (A.6) is conservative. For the other claim, we reduce to the case when
![]() $X=\mathrm {B} G$
using Proposition Appendix A.1.5 since every finite groupoid is equivalent to a finite disjoint union of classifying spaces. Then combine [Reference Lewis, May, Steinberger, McClure and Theory39, Lemma I.5.3] and [Reference Lurie42, Proposition 1.4.4.1(3)] to conclude. See also [Reference Hovey, Palmieri and Strickland32, Theorem 9.4.3].
$X=\mathrm {B} G$
using Proposition Appendix A.1.5 since every finite groupoid is equivalent to a finite disjoint union of classifying spaces. Then combine [Reference Lewis, May, Steinberger, McClure and Theory39, Lemma I.5.3] and [Reference Lurie42, Proposition 1.4.4.1(3)] to conclude. See also [Reference Hovey, Palmieri and Strickland32, Theorem 9.4.3].
Let
![]() $\mathrm {Fold}_X$
denote the full subcategory of
$\mathrm {Fold}_X$
denote the full subcategory of
![]() $\mathrm {Fin}_X$
consisting of the finite fold maps
$\mathrm {Fin}_X$
consisting of the finite fold maps
Proposition Appendix A.1.7. Let
![]() $f\colon X^{\amalg n} \to X$
be the n-fold map, where
$f\colon X^{\amalg n} \to X$
be the n-fold map, where
![]() $X\in \mathrm {FinGpd}$
and
$X\in \mathrm {FinGpd}$
and
![]() $n\geq 1$
is an integer. Then the composite
$n\geq 1$
is an integer. Then the composite
is the n-fold smash product.
Proof. One can show an analogous claim for
![]() $\mathcal {H}_{\bullet }$
as in [Reference Bachmann and Hoyois4, Theorem 3.3(6)]. To obtain the claim for
$\mathcal {H}_{\bullet }$
as in [Reference Bachmann and Hoyois4, Theorem 3.3(6)]. To obtain the claim for
![]() $\mathcal {SH}$
, use [Reference Bachmann and Hoyois4, Lemma 4.1].
$\mathcal {SH}$
, use [Reference Bachmann and Hoyois4, Lemma 4.1].
Definition Appendix A.1.8 ([Reference Bachmann and Hoyois4, Definition 9.14]).
Suppose
![]() $X\in \mathrm {FinGpd}$
. A normed X-spectrum is a section of
$X\in \mathrm {FinGpd}$
. A normed X-spectrum is a section of
![]() $\mathcal {SH}^{\otimes }$
over
$\mathcal {SH}^{\otimes }$
over
![]() $\mathrm {Span}(\mathrm {Fin}_X)$
that is co-Cartesian over the backward morphisms. Let
$\mathrm {Span}(\mathrm {Fin}_X)$
that is co-Cartesian over the backward morphisms. Let
![]() $\mathrm {NAlg}(\mathcal {SH}(X))$
denote the
$\mathrm {NAlg}(\mathcal {SH}(X))$
denote the
![]() $\infty $
-category of normed X-spectra.
$\infty $
-category of normed X-spectra.
Mapping X to
![]() $\mathrm {pt}$
yields an equivalence between
$\mathrm {pt}$
yields an equivalence between
![]() $\mathrm {Fold}_X$
and
$\mathrm {Fold}_X$
and
![]() $\mathrm {Fold}_{\mathrm {pt}}$
, and forgetting the map to
$\mathrm {Fold}_{\mathrm {pt}}$
, and forgetting the map to
![]() $\mathrm {pt} \ \mathrm {Fold}_{\mathrm {pt}}$
is obviously equivalent to the category of finite sets. By [Reference Bachmann and Hoyois4, Corollary C.2],
$\mathrm {pt} \ \mathrm {Fold}_{\mathrm {pt}}$
is obviously equivalent to the category of finite sets. By [Reference Bachmann and Hoyois4, Corollary C.2],
![]() $\mathrm {CAlg}(\mathcal {SH}(X))$
is equivalent to the
$\mathrm {CAlg}(\mathcal {SH}(X))$
is equivalent to the
![]() $\infty $
-category of sections of
$\infty $
-category of sections of
![]() $\mathcal {SH}^{\otimes }$
over
$\mathcal {SH}^{\otimes }$
over
![]() $\mathrm {Span}(\mathrm {Fold}_X)$
that is co-Cartesian over the backward morphisms. Hence, there is a forgetful functor
$\mathrm {Span}(\mathrm {Fold}_X)$
that is co-Cartesian over the backward morphisms. Hence, there is a forgetful functor
which is conservative and preserves colimit and limits as in [Reference Bachmann and Hoyois4, Proposition 7.6(3)]. This is an equivalence if
![]() $X=\mathrm {pt}$
since
$X=\mathrm {pt}$
since
![]() $\mathrm {Fold}_{\mathrm {pt}}\simeq \mathrm {Fin}_{\mathrm {pt}}$
. The forgetful functor
$\mathrm {Fold}_{\mathrm {pt}}\simeq \mathrm {Fin}_{\mathrm {pt}}$
. The forgetful functor
is conservative by [Reference Lurie42, Lemma 3.2.2.6]. It follows that the composite forgetful functor
![]() $\mathrm {NAlg}(\mathcal {SH}(X))\to \mathcal {SH}(X)$
is conservative too.
$\mathrm {NAlg}(\mathcal {SH}(X))\to \mathcal {SH}(X)$
is conservative too.
Suppose
![]() $X\in \mathrm {FinGpd}$
and
$X\in \mathrm {FinGpd}$
and
![]() $R\in \mathrm {CAlg}(\mathcal {SH}(X))$
. There is an induced commutative square
$R\in \mathrm {CAlg}(\mathcal {SH}(X))$
. There is an induced commutative square

The vertical functors are the forgetful functors, which is symmetric monoidal according to [Reference Lurie42, Example 3.2.4.4, Proposition 3.2.4.10]. Note that the symmetric monoidal structure on
![]() $\mathrm {CAlg}(-)$
is given by the coproduct. The monoidal product in
$\mathrm {CAlg}(-)$
is given by the coproduct. The monoidal product in
![]() $\mathcal {SH}(X)$
(resp.
$\mathcal {SH}(X)$
(resp.
![]() $\mathrm {Mod}_R$
) is denoted by
$\mathrm {Mod}_R$
) is denoted by
![]() $\wedge $
(resp.
$\wedge $
(resp.
![]() $\wedge _R$
). Then we have the induced monoidal products on
$\wedge _R$
). Then we have the induced monoidal products on
![]() $\mathrm {CAlg}(\mathcal {SH}(X))$
and
$\mathrm {CAlg}(\mathcal {SH}(X))$
and
![]() $\mathrm {CAlg}(\mathrm {Mod}_R)$
. There is an equivalence between
$\mathrm {CAlg}(\mathrm {Mod}_R)$
. There is an equivalence between
![]() $\mathrm {CAlg}(\mathrm {Mod}_R)$
and the
$\mathrm {CAlg}(\mathrm {Mod}_R)$
and the
![]() $\infty $
-category of R-algebras
$\infty $
-category of R-algebras
![]() $\mathrm {CAlg}(\mathcal {SH}(X))^{/R}$
by [Reference Lurie42, Corollary 3.4.1.7].
$\mathrm {CAlg}(\mathcal {SH}(X))^{/R}$
by [Reference Lurie42, Corollary 3.4.1.7].
The coproduct in
![]() $\mathrm {NAlg}(\mathcal {SH}(X))$
is also denoted by
$\mathrm {NAlg}(\mathcal {SH}(X))$
is also denoted by
![]() $\wedge $
. Since the forgetful functor
$\wedge $
. Since the forgetful functor
![]() $\mathrm {NAlg}(\mathcal {SH}(X))\to \mathrm {CAlg}(\mathcal {SH}(X))$
preserves colimits, the notation
$\mathrm {NAlg}(\mathcal {SH}(X))\to \mathrm {CAlg}(\mathcal {SH}(X))$
preserves colimits, the notation
![]() $\wedge $
on
$\wedge $
on
![]() $\mathrm {CAlg}(\mathcal {SH}(X))$
and
$\mathrm {CAlg}(\mathcal {SH}(X))$
and
![]() $\mathrm {NAlg}(\mathcal {SH}(X))$
is compatible.
$\mathrm {NAlg}(\mathcal {SH}(X))$
is compatible.
Proposition Appendix A.1.9. Let

be a Cartesian square in
![]() $\mathrm {FinGpd}$
such that f is a finite covering. For
$\mathrm {FinGpd}$
such that f is a finite covering. For
![]() $\mathcal {SH}$
, the natural transformation
$\mathcal {SH}$
, the natural transformation
given by the composite
is an equivalence.
Proof. As usual, Proposition Appendix A.1.6 allows us to reduce to showing that the induced map
![]() $f_{\sharp }^{\prime } g^{\prime *}\Sigma ^n\Sigma ^{\infty } W_+ \to g^*f_{\sharp } \Sigma ^n\Sigma ^{\infty } W_+$
is an equivalence for every
$f_{\sharp }^{\prime } g^{\prime *}\Sigma ^n\Sigma ^{\infty } W_+ \to g^*f_{\sharp } \Sigma ^n\Sigma ^{\infty } W_+$
is an equivalence for every
![]() $W\in \mathrm {Fin}_Y$
and integer n. This follows from the fact that the composite of the induced morphisms
$W\in \mathrm {Fin}_Y$
and integer n. This follows from the fact that the composite of the induced morphisms
is an isomorphism.
Proposition Appendix A.1.10. Let
![]() $f\colon Y\to X$
be a finite covering. Then for
$f\colon Y\to X$
be a finite covering. Then for
![]() $\mathcal {F}\in \mathcal {SH}(Y)$
and
$\mathcal {F}\in \mathcal {SH}(Y)$
and
![]() $\mathcal {G}\in \mathcal {SH}(X)$
, there exists a canonical equivalence
$\mathcal {G}\in \mathcal {SH}(X)$
, there exists a canonical equivalence
Proof. As usual, Proposition Appendix A.1.6 allows us to reduce to the case when
![]() $\mathcal {F}=\Sigma ^m\Sigma ^{\infty } V_+$
and
$\mathcal {F}=\Sigma ^m\Sigma ^{\infty } V_+$
and
![]() $\mathcal {G}=\Sigma ^n\Sigma ^{\infty } W_+$
for some
$\mathcal {G}=\Sigma ^n\Sigma ^{\infty } W_+$
for some
![]() $V\in \mathrm {Fin}_Y$
,
$V\in \mathrm {Fin}_Y$
,
![]() $W\in \mathrm {Fin}_X$
and
$W\in \mathrm {Fin}_X$
and
![]() $m,n\in \mathbb {Z}$
. In this case, the canonical isomorphism
$m,n\in \mathbb {Z}$
. In this case, the canonical isomorphism
gives the desired equivalence.
Let
![]() $f\colon Y\to X$
be a morphism in
$f\colon Y\to X$
be a morphism in
![]() $\mathrm {FinGpd}$
. The formulation equation (A.3) tells that the functor
$\mathrm {FinGpd}$
. The formulation equation (A.3) tells that the functor
![]() $f^*$
is symmetric monoidal. Hence, we obtain an induced adjoint pair
$f^*$
is symmetric monoidal. Hence, we obtain an induced adjoint pair
by [Reference Lurie42, Remark 7.3.2.13]. The formulation of these functors provided in [Reference Lurie42, Proposition 7.3.2.5] shows that the two squares in

commute, where the vertical functors are the forgetful functors.
If f has connected fibers, then we noted that
![]() $f_{\otimes }$
preserves colimits. Hence, we similarly obtain a functor
$f_{\otimes }$
preserves colimits. Hence, we similarly obtain a functor
and a commutative square

The following should be compared with equation (A.16).
Proposition Appendix A.1.11. Let
![]() $f\colon Y\to X$
be a finite covering in
$f\colon Y\to X$
be a finite covering in
![]() $\mathrm {FinGpd}$
. Then there is an induced adjunction
$\mathrm {FinGpd}$
. Then there is an induced adjunction
Furthermore, the two squares in

commute, where the vertical functors are the forgetful functors.
Proof. Apply [Reference Bachmann and Hoyois4, Theorem 8.5] to the case when
![]() $\mathcal {C}:=\mathrm {FinGpd}$
,
$\mathcal {C}:=\mathrm {FinGpd}$
,
![]() $\mathcal {A}:=\mathcal {SH}^{\otimes }$
and
$\mathcal {A}:=\mathcal {SH}^{\otimes }$
and
![]() $\mathrm {right}$
(resp.
$\mathrm {right}$
(resp.
![]() $\mathrm {left}$
) is the class of all morphisms (finite coverings) in
$\mathrm {left}$
) is the class of all morphisms (finite coverings) in
![]() $\mathrm {FinGpd}$
. Then
$\mathrm {FinGpd}$
. Then
![]() $\mathrm {Sect}(\mathcal {A}_X)$
in the reference is precisely
$\mathrm {Sect}(\mathcal {A}_X)$
in the reference is precisely
![]() $\mathrm {NAlg}(\mathcal {SH}(X))$
for
$\mathrm {NAlg}(\mathcal {SH}(X))$
for
![]() $X\in \mathrm {FinGpd}$
. Hence, as observed in [Reference Bachmann and Hoyois4, Remark 8.6], we have the desired adjunction such that the two squares in equation (A.13) commutes.
$X\in \mathrm {FinGpd}$
. Hence, as observed in [Reference Bachmann and Hoyois4, Remark 8.6], we have the desired adjunction such that the two squares in equation (A.13) commutes.
Proposition Appendix A.1.12. Let
![]() $f\colon Y\to X$
be a finite covering in
$f\colon Y\to X$
be a finite covering in
![]() $\mathrm {FinGpd}$
. Then there is an induced adjunction
$\mathrm {FinGpd}$
. Then there is an induced adjunction
Furthermore, the two squares in

commute, where the vertical functors are the forgetful functors.
Proof. Let us imitate the proof of [Reference Bachmann and Hoyois4, Theorem 8.2]. By [Reference Bachmann and Hoyois4, Corollary C.21(2)], there is an induced adjunction
Let
![]() $\mathcal {SH}^{\otimes }\vert \mathrm {Span}(\mathrm {Fin}_X)$
be the restriction of
$\mathcal {SH}^{\otimes }\vert \mathrm {Span}(\mathrm {Fin}_X)$
be the restriction of
![]() $\mathcal {SH}^{\otimes }$
to
$\mathcal {SH}^{\otimes }$
to
![]() $\mathrm {Span}(\mathrm {Fin}_X)$
. For every
$\mathrm {Span}(\mathrm {Fin}_X)$
. For every
![]() $V\in \mathrm {Span}(\mathrm {Fin}_X)$
, let
$V\in \mathrm {Span}(\mathrm {Fin}_X)$
, let
![]() $f_V\colon V\times _X Y\to V$
be the projection. The functor
$f_V\colon V\times _X Y\to V$
be the projection. The functor
![]() $f_V^*\colon \mathcal {SH}(V)\to \mathcal {SH}(V\times _X Y)$
admits the right adjoint
$f_V^*\colon \mathcal {SH}(V)\to \mathcal {SH}(V\times _X Y)$
admits the right adjoint
![]() $f_{V*}$
. Apply [Reference Bachmann and Hoyois4, Proposition 8.16] to the co-Cartesian fibration
$f_{V*}$
. Apply [Reference Bachmann and Hoyois4, Proposition 8.16] to the co-Cartesian fibration
![]() $\mathcal {SH}^{\otimes }\vert \mathrm {Span}(\mathrm {Fin}_X)$
to obtain the desired adjunction.
$\mathcal {SH}^{\otimes }\vert \mathrm {Span}(\mathrm {Fin}_X)$
to obtain the desired adjunction.
Let us review the descriptions of
![]() $f^*$
and
$f^*$
and
![]() $f_*$
for
$f_*$
for
![]() $\mathrm {NAlg}$
in this reference. The functor
$\mathrm {NAlg}$
in this reference. The functor
![]() $f^*$
for
$f^*$
for
![]() $\mathrm {NAlg}$
used here is the same as the functor
$\mathrm {NAlg}$
used here is the same as the functor
![]() $f^*$
for
$f^*$
for
![]() $\mathrm {NAlg}$
in Proposition Appendix A.1.11. Suppose
$\mathrm {NAlg}$
in Proposition Appendix A.1.11. Suppose
![]() $B\in \mathrm {NAlg}(\mathcal {SH}(Y))$
. For
$B\in \mathrm {NAlg}(\mathcal {SH}(Y))$
. For
![]() $V\in \mathrm {Span}(\mathrm {Fin}_X)$
, the section
$V\in \mathrm {Span}(\mathrm {Fin}_X)$
, the section
![]() $(f_*B)(V)$
is given by
$(f_*B)(V)$
is given by
![]() $f_{V*}(B(V\times _X Y))$
. In particular, the section
$f_{V*}(B(V\times _X Y))$
. In particular, the section
![]() $(f_*B)(X)$
is given by
$(f_*B)(X)$
is given by
![]() $f_*(B(X))$
. Hence, the two squares in equation (A.14) commute.
$f_*(B(X))$
. Hence, the two squares in equation (A.14) commute.
For abbreviation, we set
This notation is further justified by Remark Appendix A.2.3.
A.2 Equivariant orthogonal spectra
The purpose of this section is to review equivariant homotopy theory using model categories. Our references for that are [Reference Greenlees and May23], [Reference Mandell and May44], [Reference Hill, Hopkins and Ravenel29] and [Reference Schwede53]. We will also review the comparison between
![]() $\infty $
-categorical and model categorical constructions of equivariant spectra. Consequently, we may apply certain known constructions and results for equivariant orthogonal spectra to
$\infty $
-categorical and model categorical constructions of equivariant spectra. Consequently, we may apply certain known constructions and results for equivariant orthogonal spectra to
![]() $\infty $
-categories as discussed in the previous subsection.
$\infty $
-categories as discussed in the previous subsection.
Let
![]() $\mathrm {B} G$
denote the associated finite groupoid. In this subsection, we are interested in the obvious morphisms
$\mathrm {B} G$
denote the associated finite groupoid. In this subsection, we are interested in the obvious morphisms
where
![]() $H\to G$
is an inclusion.
$H\to G$
is an inclusion.
Definition Appendix A.2.1. Let
![]() $\mathrm {Sp}^O$
denote the category of orthogonal spectra. For a finite group G, let
$\mathrm {Sp}^O$
denote the category of orthogonal spectra. For a finite group G, let
![]() $\mathrm {Sp}^O_G$
denote the category of orthogonal G-spectra. Recall that an orthogonal G-spectrum is an orthogonal spectrum with a G-action. A morphism of orthogonal G-spectra is a morphism of underlying orthogonal spectra that is compatible with the G-actions.
$\mathrm {Sp}^O_G$
denote the category of orthogonal G-spectra. Recall that an orthogonal G-spectrum is an orthogonal spectrum with a G-action. A morphism of orthogonal G-spectra is a morphism of underlying orthogonal spectra that is compatible with the G-actions.
The definition of orthogonal G-spectra in [Reference Hill, Hopkins and Ravenel29] is different from the above one, but the two categories are equivalent. See [Reference Schwede53, Remark 2.7] for the details.
Definition Appendix A.2.2. The category
![]() $\mathrm {Sp}^O_G$
admits a symmetric monoidal model structure; see [Reference Hill, Hopkins and Ravenel29, Propositions B.63, B.76]. We denote the (model) category of commutative monoids in
$\mathrm {Sp}^O_G$
admits a symmetric monoidal model structure; see [Reference Hill, Hopkins and Ravenel29, Propositions B.63, B.76]. We denote the (model) category of commutative monoids in
![]() $\mathrm {Sp}^O$
by
$\mathrm {Sp}^O$
by
![]() $\mathrm {CAlg}^O$
. According to [Reference Hill, Hopkins and Ravenel29], we sometimes denote it also by
$\mathrm {CAlg}^O$
. According to [Reference Hill, Hopkins and Ravenel29], we sometimes denote it also by
![]() $\mathbf {Comm}$
, and the (model) category of commutative monoids in
$\mathbf {Comm}$
, and the (model) category of commutative monoids in
![]() $\mathrm {Sp}^O_G$
by
$\mathrm {Sp}^O_G$
by
![]() $\mathbf {\mathbf {Comm}_G}$
. We refer to [Reference Hill, Hopkins and Ravenel29, section A.1.2] for the details. According to [Reference Hill, Hopkins and Ravenel29, Proposition B.129],
$\mathbf {\mathbf {Comm}_G}$
. We refer to [Reference Hill, Hopkins and Ravenel29, section A.1.2] for the details. According to [Reference Hill, Hopkins and Ravenel29, Proposition B.129],
![]() $\mathbf {Comm}_G$
has a nice model structure. A morphism in
$\mathbf {Comm}_G$
has a nice model structure. A morphism in
![]() $\mathbf {Comm}_G$
is a weak equivalence (resp. fibration) precisely when its underlying morphism in
$\mathbf {Comm}_G$
is a weak equivalence (resp. fibration) precisely when its underlying morphism in
![]() $\mathrm {Sp}^O_G$
is a weak equivalence (resp. fibration). The (underived) coproduct in
$\mathrm {Sp}^O_G$
is a weak equivalence (resp. fibration). The (underived) coproduct in
![]() $\mathbf {Comm}_G$
is denoted by
$\mathbf {Comm}_G$
is denoted by
![]() $\wedge $
.
$\wedge $
.
Remark Appendix A.2.3. As observed in the preceding paragraphs of [Reference Bachmann and Hoyois4, Lemma 9.6],
![]() $\mathrm {Sp}_G$
is equivalent to the underlying
$\mathrm {Sp}_G$
is equivalent to the underlying
![]() $\infty $
-category of the model category of symmetric G-spectra. This is equivalent to the underlying
$\infty $
-category of the model category of symmetric G-spectra. This is equivalent to the underlying
![]() $\infty $
-category of
$\infty $
-category of
![]() $\mathrm {Sp}^O_G$
by [Reference Mandell43]. See also [Reference Bachmann and Hoyois4, Remark 9.12] for another
$\mathrm {Sp}^O_G$
by [Reference Mandell43]. See also [Reference Bachmann and Hoyois4, Remark 9.12] for another
![]() $\infty $
-description. Furthermore, as observed in [Reference Bachmann and Hoyois4, after Definition 9.14],
$\infty $
-description. Furthermore, as observed in [Reference Bachmann and Hoyois4, after Definition 9.14],
![]() $\mathrm {NAlg}_G$
is equivalent to the underlying
$\mathrm {NAlg}_G$
is equivalent to the underlying
![]() $\infty $
-category of the model category of G-
$\infty $
-category of the model category of G-
![]() $\mathbb {E}_{\infty }$
-rings, which is equivalent to the underlying
$\mathbb {E}_{\infty }$
-rings, which is equivalent to the underlying
![]() $\infty $
-category of
$\infty $
-category of
![]() $\mathbf {Comm}_G$
. We refer to [Reference Gutiérrez and White24] for a comparison of different models, rectification results and further references.
$\mathbf {Comm}_G$
. We refer to [Reference Gutiérrez and White24] for a comparison of different models, rectification results and further references.
Construction Appendix A.2.4. Let H be a subgroup of G, with the inclusion map
![]() $H\to G$
. (For
$H\to G$
. (For
![]() $H=\mathrm {pt}$
, compare Example Appendix A.1.2.) Let us review several functors from [Reference Hill, Hopkins and Ravenel29, sections 2.2.3, 2.5.1]. The norm functor
$H=\mathrm {pt}$
, compare Example Appendix A.1.2.) Let us review several functors from [Reference Hill, Hopkins and Ravenel29, sections 2.2.3, 2.5.1]. The norm functor
sends
![]() $Y\in \mathrm {Sp}^O_H$
to
$Y\in \mathrm {Sp}^O_H$
to
![]() $\bigwedge _{i\in G/H} Y$
with a suitable G-action. If
$\bigwedge _{i\in G/H} Y$
with a suitable G-action. If
![]() $H=\mathrm {pt}$
, we often simply write
$H=\mathrm {pt}$
, we often simply write
![]() $N^G$
.
$N^G$
.
The restriction functor
sends
![]() $X\in \mathrm {Sp}^O_G$
to X, and the action is the restriction of the G-action to H. Its left adjoint
$X\in \mathrm {Sp}^O_G$
to X, and the action is the restriction of the G-action to H. Its left adjoint
![]() $i_{\sharp }$
and right adjoint
$i_{\sharp }$
and right adjoint
![]() $i_*$
send
$i_*$
send
![]() $X\in \mathrm {Sp}^O_H$
to
$X\in \mathrm {Sp}^O_H$
to
 $$ \begin{align} \bigvee_{i\in G/H} X_i \text{ and } \prod_{i\in G/H} X_i \end{align} $$
$$ \begin{align} \bigvee_{i\in G/H} X_i \text{ and } \prod_{i\in G/H} X_i \end{align} $$
respectively, where
![]() $X_i:=H_i\wedge _H X$
and
$X_i:=H_i\wedge _H X$
and
![]() $H_i\subset G$
is the coset indexed by G. According to [Reference Hill, Hopkins and Ravenel29, Proposition B.72],
$H_i\subset G$
is the coset indexed by G. According to [Reference Hill, Hopkins and Ravenel29, Proposition B.72],
![]() $i^*$
is a left and right Quillen functor. Hence, we have Quillen adjunctions
$i^*$
is a left and right Quillen functor. Hence, we have Quillen adjunctions
We also have the functor
imposing the trivial G-action. The fixed point functor
sends an orthogonal G-spectrum
![]() $(X_0,X_1,\ldots )$
to
$(X_0,X_1,\ldots )$
to
![]() $(X_0^G,X_1^G,\ldots )$
. There is a Quillen adjunction
$(X_0^G,X_1^G,\ldots )$
. There is a Quillen adjunction
Construction Appendix A.2.5. For the definition of the geometric fixed point functor
we refer to [Reference Hill, Hopkins and Ravenel29, section B.10.1]. There is yet another functor
in [Reference Hill, Hopkins and Ravenel29, Definition B.190], which is called the monoidal geometric fixed point functor. This is lax monoidal and preserves cofibrations and acyclic cofibrations; see [Reference Hill, Hopkins and Ravenel29, sections B.10.3, B.10.4].
According to [Reference Hill, Hopkins and Ravenel29, Proposition B.201], there is a zig-zag of weak equivalences between
![]() $\Phi ^G(X)$
and
$\Phi ^G(X)$
and
![]() $\Phi _M^G(X)$
whenever
$\Phi _M^G(X)$
whenever
![]() $X\in \mathrm {Sp}^O_G$
is cofibrant.
$X\in \mathrm {Sp}^O_G$
is cofibrant.
Remark Appendix A.2.6. The functor
![]() $i^*\colon \mathrm {Sp}^O_H \to \mathrm {Sp}^O_G$
is a model for the functor of
$i^*\colon \mathrm {Sp}^O_H \to \mathrm {Sp}^O_G$
is a model for the functor of
![]() $\infty $
-categories
$\infty $
-categories
![]() $i^*\colon \mathrm {Sp}_H \to \mathrm {Sp}_G$
since their values on
$i^*\colon \mathrm {Sp}_H \to \mathrm {Sp}_G$
since their values on
![]() $\Sigma ^n\Sigma ^{\infty } X_+$
are equivalent for all
$\Sigma ^n\Sigma ^{\infty } X_+$
are equivalent for all
![]() $X\in \mathrm {Fin}_H$
and integers n. Likewise, the functor
$X\in \mathrm {Fin}_H$
and integers n. Likewise, the functor
![]() $\iota \colon \mathrm {Sp}^O\to \mathrm {Sp}^O_G$
is a model for the functor
$\iota \colon \mathrm {Sp}^O\to \mathrm {Sp}^O_G$
is a model for the functor
![]() $p^*\colon \mathrm {Sp}\to \mathrm {Sp}_G$
, where
$p^*\colon \mathrm {Sp}\to \mathrm {Sp}_G$
, where
![]() $p\colon \mathrm {B} G \to \mathrm {pt}$
. It follows by the uniqueness of
$p\colon \mathrm {B} G \to \mathrm {pt}$
. It follows by the uniqueness of
![]() $\infty $
-adjoints that the fixed point functor
$\infty $
-adjoints that the fixed point functor
![]() $(-)^G\colon \mathrm {Sp}^O_G \to \mathrm {Sp}^O$
is a model for the functor
$(-)^G\colon \mathrm {Sp}^O_G \to \mathrm {Sp}^O$
is a model for the functor
![]() $p_*\colon \mathrm {Sp}^O_G\to \mathrm {Sp}^O$
. We have similar comparison results for
$p_*\colon \mathrm {Sp}^O_G\to \mathrm {Sp}^O$
. We have similar comparison results for
![]() $i_{\sharp }$
and
$i_{\sharp }$
and
![]() $i_*$
.
$i_*$
.
According to [Reference Bachmann and Hoyois4, Remark 9.10], the norm functor
![]() $N^G_H\colon \mathrm {Sp}^O_H\to \mathrm {Sp}^O_G$
is a model for the functor
$N^G_H\colon \mathrm {Sp}^O_H\to \mathrm {Sp}^O_G$
is a model for the functor
![]() $i_{\otimes }\colon \mathrm {Sp}_H \to \mathrm {Sp}_G$
, and the geometric fixed point functor
$i_{\otimes }\colon \mathrm {Sp}_H \to \mathrm {Sp}_G$
, and the geometric fixed point functor
![]() $\Phi ^G\colon \mathrm {Sp}^O_G\to \mathrm {Sp}^O$
is a model for the functor
$\Phi ^G\colon \mathrm {Sp}^O_G\to \mathrm {Sp}^O$
is a model for the functor
![]() $p_{\otimes }\colon \mathrm {Sp}_G\to \mathrm {Sp}$
. It follows that
$p_{\otimes }\colon \mathrm {Sp}_G\to \mathrm {Sp}$
. It follows that
![]() $\Phi _M^G$
is a model for
$\Phi _M^G$
is a model for
![]() $p_{\otimes }$
too.
$p_{\otimes }$
too.
The functors
![]() $N_H^G\colon \mathrm {Sp}^O_H \to \mathrm {Sp}^O_G$
and
$N_H^G\colon \mathrm {Sp}^O_H \to \mathrm {Sp}^O_G$
and
![]() $i^*\colon \mathrm {Sp}^O_H\to \mathrm {Sp}^O_G$
are symmetric monoidal. By [Reference Hill, Hopkins and Ravenel29, Proposition 2.27], they induce a Quillen adjunction
$i^*\colon \mathrm {Sp}^O_H\to \mathrm {Sp}^O_G$
are symmetric monoidal. By [Reference Hill, Hopkins and Ravenel29, Proposition 2.27], they induce a Quillen adjunction
In short, comparing the adjunctions between
![]() $\mathbf {Comm}_G$
with those for the underlying spectra,
$\mathbf {Comm}_G$
with those for the underlying spectra,
![]() $N_H^G$
already exists for spectra, but only becomes a left adjoint to
$N_H^G$
already exists for spectra, but only becomes a left adjoint to
![]() $i^*$
in
$i^*$
in
![]() $\mathbf {Comm}_G$
, replacing
$\mathbf {Comm}_G$
, replacing
![]() $i_{\sharp }$
.
$i_{\sharp }$
.
Compare the diagram in [Reference Hill, Hopkins and Ravenel29, Proposition A.56] with equation (A.12) and use the conservativity of the forgetful functor
![]() $\mathrm {NAlg}_G\to \mathrm {Sp}_G$
to show that
$\mathrm {NAlg}_G\to \mathrm {Sp}_G$
to show that
![]() $N_H^G\colon \mathbf {Comm}_H \to \mathbf {Comm}_G$
is a model for the functor
$N_H^G\colon \mathbf {Comm}_H \to \mathbf {Comm}_G$
is a model for the functor
![]() $i_{\otimes } \colon \mathrm {NAlg}_H\to \mathrm {NAlg}_G$
. Then
$i_{\otimes } \colon \mathrm {NAlg}_H\to \mathrm {NAlg}_G$
. Then
![]() $i^*\colon \mathbf {Comm}_G\to \mathbf {Comm}_H$
is a model for the functor
$i^*\colon \mathbf {Comm}_G\to \mathbf {Comm}_H$
is a model for the functor
![]() $i^*\colon \mathrm {NAlg}_G \to \mathrm {NAlg}_H$
by adjunction.
$i^*\colon \mathrm {NAlg}_G \to \mathrm {NAlg}_H$
by adjunction.
Proposition Appendix A.2.7. We have the following equivalences of functors between
![]() $\infty $
-categories
$\infty $
-categories
![]() $\mathrm {Sp}_G$
for appropriate G:
$\mathrm {Sp}_G$
for appropriate G:
-
(1)
 $p_{\otimes } i_{\otimes } \simeq \mathrm {id}$
if
$p_{\otimes } i_{\otimes } \simeq \mathrm {id}$
if
 $H=e$
,
$H=e$
, -
(2)
 $i^*p^*\simeq \mathrm {id}$
if
$i^*p^*\simeq \mathrm {id}$
if
 $H=e$
,
$H=e$
, -
(3)
 $i_{\sharp }\xrightarrow {\simeq } i_*$
,
$i_{\sharp }\xrightarrow {\simeq } i_*$
, -
(4)
 $\mathrm {id} \xrightarrow {\simeq } p_{\otimes } p^*$
,
$\mathrm {id} \xrightarrow {\simeq } p_{\otimes } p^*$
, -
(5)
 $p_{\otimes } i_{\sharp } \simeq 0$
if
$p_{\otimes } i_{\sharp } \simeq 0$
if
 $G\neq e$
,
$G\neq e$
, -
(6)
 $i^*i_{\otimes }\simeq (-)^{\wedge [G:H]}$
,
$i^*i_{\otimes }\simeq (-)^{\wedge [G:H]}$
, -
(7)
 $i^*i_{\sharp }\simeq (-)^{\oplus [G:H]}$
.
$i^*i_{\sharp }\simeq (-)^{\oplus [G:H]}$
.
Proof. The first two follow from
![]() $pi=\mathrm {id}$
. The next three follow from [Reference Hill, Hopkins and Ravenel29, Propositions B.56, B.182, B.192]. For (6), consider the Cartesian square
$pi=\mathrm {id}$
. The next three follow from [Reference Hill, Hopkins and Ravenel29, Propositions B.56, B.182, B.192]. For (6), consider the Cartesian square

where q is the
![]() $\lvert G/H \rvert $
-fold map. If
$\lvert G/H \rvert $
-fold map. If
![]() $\bar {i}$
and
$\bar {i}$
and
![]() $\bar {q}$
denote the forward morphisms in
$\bar {q}$
denote the forward morphisms in
![]() $\mathrm {Span}(\mathrm {FinGpd})$
associated with i and q, then
$\mathrm {Span}(\mathrm {FinGpd})$
associated with i and q, then
![]() $\bar {i}i\simeq q\bar {q}$
. Hence, we have an equivalence
$\bar {i}i\simeq q\bar {q}$
. Hence, we have an equivalence
![]() $i^*i_{\otimes } \simeq q_{\otimes } q^*$
. Together with Proposition Appendix A.1.7, we obtain the desired equivalence. For (7), Proposition Appendix A.1.9 gives an equivalence
$i^*i_{\otimes } \simeq q_{\otimes } q^*$
. Together with Proposition Appendix A.1.7, we obtain the desired equivalence. For (7), Proposition Appendix A.1.9 gives an equivalence
![]() $i^*i_{\sharp }\simeq q_{\sharp } q^*$
. The functor
$i^*i_{\sharp }\simeq q_{\sharp } q^*$
. The functor
![]() $q^*$
can be identified with the diagonal functor
$q^*$
can be identified with the diagonal functor
![]() $\mathrm {Sp}_H \to (\mathrm {Sp}_H)^{\times G/H}$
, and the functor
$\mathrm {Sp}_H \to (\mathrm {Sp}_H)^{\times G/H}$
, and the functor
![]() $q_{\sharp }$
can be identified with the
$q_{\sharp }$
can be identified with the
![]() $[G:H]$
-fold direct sum
$[G:H]$
-fold direct sum
![]() $(\mathrm {Sp}_H)^{\times G/H}\to \mathrm {Sp}_H$
. Use these facts to conclude.
$(\mathrm {Sp}_H)^{\times G/H}\to \mathrm {Sp}_H$
. Use these facts to conclude.
Remark Appendix A.2.8. Recall that the forgetful functors
![]() $\mathrm {CAlg}_G\to \mathrm {Sp}_G$
and
$\mathrm {CAlg}_G\to \mathrm {Sp}_G$
and
![]() $\mathrm {NAlg}_G\to \mathrm {Sp}_G$
are conservative. Together with equations (A.10) and (A.12), we see that Proposition Appendix A.2.7(2),(4) holds for
$\mathrm {NAlg}_G\to \mathrm {Sp}_G$
are conservative. Together with equations (A.10) and (A.12), we see that Proposition Appendix A.2.7(2),(4) holds for
![]() $\mathrm {CAlg}_G$
for appropriate G. Similarly, together with equation (A.13), we see that Proposition Appendix A.2.7(2),(6) holds for
$\mathrm {CAlg}_G$
for appropriate G. Similarly, together with equation (A.13), we see that Proposition Appendix A.2.7(2),(6) holds for
![]() $\mathrm {NAlg}_G$
for appropriate G.
$\mathrm {NAlg}_G$
for appropriate G.
Lemma Appendix A.2.9. Suppose
![]() $R\in \mathrm {CAlg}$
,
$R\in \mathrm {CAlg}$
,
![]() $M\in \mathrm {Mod}_R$
and
$M\in \mathrm {Mod}_R$
and
![]() $L\in \mathrm {Mod}_{p^* R}$
. If M and R are connective, then there exists a canonical equivalence of R-modules
$L\in \mathrm {Mod}_{p^* R}$
. If M and R are connective, then there exists a canonical equivalence of R-modules
Proof. We have maps
where the second map is induced by the counit map
![]() $p^*p_*L\to L$
. By adjunction, we obtain
$p^*p_*L\to L$
. By adjunction, we obtain
![]() $M\wedge _R p_*L\to p_*(p^* M\wedge _{p^*R}L)$
. We only need to show that this is an equivalence in
$M\wedge _R p_*L\to p_*(p^* M\wedge _{p^*R}L)$
. We only need to show that this is an equivalence in
![]() $\mathrm {Sp}$
after forgetting the module structures.
$\mathrm {Sp}$
after forgetting the module structures.
Let
![]() $\mathcal {F}$
be the class of R-modules M such that this map is an equivalence. The functors
$\mathcal {F}$
be the class of R-modules M such that this map is an equivalence. The functors
![]() $p^*$
,
$p^*$
,
![]() $\wedge _R p_*L$
and
$\wedge _R p_*L$
and
![]() $\wedge _{p^*R} L$
preserve colimits. As explained after [Reference Mathew, Naumann and Noel45, Remark 6.8], the functor
$\wedge _{p^*R} L$
preserve colimits. As explained after [Reference Mathew, Naumann and Noel45, Remark 6.8], the functor
![]() $p_*$
preserves colimits too. It follows that
$p_*$
preserves colimits too. It follows that
![]() $\mathcal {F}$
is closed under colimits. Furthermore,
$\mathcal {F}$
is closed under colimits. Furthermore,
![]() $\mathcal {F}$
is closed under shifts. Since
$\mathcal {F}$
is closed under shifts. Since
![]() $\mathcal {F}$
contains R,
$\mathcal {F}$
contains R,
![]() $\mathcal {F}$
contains all connective R-modules by [Reference Lurie42, Proposition 7.1.1.13].
$\mathcal {F}$
contains all connective R-modules by [Reference Lurie42, Proposition 7.1.1.13].
A.3 Mackey functors
Definition Appendix A.3.1. Recall from [Reference Hill, Hopkins and Ravenel30, Definition 8.2.5] that a Mackey functor for G (or simply Mackey functor) is a presheaf M on
![]() $\mathrm {Span}(\mathrm {Fin}_{\mathrm {B} G})$
of abelian groups that transforms finite coproducts into finite products. (This is easily seen to be equivalent to more classical definitions as, e.g., recalled in [Reference Hill, Hopkins and Ravenel29, Definition 3.1].) For a forward (resp. backward) morphism f in
$\mathrm {Span}(\mathrm {Fin}_{\mathrm {B} G})$
of abelian groups that transforms finite coproducts into finite products. (This is easily seen to be equivalent to more classical definitions as, e.g., recalled in [Reference Hill, Hopkins and Ravenel29, Definition 3.1].) For a forward (resp. backward) morphism f in
![]() $\mathrm {Span}(\mathrm {Fin}_{\mathrm {B} G})$
,
$\mathrm {Span}(\mathrm {Fin}_{\mathrm {B} G})$
,
![]() $M(f)$
is called a restriction map (resp. transfer map). Let
$M(f)$
is called a restriction map (resp. transfer map). Let
![]() $\mathrm {Mack}_G$
denote the category of Mackey functors for G. We include the explicit description of Mackey functors for
$\mathrm {Mack}_G$
denote the category of Mackey functors for G. We include the explicit description of Mackey functors for
![]() ${\mathbb {Z}/2}$
in Example 2.2.1.
${\mathbb {Z}/2}$
in Example 2.2.1.
For all
![]() $X\in \mathrm {Sp}_G$
,
$X\in \mathrm {Sp}_G$
,
![]() $M\in \mathrm {Fin}_{\mathrm {B} G}$
and integers n, we set
$M\in \mathrm {Fin}_{\mathrm {B} G}$
and integers n, we set
where the isomorphism comes from [Reference Hill, Hopkins and Ravenel29, Example 2.6]. The first (resp. second) formulation is contravariant (resp. covariant) in M, and these two can be combined to produce the equivariant homotopy group functor
We refer to [Reference Hill, Hopkins and Ravenel29, section 3.1] for the details. For
![]() $X\in \mathrm {Sp}_G$
and an integer n, we say that X is n-connected if
$X\in \mathrm {Sp}_G$
and an integer n, we say that X is n-connected if
![]() $\underline {\pi }_k(X)=0$
for all integers
$\underline {\pi }_k(X)=0$
for all integers
![]() $k\leq n$
.
$k\leq n$
.
Proposition Appendix A.3.2. For every integer n,
![]() $\underline {\pi }_n$
preserves products and filtered colimits.
$\underline {\pi }_n$
preserves products and filtered colimits.
Proof. The claim for products follows from the first formulation in equation (A.17). By Proposition Appendix A.1.6,
![]() $\Sigma ^n \Sigma ^{\infty } M_+$
is compact, that is,
$\Sigma ^n \Sigma ^{\infty } M_+$
is compact, that is,
![]() $\mathrm {Map}_{\mathrm {Sp}_G}(\Sigma ^n\Sigma ^{\infty } M_+,-)$
preserves filtered colimits. This immediately implies the claim.
$\mathrm {Map}_{\mathrm {Sp}_G}(\Sigma ^n\Sigma ^{\infty } M_+,-)$
preserves filtered colimits. This immediately implies the claim.
Now, suppose
![]() $M\in \mathrm {Mack}_{G}$
. According to [Reference Greenlees and May23, Theorem 5.3], one can associate an equivariant Eilenberg–MacLane spectrum
$M\in \mathrm {Mack}_{G}$
. According to [Reference Greenlees and May23, Theorem 5.3], one can associate an equivariant Eilenberg–MacLane spectrum
![]() $\mathrm {H} M\in \mathrm {Sp}^O_{G}$
, which satisfies
$\mathrm {H} M\in \mathrm {Sp}^O_{G}$
, which satisfies
 $$\begin{align*}\underline{\pi}_n(\mathrm{H} M) \cong \left\{ \begin{array}{ll} M & \text{if }n=0, \\ 0 & \text{if }n\neq 0. \end{array} \right. \end{align*}$$
$$\begin{align*}\underline{\pi}_n(\mathrm{H} M) \cong \left\{ \begin{array}{ll} M & \text{if }n=0, \\ 0 & \text{if }n\neq 0. \end{array} \right. \end{align*}$$
Furthermore,
![]() $\mathrm {H} M$
is unique up to an isomorphism in the homotopy category
$\mathrm {H} M$
is unique up to an isomorphism in the homotopy category
![]() $\mathrm {Ho}(\mathrm {Sp}^O_{G})\simeq \mathrm {Ho}(\mathrm {Sp}_G)$
, and there is a canonical isomorphism
$\mathrm {Ho}(\mathrm {Sp}^O_{G})\simeq \mathrm {Ho}(\mathrm {Sp}_G)$
, and there is a canonical isomorphism
for all
![]() $M,L\in \mathrm {Mack}_{G}$
. It follows that we have a functor
$M,L\in \mathrm {Mack}_{G}$
. It follows that we have a functor
Definition Appendix A.3.3. Let n be an integer. Let
![]() $(\mathrm {Sp}_G)_{\geq n}$
(resp.
$(\mathrm {Sp}_G)_{\geq n}$
(resp.
![]() $(\mathrm {Sp}_G)_{\leq n}$
) denote the full subcategory of
$(\mathrm {Sp}_G)_{\leq n}$
) denote the full subcategory of
![]() $\mathrm {Sp}_G$
spanned by
$\mathrm {Sp}_G$
spanned by
![]() $X\in \mathrm {Sp}_G$
such that
$X\in \mathrm {Sp}_G$
such that
![]() $\underline {\pi }_k(X)=0$
for all integers
$\underline {\pi }_k(X)=0$
for all integers
![]() $k<n$
(resp.
$k<n$
(resp.
![]() $k> n$
). Observe that there are equivalences
$k> n$
). Observe that there are equivalences
Suppose
![]() $X,Y\in \mathrm {Sp}_G$
. By [Reference Hill, Hopkins and Ravenel29, Proposition 4.11],
$X,Y\in \mathrm {Sp}_G$
. By [Reference Hill, Hopkins and Ravenel29, Proposition 4.11],
![]() $X\in (\mathrm {Sp}_G)_{\geq 0}$
(resp.
$X\in (\mathrm {Sp}_G)_{\geq 0}$
(resp.
![]() $Y\in (\mathrm {Sp}_G)_{\leq -1}$
) if and only if X is slice
$Y\in (\mathrm {Sp}_G)_{\leq -1}$
) if and only if X is slice
![]() $(-1)$
-positive (resp. Y is slice
$(-1)$
-positive (resp. Y is slice
![]() $0$
-null) in the sense of [Reference Hill, Hopkins and Ravenel29, Definition 4.8]. This immediately implies the vanishing
$0$
-null) in the sense of [Reference Hill, Hopkins and Ravenel29, Definition 4.8]. This immediately implies the vanishing
for
![]() $X\in (\mathrm {Sp}_G)_{\geq 0}$
and
$X\in (\mathrm {Sp}_G)_{\geq 0}$
and
![]() $Y\in (\mathrm {Sp}_G)_{\leq -1}$
. According to [Reference Hill, Hopkins and Ravenel29, Remark 4.12], there is an example of
$Y\in (\mathrm {Sp}_G)_{\leq -1}$
. According to [Reference Hill, Hopkins and Ravenel29, Remark 4.12], there is an example of
![]() $X\in \mathrm {Sp}_G$
such that X is slice
$X\in \mathrm {Sp}_G$
such that X is slice
![]() $0$
-positive but
$0$
-positive but
![]() $X\notin (\mathrm {Sp}_G)_{\geq 1}$
.
$X\notin (\mathrm {Sp}_G)_{\geq 1}$
.
Suppose
![]() $X\in \mathrm {Sp}_G$
. As explained in [Reference Hill, Hopkins and Ravenel29, section 4.2], there exists a cofiber sequence in
$X\in \mathrm {Sp}_G$
. As explained in [Reference Hill, Hopkins and Ravenel29, section 4.2], there exists a cofiber sequence in
![]() $\mathrm {Sp}_G$
$\mathrm {Sp}_G$
such that
![]() $X'$
is slice
$X'$
is slice
![]() $(-1)$
-positive and
$(-1)$
-positive and
![]() $X"$
is slice
$X"$
is slice
![]() $0$
-null, that is,
$0$
-null, that is,
![]() $X'\in (\mathrm {Sp}_G)_{\geq 0}$
and
$X'\in (\mathrm {Sp}_G)_{\geq 0}$
and
![]() $X"\in (\mathrm {Sp}_G)_{\leq -1}$
.
$X"\in (\mathrm {Sp}_G)_{\leq -1}$
.
We combine what we have discussed above and recall the notion of t-structures in
![]() $\infty $
-categories from [Reference Lurie42, Definitions 1.2.1.1, 1.2.1.4] to deduce the following result, which is probably known to the experts.
$\infty $
-categories from [Reference Lurie42, Definitions 1.2.1.1, 1.2.1.4] to deduce the following result, which is probably known to the experts.
Proposition Appendix A.3.4. The pair of
![]() $(\mathrm {Sp}_G)_{\geq 0}$
and
$(\mathrm {Sp}_G)_{\geq 0}$
and
![]() $(\mathrm {Sp}_G)_{\leq 0}$
forms a t-structure on
$(\mathrm {Sp}_G)_{\leq 0}$
forms a t-structure on
![]() $\mathrm {Sp}_G$
.
$\mathrm {Sp}_G$
.
This t-structure is called the equivariant homotopy t-structure on
![]() $\mathrm {Sp}_G$
. By [Reference Lurie42, Remark 1.2.1.12], the heart
$\mathrm {Sp}_G$
. By [Reference Lurie42, Remark 1.2.1.12], the heart
![]() $\mathrm {Sp}_G^{\heartsuit }:=(\mathrm {Sp}_G)_{\geq 0}\cap (\mathrm {Sp}_G)_{\leq 0}$
is the nerve of an abelian category, and there is an equivalence
$\mathrm {Sp}_G^{\heartsuit }:=(\mathrm {Sp}_G)_{\geq 0}\cap (\mathrm {Sp}_G)_{\leq 0}$
is the nerve of an abelian category, and there is an equivalence
For every integer n, let
![]() $\tau _{\geq n}$
,
$\tau _{\geq n}$
,
![]() $\tau _{\leq n}$
and
$\tau _{\leq n}$
and
![]() $h_n$
denote the truncation and homology functors.
$h_n$
denote the truncation and homology functors.
Proposition Appendix A.3.5. The functor of
![]() $\infty $
-categories
$\infty $
-categories
sending
![]() $X\in \mathrm {Sp}_G^{\heartsuit }$
to
$X\in \mathrm {Sp}_G^{\heartsuit }$
to
![]() $\underline {\pi }_0(X)$
is an equivalence.
$\underline {\pi }_0(X)$
is an equivalence.
Proof. The functor (A.20) gives an equivalence
![]() $\mathrm {Mack}_G\simeq \mathrm {Ho}(\mathrm {Sp}_G^{\heartsuit })$
. Combine with equation (A.23) to obtain a quasi-inverse of equation (A.24).
$\mathrm {Mack}_G\simeq \mathrm {Ho}(\mathrm {Sp}_G^{\heartsuit })$
. Combine with equation (A.23) to obtain a quasi-inverse of equation (A.24).
Compose a quasi-inverse of equation (A.24) with the inclusion
![]() $\mathrm {Sp}_G^{\heartsuit } \to \mathrm {Sp}_G$
to obtain the functor of
$\mathrm {Sp}_G^{\heartsuit } \to \mathrm {Sp}_G$
to obtain the functor of
![]() $\infty $
-categories
$\infty $
-categories
which is an upgrade of equation (A.20).
Proposition Appendix A.3.6. The functor of
![]() $\infty $
-categories
$\infty $
-categories
![]() $\mathrm {H} \colon \mathrm {N}(\mathrm {Mack}_G) \to \mathrm {Sp}_G$
preserves products and filtered colimits.
$\mathrm {H} \colon \mathrm {N}(\mathrm {Mack}_G) \to \mathrm {Sp}_G$
preserves products and filtered colimits.
Proof. Owing to Proposition Appendix A.3.5, it remains to check that the inclusion functor
![]() $\mathrm {Sp}_G^{\heartsuit }\to \mathrm {Sp}_G$
preserves products and filtered colimits. This follows from Proposition Appendix A.3.2.
$\mathrm {Sp}_G^{\heartsuit }\to \mathrm {Sp}_G$
preserves products and filtered colimits. This follows from Proposition Appendix A.3.2.
Proposition Appendix A.3.7. Let H be a subgroup of G. Then the norm functor
![]() $i_{H \otimes }\colon \mathrm {Sp}_H \to \mathrm {Sp}_G$
sends
$i_{H \otimes }\colon \mathrm {Sp}_H \to \mathrm {Sp}_G$
sends
![]() $(\mathrm {Sp}_H)_{\geq 0}$
into
$(\mathrm {Sp}_H)_{\geq 0}$
into
![]() $(\mathrm {Sp}_G)_{\geq 0}$
.
$(\mathrm {Sp}_G)_{\geq 0}$
.
Proof. We refer to [Reference Hill, Hopkins and Ravenel29, Proposition 4.33].
A.4 Green functors
Our references for Green functors are [Reference Lewis37] and [Reference Shulman55].
Definition Appendix A.4.1. For Mackey functors M and L, the box product of M and L is defined to be
There is a purely algebraic definition of the box product of Mackey functors, which is rather explicit for
![]() $G=\mathbb {Z}/p$
and some prime p; see [Reference Lewis37, p. 61] and [Reference Shulman55, sections 2.2 and 2.4.3]. This is expected to coincide with the above Definition, but we won’t need this.
$G=\mathbb {Z}/p$
and some prime p; see [Reference Lewis37, p. 61] and [Reference Shulman55, sections 2.2 and 2.4.3]. This is expected to coincide with the above Definition, but we won’t need this.
Definition Appendix A.4.2. A Green functor A is a commutative monoid in the category
![]() $\mathrm {Mack}_G$
, that is, A is equipped with morphisms
$\mathrm {Mack}_G$
, that is, A is equipped with morphisms
![]() $A\Box A\to A$
and
$A\Box A\to A$
and
![]() $\underline {\pi }_0(\mathbb {S})\to A$
satisfying the unital, associative and commutative axioms, where
$\underline {\pi }_0(\mathbb {S})\to A$
satisfying the unital, associative and commutative axioms, where
![]() $\mathbb {S}$
denotes equivariant sphere spectrum. Let
$\mathbb {S}$
denotes equivariant sphere spectrum. Let
![]() $\mathrm {Green}_G$
denote the category of Green functors.
$\mathrm {Green}_G$
denote the category of Green functors.
An A-module M is an object of
![]() $\mathrm {Mack}_G$
equipped with an action morphism
$\mathrm {Mack}_G$
equipped with an action morphism
![]() $A\Box M\to M$
satisfying the module axioms.
$A\Box M\to M$
satisfying the module axioms.
For A-modules M and L,
![]() $M\Box _A L$
is defined to be the coequalizer of the two action morphisms
$M\Box _A L$
is defined to be the coequalizer of the two action morphisms
Let
![]() $\underline {\operatorname {\mathrm {Tor}}}_*^A(M,L)$
be the derived functor of
$\underline {\operatorname {\mathrm {Tor}}}_*^A(M,L)$
be the derived functor of
![]() $M\Box _A L$
.
$M\Box _A L$
.
Proposition Appendix A.4.3. Suppose
![]() $A\in \mathrm {CAlg}_G$
, and let M and L be A-modules. Then there exists a convergent spectral sequence
$A\in \mathrm {CAlg}_G$
, and let M and L be A-modules. Then there exists a convergent spectral sequence
Proof. We refer to [Reference Barwick, Glasman and Shah6, section 6]. With the stronger assumption
![]() $A\in \mathrm {NAlg}_G$
, this result is due to Lewis and Mandell [Reference Lewis and Mandell38, Theorem 6.6].
$A\in \mathrm {NAlg}_G$
, this result is due to Lewis and Mandell [Reference Lewis and Mandell38, Theorem 6.6].
Proposition Appendix A.4.4. Suppose
![]() $A\in \mathrm {CAlg}_G$
, and let M and L be A-modules. If A, M and L are
$A\in \mathrm {CAlg}_G$
, and let M and L be A-modules. If A, M and L are
![]() $(-1)$
-connected, then
$(-1)$
-connected, then
![]() $M\wedge _A L$
is
$M\wedge _A L$
is
![]() $(-1)$
-connected too, and there is an isomorphism
$(-1)$
-connected too, and there is an isomorphism
Proof. We refer to [Reference Barwick, Glasman and Shah6, Corollary 6.8.1].
Apply Proposition Appendix A.4.4 to the case when A is the equivariant sphere spectrum to obtain the symmetric monoidal structure on
![]() $(\mathrm {Sp}_G)_{\geq 0}$
that is the restriction of the symmetric monoidal structure on
$(\mathrm {Sp}_G)_{\geq 0}$
that is the restriction of the symmetric monoidal structure on
![]() $\mathrm {Sp}_G$
. Furthermore, the functor
$\mathrm {Sp}_G$
. Furthermore, the functor
is symmetric monoidal. Its right adjoint is the functor
![]() $\mathrm {H} \colon \mathrm {Mack}_G\to (\mathrm {Sp}_G)_{\geq 0}$
by Proposition Appendix A.3.5. Together with [Reference Lurie42, Remark 7.3.2.13], the induced functors
$\mathrm {H} \colon \mathrm {Mack}_G\to (\mathrm {Sp}_G)_{\geq 0}$
by Proposition Appendix A.3.5. Together with [Reference Lurie42, Remark 7.3.2.13], the induced functors
form an adjoint pair, where
![]() $(\mathrm {CAlg}_G)_{\geq 0}:=\mathrm {CAlg}((\mathrm {Sp}_G)_{\geq 0})$
. The formulation of these functors provided in [Reference Lurie42, Proposition 7.3.2.5] shows that the two squares in the diagram
$(\mathrm {CAlg}_G)_{\geq 0}:=\mathrm {CAlg}((\mathrm {Sp}_G)_{\geq 0})$
. The formulation of these functors provided in [Reference Lurie42, Proposition 7.3.2.5] shows that the two squares in the diagram

commute, where the vertical functors are the forgetful functors.
Suppose
![]() $A\in (\mathrm {CAlg}_G)_{\geq 0}$
. Let
$A\in (\mathrm {CAlg}_G)_{\geq 0}$
. Let
![]() $(\mathrm {Mod}_A)_{\geq 0}$
denote the
$(\mathrm {Mod}_A)_{\geq 0}$
denote the
![]() $\infty $
-category of A-modules in
$\infty $
-category of A-modules in
![]() $(\mathrm {Sp}_G)_{\geq 0}$
. By [Reference Patchkoria, Sanders and Wimmer47, Remark 3.8], we also have adjoint functors
$(\mathrm {Sp}_G)_{\geq 0}$
. By [Reference Patchkoria, Sanders and Wimmer47, Remark 3.8], we also have adjoint functors
such that the two squares in the diagram

commute, where the vertical functors are the forgetful functors.
Remark Appendix A.4.5. The equivariant Eilenberg–MacLane spectrum of a Green functor does not produce an object of
![]() $\mathrm {NAlg}_G$
in general; see [Reference Ullman57, Theorem 5.3, Proposition 6.1]. We need the stronger notion of Tambara functors to construct an object of
$\mathrm {NAlg}_G$
in general; see [Reference Ullman57, Theorem 5.3, Proposition 6.1]. We need the stronger notion of Tambara functors to construct an object of
![]() $\mathrm {NAlg}_G$
as the equivariant Eilenberg–MacLane spectrum. We refer to [Reference Ullman57] for the details.
$\mathrm {NAlg}_G$
as the equivariant Eilenberg–MacLane spectrum. We refer to [Reference Ullman57] for the details.
A.5 Flat modules
Definition Appendix A.5.1. Let A be a Green functor. An A-module M is called flat if the functor
![]() $M\Box _A (-)$
from the category of A-modules to the category of Mackey functors is exact. Equivalently,
$M\Box _A (-)$
from the category of A-modules to the category of Mackey functors is exact. Equivalently,
![]() $\underline {\operatorname {\mathrm {Tor}}}_s^{A}(-,M)=0$
for every integer
$\underline {\operatorname {\mathrm {Tor}}}_s^{A}(-,M)=0$
for every integer
![]() $s\geq 1$
. This definition was considered in [Reference Lewis and Mandell38, section 4].
$s\geq 1$
. This definition was considered in [Reference Lewis and Mandell38, section 4].
If
![]() $A\to B$
is a morphism of Green functors and M is a flat A-module, then
$A\to B$
is a morphism of Green functors and M is a flat A-module, then
![]() $M\Box _A B$
is a flat B-module.
$M\Box _A B$
is a flat B-module.
Definition Appendix A.5.2. Recall from [Reference Lewis and Mandell38, section 2] that the Burnside category
![]() $\mathfrak {B}_G$
is defined to be the additive category whose objects are the finite G-sets and whose hom groups are given by
$\mathfrak {B}_G$
is defined to be the additive category whose objects are the finite G-sets and whose hom groups are given by
for all finite G-sets X and Y.
For a finite G-set X, let
![]() $B^X$
denote the Mackey functor
$B^X$
denote the Mackey functor
![]() $\operatorname {\mathrm {Hom}}_{\mathfrak {B}_G}(-,X)$
. As explained in [Reference Lewis and Mandell38, p. 519], there is an isomorphism
$\operatorname {\mathrm {Hom}}_{\mathfrak {B}_G}(-,X)$
. As explained in [Reference Lewis and Mandell38, p. 519], there is an isomorphism
for all finite G-sets X and Y.
Proposition Appendix A.5.3. Let A be a Green functor. Then an A-module M is projective if and only if M is a direct summand of a direct sum of A-modules of the form
![]() $A\Box B^{G/H}$
, where H is a subgroup of G. Furthermore, every projective A-module is flat.
$A\Box B^{G/H}$
, where H is a subgroup of G. Furthermore, every projective A-module is flat.
Proof. These are nongraded versions of [Reference Lewis and Mandell38, Proposition 4.4, Theorem 4.5(c)]. See also [Reference Greenlees22, Corollary 1.5] for the first claim.
Definition Appendix A.5.4. Suppose
![]() $A\in \mathrm {CAlg}_G$
. An A-module M is called flat if the following two conditions are satisfied:
$A\in \mathrm {CAlg}_G$
. An A-module M is called flat if the following two conditions are satisfied:
-
(i)
 $\underline {\pi }_0(M)$
is a flat
$\underline {\pi }_0(M)$
is a flat
 $\underline {\pi }_0(A)$
-module,
$\underline {\pi }_0(A)$
-module, -
(ii) the induced map
is an isomorphism for every integer n. $$\begin{align*}\underline{\pi}_n(A)\Box_{\underline{\pi}_0(A)}\underline{\pi}_0(M) \to \underline{\pi}_n(M) \end{align*}$$
$$\begin{align*}\underline{\pi}_n(A)\Box_{\underline{\pi}_0(A)}\underline{\pi}_0(M) \to \underline{\pi}_n(M) \end{align*}$$
Proposition Appendix A.5.5. Let
![]() $A\to B$
be a map in
$A\to B$
be a map in
![]() $\mathrm {CAlg}_G$
, and let M be a flat A-module. Then
$\mathrm {CAlg}_G$
, and let M be a flat A-module. Then
![]() $B\wedge _A M$
is a flat B-module. Consequently, if we have maps
$B\wedge _A M$
is a flat B-module. Consequently, if we have maps
![]() $A \to B$
,
$A \to B$
,
![]() $A \to C$
and
$A \to C$
and
![]() $B \to L$
in
$B \to L$
in
![]() $\mathrm {CAlg}_G$
such that L is a flat B-module, then the induced map
$\mathrm {CAlg}_G$
such that L is a flat B-module, then the induced map
![]() $B \wedge _A C \to L \wedge _A C$
is flat.
$B \wedge _A C \to L \wedge _A C$
is flat.
Proof. The conditions (i) and (ii) in Definition Appendix A.5.4 for M imply that
![]() $\underline {\pi }_*(M)$
is a flat
$\underline {\pi }_*(M)$
is a flat
![]() $\underline {\pi }_*(A)$
-module. This means
$\underline {\pi }_*(A)$
-module. This means
![]() $\underline {\operatorname {\mathrm {Tor}}}_{p}^{\underline {\pi }_*(A)}(-,\underline {\pi }_*(M))_q=0$
for all integers
$\underline {\operatorname {\mathrm {Tor}}}_{p}^{\underline {\pi }_*(A)}(-,\underline {\pi }_*(M))_q=0$
for all integers
![]() $p\geq 1$
and q. Together with the convergent spectral sequence
$p\geq 1$
and q. Together with the convergent spectral sequence
obtained from Proposition Appendix A.4.3, we obtain isomorphisms of Mackey functors
 $$ \begin{align*} \underline{\pi}_n(B)\Box_{\underline{\pi}_0(A)}\underline{\pi}_0(M) \cong & (\underline{\pi}_*(B)\Box_{\underline{\pi}_0(A)}\underline{\pi}_0(M))_n \\ \cong &(\underline{\pi}_*(B)\Box_{\underline{\pi}_*(A)}\underline{\pi}_*(M))_n \cong\underline{\pi}_n(B\wedge_A M)\\[-17pt] \end{align*} $$
$$ \begin{align*} \underline{\pi}_n(B)\Box_{\underline{\pi}_0(A)}\underline{\pi}_0(M) \cong & (\underline{\pi}_*(B)\Box_{\underline{\pi}_0(A)}\underline{\pi}_0(M))_n \\ \cong &(\underline{\pi}_*(B)\Box_{\underline{\pi}_*(A)}\underline{\pi}_*(M))_n \cong\underline{\pi}_n(B\wedge_A M)\\[-17pt] \end{align*} $$
for all integers n. This implies the conditions (i) and (ii) in Definition Appendix A.5.4 for
![]() $B\wedge _A M$
. The second statement follows from the first applied to
$B\wedge _A M$
. The second statement follows from the first applied to
![]() $B \to B \wedge _A C$
.
$B \to B \wedge _A C$
.
Proposition Appendix A.5.6. Let
![]() $f\colon A\to B$
be a flat map in
$f\colon A\to B$
be a flat map in
![]() $\mathrm {CAlg}_G$
. If the induced morphism
$\mathrm {CAlg}_G$
. If the induced morphism
![]() $\underline {\pi }_0(A)\to \underline {\pi }_0(B)$
is an isomorphism, then f is an equivalence.
$\underline {\pi }_0(A)\to \underline {\pi }_0(B)$
is an isomorphism, then f is an equivalence.
Proof. Immediate from the condition (ii) in Definition Appendix A.5.4.
Proposition Appendix A.5.7. Let A be a Green functor, and let M and L be A-modules. If M is flat, then there is an equivalence
Proof. From the convergent spectral sequence
obtained from Proposition Appendix A.4.3, we have
for every nonzero integer k.
Proposition Appendix A.5.8. Let A be a Green functor. If
![]() $\mathop {\mathrm {colim}}_{i\in I}M_i$
is a filtered colimit of A-modules and L is an A-module, then there is a canonical equivalence
$\mathop {\mathrm {colim}}_{i\in I}M_i$
is a filtered colimit of A-modules and L is an A-module, then there is a canonical equivalence
Proof. Since
![]() $\wedge $
commutes with colimits in each variable, we have a canonical equivalence
$\wedge $
commutes with colimits in each variable, we have a canonical equivalence
Apply
![]() $\underline {\pi }_0$
to this, and use Propositions Appendix A.3.2, Appendix A.3.6 and Appendix A.4.4 to obtain the desired equivalence.
$\underline {\pi }_0$
to this, and use Propositions Appendix A.3.2, Appendix A.3.6 and Appendix A.4.4 to obtain the desired equivalence.
Proposition Appendix A.5.9. Let A be a Green functor, and let
be a system of exact sequence of A-modules over a filtered category I. Then the induced sequence
is exact.
Proof. We have a system of cofiber sequences in
![]() $\mathrm {Sp}_G$
$\mathrm {Sp}_G$
Take colimits and use Proposition Appendix A.3.6 to obtain a cofiber sequence
Together with the fact that cofiber sequences and exact sequences coincide in the heart of a t-structure, we deduce the claim.
Proposition Appendix A.5.10. Let A be a Green functor. Then every filtered colimit
![]() $\mathop {\mathrm {colim}}_{i\in I} M_i$
of flat A-modules is flat.
$\mathop {\mathrm {colim}}_{i\in I} M_i$
of flat A-modules is flat.
Proof. Let
![]() $0\to L'\to L\to L"\to 0$
be an exact sequence of A-modules. Then the induced sequence
$0\to L'\to L\to L"\to 0$
be an exact sequence of A-modules. Then the induced sequence
![]() $0\to M_i\Box _A L'\to M_i\Box _A L\to M_i\Box _A L"\to 0$
is exact, so the induced sequence
$0\to M_i\Box _A L'\to M_i\Box _A L\to M_i\Box _A L"\to 0$
is exact, so the induced sequence
is exact too by Proposition Appendix A.5.9. Combine with Proposition Appendix A.5.8 to conclude.
Proposition Appendix A.5.11. Suppose
![]() $A\in \mathrm {CAlg}_G$
. Then every filtered colimit of flat A-modules is flat. In particular, every filtered colimit of free A-modules is flat.
$A\in \mathrm {CAlg}_G$
. Then every filtered colimit of flat A-modules is flat. In particular, every filtered colimit of free A-modules is flat.
Acknowledgements
This research was conducted in the framework of the DFG-funded research training group GRK 2240: Algebro- Geometric Methods in Algebra, Arithmetic and Topology. We are pleased to thank the referee for a very precise and helpful report.
Competing Interests
The authors declare none.