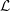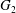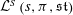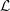Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ginzburg, David
and
Hundley, Joseph
2015.
A doubling integral for G 2.
Israel Journal of Mathematics,
Vol. 207,
Issue. 2,
p.
835.
Segal, Avner
2016.
A Family of New-Way Integrals for the Standard ℒ-function of Cuspidal Representations of the Exceptional Group of TypeG2.
International Mathematics Research Notices,
p.
rnw090.
Gao, Fan
Shahidi, Freydoon
and
Szpruch, Dani
2018.
Geometry, Algebra, Number Theory, and Their Information Technology Applications.
Vol. 251,
Issue. ,
p.
207.
Segal, Avner
2018.
The degenerate Eisenstein series attached to the Heisenberg parabolic subgroups of quasi-split forms of 𝑆𝑝𝑖𝑛₈.
Transactions of the American Mathematical Society,
Vol. 370,
Issue. 8,
p.
5983.
Gurevich, Nadya
and
Segal, Avner
2019.
Poles of the Standard -function of and the Rallis–Schiffmann Lift.
Canadian Journal of Mathematics,
Vol. 71,
Issue. 5,
p.
1127.
Pollack, Aaron
2021.
Relative Trace Formulas.
p.
379.
Friedberg, Solomon
and
Ginzburg, David
2021.
Relative Trace Formulas.
p.
75.
Çiçek, Fatma
Davidoff, Giuliana
Dijols, Sarah
Hammonds, Trajan
Pollack, Aaron
and
Roy, Manami
2022.
The completed standard L-function of modular forms on $$G_2$$.
Mathematische Zeitschrift,
Vol. 302,
Issue. 1,
p.
483.
Jin, Yubo
and
Yan, Pan
2025.
L-functions for Sp(2n) × GL(k) via Non-unique Models.
International Mathematics Research Notices,
Vol. 2025,
Issue. 5,