Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T14:08:13.641Z Has data issue: false hasContentIssue false
  • English
  • Français

THE RANGE OF TREE-INDEXED RANDOM WALK

Part of: Markov processes Stochastic processes

Published online by Cambridge University Press:  10 September 2014

Jean-François Le Gall  and
Shen Lin
Jean-François Le Gall
Affiliation:
Université Paris-Sud, France
Shen Lin
Affiliation:
Université Paris-Sud, France
Get access Rights & Permissions [Opens in a new window]

Abstract

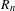We provide asymptotics for the range $R_{n}$ of a random walk on the 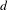$d$-dimensional lattice indexed by a random tree with $n$ vertices. Using Kingman’s subadditive ergodic theorem, we prove under general assumptions that 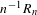$n^{-1}R_{n}$ converges to a constant, and we give conditions ensuring that the limiting constant is strictly positive. On the other hand, in dimension $4$, and in the case of a symmetric random walk with exponential moments, we prove that 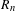$R_{n}$ grows like 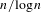$n/\!\log n$. We apply our results to asymptotics for the range of a branching random walk when the initial size of the population tends to infinity.

Keywords

tree-indexed random walkrangediscrete snakebranching random walksubadditive ergodic theorem

MSC classification

Primary: 60G50: Sums of independent random variables; random walks 60J80: Branching processes (Galton-Watson, birth-and-death, etc.)
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 15 , Issue 2 , April 2016 , pp. 271 - 317
Copyright
© Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abraham, R. and Werner, W., Avoiding probabilities for Brownian snakes and super-Brownian motion, Electron. J. Probab. 2(3) (1997), 27.CrossRefGoogle Scholar
Delmas, J.-F., Some properties of the range of super-Brownian motion, Probab. Theory Related Fields 114 (1999), 505–547.CrossRefGoogle Scholar
Duquesne, T. and Le Gall, J.-F., Random Trees, Lévy Processes and Spatial Branching Processes, Astérisque 281 (2002).Google Scholar
Dvoretzky, A. and Erdös, P., Some problems on random walk in space, in Proceedings Second Berkeley Symposium on Math. Statistics and Probability, pp. 353–367 (University of California Press, Berkeley, 1951).Google Scholar
Jain, N. C. and Pruitt, W. E., The range of transient random walk, J. Anal. Math. 24 (1971), 369–393.CrossRefGoogle Scholar
Jain, N. C. and Pruitt, W. E., The range of random walk, in Proceedings Sixth Berkeley Symposium on Mathematical Statistics and Probability, Volume III: Probability theory, pp. 31–50 (University of California Press, Berkeley, 1972).Google Scholar
Janson, S., Random cutting and records in deterministic and random trees, Random Structures Algorithms 29 (2006), 139–179.CrossRefGoogle Scholar
Janson, S. and Marckert, J.-F., Convergence of discrete snakes, J. Theoret. Probab. 18 (2005), 615–647.CrossRefGoogle Scholar
Kesten, H., Branching random walk with a critical branching part, J. Theoret. Probab. 8 (1995), 921–962.CrossRefGoogle Scholar
Kingman, J. F. C., The ergodic theory of subadditive stochastic processes, J. R. Stat. Soc. Ser.B 30 (1968), 499–510.Google Scholar
Kortchemski, I., A simple proof of Duquesne’s theorem on contour processes of conditioned Galton-Watson trees, in Séminaire de Probabilités XLV, Lecture Notes in Mathematics, Volume 2078, pp. 537–558 (Springer, Berlin, 2013).CrossRefGoogle Scholar
Lalley, S. and Zheng, X., Occupation statistics of critical branching random walks in two or higher dimensions, Ann. Probab. 39 (2011), 327–368.CrossRefGoogle Scholar
Lawler, G. F., personal communication.Google Scholar
Lawler, G. F. and Limic, V., Random Walk: A Modern Introduction, Cambridge Studies in Advanced Mathematics, Volume 123 (Cambridge University Press, Cambridge, 2010).CrossRefGoogle Scholar
Le Gall, J.-F., Propriétés d’intersection des marches aléatoires I, Comm. Math. Physics 104 (1986), 471–507.CrossRefGoogle Scholar
Le Gall, J.-F., Random trees and applications, Probab. Surv. 2 (2005), 245–311.CrossRefGoogle Scholar
Le Gall, J.-F., Itô’s excursion theory and random trees, Stochastics Process. Appl. 120 (2010), 721–749.CrossRefGoogle Scholar
Le Gall, J.-F. and Lin, S., The range of tree-indexed random walk in low dimensions, Ann. Probab., to appear.Google Scholar
Le Gall, J.-F. and Rosen, J., The range of stable random walks, Ann. Probab. 16 (1991), 650–705.Google Scholar
Lin, S., The range of tree-indexed random walk with drift, in preparation.Google Scholar
Lyons, R., Pemantle, R. and Peres, Y., Conceptual proofs of LlogL criteria for mean behavior of branching processes, Ann. Probab. 23 (1995), 1125–1138.CrossRefGoogle Scholar
Marcus, M. B. and Rosen, J., Laws of the iterated logarithm for intersections of random walks on ℤ4, Ann. Inst. Henri Poincaré Probab. Stat. 33 (1997), 37–63.CrossRefGoogle Scholar
Pitman, J. W., One-dimensional Brownian motion and the three-dimensional Bessel process, Adv. Appl. Probab. 7 (1975), 511–526.CrossRefGoogle Scholar
Pitman, J. W., Combinatorial Stochastic Processes, Lectures from the 32nd Summer School on Probability Theory held in Saint-Flour, July 7–24, 2002, Lecture Notes in Mathematics, Volume 1875 (Springer, Berlin, 2006).Google Scholar
Revuz, D. and Yor, M., Continuous Martingales and Brownian Motion (Springer, Berlin, 1991).CrossRefGoogle Scholar
Zaitsev, A. Y., Multidimensional version of the results of Komlós, Major and Tusnády for vectors with finite exponential moments, ESAIM Probab. Stat. 2 (1998), 41–108.CrossRefGoogle Scholar