Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-10T23:21:34.779Z Has data issue: false hasContentIssue false
  • English
  • Français

PROPAGATION OF SINGULARITIES ON AdS SPACETIMES FOR GENERAL BOUNDARY CONDITIONS AND THE HOLOGRAPHIC HADAMARD CONDITION

Published online by Cambridge University Press:  18 March 2020

Oran Gannot  and
Michał Wrochna Open the ORCID record for Michał Wrochna [Opens in a new window]
Oran Gannot
Affiliation:
Department of Mathematics, Lunt Hall, Northwestern University, Evanston, IL60208, USA ([email protected])
Michał Wrochna
Affiliation:
Université de Cergy-Pontoise, 2 av. Adolphe Chauvin, 95302 Cergy-Pontoise Cedex, France ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the Klein–Gordon equation on asymptotically anti-de-Sitter spacetimes subject to Neumann or Robin (or Dirichlet) boundary conditions and prove propagation of singularities along generalized broken bicharacteristics. The result is formulated in terms of conormal regularity relative to a twisted Sobolev space. 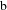We use this to show the uniqueness, modulo regularizing terms, of parametrices with prescribed $\text{b}$-wavefront set. Furthermore, in the context of quantum fields, we show a similar result for two-point functions satisfying a holographic Hadamard condition on the 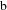$\text{b}$-wavefront set.

Keywords

propagation of singularitiesKlein–Gordon equationanti-de Sitter spacetimesquantum field theory on curved spacetimesHadamard states
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 1 , January 2022 , pp. 67 - 127
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Albin, P., A renormalized index theorem for some complete asymptotically regular metrics: the Gauss–Bonnet theorem, Adv. Math. 213(1) (2007), 1–52.CrossRefGoogle Scholar
Bachelot, A., The Klein–Gordon equation in the anti-de Sitter cosmology, J. Math. Pures Appl. 96(6) (2011), 527–554.CrossRefGoogle Scholar
Breitenlohner, P. and Freedman, D. Z., Positive energy in anti-de Sitter backgrounds and gauged extended supergravity, Phys. Lett. B 115(3) (1982), 197–201.CrossRefGoogle Scholar
Breitenlohner, P. and Freedman, D. Z., Stability in gauged extended supergravity, Ann. Phys. 144(2) (1982), 249–281.CrossRefGoogle Scholar
Belokogne, A., Folacci, A. and Queva, J., Stueckelberg massive electromagnetism in de Sitter and anti–de Sitter spacetimes: Two-point functions and renormalized stress-energy tensors, Phys. Rev. D 94(10) (2016), 105028.CrossRefGoogle Scholar
Chang, S.-Y. A. and Gonzalez, M. del M., Fractional Laplacian in conformal geometry, Adv. Math. 226(2) (2011), 1410–1432.CrossRefGoogle Scholar
Dappiaggi, C., Drago, N. and Ferreira, H., Fundamental solutions for the wave operator on static Lorentzian manifolds with timelike boundary, Lett. Math. Phys. 109(10) (2018), 2157–2186.CrossRefGoogle Scholar
Dappiaggi, C. and Ferreira, H., Hadamard states for a scalar field in anti–de Sitter spacetime with arbitrary boundary conditions, Phys. Rev. D 94(12) (2016), 125016.CrossRefGoogle Scholar
Dappiaggi, C. and Ferreira, H., On the algebraic quantization of a massive scalar field in anti-de Sitter spacetime, Rev. Math. Phys. 30(02) (2018), 1850004.CrossRefGoogle Scholar
Dappiaggi, C., Ferreira, H. and Marta, A., Ground states of a Klein-Gordon field with Robin boundary conditions in global anti-de Sitter spacetime, Phys. Rev. D 98 (2018), 025005.CrossRefGoogle Scholar
Duistermaat, J. J. and Hörmander, L., Fourier integral operators. II, Acta Math. 128(1) (1972), 183–269.CrossRefGoogle Scholar
Dybalski, W. and Wrochna, M., A mechanism for holography for non-interacting fields on anti-de Sitter spacetimes, Class. Quant. Grav. 36(8) (2019), 085006.CrossRefGoogle Scholar
Enciso, A., del Mar González, M. and Vergara, B., Fractional powers of the wave operator via Dirichlet-to-Neumann maps in anti-de Sitter spaces, J. Funct. Anal. 273(6) (2017), 2144–2166.CrossRefGoogle Scholar
Enciso, A. and Kamran, N., A singular initial-boundary value problem for nonlinear wave equations and holography in asymptotically anti-de Sitter spaces, J. Math. Pures Appl. 103(4) (2015), 1053–1091.CrossRefGoogle Scholar
Galstian, A., L p -L q -Decay estimates for the Klein-Gordon equation in the anti-de Sitter space-time, Rend. Istit. Mat. Univ. Trieste 42 (2010), 27–50.Google Scholar
Gannot, O., Elliptic boundary value problems for Bessel operators, with applications to anti-de Sitter spacetimes, C. R. Math. 356(10) (2018), 988–1029.CrossRefGoogle Scholar
Graham, C. R. and Lee, J. M., Einstein metrics with prescribed conformal infinity on the ball, Adv. Math. 87(2) (1991), 186–225.CrossRefGoogle Scholar
Nogueras, M. del M. G. and Qing, J., Fractional conformal Laplacians and fractional Yamabe problems, Anal. PDE 6(7) (2013), 1535–1576.CrossRefGoogle Scholar
Gérard, C., Oulghazi, O. and Wrochna, M., Hadamard states for the Klein–Gordon equation on Lorentzian manifolds of bounded geometry, Comm. Math. Phys. 352(2) (2017), 519–583.CrossRefGoogle Scholar
Grisvard, P., Espaces intermédiaires entre espaces de Sobolev avec poids, Ann. Sc. Norm. Super. Pisa Cl. Sci. 17(3) (1963), 255–296.Google Scholar
Guillarmou, C., Meromorphic properties of the resolvent on asymptotically hyperbolic manifolds, Duke Math. J. 129(1) (2005), 1–37.CrossRefGoogle Scholar
Hintz, P., 18.157: Introduction to Microlocal Analysis, Lecture Notes (2019).Google Scholar
Holzegel, G., Well-posedness for the massive wave equation on asymptotically anti-de Sitter spacetimes, J. Hyperbolic Differ. Equ. 9(02) (2012), 239–261.CrossRefGoogle Scholar
Hörmander, L., The Analysis of Linear Partial Differential Operators III: Pseudo-Differential Operators, Grundlehren der mathematischen Wissenschaften, (Springer, Berlin Heidelberg, 1994).Google Scholar
Holzegel, G. and Shao, A., Unique continuation from infinity in asymptotically anti-de Sitter spacetimes, Comm. Math. Phys. 347(3) (2016), 723–775.CrossRefGoogle Scholar
Holzegel, G. and Shao, A., Unique continuation from infinity in asymptotically anti-de Sitter spacetimes II: Non-static boundaries, Comm. Partial Differential Equations 42(12) (2017), 1871–1922.CrossRefGoogle Scholar
Holzegel, G. and Smulevici, J., Decay properties of Klein-Gordon fields on Kerr-Ads spacetimes, Comm. Pure Appl. Math. 66(11) (2013), 1751–1802.CrossRefGoogle Scholar
Holzegel, G. H. and Warnick, C. M., Boundedness and growth for the massive wave equation on asymptotically anti-de Sitter black holes, J. Funct. Anal. 266(4) (2014), 2436–2485.CrossRefGoogle Scholar
Kent, C. and Winstanley, E., Hadamard renormalized scalar field theory on anti–de Sitter spacetime, Phys. Rev. D 91 (2015), 044044.CrossRefGoogle Scholar
Lebeau, G., Propagation des ondes dans les variétés à coins, Ann. Sci. Éc. Norm. Supér. 30(4) (1997), 429–497.CrossRefGoogle Scholar
Mazzeo, R., Elliptic theory of differential edge operators I, Comm. Partial Differential Equations 16(10) (1991), 1615–1664.Google Scholar
Melrose, R., The Atiyah-Patodi-Singer Index Theorem, Research Notes in Mathematics, (Taylor & Francis, New York, 1993).CrossRefGoogle Scholar
Melrose, R. B., Transformation of boundary problems, Acta Math. 147(1) (1981), 149–236.CrossRefGoogle Scholar
Melrose, R. B. and Sjöstrand, J., Singularities of boundary value problems. i, Comm. Pure Appl. Math. 31(5) (1978), 593–617.CrossRefGoogle Scholar
Melrose, R. B. and Sjöstrand, J., Singularities of boundary value problems. ii, Comm. Pure Appl. Math. 35(2) (1982), 129–168.CrossRefGoogle Scholar
Mazzeo, R. and Vertman, B., Elliptic theory of differential edge operators, II: boundary value problems, Indiana Univ. Math. J. (2014), 1911–1955.CrossRefGoogle Scholar
Melrose, R., Vasy, A. and Wunsch, J., Propagation of singularities for the wave equation on edge manifolds, Duke Math. J. 144(1) (2008), 109–193.CrossRefGoogle Scholar
Pham, H., A simple diffractive boundary value problem on an asymptotically anti-de Sitter space, in Microlocal Methods in Mathematical Physics and Global Analysis, pp. 133–136 (Springer, Basel, 2013).CrossRefGoogle Scholar
Radzikowski, M. J., Micro-local approach to the Hadamard condition in quantum field theory on curved space-time, Comm. Math. Phys. 179(3) (1996), 529–553.CrossRefGoogle Scholar
Sanders, K., Equivalence of the (generalised) Hadamard and microlocal spectrum condition for (generalised) free fields in curved spacetime, Comm. Math. Phys. 295(2) (2010), 485–501.CrossRefGoogle Scholar
Sjöstrand, J., Analytic singularities of solutions of boundary value problems, in Singularities in Boundary Value Problems, pp. 235–269 (Springer, Dordrecht, 1981).CrossRefGoogle Scholar
Taylor, M. E., Grazing rays and reflection of singularities of solutions to wave equations, Comm. Pure Appl. Math. 29(1) (1976), 1–38.CrossRefGoogle Scholar
Vasy, A., Propagation of singularities for the wave equation on manifolds with corners, Sémin. Équ. Dériv. Partielles 2004 (2004), 1–16.Google Scholar
Vasy, A., Propagation of singularities for the wave equation on manifolds with corners, Ann. of Math. (2) (2008), 749–812.CrossRefGoogle Scholar
Vasy, A., Diffraction at corners for the wave equation on differential forms, Comm. Partial Differential Equations 35(7) (2010), 1236–1275.CrossRefGoogle Scholar
Vasy, A., The wave equation on asymptotically anti de Sitter spaces, Anal. PDE 5(1) (2012), 81–144.CrossRefGoogle Scholar
Warnick, C. M., The massive wave equation in asymptotically Ads spacetimes, Comm. Math. Phys. 321(1) (2013), 85–111.CrossRefGoogle Scholar
Warnick, C. M., On quasinormal modes of asymptotically anti-de Sitter black holes, Comm. Math. Phys. 2(333) (2015), 959–1035.CrossRefGoogle Scholar
Wrochna, M., The holographic Hadamard condition on asymptotically anti-de Sitter spacetimes, Lett. Math. Phys. 107(12) (2017), 2291–2331.CrossRefGoogle Scholar
Yagdjian, K. and Galstian, A., The Klein-Gordon equation in anti-de Sitter spacetime, Rend. Semin. Mat. Univ. Politec. Torino 67(2) (2009), 271–292.Google Scholar