Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-11T02:04:38.125Z Has data issue: false hasContentIssue false
  • English
  • Français

Product formula for p -adic epsilon factors

Part of: Algebraic number theory: local and $p$-adic fields (Co)homology theory

Published online by Cambridge University Press:  08 May 2014

Tomoyuki Abe  and
Adriano Marmora
Tomoyuki Abe
Affiliation:
Kavli Institute for the Physics and Mathematics of the Universe (WPI), The University of Tokyo, 5-1-5 Kashiwanoha, Kashiwa, Chiba, 277-8583, Japan ([email protected])
Adriano Marmora
Affiliation:
Institut de Recherche Mathématique Avancée, UMR 7501, Université de Strasbourg et CNRS, 7 rue René Descartes, 67000 Strasbourg, France ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 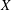$X$ be a smooth proper curve over a finite field of characteristic 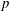$p$. We prove a product formula for 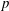$p$-adic epsilon factors of arithmetic 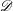$\mathscr{D}$-modules on 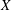$X$. In particular we deduce the analogous formula for overconvergent 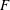$F$-isocrystals, which was conjectured previously. The 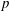$p$-adic product formula is a counterpart in rigid cohomology of the Deligne–Laumon formula for epsilon factors in 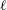$\ell$-adic étale cohomology (for 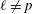$\ell \neq p$). One of the main tools in the proof of this 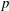$p$-adic formula is a theorem of regular stationary phase for arithmetic 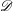$\mathscr{D}$-modules that we prove by microlocal techniques.

Keywords

rigid cohomologyp-adic differential equationsarithmetic D-modulesp-adic Fourier transformepsilon factors

MSC classification

Primary: 14F30: $p$-adic cohomology, crystalline cohomology
Secondary: 11S40: Zeta functions and $L$-functions
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 14 , Issue 2 , April 2015 , pp. 275 - 377
Copyright
© Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abbes, A. and Saito, T., Local Fourier transform and epsilon factors, Compos. Math. 146 (2010), 1507–1551.CrossRefGoogle Scholar
Abe, T., Comparison between Swan conductors and characteristic cycles, Compos. Math. 146 (2010), 638–682.CrossRefGoogle Scholar
Abe, T., 2011 Rings of microdifferential operators for arithmetic $\mathscr{D}$ -modules, Preprint arXiv:1104.1574v3 12 Mar, 2014.Google Scholar
Abe, T., Explicit calculation of Frobenius isomorphisms and Poincaré duality in the theory of arithmetic D-modules, Rend. Semin. Mat. Univ. Padova (in press).Google Scholar
Abe, T., 2011 Langlands program for $p$ -adic coefficients and the petites camarades conjecture, Preprint arXiv:1111.2479v1 10 Nov.Google Scholar
Abe, T., 2013 Langlands correspondence for isocrystals and existence of crystalline companion for curves, Preprint arXiv:1310.0528 2 Oct.Google Scholar
Abe, T. and Caro, D., 2013 Theory of weights in $p$ -adic cohomology, Preprint arXiv:1303.0662v2 14 May.Google Scholar
Arabia, A. D. and Mebkhout, Z., Sur le topos infinitésimal p-adique d’un schéma lisse I, Ann. Inst. Fourier (Grenoble) 60(6) (2010).Google Scholar
Baldassarri, F. and Berthelot, P., On Dwork cohomology for singular hypersurfaces, in Geometric Aspects of Dwork Theory, Volume I, pp. 177–244 (Walter de Gruyter, Berlin, 2004).CrossRefGoogle Scholar
Berthelot, P., Cohomologie rigide et théorie de Dwork, Astérisque 119–120 (1984), 17–49.Google Scholar
Berthelot, P., Cohomolgie rigide et théorie des D-modules, Lecture Notes in Math., Volume 1454, pp. 80–124 (Springer, Berlin, 1990).Google Scholar
Berthelot, P., 1996 Cohomologie rigide et cohomologie rigide à supports propres. Premiére partie (version provisoire 1991) Prépublication IRMR 96-03.Google Scholar
Berthelot, P., D-modules arithmétiques I. Opérateurs différentiels de niveau fini, Ann. Sci. École Norm. Sup. (4) 29(2) (1996), 185–272.Google Scholar
Berthelot, P., Dualité de Poincaré et formule de Künneth en cohomologie rigide, C. R. Acad. Sci. Paris 325 (1997), 493–498.Google Scholar
Berthelot, P., D-modules arithmétiques II. Descente par Frobenius, Mém. Soc. Math. Fr. 81 (2000).Google Scholar
Berthelot, P., Introduction à la théorie arithmétique des D-modules, Astérisque 279 (2002), 1–80.Google Scholar
Berthelot, P., Letter to D. Caro, on June 22, 2007.Google Scholar
Bourbaki, N., Algèbre Commutative. (Hermann, Paris).Google Scholar
Bosch, S., Güntzer, U. and Remmert, R., Non-Archimedean Analysis, Grundlehren der Math., Wissenschaften, Volume 261 (Springer, Berlin, 1984).Google Scholar
Björk, J. E., Analytic D-Modules and Applications, Mathematics and its Applications, Volume 247 (Kluwer, Dordrecht, 1993).Google Scholar
Caro, D., D-modules arithmétiques surcohérents. Application aux fonctions L , Ann. Inst. Fourier 54 (2005), 1943–1996.CrossRefGoogle Scholar
Caro, D., Fonctions L associées aux D-modulles arithmétiques. Cas des courbes, Compos. Math. 142 (2006), 169–206.Google Scholar
Chiarellotto, B. and Le Stum, B., F-isocristaux unipotents, Compos. Math. 116 (1999), 81–110.Google Scholar
Christol, G., Systèmes différentiels linéaires p-adiques, structure de Frobenius faible, Bull. Soc. Maths France 109(1) (1981), 83–122.CrossRefGoogle Scholar
Christol, G. and Mebkhout, Z., Équations différentielles p-adiques et coefficients p-adiques sur les courbes, Astérisque 279 (2002), 125–183.Google Scholar
Christol, G. and Mebkhout, Z., Sur le théorème de l’indice des équations différentielles p-adiques IV, Invent. Math. 143 (2001), 629–672.Google Scholar
Crew, R., F-isocrystals and their monodromy groups, Ann. Sci. École Norm. Sup. (4) 25(4) (1992), 429–464.Google Scholar
Crew, R., Finiteness theorems for the cohomology of an overconvergent isocrystal on a curve, Ann. Sci. École Norm. Sup. (4) 31(6) (1998), 717–763.Google Scholar
Crew, R., Canonical extensions, irregularities, and the Swan conductor, Math. Ann. 316 (2000), 19–37.Google Scholar
Crew, R., Arithmetic D-modules on a formal curve, Math. Ann. 336(2) (2006), 439–448.Google Scholar
Crew, R., Arithmetic D-modules on the unit disk. With an appendix by Shigeki Matsuda, Compos. Math. 148 (2012), 227–268.Google Scholar
Deligne, P., Les constantes des équations fonctionnelles des fonctions L, Lecture Notes in Math., Volume 349, pp. 501–597 (Springer, Berlin, 1973).Google Scholar
Deligne, P., Les constantes des équations fonctionelles des fonctions $L$ , Séminaire à l’I.H.E.S. (1980).Google Scholar
Deligne, P., La conjecture de Weil.II, Publ. Math. Inst. Hautes Éudes Sci. 52 (1981), 313–428.Google Scholar
Deligne, P. and Milne, J. S., Tannakian Categories, Lecture Notes in Math., Volume 900, pp. 101–228 (Springer, Berlin, 1982).Google Scholar
Dwork, B., On exponents of p-adic differential modules, J. Reine Angew. Math. 484 (1997), 85–126.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique I-IV, Publ. Math. Inst. Hautes Éudes Sci. 4 (1960), 8 11 (1961), 17 (1963), 20 (1964), 24 (1965), 28 (1966), 32 (1967).Google Scholar
Etesse, J. -Y. and Le Stum, B., Fonctions L associèes aux F-isocristaux surconvergent I. Interprétation cohomologique, Math. Ann. 296 (1993), 557–576.Google Scholar
Fontaine, J. M., Représentations ℓ-adiques potentiellement semi-stables, Astérisque 223 (1994), 321–347.Google Scholar
Garnier, L., Théorèmes de division sur D̂Xℚ (0) et applications, Bull. Soc. Maths France 123(4) (1995), 547–589.Google Scholar
Garnier, L., Cohérence sur D† et irrégularité des isocristaux surconvergents de rang 1, Forum Math. 9 (1997), 569–601.Google Scholar
Garnier, L., Descente par Frobenius explicite pour les D †-modules, J. Algebra 205 (1998), 542–577.Google Scholar
Katz, N., Travaux de Laumon, Sem. Bourb. Exp. 691 (1988).Google Scholar
Kedlaya, K. S., Full faithfulness for overconvergent F-isocrystals, in Geometric Aspects of Dwork Theory, Volume II, pp. 819–835 (de Gruyter, Berlin, 2004).CrossRefGoogle Scholar
Kedlaya, K. S., Slope filtration revisited, Documenta Math. 10 (2005), 447–525.Google Scholar
Kedlaya, K. S., Finiteness of rigid cohomology with coefficients, Duke Math. J. 134 (2006), 15–97.Google Scholar
Kedlaya, K. S., p-adic Differential Equations, Cambridge Studies in Advanced Mathematics, Volume 125 (Cambridge Univ. Press, Cambridge, 2010).Google Scholar
Langlands, R., On Artin’s L-function, Rice Univ. Stud. 56(2) (1970), 23–28 Available at http://sunsite.ubc.ca/DigitalMathArchive/Langlands/JL.html.Google Scholar
Laumon, G., Transformations canoniques et spécialisation pour les D-modules filtrés, Astérisque 130 (1985), 56–129.Google Scholar
Laumon, G., Transformation de Fourier, constantes d’équations fonctionnelles et conjecture de Weil, Publ. Math. Inst. Hautes Études Sci. 65 (1987), 131–210.Google Scholar
Li, H. and van Oystaeyen, F., Zariskian Filtrations, K-Monographs in Math., Volume 2 (Kluwer, Dordrecht, 1996).Google Scholar
Lopez, R. G., Microlocalisation and stationary phase, Asian J. Math. 8(4) (2004), 747–768.Google Scholar
Malgrange, B., Équations Différentielles à Coefficients Polynomiaux. (Birkhäuser, Boston, 1991).Google Scholar
Marmora, A., Facteurs epsilon p-adiques, Compos. Math. 144 (2008), 439–483.CrossRefGoogle Scholar
Matsuda, S., Local indeces of p-adic differential operators corresponding to Artin–Schreier–Witt coverings, Duke Math. J. 77(3) (1995), 607–625.Google Scholar
Matsuda, S., Katz correspondence for quasi-unipotent overconvergent isocrystals, Compos. Math. 134 (2002), 1–34.Google Scholar
Mebkhout, Z., Analogue p-adique du théorème de Turrittin et le théorème de la monodromie p-adique, Invent. Math. 148 (2002), 319–351.Google Scholar
Mebkhout, Z. and Narvaez-Macarro, L., Sur les coefficients de de Rham–Grothendieck des variétés algébriques, Lecture Notes in Math., Volume 1454, pp. 267–308 (Springer-Verlag, Berlin, 1990).Google Scholar
Noot-Huyghe, C., Transformation de Fourier des D-modules arithmétiques I, in Geometric Aspects of Dwork Theory, Volume II, pp. 857–907 (Walter de Gruyter, 2004).Google Scholar
Noot-Huyghe, C., Comparison theorem between Fourier transform and Fourier transform with compact support, J. Théor. Nombres Bordeaux 25(1) (2013), 79–97.CrossRefGoogle Scholar
Petrequin, D., Classe de Chern en cohomologie rigide, Bull. Soc. Maths France 131(1) (2003), 59–121.Google Scholar
Pulita, A., Rank one solvable p-adic differential equations and finite Abelian characters via Lubin–Tate groups, Math. Ann. 337 (2007), 489–555.Google Scholar
Sabbah, C., Déformations isomonodromiques et variétés de Frobenius. (CNRS Ed., Paris, 2002).Google Scholar
Serre, J. -P., Corps Locaux, Deuxième Édition. (Hermann, Paris, 1968).Google Scholar
Schneider, P. and Teitelbaum, J., Algebras of p-adic distributions and admissible representations, Invent. Math. 153 (2003), 145–196.Google Scholar
van Tiel, J., Espaces localement K-convexes. II, Indag. Math. 27 (1965), 259–272.Google Scholar
Tsuzuki, N., Morphisms of F-isocrystals and the finite monodromy theorem for unit-root F-isocrystals, Duke Math. J. 111(3) (2002), 385–419.Google Scholar
Tsuzuki, N., Slope filtration of quasi-unipotent overconvergent F-isocrystals, Ann. Inst. Fourier 48 (1998), 379–412.Google Scholar
Tsuzuki, N., Finite local monodromy of overconvergent unit-root F-isocrystals on a curve, Am. J. Maths 120 (1998), 1165–1190.Google Scholar
Virrion, A., Dualité locale et holonomie pour les D-modules arithmétiques, Bull. Soc. Maths France 128 (2000), 1–68.Google Scholar