Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-22T16:43:56.767Z Has data issue: false hasContentIssue false
  • English
  • Français

PINNING ON A DEFECT LINE: CHARACTERIZATION OF MARGINAL DISORDER RELEVANCE AND SHARP ASYMPTOTICS FOR THE CRITICAL POINT SHIFT

Part of: Equilibrium statistical mechanics Special processes

Published online by Cambridge University Press:  29 January 2016

Quentin Berger  and
Hubert Lacoin
Quentin Berger
Affiliation:
LPMA, Université Pierre et Marie Curie, Campus Jussieu, case 188, 4 place Jussieu, 75252 Paris Cedex 5, France ([email protected])
Hubert Lacoin
Affiliation:
IMPA, Estrada Dona Castorina 110, Rio de Janeiro, 22460-320, Brasil ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

The effect of disorder for pinning models is a subject which has attracted much attention in theoretical physics and rigorous mathematical physics. A peculiar point of interest is the question of coincidence of the quenched and annealed critical point for a small amount of disorder. The question has been mathematically settled in most cases in the last few years, giving in particular a rigorous validation of the Harris criterion on disorder relevance. 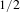However, the marginal case, where the return probability exponent is equal to $1/2$, that is, where the interarrival law of the renewal process is given by 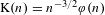$\text{K}(n)=n^{-3/2}\unicode[STIX]{x1D719}(n)$ where $\unicode[STIX]{x1D719}$ is a slowly varying function, has been left partially open. In this paper, we give a complete answer to the question by proving a simple necessary and sufficient criterion on the return probability for disorder relevance, which confirms earlier predictions from the literature. Moreover, we also provide sharp asymptotics on the critical point shift: in the case of the pinning of a one-dimensional simple random walk, the shift of the critical point satisfies the following high temperature asymptotics

$$\begin{eqnarray}\lim _{\unicode[STIX]{x1D6FD}\rightarrow 0}\unicode[STIX]{x1D6FD}^{2}\log h_{c}(\unicode[STIX]{x1D6FD})=-\frac{\unicode[STIX]{x1D70B}}{2}.\end{eqnarray}$$
This gives a rigorous proof to a claim of Derrida, Hakim and Vannimenus (J. Stat. Phys. 66 (1992), 1189–1213).

Keywords

Disordered pinning/wetting modellocalization transitiondisorder relevanceHarris criterion

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory 60K37: Processes in random environments 82B27: Critical phenomena 82B44: Disordered systems (random Ising models, random Schrödinger operators, etc.)
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 17 , Issue 2 , April 2018 , pp. 305 - 346
Copyright
© Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexander, K. S., The effect of disorder on polymer depinning transitions, Comm. Math. Phys. 279 (2008), 117–146.Google Scholar
Alexander, K. and Sidoravicius, V., Pinning of polymers and interfaces by random potentials, Ann. Appl. Probab. 16 (2006), 636–669.Google Scholar
Alexander, K. S. and Zygouras, N., Quenched and annealed critical points in polymer pinning models, Comm. Math. Phys. 291 (2009), 659–689.CrossRefGoogle Scholar
Alexander, K. S. and Zygouras, N., Equality of critical points for polymer depinning transitions with loop exponent one, Ann. Appl. Probab. 20 (2010), 356–366.Google Scholar
Alexander, K. S. and Zygouras, N., Path properties of the disordered pinning model in the delocalized regime, Ann. Appl. Probab. 24 (2014), 599–615.Google Scholar
Berger, Q., Pinning model in random correlated environment: appearance of an infinite disorder regime, J. Stat. Phys. 155 (2014), 544–570.CrossRefGoogle Scholar
Berger, Q., Caravenna, F., Poisat, J., Sun, R. and Zygouras, N., The critical curve of the random pinning and copolymer models at weak coupling, Comm. Math. Phys. 326 (2014), 507–530.Google Scholar
Berger, Q. and Lacoin, H., Sharp critical behavior for pinning models in a random correlated environment, Stochastic Process. Appl. 122 (2012), 1397–1436.Google Scholar
Berger, Q. and Lacoin, H., The high-temperature behavior for the directed polymer in dimension 1 + 2, Ann. Inst. Henri Poincaré Probab. Stat., to appear.Google Scholar
Berger, Q. and Toninelli, F. L., On the critical point of the random walk pinning model in dimension d = 3, Electron. J. Probab. 15 (2010), 654–683.Google Scholar
Bhattacharjee, S. M. and Mukherji, S., Directed polymers with random interaction - Marginal relevance and novel criticality, Phys. Rev. Lett. 70 (1993), 49–52.Google Scholar
Bhattacharjee, S. M. and Mukherji, S., Directed polymers with random interaction - An exactly solvable case, Phys. Rev. E 48 (1993), 3483–3496.Google Scholar
Bingham, N. H., Goldie, C. M. and Teugels, J. L., Regular Variations (Cambridge University Press, Cambridge, 1987).Google Scholar
Birkner, M. and Sun, R., Annealed vs quenched critical points for a random walk pinning model, Ann. Inst. Henri Poincaré Probab. Stat. 46 (2010), 414–441.Google Scholar
Birkner, M. and Sun, R., Disorder relevance for the random walk pinning model in dimension 3, Ann. Inst. Henri Poincaré Probab. Stat. 47 (2011), 259–293.Google Scholar
Bodineau, T., Giacomin, G., Lacoin, H. and Toninelli, F. L., Copolymers at selective interfaces: new bounds on the phase diagram, J. Stat. Phys. 132 (2008), 603–626.Google Scholar
Caravenna, F. and den Hollander, F., A general smoothing inequality for disordered polymers, Electron. Commun. Probab. 18(76) (2013), 1–15.CrossRefGoogle Scholar
Caravenna, F., Sun, R. and Zygouras, N., Polynomial chaos and scaling limits of disordered systems, J. Eur. Math. Soc., to appear.Google Scholar
Caravenna, F., Sun, R. and Zygouras, N., The continuum disordered pinning model, Probab. Theory Related Fields, to appear.Google Scholar
Caravenna, F., Sun, R. and Zygouras, N., Universality in marginally relevant disordered systems, Preprint, arXiv:1510.06287.Google Scholar
Caravenna, F., Toninelli, F. L. and Torri, N., Universality for the pinning model in the weak coupling regime, Preprint, arXiv:1505.04927.Google Scholar
Cheliotis, D. and den Hollander, F., Variational characterization of the critical curve for pinning of random polymers, Ann. Probab. 41 (2013), 1767–1805.Google Scholar
Cule, D. and Hwa, T., Denaturation of heterogeneous DNA, Phys. Rev. Lett. 79 (1997), 2375–2378.Google Scholar
Derrida, B., Hakim, V. and Vannimenus, J., Effect of disorder on two-dimensional wetting, J. Stat. Phys. 66 (1992), 1189–1213.Google Scholar
Derrida, B., Giacomin, G., Lacoin, H. and Toninelli, F. L., Fractional moment bounds and disorder relevance for pinning models, Comm. Math. Phys. 287 (2009), 867–887.Google Scholar
Derrida, B. and Retaux, M., The depinning transition in presence of disorder: a toy model, J. Stat. Phys. 156 (2014), 268–290.Google Scholar
Doney, R. A., One-sided local large deviation and renewal theorems in the case of infinite mean, Probab. Theory Related Fields 107 (1997), 451–465.Google Scholar
Fisher, M. E., Walks, walls, wetting, and melting, J. Stat. Phys. 34 (1984), 667–729.Google Scholar
Forgacs, G., Luck, J. M., Nieuwenhuizen, Th. M. and Orland, H., Wetting of a disordered substrate: exact critical behavior in two dimensions, Phys. Rev. Lett. 57 (1986), 2184–2187.Google Scholar
Gangardt, D. M. and Nechaev, S. K., Wetting transition on a one-dimensional disorder, J. Stat. Phys. 130 (2008), 483–502.Google Scholar
Giacomin, G., Random Polymer Models (Imperial College Press, World Scientific, London, 2007).Google Scholar
Giacomin, G., Disorder and critical phenomena through basic probability models, in École d’été de probablités de Saint-Flour XL-2010, Lecture Notes in Mathematics, Volume 2025 (Springer, Heidelberg, 2011).Google Scholar
Giacomin, G. and Lacoin, H., Pinning and disorder relevance for the discrete Gaussian free-field, Preprint, arXiv:1501.07909 [math.PR].Google Scholar
Giacomin, G., Lacoin, H. and Toninelli, F. L., Hierarchical pinning models, quadratic maps and quenched disorder, Probab. Theory Related Fields 147 (2010), 185–216.Google Scholar
Giacomin, G., Lacoin, H. and Toninelli, F. L., Marginal relevance of disorder for pinning models, Comm. Pure Appl. Math. 63 (2010), 233–265.Google Scholar
Giacomin, G., Lacoin, H. and Toninelli, F. L., Disorder relevance at marginality and critical point shift, Ann. Inst. Henri Poincaré Probab. Stat. 47 (2011), 148–175.Google Scholar
Giacomin, G. and Toninelli, F. L., Smoothing effect of quenched disorder on polymer depinning transitions, Comm. Math. Phys. 266 (2006), 1–16.Google Scholar
Giacomin, G. and Toninelli, F. L., On the irrelevant disorder regime of pinning models, Ann. Probab. 37 (2009), 1841–1875.Google Scholar
Harris, A. B., Effect of random defects on the critical behaviour of Ising models, J. Phys. C 7 (1974), 1671–1692.CrossRefGoogle Scholar
Kafri, Y. and Mukamel, D., Griffiths singularities in unbinding of strongly disordered polymers, Phys. Rev. Lett. 91 (2003), 038103.Google Scholar
Kunz, H. and Livi, R., DNA denaturation and wetting in the presence of disorder, Eur. Phys. Lett. 99 (2012), 30001.Google Scholar
Lacoin, H., Hierarchical pinning model with site disorder: disorder is marginally relevant, Probab. Theory Related Fields 148 (2010), 159–175.Google Scholar
Lacoin, H., New bounds for the free energy of directed polymers in dimension 1 + 1 and 1 + 2, Comm. Math. Phys. 294 (2010), 471–503.CrossRefGoogle Scholar
Lacoin, H., The martingale approach to disorder irrelevance for pinning models, Electron. Commun. Probab. 15 (2010), 418–427.Google Scholar
Lacoin, H., Non-coincidence of quenched and annealed connective constants on the supercritical planar percolation cluster, Probab. Theory Related Fields 159 (2014), 777–808.Google Scholar
Lacoin, H., The rounding of the phase transition for disordered pinning with stretched exponential tails, Preprint, arXiv:1405.6875 [math-ph].Google Scholar
Lacoin, H., Pinning and disorder relevance for the discrete Gaussian free-field II: the two dimensional case, Preprint, arXiv:1512.05240 [math.PR].Google Scholar
Monthus, C., Random walks and polymers in the presence of quenched disorder, Lett. Math. Phys. 78 (2006), 207–233.Google Scholar
Monthus, C. and Garel, T., Multifractal statistics of the local order parameter at random critical points: application to wetting transitions with disorder, Phys. Rev. E 76 (2007), 021114.CrossRefGoogle ScholarPubMed
Nakashima, M., A remark on the bound for the free energy of directed polymers in random environment in 1 + 2 dimension, J. Math. Phys. 55 (2014), 093304.Google Scholar
Poisat, J., Random pinning model with finite range correlations: disorder relevant regime, Stochastic Process. Appl. 122 (2012), 3560–3579.Google Scholar
Tang, L. H. and Chaté, H., Rare-event induced binding transition of heteropolymers, Phys. Rev. Lett. 86 (2001), 830–833.Google Scholar
Toninelli, F. L., A replica-coupling approach to disordered pinning models, Comm. Math. Phys. 280 (2008), 389–401.Google Scholar
Toninelli, F. L., Disordered pinning models and copolymers: beyond annealed bounds, Ann. Appl. Probab. 18 (2008), 1569–1587.Google Scholar
Zygouras, N., Strong disorder in semidirected random polymers, Ann. Inst. Henri Poincaré Probab. Stat. 49 (2013), 753–780.Google Scholar
Yilmaz, A. and Zeitouni, O., Differing averaged and quenched large deviations for random walks in random environments in dimensions two and three, Comm. Math. Phys. 300 (2010), 243–271.Google Scholar