Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T01:23:17.108Z Has data issue: false hasContentIssue false
  • English
  • Français

ORBIFOLD POINTS ON PRYM–TEICHMÜLLER CURVES IN GENUS $4$

Part of: Differential topology Special properties Curves

Published online by Cambridge University Press:  22 May 2017

David Torres-Teigell  and
Jonathan Zachhuber
David Torres-Teigell
Affiliation:
Fachrichtung Mathematik, Universität des Saarlandes, Campus E24, 66123 Saarbrücken, Germany ([email protected])
Jonathan Zachhuber
Affiliation:
FB 12 – Institut für Mathematik, Johann Wolfgang Goethe-Universität, Robert-Mayer-Str. 6–8, D-60325 Frankfurt am Main, Germany ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

For each discriminant 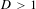$D>1$, McMullen constructed the Prym–Teichmüller curves 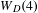$W_{D}(4)$ and 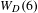$W_{D}(6)$ in 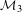${\mathcal{M}}_{3}$ and 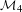${\mathcal{M}}_{4}$, which constitute one of the few known infinite families of geometrically primitive Teichmüller curves. In the present paper, we determine for each 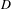$D$ the number and type of orbifold points on 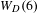$W_{D}(6)$. These results, together with a previous result of the two authors in the genus $3$ case and with results of Lanneau–Nguyen and Möller, complete the topological characterisation of all Prym–Teichmüller curves and determine their genus. The study of orbifold points relies on the analysis of intersections of 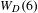$W_{D}(6)$ with certain families of genus $4$ curves with extra automorphisms. As a side product of this study, we give an explicit construction of such families and describe their Prym–Torelli images, which turn out to be isomorphic to certain products of elliptic curves. We also give a geometric description of the flat surfaces associated to these families and describe the asymptotics of the genus of 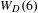$W_{D}(6)$ for large 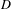$D$.

Keywords

flat surfacesTeichmüller curvesorbifold pointscyclic covers

MSC classification

Primary: 14H10: Families, moduli (algebraic)
Secondary: 14H40: Jacobians, Prym varieties 14H52: Elliptic curves 57R18: Topology and geometry of orbifolds 54F65: Topological characterizations of particular spaces
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 18 , Issue 4 , July 2019 , pp. 673 - 706
Copyright
© Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bainbridge, M., Euler characteristics of Teichmüller curves in genus two, Geom. Topol. 11 (2007), 1887–2073.Google Scholar
Bainbridge, M., Chen, D., Gendron, Q., Grushevsky, S. and Möller, M., Strata of $k$ -Differentials, Preprint, 2016, arXiv:1610.09238 [math.AG].Google Scholar
Birkenhake, C. and Lange, H., Complex Abelian Varieties, Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen, (Springer, Berlin, 2004).Google Scholar
Bouw, I., Pseudo-elliptic bundles, deformation data, and the reduction of Galois covers, Habilitation, Universität Duisburg–Essen, 2005. URL: http://www.mathematik.uni-ulm.de/ReineMath/mitarbeiter/bouw/papers/crystal.ps.Google Scholar
Broughton, S. A., Classifying finite group actions on surfaces of low genus, J. Pure Appl. Algebra 69(3) (1991), 233–270.Google Scholar
Bujalance, E. and Conder, M., On cyclic groups of automorphisms of Riemann surfaces, J. Lond. Math. Soc. (2) 59(2) (1999), 573–584.Google Scholar
Cohen, H., A Course in Computational Algebraic Number Theory, Graduate Texts in Mathematics, Volume 138 (Springer, Berlin, 1993).Google Scholar
González-Diez, G. and Harvey, W. J., Moduli of Riemann surfaces with symmetry, in Discrete Groups and Geometry (Birmingham, 1991), (ed. Harvey, W. J. and Maclachlan, C.), London Mathematical Society Lecture Note Series, Volume 173, pp. 175–193 (Cambridge University Press, Cambridge, 1992).Google Scholar
Lanneau, E. and Nguyen, D.-M., Teichmüller curves generated by Weierstrass Prym eigenforms in genus 3 and genus 4, J. Topol. 7(2) (2014), 475–522.Google Scholar
Lanneau, E. and Nguyen, D.-M., Teichmüller curves and Weierstrass Prym eigenforms in genus four, in preparation, 2016.Google Scholar
Lehman, J. L., Levels of positive definite ternary quadratic forms, Math. Comp. 58(197) (1992), 399–417.Google Scholar
McMullen, C. T., Billiards and Teichmüller curves on Hilbert modular surfaces, J. Amer. Math. Soc. 16(4) (2003), 857–885.Google Scholar
McMullen, C. T., Teichmüller curves in genus two: discriminant and spin, Math. Ann. 333(1) (2005), 87–130.Google Scholar
McMullen, C. T., Prym varieties and Teichmüller curves, Duke Math. J. 133(3) (2006), 569–590.Google Scholar
McMullen, C. T., Mukamel, R. E. and Wright, A., Cubic curves and totally geodesic subvarieties of moduli space, Ann. of Math. (2) 185(3) (2017), 957–990.Google Scholar
Möller, M., Teichmüller Curves, Mainly from the Viewpoint of Algebraic Geometry, IAS/Park City Mathematics Series, (2011).Google Scholar
Möller, M., Prym covers, theta functions and Kobayashi geodesics in Hilbert modular surfaces, Amer. J. Math. 135 (2014), 995–1022.Google Scholar
Möller, M. and Zagier, D., Modular embeddings of Teichmüller curves, Compos. Math. 152 (2016), 2269–2349.Google Scholar
Mukamel, R. E., Orbifold points on Teichmüller curves and Jacobians with complex multiplication, Geom. Topol. 18(2) (2014), 779–829.Google Scholar
PARI/GP version 2.3.5 The PARI Group. Bordeaux, 2010, URL: http://pari.math.u-bordeaux.fr/.Google Scholar
Rohde, J. C., Cyclic Coverings, Calabi-Yau Manifolds and Complex Multiplication, Lecture Notes in Mathematics, Volume Nr. 1975 (Springer, Berlin, 2009).Google Scholar
Schiller, J., Moduli for special Riemann surfaces of genus 2, Trans. Amer. Math. Soc. 144 (1969), 95–113.Google Scholar
Shimura, G., On modular forms of half-integral weight, Ann. of Math. (2) 97(2) (1973), 440–481.Google Scholar
Singerman, D., Finitely maximal Fuchsian groups, J. Lond. Math. Soc. (2) 6 (1972), 29–38.Google Scholar
Torres-Teigell, D. and Zachhuber, J., Orbifold points on Prym–Teichmüller curves in genus three, Int. Math. Res. Not. IMRN (2016), doi:10.1093/imrn/rnw277, to appear.Google Scholar
Zachhuber, J., The Galois action and a spin invariant for Prym–Teichmüller curves in genus 3, Bull. Soc. Math. France (2016), to appear.Google Scholar