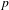Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-05T11:54:40.432Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE $p$-ADIC VARIATION OF HEEGNER POINTS

Part of: Arithmetic algebraic geometry

Published online by Cambridge University Press:  18 February 2019

Francesc Castella
Francesc Castella*
Affiliation:
Mathematics Department, Princeton University, Fine Hall, Princeton, NJ 08544-1000, USA ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we prove an ‘explicit reciprocity law’ relating Howard’s system of big Heegner points to a two-variable 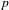$p$-adic $L$-function (constructed here) interpolating the 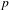$p$-adic Rankin $L$-series of Bertolini–Darmon–Prasanna in Hida families. As applications, we obtain a direct relation between classical Heegner cycles and the higher weight specializations of big Heegner points, refining earlier work of the author, and prove the vanishing of Selmer groups of CM elliptic curves twisted by 2-dimensional Artin representations in cases predicted by the equivariant Birch and Swinnerton-Dyer conjecture.

Keywords

Heegner pointsHida familiesp-adic L-functionsequivariant Birch–Swinnerton-Dyer conjecture

MSC classification

Primary: 11G05: Elliptic curves over global fields
Secondary: 11G40: $L$-functions of varieties over global fields; Birch-Swinnerton-Dyer conjecture
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 6 , November 2020 , pp. 2127 - 2164
Check for updates
Copyright
© Cambridge University Press 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author was supported in part by NSF grant DMS-1801385. This project received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 682152).

References

Bellaïche, J. and Dimitrov, M., On the eigencurve at classical weight 1 points, Duke Math. J. 165(2) (2016), 245–266; MR 3457673.Google Scholar
Berger, L., Bloch and Kato’s exponential map: three explicit formulas, Doc. Math. (2003), no. Extra vol., 99–129 (electronic), Kazuya Kato’s fiftieth birthday; MR 2046596 (2005f:11268).Google Scholar
Bertolini, M., Darmon, H. and Prasanna, K., Generalized Heegner cycles and p-adic Rankin L-series, Duke Math. J. 162(6) (2013), 1033–1148; MR 3053566.Google Scholar
Bertolini, M., Darmon, H. and Prasanna, K., p-adic L-functions and the coniveau filtration on Chow groups, J. Reine Angew. Math. 731 (2017), 21–86. With an appendix by Brian Conrad; MR 3709060.Google Scholar
Bertolini, M., Darmon, H. and Rotger, V., Beilinson–Flach elements and Euler systems II: the Birch–Swinnerton-Dyer conjecture for Hasse–Weil–Artin L-series, J. Algebraic Geom. 24(3) (2015), 569–604; MR 3344765.Google Scholar
Bloch, S. and Kato, K., L-functions and Tamagawa numbers of motives, in The Grothendieck Festschrift, Vol. I, Progress in Mathematics, Volume 86, pp. 333–400 (Birkhä user Boston, Boston, MA, 1990); MR 1086888 (92g:11063).Google Scholar
Brakočević, M., Anticyclotomic p-adic L-function of central critical Rankin–Selberg L-value, Int. Math. Res. Not. IMRN 21 (2011), 4967–5018; MR 2852303.Google Scholar
Brakočević, M., Two variable anticyclotomic $p$-adic $L$-functions for Hida families, Preprint, 2012, arXiv:1203.0953.Google Scholar
Büyükboduk, K., Big Heegner point Kolyvagin system for a family of modular forms, Selecta Math. (N.S.) 20(3) (2014), 787–815; MR 3217460.Google Scholar
Castella, F., Heegner cycles and higher weight specializations of big Heegner points, Math. Ann. 356(4) (2013), 1247–1282; MR 3072800.Google Scholar
Castella, F., On the exceptional specializations of big Heegner points, J. Inst. Math. Jussieu 17(1) (2018), 207–240; MR 3742560.Google Scholar
Castella, F. and Hsieh, M.-L., Heegner cycles and p-adic L-functions, Math. Ann. 370(1–2) (2018), 567–628; MR 3747496.Google Scholar
Hecke, E., Zur Theorie der elliptischen Modulfunktionen, Math. Ann. 97(1) (1927), 210–242; MR 1512360.Google Scholar
Hida, H., Galois representations into GL2(Zp[[X]]) attached to ordinary cusp forms, Invent. Math. 85(3) (1986), 545–613; MR 848685 (87k:11049).Google Scholar
Hida, H., Iwasawa modules attached to congruences of cusp forms, Ann. Sci. Éc. Norm. Supér. (4) 19(2) (1986), 231–273; MR 868300 (88i:11023).Google Scholar
Hida, H., Geometric Modular Forms and Elliptic Curves (World Scientific Publishing Co., Inc., River Edge, NJ, 2000); MR 1794402 (2001j:11022).Google Scholar
Howard, B., The Heegner point Kolyvagin system, Compos. Math. 140(6) (2004), 1439–1472; MR 2098397 (2006a:11070).Google Scholar
Howard, B., Central derivatives of L-functions in Hida families, Math. Ann. 339(4) (2007), 803–818; MR 2341902 (2008m:11125).Google Scholar
Howard, B., Variation of Heegner points in Hida families, Invent. Math. 167(1) (2007), 91–128; MR 2264805 (2007h:11067).Google Scholar
Hsieh, M.-L., Special values of anticyclotomic Rankin–Selberg L-functions, Doc. Math. 19 (2014), 709–767; MR 3247801.Google Scholar
Kings, G., Loeffler, D. and Zerbes, S. L., Rankin–Eisenstein classes and explicit reciprocity laws, Camb. J. Math. 5(1) (2017), 1–122; MR 3637653.Google Scholar
Khare, C. and Wintenberger, J.-P., Serre’s modularity conjecture. I, Invent. Math. 178(3) (2009), 485–504; MR 2551763.Google Scholar
Loeffler, D. and Zerbes, S. L., Iwasawa theory and p-adic L-functions over ℤp2 -extensions, Int. J. Number Theory 10(8) (2014), 2045–2095; MR 3273476.Google Scholar
Mazur, B. and Tilouine, J., Représentations galoisiennes, différentielles de Kähler et ‘conjectures principales’, Publ. Math. Inst. Hautes Études Sci. 71 (1990), 65–103; MR 1079644 (92e:11060).10.1007/BF02699878Google Scholar
Nekovář, J., On the p-adic height of Heegner cycles, Math. Ann. 302(4) (1995), 609–686; MR 1343644 (96f:11073).Google Scholar
Nekovář, J., p-adic Abel–Jacobi maps and p-adic heights, in The Arithmetic and Geometry of Algebraic Cycles (Banff, AB 1998), CRM Proceedings Lecture Notes, Volume 24, pp. 367–379 (American Mathematical Society, Providence, RI, 2000); MR 1738867 (2002e:14011).Google Scholar
Ochiai, T., A generalization of the Coleman map for Hida deformations, Amer. J. Math. 125(4) (2003), 849–892; MR 1993743 (2004j:11050).Google Scholar
Perrin-Riou, B., Théorie d’Iwasawa des représentations p-adiques sur un corps local, Invent. Math. 115(1) (1994), 81–161. With an appendix by Jean-Marc Fontaine; MR 1248080 (95c:11082).Google Scholar
Perrin-Riou, B., p-Adic L-Functions and p-Adic Representations, SMF/AMS Texts and Monographs, Volume 3, (American Mathematical Society, Providence, RI, 2000). Translated from the 1995 French original by Leila Schneps and revised by the author.Google Scholar
Shnidman, A., p-adic heights of generalized Heegner cycles, Ann. Inst. Fourier (Grenoble) 66(3) (2016), 1117–1174; MR 3494168.Google Scholar
Wiles, A., On ordinary 𝜆-adic representations associated to modular forms, Invent. Math. 94(3) (1988), 529–573; MR 969243 (89j:11051).Google Scholar