Published online by Cambridge University Press: 01 December 2023
We study conjugacy classes of germs of nonflat diffeomorphisms of the real line fixing the origin. Based on the work of Takens and Yoccoz, we establish results that are sharp in terms of differentiability classes and order of tangency to the identity. The core of all of this lies in the invariance of residues under low-regular conjugacies. This may be seen as an extension of the fact (also proved in this article) that the value of the Schwarzian derivative at the origin for germs of 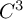 $C^3$ parabolic diffeomorphisms is invariant under
$C^3$ parabolic diffeomorphisms is invariant under 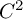 $C^2$ parabolic conjugacy, though it may vary arbitrarily under parabolic
$C^2$ parabolic conjugacy, though it may vary arbitrarily under parabolic 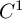 $C^1$ conjugacy.
$C^1$ conjugacy.