Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Mallory, Devlin
2021.
Bigness of the tangent bundle of del Pezzo
surfaces and D-simplicity.
Algebra & Number Theory,
Vol. 15,
Issue. 8,
p.
2019.
Höring, Andreas
Liu, Jie
and
Shao, Feng
2022.
Examples of Fano manifolds with non‐pseudoeffective tangent bundle.
Journal of the London Mathematical Society,
Vol. 106,
Issue. 1,
p.
27.
Matsumura, Shin-ichi
2022.
Open problems on structure of positively curved projective varieties.
Annales de la Faculté des sciences de Toulouse : Mathématiques,
Vol. 31,
Issue. 3,
p.
1011.
Wang, Juanyong
2022.
Structure of projective varieties with nef anticanonical divisor: the case of log terminal singularities.
Mathematische Annalen,
Vol. 384,
Issue. 1-2,
p.
1.
Ohsawa, Takeo
2023.
Miscellanea on PSH Functions and $$L^2$$ Methods on Pseudoconvex Domains.
The Journal of Geometric Analysis,
Vol. 33,
Issue. 10,
Ejiri, Sho
Iwai, Masataka
and
Matsumura, Shin-ichi
2023.
On asymptotic base loci of relative anti-canonical divisors of algebraic fiber spaces.
Journal of Algebraic Geometry,
Vol. 32,
Issue. 3,
p.
477.
Chen, Yong
and
Zhang, Xi
2023.
Pseudo-Effective Vector Bundles with Vanishing First Chern Class on Astheno-Kähler Manifolds.
Chinese Annals of Mathematics, Series B,
Vol. 44,
Issue. 6,
p.
819.
OHSAWA, TAKEO
2023.
ON HYPERCONVEXITY AND TOWARDS BUNDLE-VALUED KERNEL ASYMPTOTICS ON LOCALLY PSEUDOCONVEX DOMAINS.
Revue Roumaine Mathematiques Pures Appliquees,
Vol. LXVIII,
Issue. 1-2,
p.
169.
Höring, Andreas
and
Liu, Jie
2023.
Fano manifolds with big tangent bundle: a characterisation of $$V_5$$.
Collectanea Mathematica,
Vol. 74,
Issue. 3,
p.
639.
Lombardi, Luigi
and
Schnell, Christian
2023.
Singular hermitian metrics and the decomposition theorem of Catanese, Fujita, and Kawamata.
Proceedings of the American Mathematical Society,
Vol. 152,
Issue. 1,
p.
137.
Ejiri, Sho
Fujino, Osamu
and
Iwai, Masataka
2024.
Positivity of extensions of vector bundles.
Mathematische Zeitschrift,
Vol. 306,
Issue. 3,
Müller, Niklas
2025.
Locally constant fibrations and positivity of curvature.
Bulletin of the London Mathematical Society,
Iwai, Masataka
2025.
On the structure of a log smooth pair in the equality case of the Bogomolov–Gieseker inequality.
Annales de l'Institut Fourier,
Vol. 75,
Issue. 1,
p.
49.
JIA, Jia
LEE, Yongnam
and
ZHONG, Guolei
2025.
Smooth projective surfaces with pseudo-effective tangent bundles.
Journal of the Mathematical Society of Japan,
Vol. 77,
Issue. 1,
Matsumura, Shin-ichi
2025.
Complex Geometric Analysis.
Vol. 481,
Issue. ,
p.
137.
Matsumura, Shin-ichi
and
Wu, Xiaojun
2025.
Compact Kähler three-folds with nef anti-canonical bundle.
Mathematische Annalen,
Vol. 391,
Issue. 1,
p.
1253.
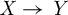 $X \to Y$
to a flat projective manifold Y such that its general fibre is rationally connected. Moreover, by applying this structure theorem, we classify all the minimal surfaces with pseudo-effective tangent bundle and study general nonminimal surfaces, which provide examples of (possibly singular) positively curved tangent bundles.
$X \to Y$
to a flat projective manifold Y such that its general fibre is rationally connected. Moreover, by applying this structure theorem, we classify all the minimal surfaces with pseudo-effective tangent bundle and study general nonminimal surfaces, which provide examples of (possibly singular) positively curved tangent bundles.