Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-23T01:47:07.373Z Has data issue: false hasContentIssue false
  • English
  • Français

On Mordell–Weil groups of Jacobians over function fields

Published online by Cambridge University Press:  15 May 2012

Douglas Ulmer
Douglas Ulmer*
Affiliation:
School of Mathematics, Georgia Institute of Technology, Atlanta, GA 30332, USA([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

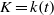We study the arithmetic of abelian varieties over where 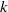is an arbitrary field. The main result relates Mordell–Weil groups of certain Jacobians over 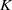to homomorphisms of other Jacobians over 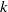. Our methods also yield completely explicit points on elliptic curves with unbounded rank over 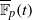and a new construction of elliptic curves with moderately high rank over .

Keywords

abelian variety; Jacobian; Mordell–Weil group; function field; rank14G0511G4011G0511G1011G3014G1014G2514K15
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 12 , Issue 1 , January 2013 , pp. 1 - 29
Copyright
Copyright © Cambridge University Press 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Barth, W. P., Hulek, K., Peters, C. A. M. and Van de Ven, A. , Compact complex surfaces, 2nd ed., Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge, Volume 4 (Springer-Verlag, Berlin, 2004).CrossRefGoogle Scholar
2.Beauville, A. , Complex algebraic surfaces, London Mathematical Society Lecture Note Series, Volume 68 (Cambridge University Press, Cambridge, 1983).Google Scholar
3.Berger, L. , Towers of surfaces dominated by products of curves and elliptic curves of large rank over function fields, J. Number Theory 128 (2008), 3013–3030.Google Scholar
4.Conceição, R. , PhD thesis, University of Texas (2009).Google Scholar
5.Conrad, B. , Chow’s -image and -trace, and the Lang–Néron theorem, Enseign. Math. (2) 52 (2006), 37–108.Google Scholar
6.Conway, J. H. and Sloane, N. J. A. , Sphere packings, lattices and groups, 3rd ed., Grundlehren der Mathematischen Wissenschaften, Volume 290 (Springer-Verlag, New York, 1999).Google Scholar
7.de Jong, J. and Noot, R. , Jacobians with complex multiplication, in Arithmetic algebraic geometry, Texel, 1989, Progr. Math., Volume 89, pp. 177–192 (Birkhäuser Boston, Boston, MA, 1991).Google Scholar
8.de Jong, J. , Variation of Hodge Structures: some examples, 2002, Lectures at the Arizona Winter School 2002 (Notes available at http://swc.math.arizona.edu).Google Scholar
9.de Jong, J. , Shioda cycles in families of surfaces, preprint (available at the author’s web site http://math.columbia.edu/~dejong, 2009).Google Scholar
10.Deligne, P. , La conjecture de Weil pour les surfaces , Invent. Math. 15 (1972), 206–226.CrossRefGoogle Scholar
11.Desrousseaux, P.-A. , Fonctions hypergéométriques de Lauricella, périodes de variétés abéliennes et transcendance, C. R. Math. Acad. Sci. Soc. R. Can. 26 (2004), 110–117.Google Scholar
12.Faltings, G. , Endlichkeitssätze für abelsche Varietäten über Zahlkörpern, Invent. Math. 73 (1983), 349–366.CrossRefGoogle Scholar
13.Liu, Q. , Algebraic geometry and arithmetic curves, Oxford Graduate Texts in Mathematics, Volume 6 (Oxford University Press, Oxford, 2002).CrossRefGoogle Scholar
14.Milne, J. S. , Jacobian varieties, in Arithmetic geometry, Storrs, Conn., 1984, pp. 167–212 (Springer, New York, 1986).Google Scholar
15.Occhipinti, T. , PhD thesis, University of Arizona (2010).Google Scholar
16.Raynaud, M. , Spécialisation du foncteur de Picard, Publ. Math. Inst. Hautes Études Sci. 38 (1970), 27–76.Google Scholar
17.Schoen, C. , Varieties dominated by product varieties, Internat. J. Math. 7 (1996), 541–571.Google Scholar
18.Shioda, T. , An explicit algorithm for computing the Picard number of certain algebraic surfaces, Amer. J. Math. 108 (1986), 415–432.CrossRefGoogle Scholar
19.Shioda, T. , Mordell–Weil lattices and sphere packings, Amer. J. Math. 113 (1991), 931–948.Google Scholar
20.Shioda, T. , Mordell–Weil lattices for higher genus fibration over a curve, in New trends in algebraic geometry, Warwick, 1996, London Math. Soc. Lecture Note Ser., Volume 264, pp. 359–373 (Cambridge Univ. Press, Cambridge, 1999).Google Scholar
21.Tate, J. , Endomorphisms of abelian varieties over finite fields, Invent. Math. 2 (1966), 134–144.Google Scholar
22.Tate, J. , On the conjectures of Birch and Swinnerton-Dyer and a geometric analog, Séminaire Bourbaki, Volume 9. pp. 415–440 (Soc. Math, France, Paris, 1995), Exp. No. 306.Google Scholar
23.Tate, J. , Conjectures on algebraic cycles in -adic cohomology, in Motives, Seattle, WA, 1991, Proc. Sympos. Pure Math., Volume 55, pp. 71–83 (Amer. Math. Soc., Providence, RI, 1994).Google Scholar
24.Ulmer, D. , -functions with large analytic rank and abelian varieties with large algebraic rank over function fields, Invent. Math. 167 (2007), 379–408.Google Scholar
25.Zarhin, Ju. G. , A finiteness theorem for isogenies of abelian varieties over function fields of finite characteristic, Funktsional. Anal. i Prilozhen. 8 (1974), 31–34.Google Scholar